0 引言
固井是油气井工程重要的工艺措施,是油气井建井过程中的关键环节[1]。现在国内有一种新的固井技术,该固井技术借鉴了建筑业水泥振荡器(混凝土振捣器)的工作原理,研制出了套管振荡器,通过套管振荡器对套管的周期性冲击,引起套管振动,将套管和井壁之间的水泥浆进行捣固,增强水泥界面的胶结强度,缩减水泥浆的胶凝时间,使水泥浆和套管及地层密实结合,消除水泥浆的蜂窝麻面等现象,达到提高固井质量的目的[2]。
套管振荡器在振动固井[3]过程中会对套管产生周期性冲击,可能会引起套管损坏。根据前人的研究可知,螺纹连接强度是套管承载能力的一个最重要技术指标,接头螺纹连接处的承载能力一般只有管体的70%左右[4],由此可知,螺连连接是套管柱中最薄弱的环节。调查发现,80%的套管失效发生在套管螺纹的连接处[5]。因此研究套管振荡器对套管冲击损坏主要集中在螺纹连接部分。
目前套管螺纹连接的应力研究主要集中在二维的有限元数值分析方面[6],受载条件也很简单(仅是单纯的上扣扭矩、拉伸载荷和内压,未考虑摩擦和弯矩等载荷的影响),对各种复合载荷联合作用的研究较少[7-8],而对于冲击载荷作用下的套管螺纹应力分析也未见公开报道,因此尚需进一步对冲击载荷作用下的套管螺纹连接应力场进行研究。笔者以API ϕ139.7 mm×7.72 mm N80钢级的圆锥套管圆螺纹为例,利用ANSYS软件[8]分析了套管螺纹连接部分的应力强度和在冲击载荷作用下螺纹连接部分的应力分布规律。所得结论可为有冲击载荷作用的振动固井技术提供理论支持。
1 有限元模型的建立以API ϕ139.7 mm×7.72 mm N80钢级的圆锥套管为研究对象,通过查阅API SPEC5B-2008CN[9]标准,计算得到螺纹机紧旋合和螺纹牙的几何尺寸如图 1和图 2所示。套管材料弹性模量210 GPa,泊松比0.3,密度7 850 kg/m3,屈服强度552~758 MPa。
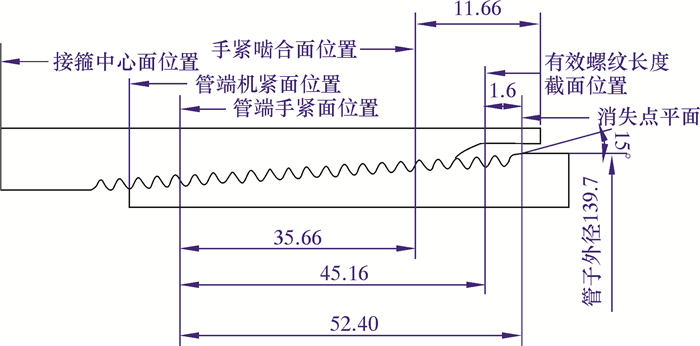
|
| 图 1 API圆螺纹机紧旋合几何尺寸 Fig.1 API round thread machine tight rotation dimension |
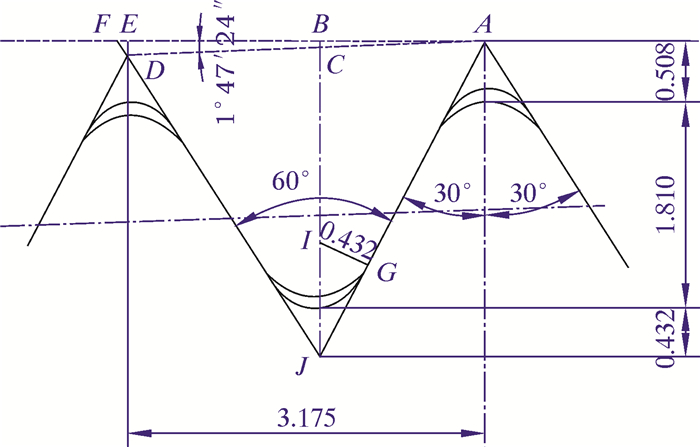
|
| 图 2 API螺纹牙几何尺寸 Fig.2 API thread dimension |
根据套管接头的结构和受力特点,在有限元建模时引入以下简化和假设[10]:① 忽略螺旋升角的影响,采用轴对称结构;② 接触面之间的摩擦因数与采用的螺纹脂有关,一般在0.015~0.025[11]之间,本次计算假定摩擦因数为0.02;③ 为了消除力学模型中边界效应的影响,模型两端延长螺纹长度的
考虑到在ANSYS中进行实体建模时无法模拟一些复杂零件的重要细节,而且建模的工作量很大,因此选择在CAD中建模,存成SAT文件格式,导入到ANSYS中进行有限元分析。图 3a所示即为导入到ANSYS中的有限元模型。模型选用PLANE183单元(高阶二维8节点),智能网格划分,由于在螺纹啮合部分可能会出现应力集中现象,所以对这些部位进行局部网格细化,划分后的网格如图 3b所示。图 3c为螺纹放大图。套管上剖分[12]的单元数为9 434个,节点数为20 935个,接箍上的单元数为9 775个,节点数为21 614个。
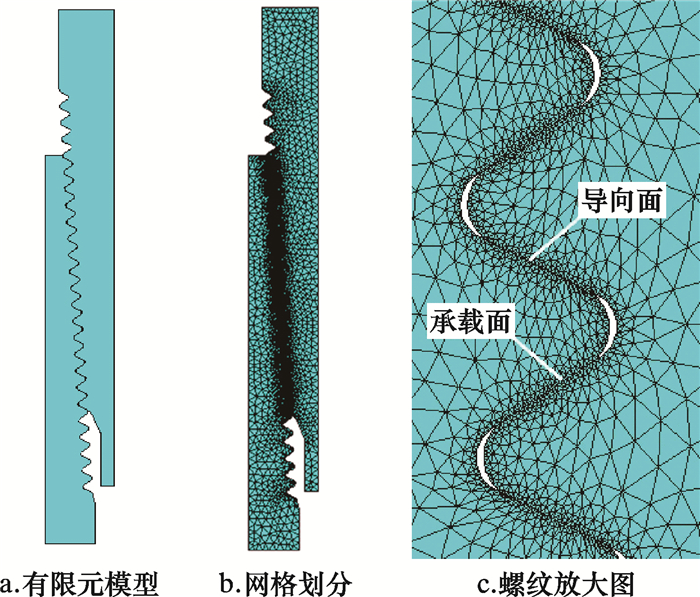
|
| 图 3 套管螺纹连接有限元模型 Fig.3 Finite element model of casing thread connection |
在上扣模拟过程中,套管螺纹连接扭矩的施加主要通过改变内、外螺纹之间的过盈量来实现。对于8牙API套管圆螺纹连接每机紧1圈,内、外螺纹牙之间产生的径向过盈量为0.099 mm[13]。螺纹牙径向过盈量的加载需要借助接触单元来实现,在分析过程中指定目标面和接触面,以及设置实常数和单元关键字来生成所需要的接触单元[14]。
在套管有限元模型中,对接箍上端施加位移固定约束,而套管接头所承受的载荷除了机紧上扣产生的过盈装配外,还有轴向拉伸、管内均布压力及其复合作用。为了便于计算和结果的比较,需要对螺纹各扣牙进行编号,左侧套管为外螺纹,外螺纹顶端螺纹牙设定为第1扣,在机紧1圈的工况环境下,从上到下依次进行编号共有16扣。笔者研究的是套管螺纹连接在不同载荷工况下的力学性能和在冲击载荷下的应力分布规律。
2 不同载荷下套管螺纹连接分析 2.1 机紧不同圈数的套管螺纹连接的应力分布在实际工况中API套管螺纹接头使用时需要合理的上扣位置(圈数),一般通过施加一定的扭矩来实现,API ϕ139.7 mm×7.72 mm套管在使用时要求有3扣的机紧圈数。图 4即显示出套管接头在机紧3圈的过程中螺纹连接Von Mises应力场的变化情况。由图可知,套管和接箍的应力在机紧3圈的过程中变化幅度不大,套管的应力水平整体上要高于接箍;并且套管和接箍螺纹首、末起始扣处的Von Mises应力均为各自管体的最大应力,机紧3圈工况下接箍内螺纹小端啮合螺纹第1扣的Von Mises应力值最大,最大值为2.26 MPa。
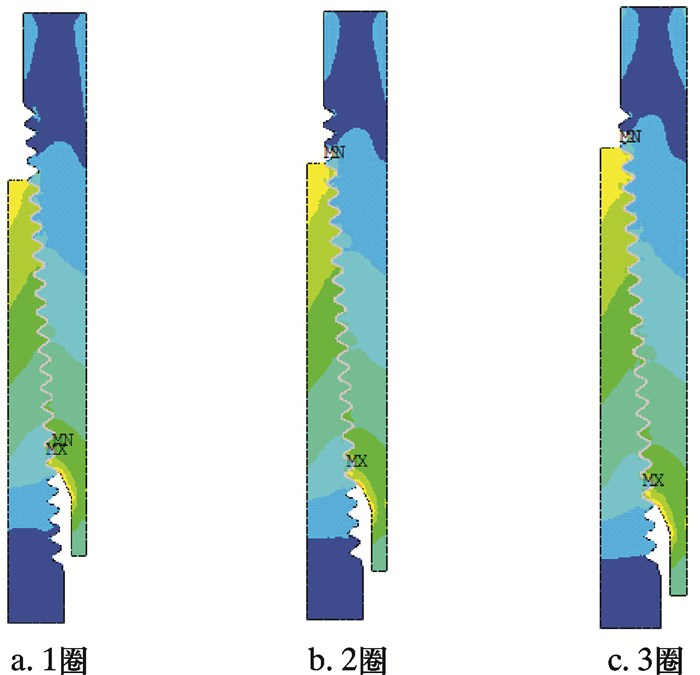
|
| 图 4 上扣过程中套管螺纹Von Mises应力的分布云图 Fig.4 Von Mises stress distribution of casing thread in the process of makeup |
图 5为套管内壁和接箍外壁在机紧3圈后其等效弹性应变沿轴向的分布情况。由图可知,套管和接箍均在小端螺纹起始扣处等效应变最大,然后沿着轴向距离应变逐渐减小。在套管螺纹起始扣处相对应的套管内壁产生的最大等效应变为8.18×10-6,与接箍起始扣相对应的接箍外壁,其最大等效应变为6.13×10-6。图 5b的曲线首尾各有一段和整体趋势不一样的变化曲线,这是因为接箍模型两端在螺纹啮合部位以外各有一段不受力的管体。
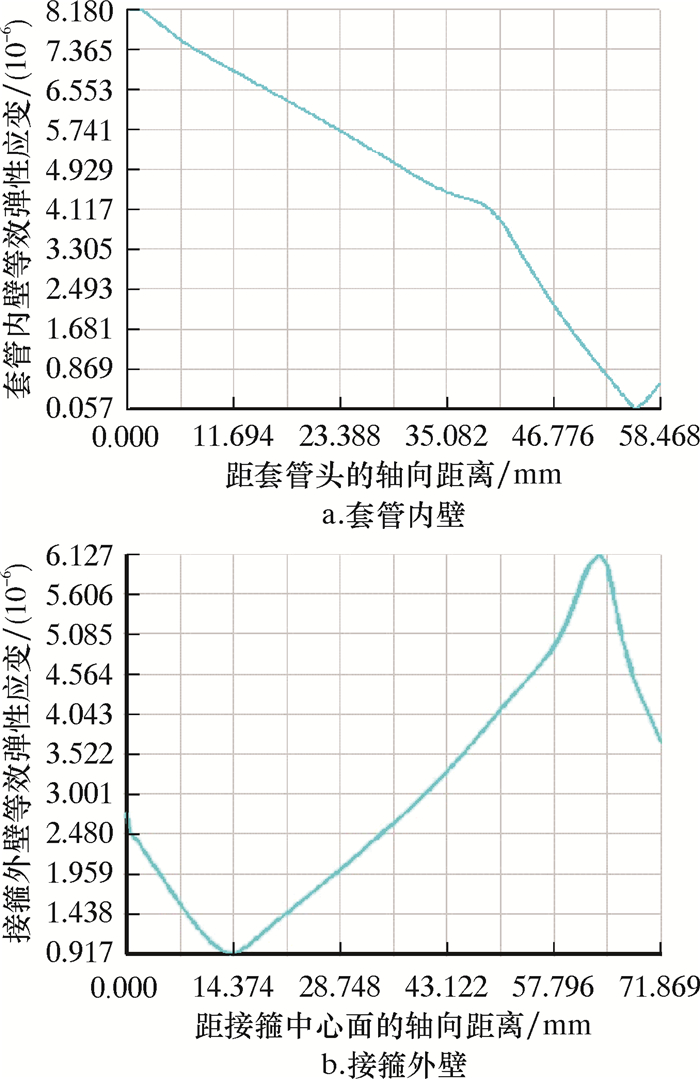
|
| 图 5 机紧3圈后套管接头内外表面等效应变沿轴向的分布 Fig.5 The equivalent strain distribution along the axial direction of the inner and outer surfaces of the casing after tightening for 3 turns |
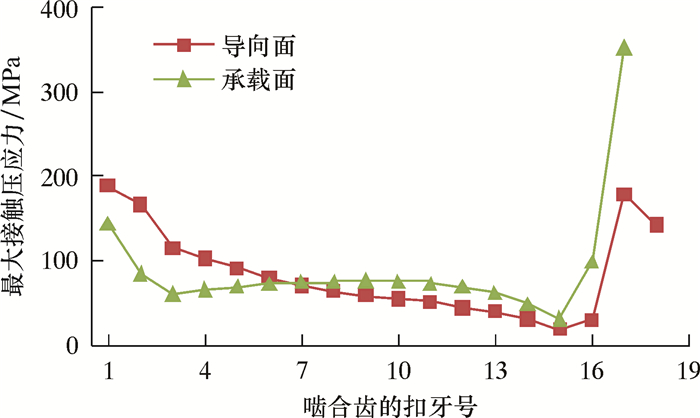
图 6为套管接头在机紧不同圈数时螺纹牙导向侧和承载侧最大法向接触压应力场的分布情况。其中螺纹啮合两端1~3和14~18扣法向接触压应力比较大,但分布不均匀,中间5~13扣接触压应力比较小,分布趋于均匀。通过分析数据可知,套管和接箍两端啮合螺纹的接触压应力是中间部分的2倍,而且接箍内螺纹的起始啮合螺纹处的接触压应力最大,其值为2.05 MPa;其次在套管外螺纹小端啮合螺纹处的最大接触压应力值为1.13 MPa。此外,机紧扭矩的大小并不改变法向接触压应力在整个螺纹啮合部位的分布状况,也就是说在机紧扭矩的作用下螺纹啮合部位的接触压应力呈现两端高、中间低的分布状态,齿面接触压应力随着上扣扭矩的增大而逐渐增高,变形也逐渐增大。
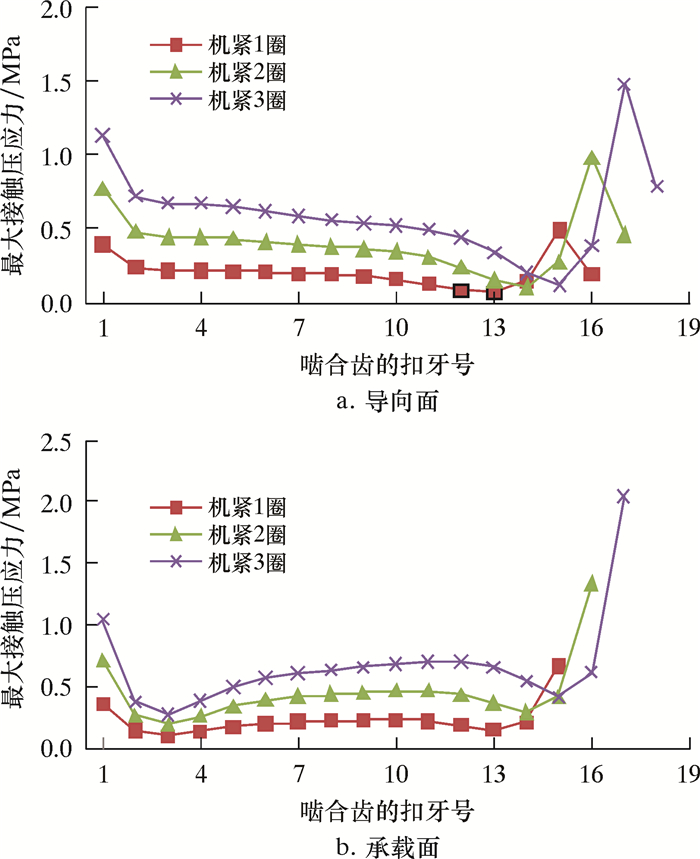
|
| 图 6 机紧过程中套管接头螺纹牙侧法向接触压应力场分布 Fig.6 Distribution of normal contact stress field in the casing joint thread in the tight process |
另外,从接箍内螺纹小端螺纹牙导向侧可以看出,其接触压应力要小于相应螺纹牙的承载侧,而在套管外螺纹小端上则相差不大,螺纹牙两侧的接触压应力在啮合螺纹的中间部位几乎相等,如图 7所示。这一现象由金属材料的泊松效应和锥管螺纹的结构特性造成。
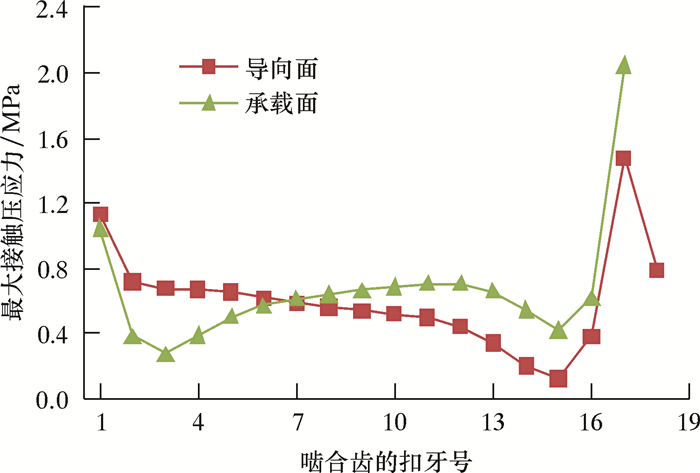
|
| 图 7 机紧3圈后螺纹牙两侧法向接触压应力分布 Fig.7 Distribution of normal contact stress of the casing thread sides after 3 turns tight |
2.2 机紧3圈后在不同内压作用下的套管螺纹连接的应力分布
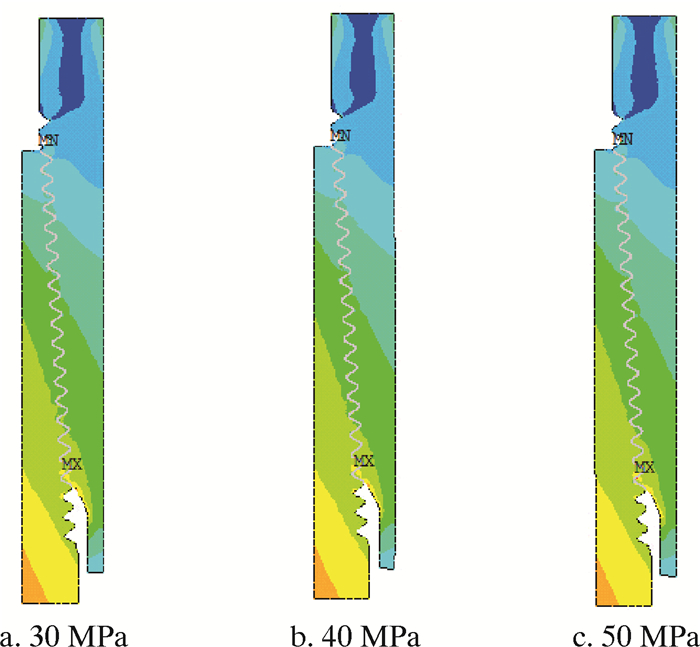
图 8为机紧3圈后在内压分别为30、40和50 MPa作用下套管接头螺纹连接部位Von Mises应力场的分布情况。模拟过程中发现,在施加内压情况下套管接箍整体应力水平明显升高,其中接箍内螺纹小端处啮合螺纹的接触压应力最大可达580 MPa。机紧3圈并施加30 MPa内压时套管接头螺纹牙两侧法向接触压应力的分布情况如图 9所示。
|
| 图 8 机紧3圈后不同内压作用下套管螺纹连接处Von Mises应力分布 Fig.8 Von Mises stress distribution of casing thread under different internal pressure after 3 turns tight |
|
| 图 9 施加30 MPa内压时螺纹牙侧法向接触压应力分布 Fig.9 Distribution of normal contact stress of the casing thread sides under the 30 MPa internal pressure |
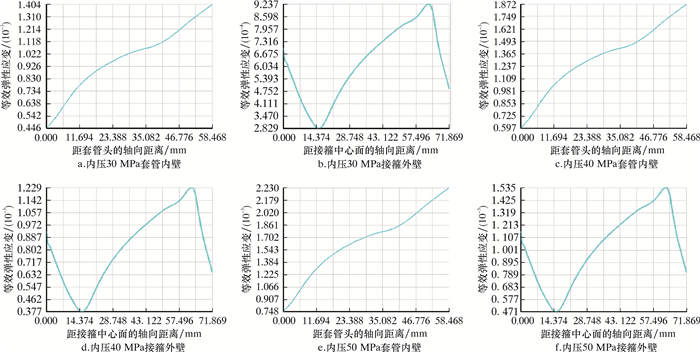
图 10为不同内压作用下套管内壁和接箍外壁等效应变沿轴向的变化曲线。
|
| 图 10 机紧3圈并在不同内压作用下套管内壁和接箍外壁等效弹性应变沿轴向的分布 Fig.10 The equivalent elastic strain distribution of casing inner wall and the joint outer wall along the axial direction after 3 turns tight and under different internal pressures |
由图 10可以看出,在不同内压作用下,接箍内螺纹小端等效弹性应变均维持在较高的水平(大于900×10-6),而在接箍内螺纹大端第1啮合扣处,其对应的管体内壁的等效弹性应变却较低(小于500×10-6);套管内壁在与管体非螺纹相对应的地方和接箍外壁与接箍起始扣相对应的地方,随着内压的增强,其表面上的等效弹性应变均明显升高,变化幅度达到150×10-6。由图中的数据可知,接箍应力水平明显低于套管应力水平,这一点与套管接头在仅受机紧扭矩作用时的接头应力场的分布情况基本相同。
2.3 机紧3圈后在不同拉应力作用下套管螺纹连接的应力分布机紧3圈后在不同拉应力F作用下套管接头圆螺纹连接Von Mises应力的分布状况如图 11所示。由图可以看出,接箍的应力水平明显要低于管体,在接箍内螺纹的第1啮合扣处螺纹牙的应力最高。套管和接箍的应力水平在拉应力逐渐增大的同时也在明显增高,当拉应力达到100 MPa时,最大等效应力为624 MPa,超过了套管的屈服强度,说明此时螺纹啮合部位已开始塑性变形。
|
| 图 11 机紧3圈并在不同拉应力作用下套管螺纹Von Mises应力分布 Fig.11 Von Mises stress distribution of the casing thread connection after 3 turns tight and under different tensile stresses |
图 12为套管接头机紧3圈后在拉应力100 MPa作用下接箍外壁和套管内壁等效弹性应变的分布情况。由于拉应力作用,内螺纹大端第1完整啮合螺纹处的应力明显升高,与其对应的接箍外壁等效弹性应变也明显增大,达到960×10-6;内螺纹小端第1啮合螺纹处对应的套管内壁等效弹性应变也明显升高,达到1 164×10-6。
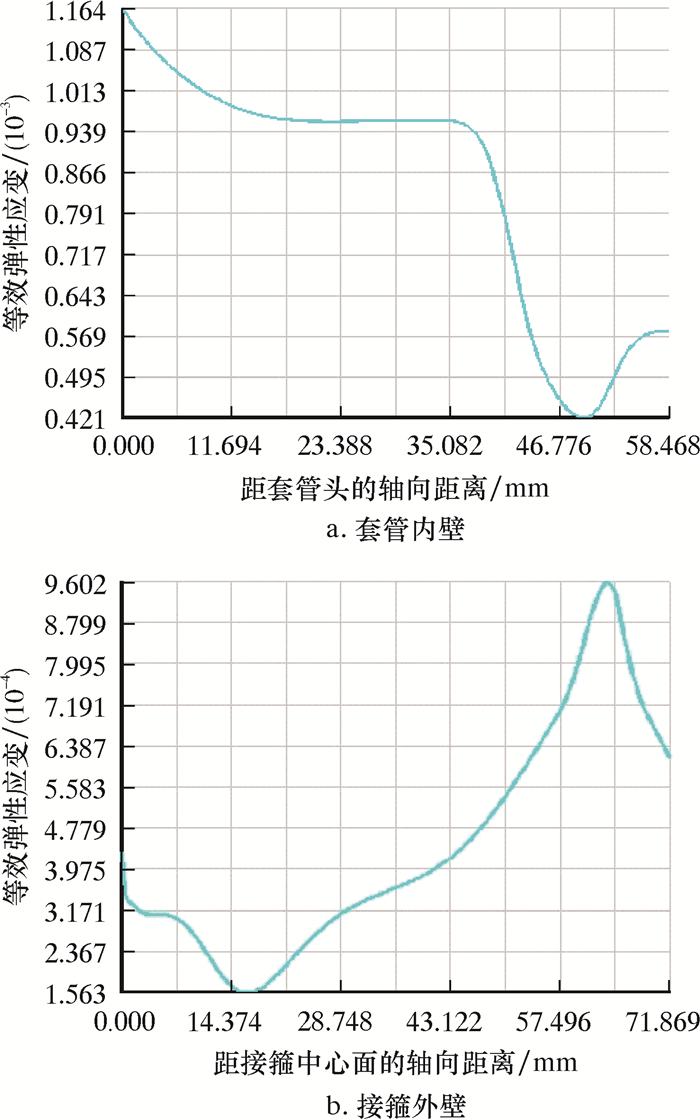
|
| 图 12 机紧3圈并在100 MPa拉应力作用下套管接头内外表面等效弹性应变沿轴向的分布 Fig.12 The equivalent elastic strain distribution of the casing joint inside and outside surface along the axial direction after 3 turns tight and under tensile stress of 100 MPa |
在拉应力为100 MPa作用下,圆螺纹套管接头内、外螺纹接触压应力发生显著变化,啮合螺纹牙承载侧的接触压应力有较大的提升,而导向面的接触应力都为0,说明在拉应力作用下,螺纹仅有一面相接触,因此在一定程度上,套管螺纹连接的密封性能被拉应力削弱了。图 13为套管螺纹接头机紧3圈并在100 MPa拉应力作用下螺纹牙两侧接触压应力的分布情况。
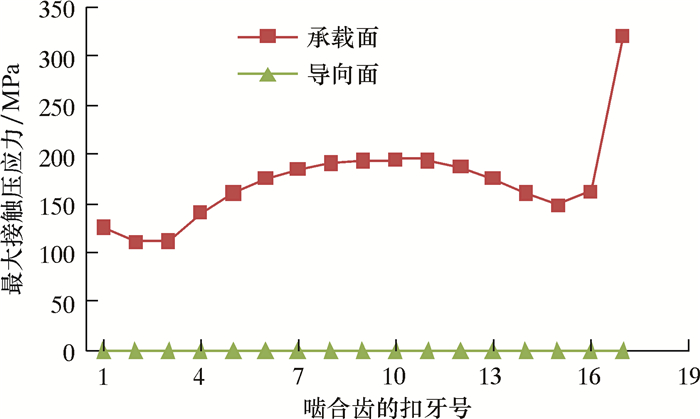
|
| 图 13 施加100 MPa拉应力时螺纹牙侧法向接触力分布 Fig.13 Normal contact stress distribution of the thread sides under 100 MPa tension force |
2.4 机紧3圈在复合工况下套管螺纹连接的应力分布
图 14为在上扣扭矩、内压和拉应力的联合作用下套管圆螺纹连接Von Mises应力的分布。由图可知,在拉应力不变的情况下,内压的增大会使套管的应力水平明显增大,接箍的应力水平也随之增大;在内压不变的情况下,拉应力增大使得套管的应力水平明显增加,接箍的应力水平基本不变。
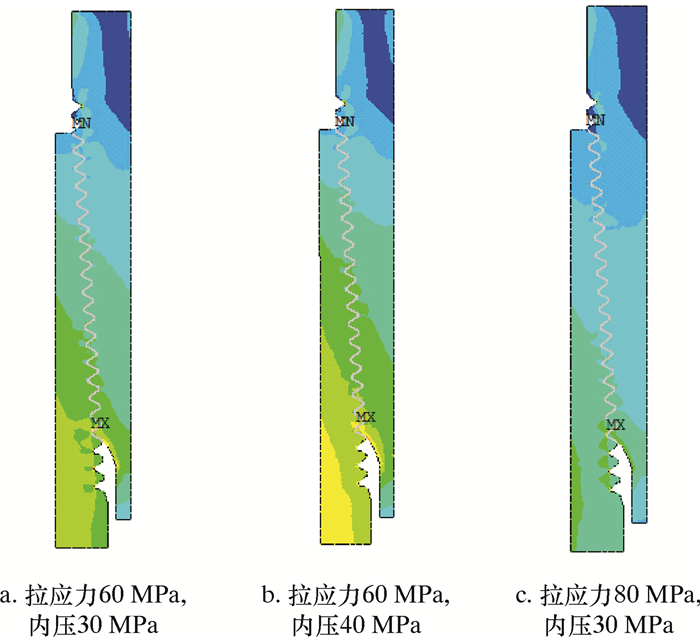
|
| 图 14 机紧3圈在拉应力和内压复合工况下套管螺纹连接Von Mises应力场的分布 Fig.14 Distribution of Von Mises stress of the casing thread after 3 turns tight and under the combination of tension force and internal pressure |
机紧3圈在轴向拉应力(60 MPa)和内压(30 MPa)联合作用下套管啮合螺纹牙两侧法向接触压应力分布情况如图 15所示。由图可知,不同复合载荷作用下外螺纹大端起始扣处的法向接触压应力仍然非常高,尤其是14~18螺纹牙两侧接触力变化幅度较大,相应也会产生较大的摩擦力,这会在套管服役时对螺纹牙表面产生较大的损伤。
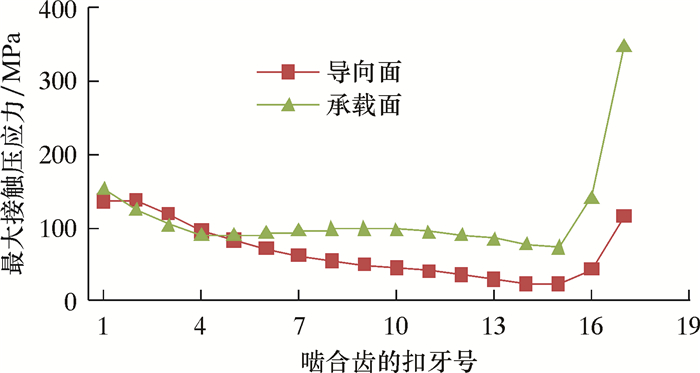
|
| 图 15 机紧3圈在拉应力60 MPa和内压30 MPa复合工况下螺纹牙两侧法向接触压应力分布 Fig.15 Normal contact compression stress distribution of the thread sides after 3 turns tight and under the tensile stress of 60 MPa and internal pressure of 30 MPa |
3 冲击载荷下套管螺纹连接分析 3.1 冲击载荷确定
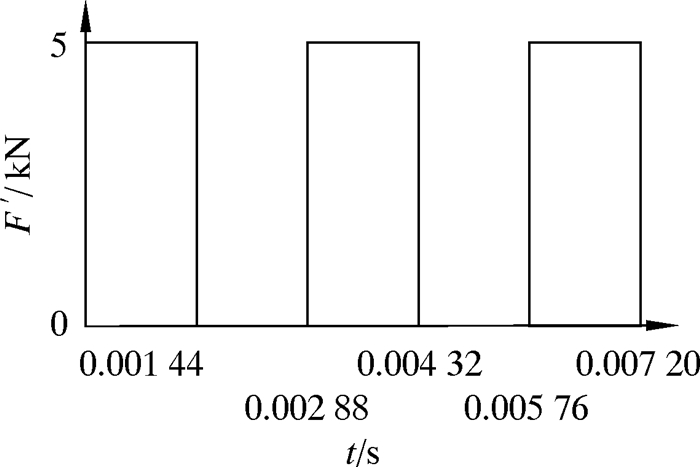
由于振荡器在套管内部运动情况复杂,对冲击载荷进行了假设,取频率为50 Hz、大小为5 kN的周期性冲击载荷施加在套管螺纹连接部分,结果如图 16所示。
|
| 图 16 冲击载荷随时间变化曲线 Fig.16 Impact load versus time |
3.2 不同工况下冲击载荷对螺纹连接的应力分析
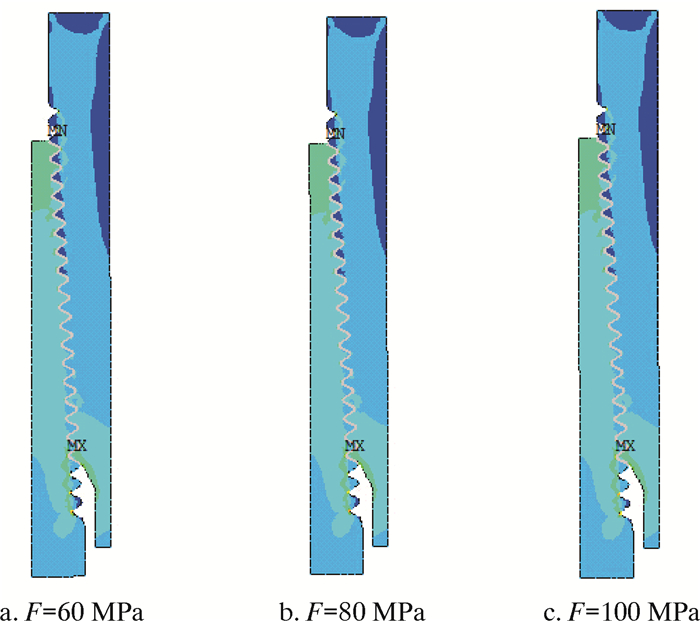
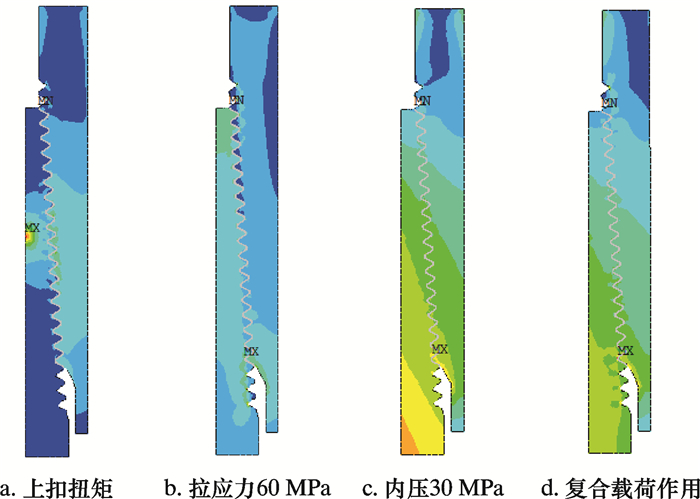
图 17为冲击载荷作用下,不同工况的套管螺纹连接的应力云图。由图可知,除上扣扭矩作用下的螺纹连接应力云图有明显的变化外,其余3种工况基本保持不变,说明在外部工况作用下,冲击载荷对套管螺纹连接部分的影响不大,不会对套管产生破坏。
|
| 图 17 冲击载荷作用下不同工况套管螺纹连接的应力云图 Fig.17 Stress distribution of casing thread under impact loads in different working conditions |
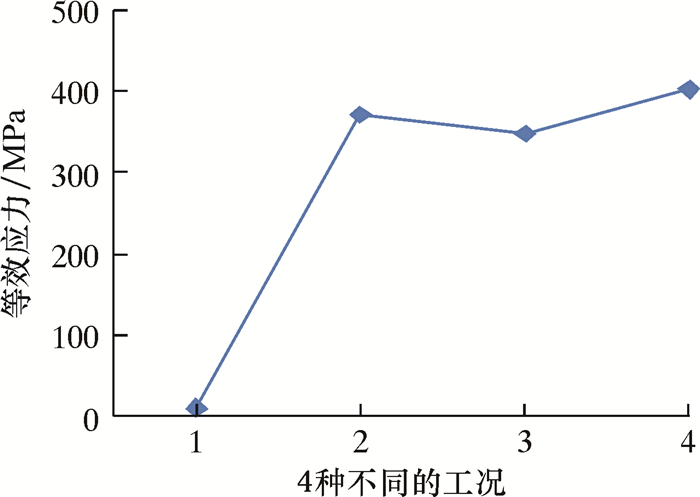
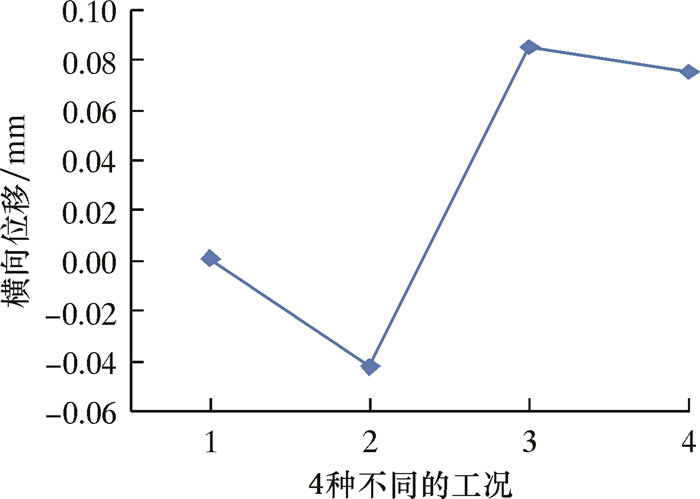
图 18和图 19中的4种不同工况如下:1表示只受上扣扭矩;2表示除上扣扭矩外,施加60 MPa的拉应力;3表示除上扣扭矩外,施加30 MPa的内压;4表示除上扣扭矩外,施加60 MPa的拉应力和30 MPa的内压。从图可知,对于工况2、3和4,冲击载荷对套管螺纹连接部分的影响很小,说明冲击载荷不会对套管产生破坏。
|
| 图 18 4种不同的工况下套管螺纹连接部分的最大Von Mises应力值 Fig.18 Maximum Von Mises stress values of the casing thread connection under four different operating conditions |
|
| 图 19 4种不同的工况下套管螺纹连接部分的最大横向位移 Fig.19 Maximum transverse displacement of the casing thread connection under four different operating conditions |
4 结论
(1) 在上扣扭矩、轴向拉伸及内压等复合载荷作用下,套管内外螺纹接触应力均出现两头高中间低的分布状态,尤其是接箍起始螺纹牙和套管外螺纹大端配合部位比较容易出现应力集中现象;随着上扣扭矩的增加、轴向拉应力的加大以及内压的增高,套管螺纹连接部分整体Von Mises应力均呈现升高的趋势,并且套管内壁和接箍外壁的等效弹性应变也在逐渐增大;螺纹牙承载侧的接触压应力要普遍高于导向侧。
(2) 在不同工况下冲击载荷对套管螺纹连接部分的应力影响较小,同时可以看出套管振荡器产生的周期性冲击载荷不会对套管造成破坏。
| [1] | 于桂杰. 长效地应力机制下套管应力与抗挤强度理论研究[D]. 青岛: 中国石油大学(华东), 2009. http://cdmd.cnki.com.cn/article/cdmd-10425-2009221538.htm |
| [2] | 夏宏南. 振动固井装置的设计及振动传播规律的研究[D]. 荆州: 长江大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10489-1012453372.htm |
| [3] | 李玉海, 赵立新, 王军荣. 振动固井技术综述[J]. 石油钻采工艺, 1994, 16(6): 40–42. |
| [4] | 袁光杰. API圆螺纹接头力学性能的数值仿真与实验研究[D]. 上海: 上海交通大学, 2014. http://d.wanfangdata.com.cn/Thesis_Y671620.aspx |
| [5] | 马永才. 油管螺纹连接上扣状态受力分析[J]. 中国材料科技与设备, 2008(3): 80–83. |
| [6] | 于艳艳. 油管螺纹失效机理分析及液压钳的技术改造[D]. 东营: 中国石油大学(华东), 2007. http://cdmd.cnki.com.cn/Article/CDMD-10425-2007226993.htm |
| [7] | YUAN G J, YAO Z Q, CHEN P, et al. Experiment and parametric design of petroleum back-pressured hydraulic impactor[J]. Journal of Dong Hua University, 2005, 22(5): 100–106. |
| [8] | 张波. ANSYS有限元数值分析原理与工程应用[M]. 北京: 清华大学出版社, 2005. |
| [9] | API.Specification for threading, gauging, and thread inspection of casing, tubing, and line pipe threads:API SPEC 5B-2008[S]. Washington DC:American Petroleum Institute, 2008. |
| [10] | 陈守俊, 桑胜举, 张毅, 等. 套管螺纹牙齿面接触应力分布研究[J]. 泰山学院学报, 2010, 32(3): 49–55. |
| [11] | 王治国, 张毅. API圆螺纹油管接头上扣与拉伸过程的有限元应力分析[J]. 钢管, 2001, 30(3): 20–25. |
| [12] | 习俊通, 聂钢, 梅雪松, 等. 套管螺纹接头连接性能的接触有限元分析[J]. 西安交通大学学报, 1999, 33(11): 63–66. DOI: 10.3321/j.issn:0253-987X.1999.11.016 |
| [13] | 王治国, 张毅. API圆螺纹接头上扣过程中螺纹齿面接触应力有限元分析[J]. 石油专用管, 1999(2): 12–17. |
| [14] | 马文博. 基于接触分析的凸度滚子轴承力学特性研究与结构优化[D]. 南京: 南京航空航天大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10287-2010080752.htm |



