0 引言
径向钻井技术也可称为超短半径径向水平井技术,该技术可实现在套管内由垂直钻进转向水平钻进,形成曲率半径远小于超短半径水平井的水平井眼。该技术主要分为套管开窗和径向水平钻进2个阶段,套管开窗主要是利用高压磨料射流或者机械方式钻开套管和水泥环,此后采用自进式喷嘴携带高压软管,利用高压水射流破岩方式持续径向水平钻进。
新型径向钻井技术可在同一口直井钻出24条辐射状的分支水平井,每条分支水平井的直径超过50 mm,长度超过100 m,同时可在同一直井形成多个层位的分支水平井,对于油田未枯竭区剩余油的开采和非常规油气田的开发具有很好的应用前景。研究表明,径向钻井技术可以将同一垂直井的产量提高2~4倍,应用效果较好的区域甚至可以达到10倍,该技术为世界油气资源的开采做出了巨大贡献[1-8]。
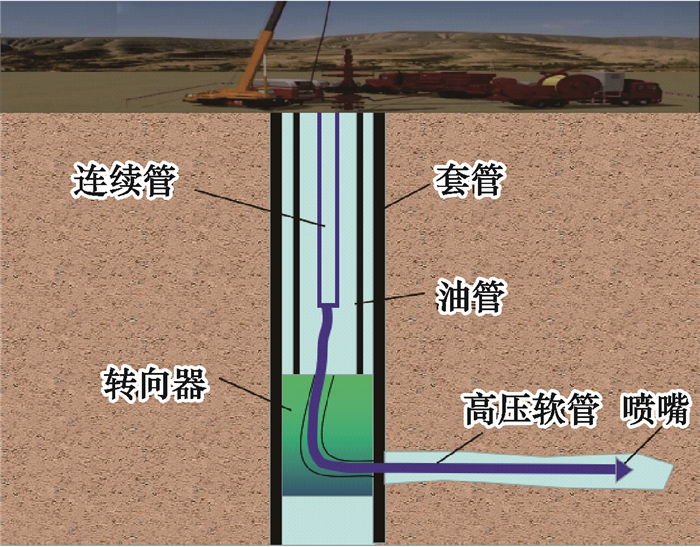
1 转向阻力分析对于径向钻井工艺,其衡量工艺优劣的主要参数为水平进尺。水平进尺的长度对工艺的增产效果有较好的促进作用。径向钻井的水平钻进工艺见图 1。自进式喷嘴有前、后向喷嘴孔,后向喷嘴孔可以产生向前的自进力,从而带动高压软管在地层中持续钻进,前向喷嘴孔主要用于破岩。由于高压软管质地柔软,若连续管对其产生较大的推力,有可能使软管曲屈,从而使高压软管与油管内壁的摩擦力增大,所以后端的连续管并不能产生很大的推力,高压软管的牵引力主要由喷嘴的自进力提供。
|
| 图 1 径向钻进示意图 Fig.1 Schematic of radial drilling |
根据文献[9],对于自进式喷嘴的自进力,主要受喷射流量与井眼直径的影响,当井眼直径为50 mm,喷射流量为0.71~0.99 L/s时,喷嘴能提供的自进力为70~130 N,同时喷射流量越大,自进力越大,而井眼直径越大,喷嘴的自进力则越小。对于自进力的消耗,主要分为以下2部分:① 高压软管通过转向器时发生弯曲,由于有转向阻力,所以与转向器内壁摩擦产生较大的摩擦阻力;② 随着水平进尺的不断增大,高压软管与地层的摩擦力也越来越大,限制了最大水平进尺。
由于高压软管与地层间的摩擦力较难控制,从而可以通过控制高压软管经过转向器的转向阻力来设计较为合理的转向滑道轨迹,以降低转向阻力,减少自进力在转向器内部的消耗,进而获得更大的水平进尺,强化工艺的增产效果。
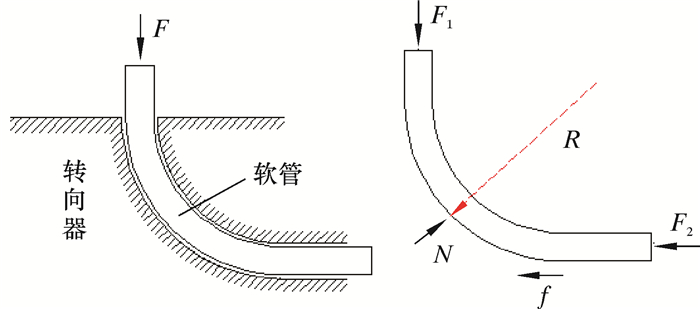
1.1 高压软管的转向受力分析高压软管受力分析如图 2所示。高压软管通过转向器时,主要受以下力的作用:F1为连续管对高压软管产生的推力(较小);N为转向器内壁对高压软管的正压力;f为高压软管通过转向器时的摩擦力,f=μN,μ为摩擦因数;F2为自进式喷嘴的牵引力(主要动力)。
|
| 图 2 高压软管受力分析简图 Fig.2 Force analysis of high pressure hose |
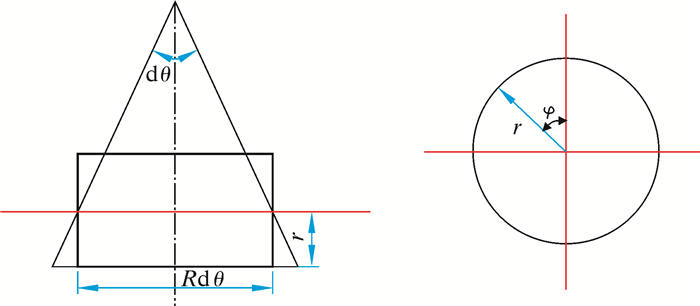
当高压软管在转向器内部滑道发生完全变形时,弯曲段的受力变形分析如图 3所示。若以软管的中心线为界,则靠近弯曲中心的部分呈受压状态,远离弯曲中心的部分呈受拉状态。
|
| 图 3 软管转向受力分析 Fig.3 Force analysis of the hose through the whipstock |
取一小段管道微元段Rdθ进行分析。图 3中R为转向器滑道半径,r为高压软管半径。同时设t为高压软管壁厚,σs为高压软管屈服强度,则软管通过弯曲轨道所需的转向阻力F为[10]:
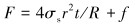
|
(1) |
由式(1) 可知,忽略摩擦力的影响,则转向阻力的大小主要与弯曲半径的大小成反比关系,因此取较大的弯曲半径能更好地降低转向阻力。对于单向弯曲的圆弧,文献[11]的研究表明:无论采取从大到小、从小到大、从大到小再到大、从小到大再变小的曲率半径,其转向阻力的值均大于¼的单段圆弧。
1.2 S形转向轨迹分析根据上述分析,对于单向弯曲的转向轨迹,当其轨迹为¼段的圆弧轨迹时,转向阻力最小。同时,由于转向阻力的大小主要与弯曲半径的大小成反比关系,为了在条件允许的范围内,扩大其转向半径,降低转向阻力,选择转向半径更大的双向弯曲S形转向轨迹。
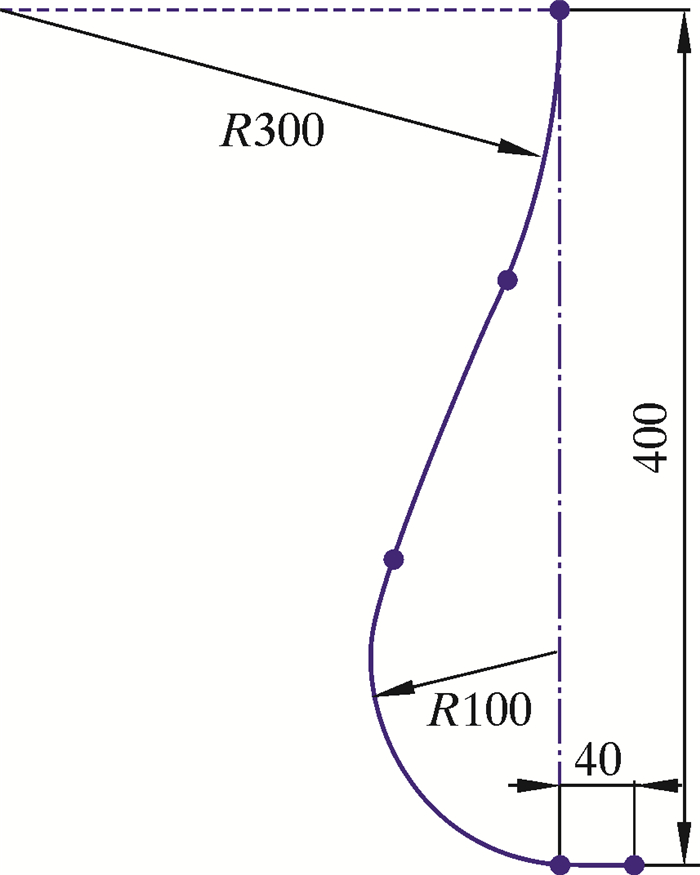
图 4为双弯曲S形曲线。主要的控制参数有导弯偏角θ,导弯半径R1,过渡段长度L1,转向半径R,矫直长度L。则有:
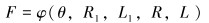
|
(2) |
|
| 图 4 双弯曲S形轨迹示意图 Fig.4 Schematic diagram of double curved S-shaped trajectory |
由于影响转向阻力的参数较多,笔者采取有限元软件ABAQUS对转向阻力进行模拟仿真分析。
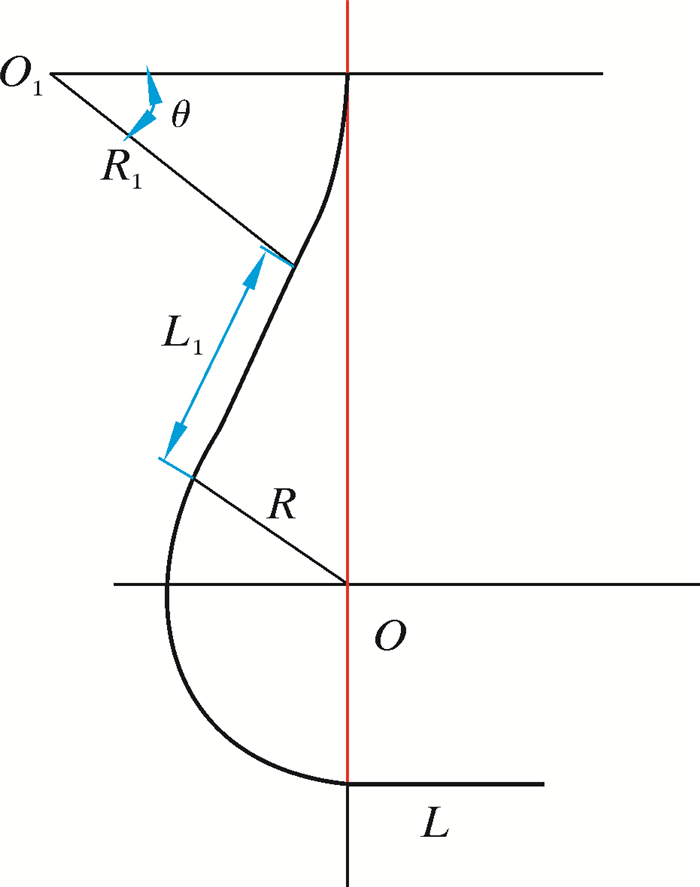
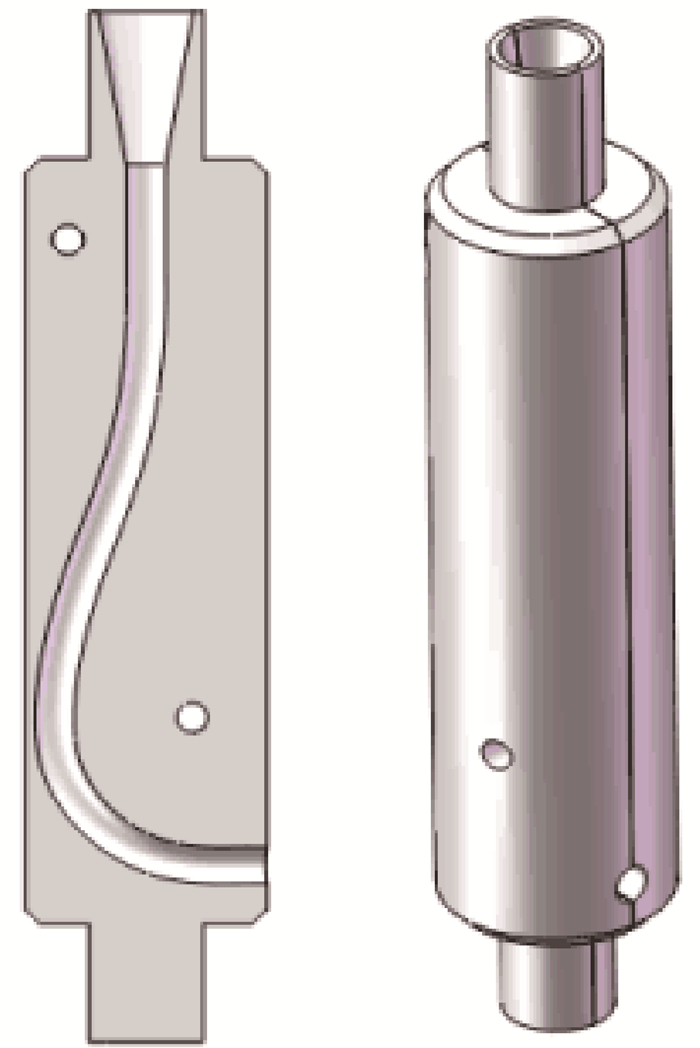
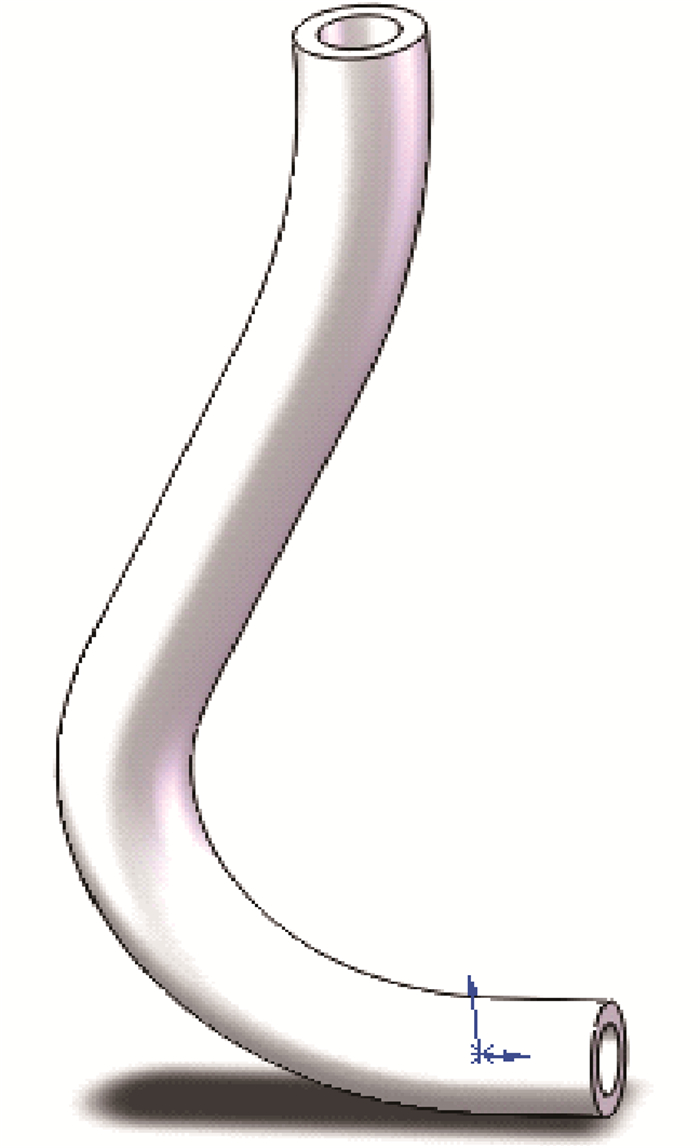
2 转向轨迹的建模与仿真分析 2.1 转向轨迹的建模根据图 5建立转向轨迹草图,考虑到转向器的实际尺寸,选取导弯半径R1=300 mm,导弯偏角θ=30°,转向半径R=100 mm。考虑转向器最大外径的实际尺寸约为160 mm,建模时控制横向尺寸:R+L≤140 mm,所以取矫直长度L=40 mm,同时控制转向器轨迹模型的纵向尺寸为400 mm。真正的转向轨迹如图 6所示,主要是在转向器内部加工完成。考虑到建模和仿真分析的简化,将转向器模型简化为图 7中环形绕转向轨迹扫描而成的管模型。其次延长转向器模型顶部,以便于在仿真分析时,若软管发生弯曲变形,避免其弯曲形态不确定造成的计算不收敛情况。同时建模参数如表 1所示。
|
| 图 5 转向轨迹草图 Fig.5 Sketch of whipstock trajectory |
|
| 图 6 转向器的真实模型 Fig.6 The true model of the whipstock |
|
| 图 7 建模采用的转向器模型 Fig.7 Model of whipstock used in modeling |
| 名称 | 内径/ mm |
外径/ mm |
弹性模量/ MPa |
泊松比 | 摩擦因数 |
| 高压软管 | 10 | 20 | 300 | 0.4 | 0.3 |
| 转向器模型 | 25 | 40 | 210 000 | 0.3 | 0.3 |
建模说明:
(1) 在实际径向钻井作业中,软管内部存在30~40 MPa的作业压力,考虑到内压只是加强了软管的刚度,对于转向规律本身的影响较小,为了建模和仿真分析的简化,采取无内压模型研究。
(2) 对于高压软管的材料参数,由于目前所用的承高压软管多用中心层为钢丝缠绕形式,以提高其内承压能力,所以高压软管多用复合材料,其弹性模量的测定较为复杂。根据文献[12-13],取高压软管的弹性模量参考值为300 MPa。由于承高压软管基材多用聚氨酯类材料,参考聚氨酯的物理性能取泊松比为0.4,同时文献[14]测定了不同硬度的聚氨酯弹性体材料与有油钢丝绳间的摩擦因数为0.15~0.35,故取高压软管与转向器间的摩擦因数参考值为0.3。
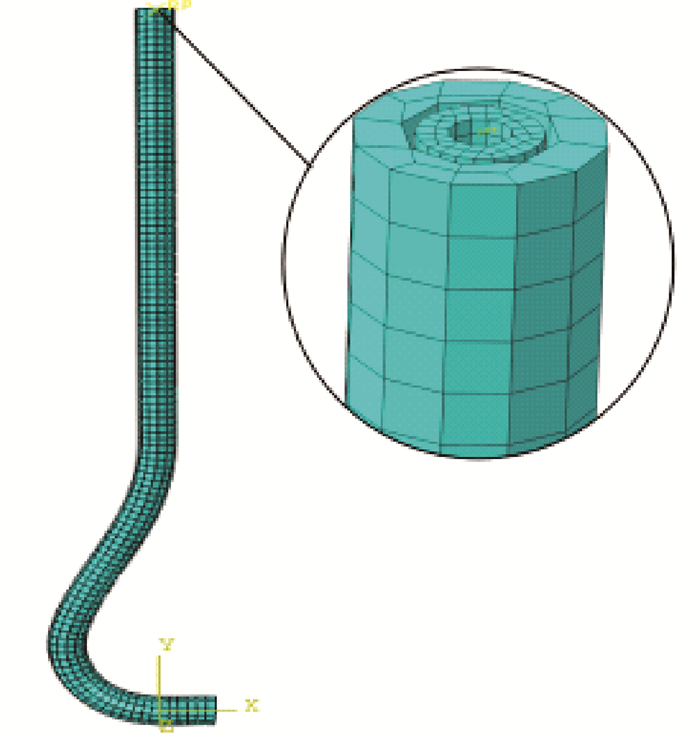
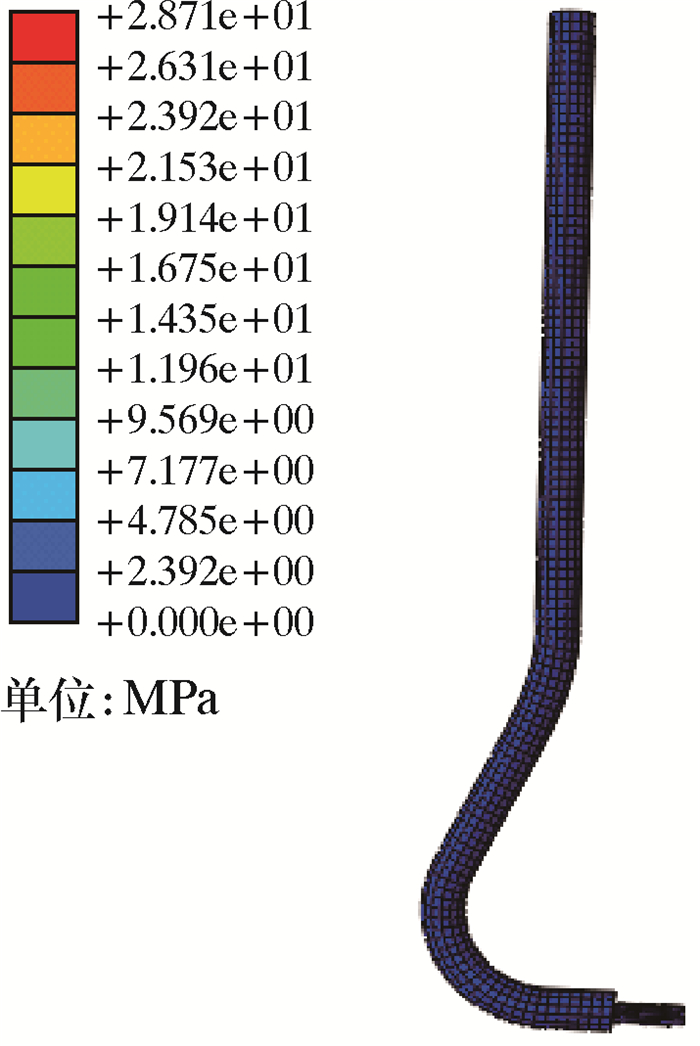
2.2 模型的仿真分析转向器网格模型如图 8所示。在分析设置过程中,边界条件的设置为:对于转向器模型,采取完全固定的边界条件,对于内部的高压软管,约束其上表面,使其只能产生垂直向下的位移,其他方向的位移和所有转角均为0。同时载荷条件为:给予高压软管上表面一个向下的位移,使其能够顺利从转向器内部穿过,观察和记录上表面所产生的反作用力,该力的大小反映了在产生特定的位移条件下所需要的力的大小,所以此时高压软管上表面所受的反作用力即为其通过转向器滑道时所需的转向阻力。图 9为分析完成后的模型图。
|
| 图 8 转向器网格模型 Fig.8 Mesh model of whipstock |
|
| 图 9 分析完成后的模型图 Fig.9 The model after finishing analysis |
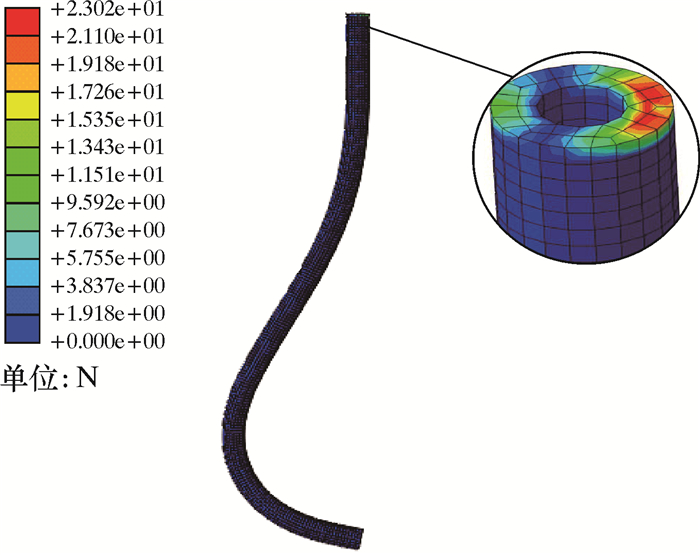
软管最大转向阻力仿真结果如图 10所示。在给定参数(导弯半径R1=300 mm,导弯偏角θ=30°,转向半径R=100 mm)的情况下,最大转向阻力为23.02 N。为了研究这3个参数对转向阻力的综合影响规律,采取参数敏感性分析,依次改变这3个量的值,观察其对转向阻力的影响。
|
| 图 10 软管最大转向阻力仿真结果 Fig.10 Simulation results of maximum steering resistance of hose |
2.3 不同参数对转向阻力的影响
依次改变导弯半径、导弯偏角以及转向半径。通过大量的仿真计算,得到如表 2所示的数据。
| R/mm | R1/mm | θ/(°) | F/N |
| 80 | 200 | 30 | 29.26 |
| 100 | 200 | 30 | 26.12 |
| 120 | 200 | 25 | 23.93 |
| 140 | 200 | 25 | 20.71 |
| 100 | 300 | 30 | 23.02 |
| 100 | 350 | 25 | 21.64 |
| 100 | 400 | 30 | 20.64 |
| 120 | 300 | 20 | 21.52 |
| 100 | 300 | 25 | 22.78 |
| 100 | 300 | 40 | 25.23 |
2.4 数据处理
对表 2中的数据,采取回归分析法[15-16],建立二次回归方程:
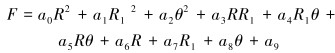
|
(3) |
将表 2中的数据带入式(3),可以得到10个方程组,采用矩阵的形式,方程组可以表示为:
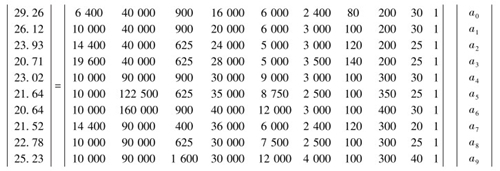
|
(4) |
采用MATLAB求解该方程组,得解为:
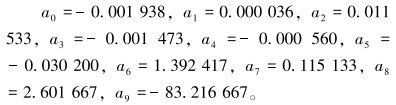
|
因此有:

|
(5) |
为了研究各影响参数的独立影响规律,采用控制变量法控制导弯半径、导弯偏角和转向半径中的任意2个参数,同时让另外一个参数在合理范围内变化,并将数值带入式(5),则可求出相应的转向阻力数值,并可以以此得出相应的影响规律。
3.1 转向半径的影响规律取导弯半径R1=300 mm,导弯偏角θ=30°,转向半径R在70~140 mm范围内变化时,通过数值计算,得出相应的转向阻力值,如表 3所示。
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| R/mm | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 |
| F/N | 31.37 | 29.11 | 26.26 | 23.02 | 19.40 | 15.39 | 10.99 | 6.20 |
根据表 3中的数据,绘制转向半径R关于转向阻力F的关系曲线,如图 11所示。由图可知,随着转向半径的增大,转向阻力随之减小,并且减小的幅度较大,可知转向半径R的大小是转向阻力F最主要的影响参数。
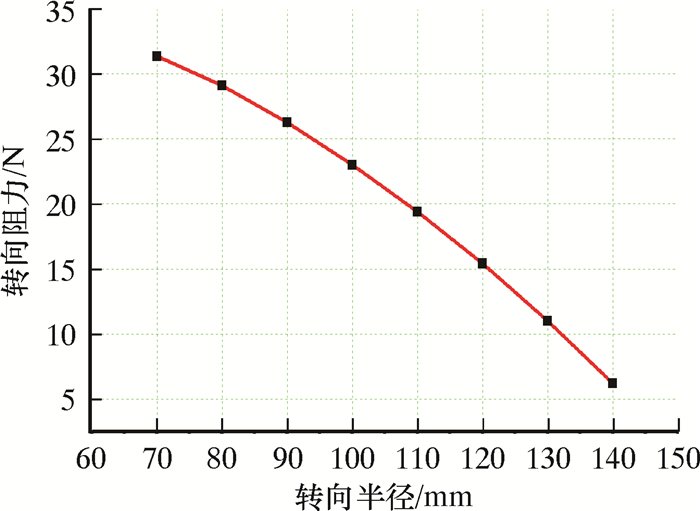
|
| 图 11 F-R关系曲线 Fig.11 F-R relationship curve |
3.2 导弯半径的影响规律
取转向半径R=100 mm,导弯偏角θ=30°,导弯半径R1在200~400 mm范围内变化时,通过数值计算,得出转向阻力值,如表 4所示。
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 |
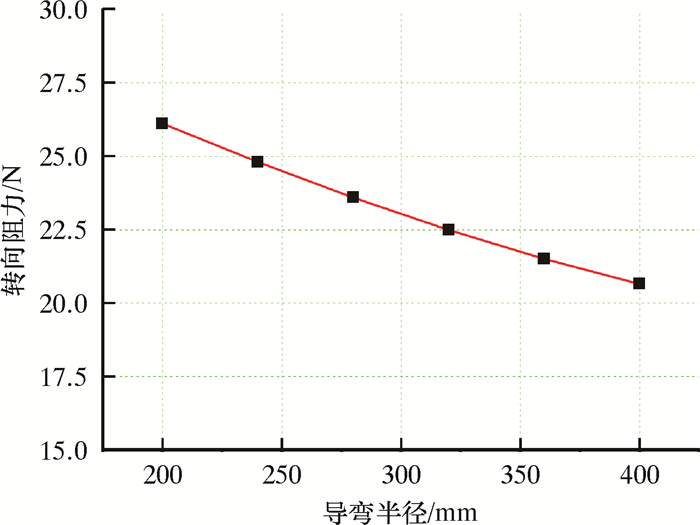
| R1/mm | 200 | 240 | 280 | 320 | 360 | 400 |
| F/N | 26.12 | 24.80 | 23.59 | 22.49 | 21.51 | 20.65 |
根据表 4中的数据,绘制导弯半径R1关于转向阻力F的关系曲线,如图 12所示。由图可知,转向阻力随着导弯半径的增大而减小。但是对比图 10的结果可知,其随着导弯半径的增大,转向阻力的减小幅度并不大。相比于转向半径,导弯半径对转向阻力的影响较小,并不是转向阻力的主要影响参数。
|
| 图 12 F-R1关系曲线 Fig.12 F-R1 relationship curve |
3.3 导弯偏角的影响规律
取转向半径R=100 mm,导弯半径R1=300 mm,导弯偏角θ在15°~40°范围内变化时,通过数值计算,得出相应的转向阻力值,结果如表 5所示。
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 |
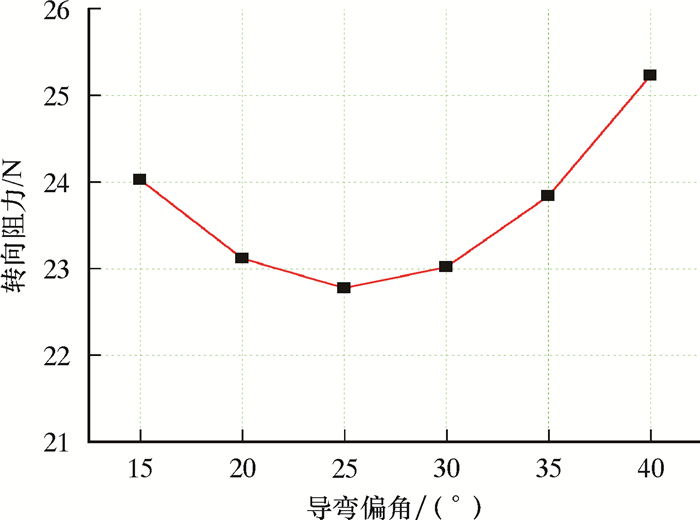
| θ/(°) | 15 | 20 | 25 | 30 | 35 | 40 |
| F/N | 24.03 | 23.12 | 22.78 | 23.02 | 23.84 | 25.23 |
根据表 5中的数据,绘制导弯偏角θ关于转向阻力F的关系曲线,如图 13所示。
|
| 图 13 F-θ关系曲线 Fig.13 F-θ relationship curve |
由图 13可知,转向阻力随着导弯偏角的增大,呈先减小后增大的趋势,且转向阻力F的最小值在导弯偏角θ=25°附近出现。尽管如此,由数值大小可以看出,当导弯偏角θ在15°~40°范围内变化时,转向阻力的幅值改变量很微弱,所以导弯偏角对转向阻力的影响较小,并不是影响转向阻力大小的主要参数。
4 结论(1) 通过仿真分析,对转向半径R、导弯半径R1和导弯偏角θ对转向阻力F的综合影响进行了研究,研究结果表明:转向阻力随着转向半径的增大而减小,是转向阻力的主要影响参数;转向阻力随着导弯半径的增大而减小,但是减小幅度较小,并不是转向阻力的主要影响参数;转向阻力随着导弯偏角的增大,呈先减小后增大的趋势,转向阻力F的最小值在导弯偏角θ=25°附近出现,但是导弯偏角对转向阻力的幅值影响很小,并不是转向阻力的主要影响参数。
(2) 所研究的转向器基于在ϕ177.8 mm套管内完成垂直至水平转向,考虑到转向器的实际尺寸要求,最终选择转向器的转向轨迹参数为:转向半径R=100 mm,导弯半径R1=400 mm,导弯偏角θ=30°。
| [1] | 迟焕鹏, 李根生, 黄中伟, 等. 水力喷射径向水平井技术研究现状及分析[J]. 钻采工艺, 2013, 36(4): 119–124. |
| [2] | 激扬. 古老钻井技术的奇葩——径向钻井[J]. 石油知识, 2015(3): 12–13. |
| [3] | MARBUN B T H, ZULKHIFLY S, ARLIYANDO L, et al. Review of ultrashort-radius radial system (URRS)[R]. IPTC 14823, 2001. |
| [4] | DICKINSON W, ANDERSON R R, DICKINSON R W. The ultrashort-radius radial system[J]. SPE Drilling Engineering, 1989, 4(3): 247–254. DOI: 10.2118/14804-PA |
| [5] | LI Y H, WANG C J, SHI L H, et al. Application and development of drilling and completion of the ultrashort-radius radial well by high pressure jet flow techniques[R]. SPE 64756, 2000. |
| [6] | BALCH R S, RUAN T, SAVAGE M, et al. Field testing and validation of a mechanical alternative to radial jet drilling for improving recovery in mature oil wells[C]//SPE Western Regional Meeting. 2016. |
| [7] | 马开良, 吴福才, 杨永印, 等. 径向井技术在韦5井的应用[J]. 钻采工艺, 2005, 28(5): 17–20. |
| [8] | 崔龙连, 汪海阁, 葛云华, 等. 新型径向钻井技术[J]. 石油钻采工艺, 2008, 30(6): 29–33. |
| [9] | 黄中伟, 李根生, 唐志军, 等. 水力喷射侧钻径向微小井眼技术[J]. 石油钻探技术, 2013, 41(4): 37–41. |
| [10] | 吴德元, 沈忠厚. 一种新型高压水力喷射径向水平钻井系统[J]. 中国石油大学学报(自然科学版), 1994, 18(2): 128–130. |
| [11] | 徐金超. 不扩孔径向水平井钻管转向机理及其优选研究[D]. 青岛: 中国石油大学(华东), 2010. http://cdmd.cnki.com.cn/Article/CDMD-10425-2010281058.htm |
| [12] | 从恒斌, 王贵桥, 郑宏伟. 液压油和软管的等效体积弹性模量测定[J]. 机床与液压, 2010, 38(5): 81–83. |
| [13] | 刘春荣. 液压软管有效体积模量的测定[J]. 液压气动与密封, 1997(3): 7–8. |
| [14] | 田雨, 张杰, 韦永继, 等. 聚氨酯弹性体摩擦系数影响因素探讨[J]. 聚氨酯工业, 2002, 17(1): 37–40. |
| [15] | 英飞. 径向水平井套管冲孔及钻管送进机理研究[D]. 青岛: 中国石油大学(华东), 2014. http://cdmd.cnki.com.cn/Article/CDMD-10425-1016711766.htm |
| [16] | 张栋. 煤层分支孔水力钻进超短半径转向机理研究[D]. 青岛: 中国石油大学(华东), 2013. http://cdmd.cnki.com.cn/Article/CDMD-10425-1015024896.htm |



