2. 中国石油集团海洋工程有限公司工程设计院
2. Engineering Design Institute, CNPC Offshore Engineering Company Limited
0 引言
管道运输是油气资源远距离输送最经济的方式。在管线敷设时,为了防止受到损伤,一般采用挖沟填埋的方法将管线保护起来。但是由于土质松软、地层差异和地壳沉降等原因常常导致管线裸露出来,裸露的悬空段容易发生腐蚀和泄漏等安全事故,对企业造成不必要的经济损失,特别是海底管线,洋流的冲刷加大了管线裸露的风险。随着国家相关部门对安全生产的日益重视,天然气管线的老化严重,管线安全检测显得尤为重要。
目前国内外管道悬空检测相对成熟的技术包括:浅地层剖面技术[1]、单/多波束光纤技术[2-3]、侧扫声呐[4-5]分布式光纤传感技术[6]和超声波检测[7]等探测技术,但这些技术不同程度地存在检测结果易受到环境噪声干扰、成本相对较高和信号衰减严重等缺点。现有的管道悬空检测技术大致可分为管外检测和管内检测。管外检测的应用更普遍,它包括人工巡线检测和其他相关技术的外检测,缺点是效率低、易受干扰、成本高。为了克服管道外检测的一些弊端,笔者采用管内主动激励的方式检测管线是否出现悬空段,悬空检测装置在管道内随清管器或拖拽设备前进的同时,进行激励信号的发生和响应信号的采集,操作简单,可以在一定程度上规避前述悬空检测技术的缺点。
1 建模与仿真模拟 1.1 模型参数设置以某段城市天然气管道为例,该管段长度31.4 km,直径0.355 m,壁厚0.006 3 m,设计压力4.0 MPa,采用的管材材质为L360,选取其中一段含有悬空段的管线为有限元模型的参数依据。根据埋地管道系统的结构特性建立模型,选取长度L=10 m含有悬空段的埋地输气管道进行分析,建立仿真模型如图 1所示。管道模型密度7 850 kg/m3、弹性模量210 GPa;模拟土壤的弹性模量设为6.5 MPa,泊松比0.35。
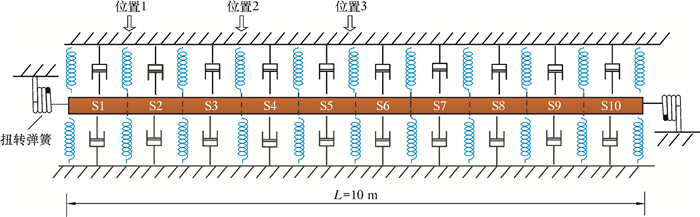
|
| 图 1 管道模型示意图 Fig.1 Schematic diagram of the pipeline model |
把整段管道分成S1~S10的10等份,分别在S2、S4、S6段支撑弹簧处建立3个用来施加激励的输入通道和获取响应的输出通道。在管道轴线方向的竖直平面内,设置上、下2排弹簧用来模拟管外土壤的支撑情况,在模型两端各设置一个扭转弹簧模拟相邻管段,扭转弹簧刚度设为1×1011 N·m/rad、阻尼为1.81×104 N·s/m。根据文献[8]中提到的相似性的方法确定弹簧刚度系数,即不断改变弹簧刚度系数使其中一段管道模型计算得到的加速度与多段(7段)管道模型得到的加速度相似,从而确定支撑弹簧刚度系数。弹簧阻尼系数可通过文献[9]中提出的收敛性研究来确定。
1.2 ADAMS软件建模在ADAMS软件中创建管道模型,设置管道物理参数,将管道离散成若干个有限单元,采用四面体单元类型。建立弹簧阻尼系统,设置弹簧刚度和阻尼等系数。根据国家天然气管线铺设标准(GB 50028—1993) 中对埋地段管线填埋深度的要求,计算出埋覆土壤对管道的作用力,在模拟弹簧上施加预紧力[10],利用ADAMS/Flex模块生成离散的管道模型,如图 2所示。
|
| 图 2 管道模型 Fig.2 Pipeline model |
1.3 软件仿真模拟 1.3.1 正弦扫频
正弦扫频试验是检测产品可靠性及各种机构振动问题的重要手段,对各类结构模态参数的识别起到重要作用,广泛应用于汽车、航天和建筑等领域。所谓的正弦扫频信号是指在一定频率段内,给予固定幅值的正弦信号振动,常用的正弦扫频信号包括线性扫描和对数扫描[11-14],考虑到试验模拟时所用扫频区间固定且范围不是很大,模拟中采用线性扫描。
在ADAMS软件中采用管内主动激励的方法对管道不同位置施加正弦扫频激励,对模型进行振动仿真,分析在不同位置的振动响应。通过对管道模型进行模态分析,得到系统每一阶模态的固有频率、阻尼和振型,根据管道在特定的频率范围内各阶主模态的特性,对管道是否存在悬空段进行初步判定。
1.3.2 振动仿真模拟根据挪威船级社(DNV)管道悬跨段设计中所涉及的有限元模型,改变管道模型悬空段长度,对不同的模型进行振动模态分析,分析悬空段的长度对系统模态的影响。
为了验证所提出的陆地管道悬空检测方法的正确性,在仿真分析中做出如下假设:① 管道材质均匀,在线性弹性范围内;② 支撑段支撑介质具有各向同性;③ 忽略管内压力对管道刚性影响;④ 激励信号处于特定频率范围内,忽略环境噪声和管内流体引起的噪声影响。
利用ADSMS/Vibration模块模拟管道受到强迫振动,首先沿管道轴线方向建立如图 2所示不同位置的输入和输出通道,在输入通道添加0.1~500.0 Hz的正弦扫频激励信号,激励幅值为1,在输出通道中设定采集竖直方向的振动响应。按照表 1所示模拟方案依次进行9组试验。表 2为不同敷设介质的弹性模量。由于不同的介质对管道的阻尼效果不同,从文献[15]中知,当模型跨肩部分长度大于0.8倍悬空长度时,继续增加跨肩部分长度对固有频率计算结果几乎没有影响,采用悬空段L=4 m,两端跨肩长度分别为3 m的悬空管道模型,如图 2b所示。表 1中算例1~5分别模拟不同悬空长度对管道共振频率的影响,算例6~9分别模拟管道周围介质参数对固有频率的影响。
| 序号 | 悬空位置 | 悬空长度/m | 支撑弹簧刚度/(N·m-1) |
| 算例1 | 无悬空 | 0 | 5.98×105 |
| 算例2 | S5 | 2 | 5.98×105 |
| 算例3 | S4~S6 | 4 | 5.98×105 |
| 算例4 | S3~S7 | 6 | 5.98×105 |
| 算例5 | S2~S8 | 8 | 5.98×105 |
| 算例6 | S4~S6 | 4 | 3.00×105 |
| 算例7 | S4~S6 | 4 | 6.00×105 |
| 算例8 | S4~S6 | 4 | 1.00×106 |
| 算例9 | S4~S6 | 4 | 5.00×106 |
| 土类 | 弹性模量 |
| 很软的黏土 | 0.30~0.35 |
| 软黏土 | 2.00~5.00 |
| 中硬黏土 | 4.00~8.00 |
| 硬黏土 | 7.00~18.00 |
| 粉质砂土 | 7.00~20.00 |
| 松砂 | 10.00~25.00 |
| 砂质黏土 | 30.00~40.00 |
| 紧砂和卵石 | 50.00~80.00 |
2 结果与分析 2.1 悬空段长度对频率响应函数的影响
频响函数描述的是系统对输入、输出谐为正弦信号的传递关系,也可以反映系统稳态输入和输出的关系。进入ADAMS/PostProcessor后处理模块,得到不同输出位置的竖直方向的振动响应频响函数图像,以分析管道悬空段长度对正弦扫频激励作用下各位置的1阶共振频率大小的影响情况。频率响应函数如图 3所示。
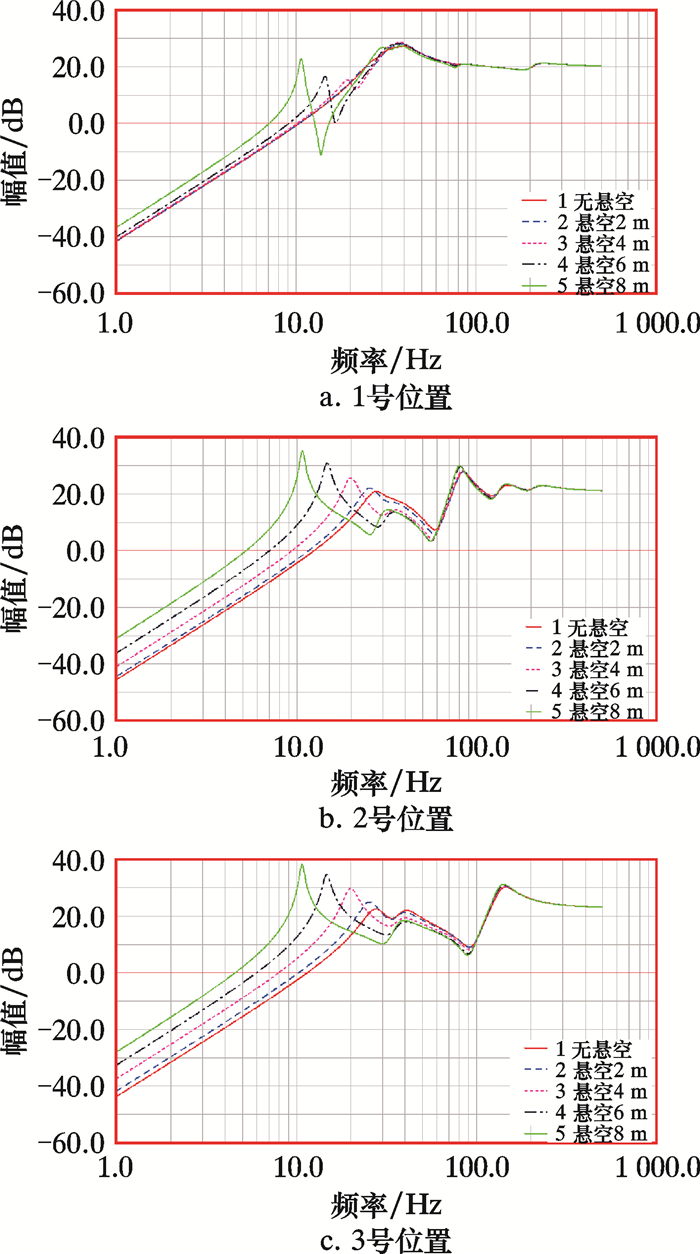
|
| 图 3 频率响应函数 Fig.3 Frequency response function |
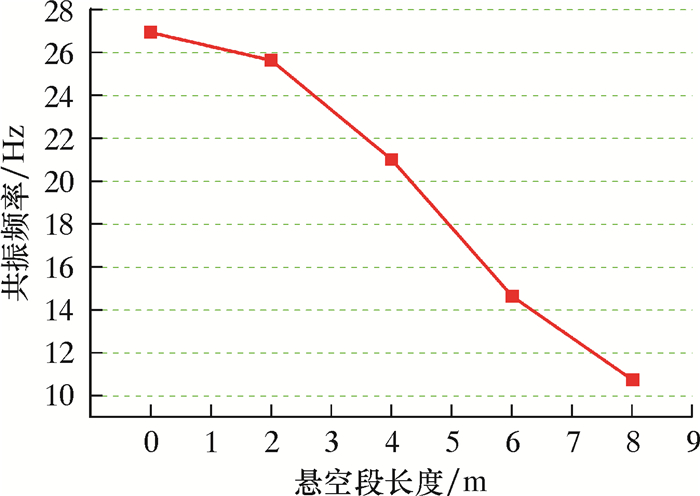
从图 3可以看到,对管道施加正弦扫频激励时,由于管道悬空段长度不同所产生的频响函数也随之变化,共振频率存在差异。当埋地管道周围支撑完好(无悬空段)时1阶共振频率为26.0 Hz,随着悬空段长度越来越长,1阶共振频率出现平移现象。管道悬空段越长,共振频率越低,当管道悬空段长度达到8 m时,管道的1阶共振频率降低到10.7 Hz。
由于模拟管道系统有多阶共振频率,所以在频响函数图谱中有多个峰值。从图 3中还可以发现,管道悬空段长度的变化主要对第1阶共振频率变化比较明显。对比3个通道频响函数图可以发现,1阶固有频率的平移趋势一致,但局部位置在频率响应函数幅值增长率方面存在差异,差异的来源主要由输出通道距离支撑弹簧的距离和支撑介质等因素造成。
结合系统振动分析结果,3个位置处1阶共振频率幅值随悬空段长度的变化情况如图 4所示。1号位置位于3个位置的最左侧,幅值变化曲线出现了先下降后上升的趋势,是因为当模拟悬空段长度分别为0、2、4、6 m时,1号位置均处于支撑状态,所以1阶共振频率的幅值没有随悬空段长度的增长而线性增高;2号位置位于3个位置的中间,模拟的是管道支撑段和悬空段交接的情况,当悬空段长度为0、2 m时处于支撑状态;当悬空段长度为6、8 m时处于悬空位置,所以在图 4中在悬空段长度为4 m时出现斜率突增现象;3号位置位于管道的中间位置,模拟时均位于悬空段,所以1阶共振频率的幅值变化近似呈线性增长。
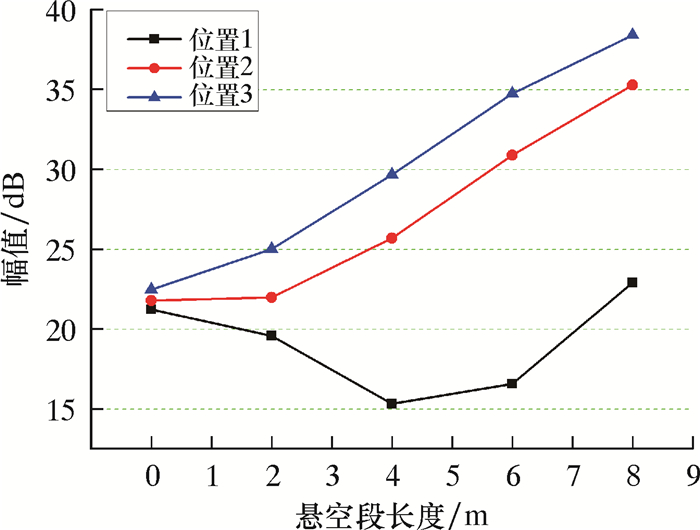
|
| 图 4 1阶共振频率幅值变化图 Fig.4 Amplitude change of the first order resonance frequency |
位置3处共振频率随悬空段长度的变化如图 5所示。从图可以看出,当管道出现悬空段时,其1阶共振频率明显减小,通过1阶共振频率值可以判断管线是否出现悬空段。
|
| 图 5 位置3处共振频率随悬空段长度的变化 Fig.5 The changes of resonant frequency at position 3 with the free span section length |
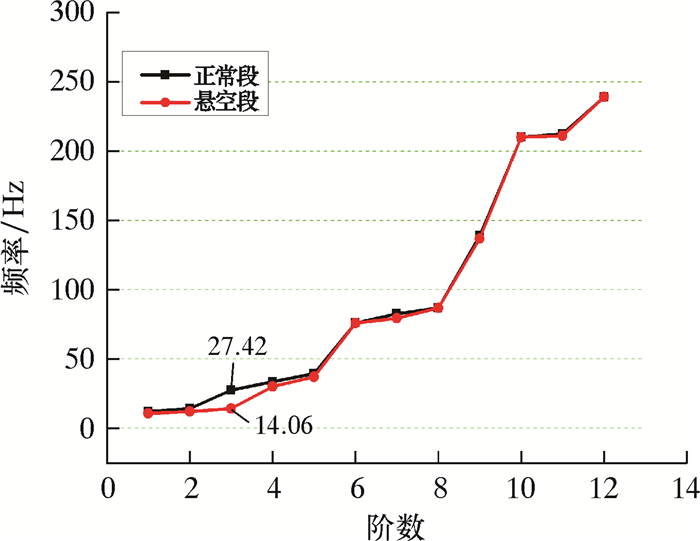
图 6给出了管道正常段和悬空段(L=4 m)的无阻尼固有频率,对比正常段和悬空段的各阶固有频率,用Δ表示模态应变差(其值等于正常段与悬空段固有频率之差),每一阶固有频率都发生了相应的变化,其中第3阶固有频率变化最大,变化量为13.4 Hz,说明第3阶固有模态在检测管道是否悬空中起到主要作用。
|
| 图 6 正常段和悬空段的各阶固有模态 Fig.6 The natural modal of each order of the normal section and the free span section |
2.2 周围介质参数对固有频率的影响
在ADAMS软件中改变支撑弹簧刚度系数模拟管道周围不同介质,依次模拟软质土壤、中硬土壤、硬质土壤和砂石介质等不同环境参数,分析介质参数对管道固有频率的影响。
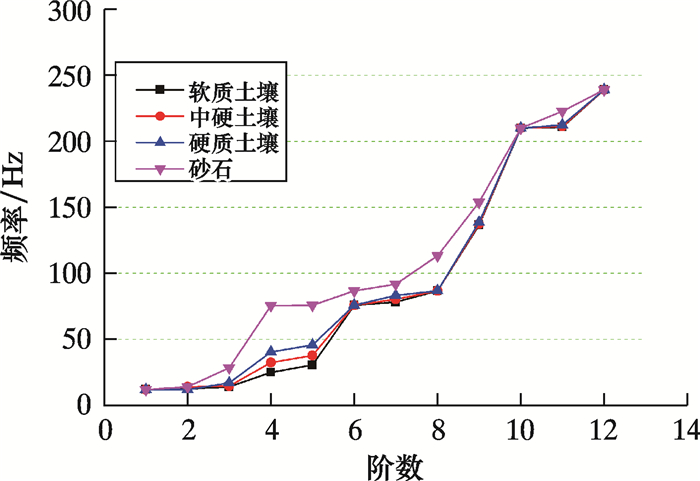
图 7给出了不同介质参数下各阶固有频率的大小。从图可以看出,软质土壤、中硬土壤和硬质土壤对管道各阶固有频率的影响较小,管道周围介质的改变主要影响的是第4阶和第5阶固有频率,从第5阶向后几乎没有影响,其中模拟的砂石介质对管道固有频率影响较为明显,但是整体来说管道周围介质对管道的固有频率影响较小。
|
| 图 7 介质参数对模型固有频率的影响 Fig.7 Effect of media parameters on the natural frequency of the model |
2.3 模态参与因子分析
通过ADAMS软件进行受迫振动分析,可以得到频率响应的峰值。该峰值由各阶模态叠加而成,模态参与因子就是找出峰值处由哪几阶主要的模态叠加而成,并且按照要求输出其中贡献较大的几阶模态值。
对比正常段和悬空段各阶共振点所对应的模态参与因子,分别如图 8和图 9所示。在正常段主要是第3、5、9阶模态起到主要作用,悬空段主要是第1、9阶起到主要作用;从正常段到悬空段的变化过程中,在第1阶共振频率处起主要作用的固有模态从第3阶变成第1阶。正常段和悬空段主要模态振型如表 3所示。由表可知,对应的固有频率从27.4 Hz减小到10.7 Hz。从图 8和图 9中可以发现各阶固有模态在共振点处贡献量的大小。参照表 3可知共振时各阶振型。

|
| 图 8 正常段频响函数和模态参与因子 Fig.8 Frequency response function and modal participation factor of the normal section |

|
| 图 9 悬空段频响函数和模态参与因子 Fig.9 Frequency response function and modal participation factor of the free span section |
| 管道状态 | 模态振型 | 振型说明 |
| 正常段 |  |
3阶垂直弯曲 |
| 正常段 |  |
5阶垂直弯曲 |
| 正常段 |  |
9阶垂直弯曲 |
| 悬空段 |  |
1阶扭转 |
| 悬空段 |  |
9阶弯扭 |
3 结论
(1) 悬空段长度对管线1阶共振频率影响较大,悬空段长度越长,共振频率越低;随着悬空段长度的增加,共振频率逐渐减小,出现共振频率的平移现象,可通过振动频响函数图中的第1阶共振频率的改变来判断管道的悬空状况。
(2) 管道敷设周围介质影响管道固有频率,起作用的主要是模型前几阶固有频率,土质越硬,管道系统固有频率越高,但综合考虑,土壤介质对管线固有频率的影响不大。
(3) 从模态参与因子上分析可知,1阶共振频率在支撑段由第3阶固有模态起主要作用,悬空段由第1阶固有模态起主要作用,基于1阶共振频率变化的模态分析对管道悬空检测方法可为海底悬空管道内检测技术提供指导。
| [1] | 蔡春麟, 张异彪, 顾兆峰. 参量阵浅地层剖面技术在海底管道检测中的应用[J]. 海洋地质前沿, 2007, 23(4): 38–42. |
| [2] | 来向华, 潘国富, 傅晓明, 等. 单波束测深技术在海底管道检测中应用[J]. 海洋工程, 2007, 25(4): 66–72. |
| [3] | 来向华, 马建林, 潘国富, 等. 多波束测深技术在海底管道检测中的应用[J]. 海洋工程, 2006, 24(3): 72–77. |
| [4] | 王雷. 海底管道悬空检测及治理技术研究[D]. 东营: 中国石油大学(华东), 2014. http://mall.cnki.net/magazine/article/HYJS198803014.htm |
| [5] | 柳黎明. 基于侧扫声纳系统的海底管道检测技术研究[D]. 杭州: 中国计量学院, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10356-1014378057.htm |
| [6] | 潘坤. 应用于石油管道安全检测的分布式光纤传感系统基础研究[D]. 成都: 电子科技大学, 2011. |
| [7] | 周燕, 董怀荣, 周志刚, 等. 油气管道内检测技术的发展[J]. 石油机械, 2011, 39(3): 74–77. |
| [8] | PENG X L, HAO H, LI Z X. Application of wavelet packet transform in subsea pipeline bedding condition assessment[J]. Engineering Structures, 2012, 39(6): 50–65. |
| [9] | PENG X L, HAO H. Damage detection of underwater pipeline using vibration-based method-nmerical simulation[C]//The 3rd World Congress on Engineering Asset Management and Intelligent Maintenance Systems Conference, U.K., Springer-Verlag London Ltd. CD-Rom, 2009:1262-1274. |
| [10] | MAGALHÃES F, CUNHA A, CAETANO E. Vibration based structural health monitoring of an arch bridge:From automated OMA to damage detection[J]. Mechanical Systems & Signal Processing, 2012, 28(2): 212–228. |
| [11] | 胡志强. 随机振动试验应用技术[M]. 北京: 中国计量出版社, 1996. |
| [12] | 田光明, 陈光. 正弦扫描振动响应的时频分析[J]. 振动与冲击, 2005, 24(6): 13–16. |
| [13] | 刘昶, 李玉星, 王琳, 等. 海洋立管两相流动及管道振动特性试验研究[J]. 石油机械, 2016, 44(4): 46–50. |
| [14] | 陈志华. MSC Adams多体动力学仿真基础与实例解析[M]. 北京: 中国水利水电出版社, 2012. |
| [15] | 胡家顺, 冯新, 周晶. 考虑边界土体性质悬跨管道振动特性分析[J]. 大连理工大学学报, 2010, 50(3): 409–415. DOI: 10.7511/dllgxb201003017 |



