0 引言
目前,对流固耦合问题关注的重点主要是结构的安全问题,在结构设计和可靠运行上取得了许多有益的成果[1-3],在流固耦合计算分析方面积累了经验[4-6]。但对于一些流体设备而言,流体与结构的相互作用对其内部流体流动状态及工作性能的影响则是更值得关注的问题,如振动耦合效应下水力旋流器内两相流动就属于这类问题。
袁寿其等研究发现了考虑流固耦合作用后叶轮流道内流动的不对称性。刘莹等[7]分析认为双向流固耦合模型更符合描述真实的血液流动情况。
刘杨和何金朋为提高旋流器分离性能提出了建议和方法。K.U.BHASKAR等[8]的研究结果表明:雷诺应力模型模拟结果与试验测试结果的误差最小。王尊策等[9]研究得到了旋转壁面运动对切向速度、轴向速度和径向速度等分布规律的影响;Y.R.MURTHY等[10]研究发现RSM模型预测的流场合理;文献[11]采用RSM模型对耦合效应下变径圆管内单相流体的流动进行了预测分析。
但针对旋流器结构的振动及振动条件下流场流动规律的研究较少。为使水力旋流器在工程上得到更合理的应用,有必要进一步研究振动耦合效应下水力旋流器油水两相流动特点,揭示振动耦合效应下两相流场变化对旋流器工作性能的影响,以期为旋流器的设计和应用提供理论依据。
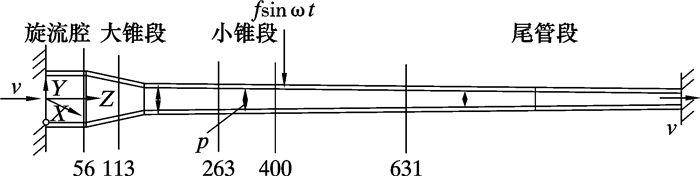
1 流固耦合力学模型与模拟方法 1.1 水力旋流器流固耦合力学模型研究对象为主直径28 mm的典型双锥结构水力旋流器。旋流器工作时,两端圆管截面为固定约束,考虑旋流器结构外壁面局部受到周期的激振作用,内壁面与内流体交界面为流固耦合界面,旋流器固体结构与管内螺旋湍流构成一个流固耦合系统。其力学模型如图 1所示。
|
| 图 1 水力旋流器流固耦合力学模型 Fig.1 Fluid-solid coupling mechanics model of hydrocyclone |
1.2 数值模拟方法 1.2.1 油水两相流控制方程
在水力旋流器内流体微元体应满足两相质量守恒和动量守恒,两相流模型采用混合模型。
油水混合两相流模型的连续性方程为:

|
(1) |
油水混合两相流模型的动量方程:
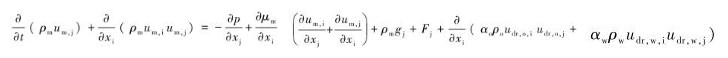
|
(2) |
油相体积分数方程为:

|
(3) |
式中:ρm为混合密度,kg/m3,ρm=αoρo+αwρw;m, iu为质量平均速度,m/s,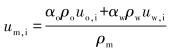
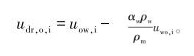
在对水力旋流器进行流固耦合分析时,只有考虑结构在内力和外力共同作用下的振动情况,才能更好地确定结构振动对流体流动的影响。结构的运动方程为:

|
(4) |
式中:[M]为质量矩阵;[C]为阻尼矩阵;{Ff}为流体对结构的载荷;{Fo}为外界随时间变化的载荷;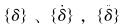
水力旋流器的主直径28 mm,溢流口直径8 mm。为了考察各截面的速度分布、压力分布及湍流强度等流动特性,分别在旋流腔与大锥交界处、大锥段、小锥段和尾管段取5个截面(Z=56、113、263、400和631 mm)进行分析,Z轴正方向为流动方向。
流体部分采用水和油两相混合介质,其密度分别为998.2和889.0 kg/m3,黏度分别为1.03和5.0 mPa·s。水力旋流器固体域采用钢材,密度为7.8×103 kg/m3,弹性模量为200 GPa,泊松比为0.3。
采用雷诺应力的湍流模型对流体控制方程封闭,基于有限体积法对流体域控制方程离散。入口边界采用质量入口,总处理量为4 m3/h,油相体积分数为1%。底流、溢流出口边界考虑充分发展条件,设分流比为10%,壁面按照无滑移壁面条件处理,激振力和激振频率分别为10 N和17.5 Hz,激振力沿Y轴方向施加,激振位置为小锥段中间,激振面投影长度80 mm,旋流器钢材两端采用固定约束。
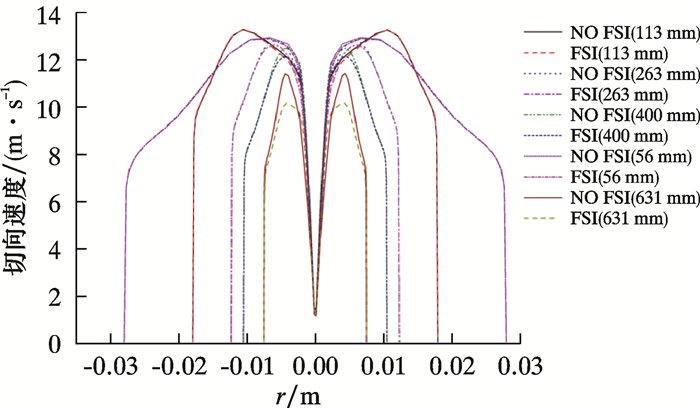
2 结果与分析为了研究振动耦合作用对水力旋流器流场的影响,分别计算了非耦合(NO FSI)和周期振动耦合(FSI)作用下的流场,并进行了比对分析。水力旋流器的速度场考察主要在切向速度、轴向速度与径向速度3个分量展开,切向速度在3个速度分量中数值最大,是油水两相离心分离的重要因素。图 2给出了耦合与非耦合条件下,旋流器不同截面位置的切向速度分布。r为旋流器直径的位置。从图可以看出,二者切向速度的整体分布趋势相近,但在切向速度峰值区域附近,与非耦合的切向速度相比,耦合条件下的切向速度沿管流方向逐渐降低,二者之间最大差值约1.45 m/s。沿流动方向,耦合条件下切向速度在截面上分布对称性降低。图 3给出了耦合条件下X轴、Y轴方向及非耦合条件下Z=631 mm截面的切向速度分布。从图可以看出,受周期激振力及耦合效应的影响,X轴方向的切向速度在峰值区域明显大于Y轴方向的切向速度,这是因为Y轴方向激振造成的管壁运动增大了X轴方向流体的剪切作用。
|
| 图 2 耦合与非耦合条件下不同截面切向速度分布 Fig.2 Tangential velocity distribution of different cross sections with/without coupling |

|
| 图 3 Z=631 mm截面X轴和Y轴切向速度分布 Fig.3 Tangential velocity distribution of X, Y axis on Z=631 mm cross section |
图 4给出了耦合与非耦合条件下,旋流器不同截面位置的轴向速度分布。从图可以看出,2种条件下轴向速度的整体分布趋势相近,但耦合条件下轴向速度的绝对值在Z=400 mm之前的截面,中心区域均低于非耦合条件,且二者之间最大差值约0.75 m/s。图 5给出了耦合条件下X轴、Y轴方向及非耦合条件下Z=631 mm截面的轴向速度分布。从图可以看出,受周期激振力及耦合效应影响,X轴与Y轴方向的轴向速度变化较小,说明轴向速度受激振力的影响较小。

|
| 图 4 耦合与非耦合条件下不同截面轴向速度分布 Fig.4 Axial velocity distribution of different cross sections with/without coupling |

|
| 图 5 Z=631 mm截面X轴和Y轴轴向速度分布 Fig.5 Axial velocity distribution of X, Y axis on Z=631 mm cross section |
图 6给出了耦合与非耦合条件下,旋流器不同截面位置的径向速度分布。从图可以看出,在Z=400 mm之前的截面,2种条件下径向速度分布的整体趋势相近,在Z=400 mm之后截面2种条件下的径向速度分布趋势完全不同,受激振力及耦合效应的影响,流体的径向速度方向指向中心区域,但是在Z=400 mm之后的截面上,轴向速度的运行方向朝向尾管,对旋流器的分离性能没有影响。图 7给出了耦合条件下X轴、Y轴方向及非耦合条件下Z=631 mm截面的径向速度分布。从图可以看出,X轴与Y轴方向的径向速度呈相反的态势,说明受周期振动影响,流体在同一截面径向速度方向存在差异,即同一截面不同的坐标方向,径向速度有的指向中心、有的指向壁面,这对水力旋流器的油水分离不利。

|
| 图 6 耦合与非耦合条件下不同截面径向速度分布 Fig.6 Radial velocity distribution of different cross sections with/without coupling |

|
| 图 7 Z=631 mm截面X轴和Y轴径向速度分布 Fig.7 Radial velocity distribution of X, Y axis on Z=631 mm cross section |
图 8给出了耦合与非耦合条件下旋流器不同截面位置的压力分布。从图可以看出,2种条件下各截面压力分布的整体趋势相近,只有在中心区域耦合条件下的压力均大于非耦合条件下的压力。

|
| 图 8 耦合与非耦合条件下不同截面压力分布 Fig.8 Pressure distribution of different cross sections with/without coupling |
图 9~图 11给出了1个振动周期T内Z=631 mm截面上切向速度、轴向速度与径向速度分布。从图可以看出,3种速度都出现了随时间梯度变化的现象,但切向速度与轴向速度变化不大,径向速度变化最大,甚至出现了速度正负交错的现象,这对旋流器的油水分离不利。

|
| 图 9 不同时刻Z=631 mm截面耦合条件下切向速度分布 Fig.9 Tangential velocity distribution on Z=631 mm cross section with coupling at different times |

|
| 图 10 不同时刻Z=631 mm截面耦合条件下轴向速度分布 Fig.10 Axial velocity distribution on Z=631 mm cross section with coupling at different times |

|
| 图 11 不同时刻Z=631 mm截面耦合条件下径向速度分布 Fig.11 Radial velocity distribution on Z=631 mm cross section with coupling at different times |
为进一步了解耦合与非耦合条件对水力旋流器分离性能影响,分别给出了油相的滑移速度与质量分数分布图,如图 12和图 13所示。从图 12可以看出,在距离入口较近的截面,2种条件下的油相滑移速度差别较小,只在轴心处非耦合的油相滑移速度略大;受激振力的影响,截面Z=263 mm后的近壁侧,耦合条件下的油相滑移速度大于非耦合的油相滑移速度。从图 13可以看出,振动耦合条件下的油相质量分数均大于非耦合条件下的油相质量分数,这对油水两相分离十分有利。但结合速度场可知,在旋流器的后端,耦合条件下的径向速度出现交错现象,同时在轴心处耦合条件的轴向速度也小于非耦合条件的轴向速度,以及耦合条件下的切向速度衰减,这些都是影响油水两相分离的不利因素;另外,从分离效率看,受激振作用的旋流器分离效率较低,二者之差约为3.2%。通过以上分析可以看出,激振力对水力旋流器的流场和分离性能均产生影响,这在今后的工程应用中需要重点考虑。

|
| 图 12 耦合与非耦合条件下不同截面油相滑移速度分布 Fig.12 Slip velocity distribution of oil phase on different cross sections with/without coupling |

|
| 图 13 耦合与非耦合条件下不同截面油相质量分数分布 Fig.13 Oil phase mass fraction distribution on different cross sections with/without coupling |
3 结论
(1) 振动耦合效应的影响使得切向速度沿流动方向逐渐衰减,耦合条件下的切向速度低于非耦合条件下的切向速度,二者之间最大差值约1.45 m/s,且出现了激振方向与非激振方向流场不对称的特点。
(2) 轴向速度受激振力影响较小,在激振位置之后,耦合与非耦合条件下的径向速度差异逐渐增大,且不同时刻径向速度变化趋势明显。
(3) 受激振力的影响,耦合条件下的油相滑移速度在近壁侧增大,特别在Z=400 mm之后截面逐渐明显。耦合条件下轴心的油相质量分数大于非耦合条件下的油相质量分数,但振动耦合条件下的分离效率低于非耦合条件下的分离效率,二者差值约为3.2%。
| [1] | 王琳, 匡友弟, 黄玉盈, 等. 输液管振动与稳定性研究的新进展:从宏观尺度到微纳米尺度[J]. 固体力学学报, 2010, 31(5): 481–495. |
| [2] | 黄益民, 刘伟, 刘永寿, 等. 充液管道模态的参数灵敏度及其共振可靠性分析[J]. 振动与冲击, 2010, 29(1): 193–195. |
| [3] | 梁军, 朱庆杰, 苏幼坡. 流固耦合作用下流体对管道抗震性能的影响分析[J]. 世界地震工程, 2007, 23(3): 23–28. |
| [4] | 冯志鹏, 臧峰刚, 张毅雄. 三维横向流体诱发直管振动的数值模拟[J]. 应用数学和力学, 2013, 34(12): 1311–1320. DOI: 10.3879/j.issn.1000-0887.2013.12.010 |
| [5] | LE TALLEC P, MANI S. Numerical analysis of a linearised fluid-structure interaction problem[J]. Numer. Math., 2000, 87(2): 317–354. DOI: 10.1007/s002110000183 |
| [6] | PELLICANO F, AMABILI M, PAIDOUSSIS M P. Effect of the geometry on the non-linear vibration of circular cylindrical shells[J]. International Journal of Non-Linear Mechanics, 2002, 37(7): 1181–1198. DOI: 10.1016/S0020-7462(01)00139-1 |
| [7] | 刘莹, 张伟中, 殷艳飞, 等. 双向流固耦合作用下狭窄左冠状动脉内两相血流分析[J]. 应用数学和力学, 2016, 37(5): 501–509. DOI: 10.3879/j.issn.1000-0887.2016.05.006 |
| [8] | BHASKAR K U, MURTHY Y R, RAJU M R, et al. CFD simulation and experimental validation studies on hydrocyclone[J]. Minerals Engineering, 2007, 20(1): 60–71. DOI: 10.1016/j.mineng.2006.04.012 |
| [9] | 王尊策, 张井龙, 孔令真, 等. 绕轴旋转旋流分离器内流场的数值模拟[J]. 哈尔滨工业大学学报, 2011(增刊1): 126–130. |
| [10] | MURTHY Y R, BHASKAR K U. Parametric CFD studies on hydrocyclone[J]. Powder Technology, 2012, 230: 36–47. DOI: 10.1016/j.powtec.2012.06.048 |
| [11] | 李森, 张健, 王尊策, 等. 流固耦合作用下水力旋流器内流场的数值模拟[J]. 化工机械, 2015, 42(5): 706–710. |



