2. 中国石油新疆油田公司石西油田作业区;
3. 中国石化中原石油工程有限公司
2. Shixi Oilfield Operation Area of PetroChina Xinjiang Oilfield Company;
3. Sinopec Zhongyuan Petroleum Engineering Co., Ltd
0 引言
抽油杆柱是连接井下抽油泵和井口抽油机的杆柱组合,是有杆抽油系统中重要的传递环节。在生产过程中,由于交变载荷、井眼轨迹、地层流体、温度和压力等因素的影响,使得杆柱工作状况恶劣,易发生磨损,形成管杆偏磨,严重的可导致偏磨断脱,缩短检泵周期,增加油田的生产成本。
针对杆柱磨损,现今常用的分析方法主要有杆柱磨损量计算和管杆偏磨区域预测[1-5]。磨损量计算是基于摩擦力学模型进行杆柱磨损量计算,适用于已发生偏磨和井况较为简单的抽油井,对于井下情况复杂的抽油杆柱,不能全面地分析其磨损情况。偏磨区域预测是通过杆柱受力和屈曲方程进行分析计算,但是对于杆柱磨损程度无法进行判断。杆柱使用寿命方面,传统的计算方法通过预测磨损量来计算杆柱的疲劳极限[6-7],没有考虑到井下复杂情况以及预测参数的不确定性,计算结果不能很好地反映杆柱工况以及安全性。
支持向量机(SVM)对于高维度小样本数据具有很好的拟合效果,适用于井下情况较为复杂的管杆偏磨分析;同时,遗传算法(GA)可以提高支持向量机的预测精度,从而提升管杆磨损量计算的准确性。蒙特卡洛模拟计算可以有效地解决复杂函数关系下的概率问题,适用于影响因素多、关系复杂的杆柱强度校核与安全性分析。因此,笔者采用GA-SVM进行杆柱磨损分析,建立影响因素与磨损率的映射关系,实现抽油杆柱偏磨区域和程度的判别。充分考虑井下工程参数的不确定性,结合蒙特卡洛模拟法对杆柱使用过程中的安全性进行评价,并根据安全可靠程度实现抽油杆柱寿命计算。
1 抽油杆柱受力分析 1.1 抽油杆柱侧向支撑力计算无论是直井还是定向井,由于钻井过程中的地质因素(地层倾斜)和工程因素(钻柱弯曲)的影响,使得井眼具有三维曲线特性[8]。由于井眼的弯曲,使得抽油杆柱上、下运动时势必会与油管内壁发生接触,形成侧向支撑力,进而造成管杆之间的磨损。侧向支撑力[9]计算公式为:
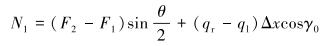
|
(1) |
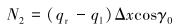
|
(2) |
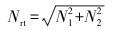
|
(3) |
式中:N1为与狗腿平面平行的支撑力,N;N2为与狗腿平面垂直的支撑力,N;F1为测量段近井口一端的轴向载荷,N;F2为测量段近井底一端的轴向载荷,N;Δx为测量点跨度,m;qr为单位长度抽油杆所受重力,N/m;ql为单位长度抽油杆所受浮力,N/m;θ为井段狗腿角,(°);γ0为井身曲线主法线方向与重力矢量之间的夹角,(°);Nrt为侧向支撑力,N。
1.2 抽油杆柱轴向载荷计算抽油杆柱受力主要包括杆柱分布力和泵端局部力[10-11]。对于杆柱分布力,主要由抽油杆柱自重、杆柱与液体的摩擦力、杆柱与油管内壁的摩擦力和惯性力组成。计算公式为:
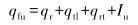
|
(4) |
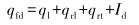
|
(5) |
式中:qfu、qfd分别为上冲程和下冲程时单位长度抽油杆受力,N;qtl为单位长度液体与油管之间的摩擦力,N;qrt为单位长度的抽油杆与油管之间的摩擦力,N;qrl为单位长度的抽油杆与液柱之间的摩擦力,N;Iu为上冲程时单位长度抽油杆和液柱所产生的惯性载荷,N;Id为下冲程时单位长度抽油杆所产生的惯性载荷,N。
对于泵端局部力,主要由活塞与泵筒摩擦力、游动阀液流阻力、液柱载荷以及井口回压组成,计算公式为:
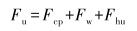
|
(6) |
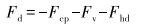
|
(7) |
式中:Fu、Fd分别为上冲程和下冲程时泵端局部力,N;Fcp为柱塞与衬套之间的摩擦力,N;Fv为流体经过游动阀的液流阻力,N;Fw为液柱载荷,N;Fhu、Fhd分别为上冲程和下冲程时井口回压作用于活塞上的力,N。
将抽油杆柱划分为若干单元,根据上面的计算公式,以泵端为起始点,进行自下而上的逐单元计算,由于轴向载荷与侧向支撑力之间存在影响关系,所以采用试算迭代的方法进行处理,最后可获得抽油杆柱上、下冲程时的轴向载荷分布与侧向支撑力分布。
2 抽油杆柱磨损分析与安全性评价 2.1 抽油杆柱磨损分析在实际生产过程中,抽油杆柱通过往复运动,将油管内的油水抽出。抽油杆柱在运动过程中,会受到来自于井眼轨迹、轴向载荷、流体性质、压力和温度等多方面因素的影响,使其发生偏磨,造成杆柱磨损[12-13]。因此,选取GA-SVM模型进行抽油杆柱磨损分析。
GA-SVM模型,即基于遗传算法优化的支持向量机模型,对于高维数和小样本的分析数据,具有很好适应性,可以建立影响因素与杆柱磨损率之间的映射关系,进而实现抽油杆柱的磨损分析。具体分析步骤[14-15]如下:
(1) 选取轴向最大载荷、轴向最小载荷、侧向支撑力、抽油杆尺寸、油管内径、含水率、温度、压力和扶正间距作为输入数据,即[x1,x2,x3,x4,x5,x6,x7,x8,x9]。抽油杆柱磨损率为输出数据,即[y]。
(2) 通过查阅检泵资料,获得现场偏磨数据,建立输入和输出的学习样本。
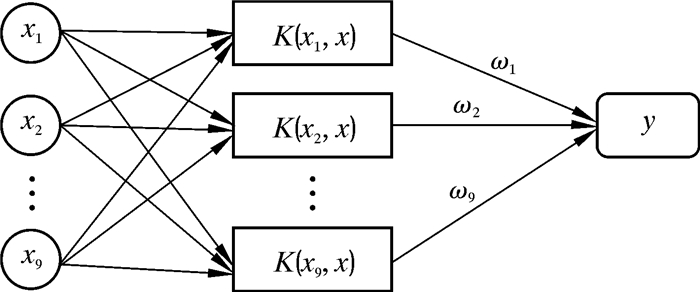
(3) 将输入数据代入SVM模型的输入层,输出数据代入输出层,SVM模型通过核函数K(xn, x)将样本数据投射到特征空间(维度比样本高)内,通过调节权值ω求出样本的最有分类平面,从而获得输入与输出的映射关系,具体结构如图 1所示。
|
| 图 1 SVM模型结构图 Fig.1 Structure diagram of SVM model |
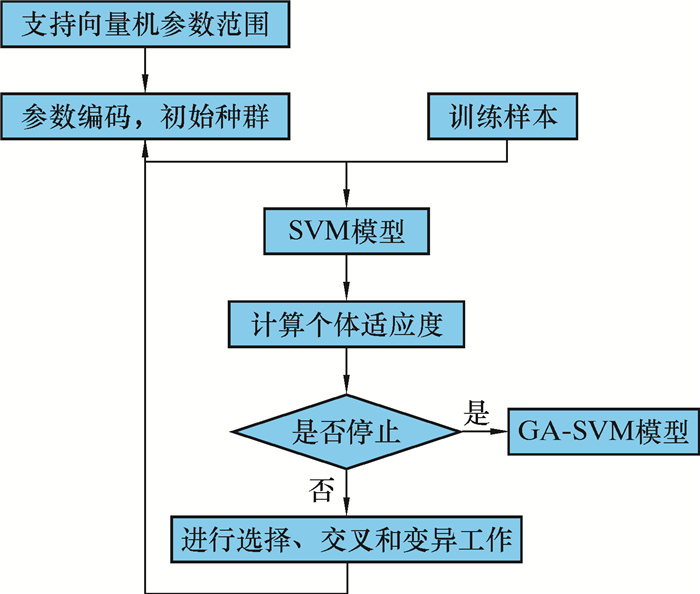
(4) 通过遗传算法(GA),对核函数中的参数进行优化迭代,获得最优的参数组合,进而提高SVM模型的预测精度,迭代流程如图 2所示。
|
| 图 2 GA-SVM模型流程图 Fig.2 Flow chart of GA-SVM model |
最终,构建出井下影响因素与杆柱磨损率之间的映射关系,形成磨损率的预测模型,进而实现抽油杆柱的磨损分析。
2.2 抽油杆柱安全性评价抽油杆柱磨损之后,其直径会缩小,内部应力也会发生,进而影响抽油杆柱工作过程中的安全性,因此,需要对杆柱磨损后的安全可靠性进行评价。
对于抽油杆柱磨损面积的确定,一般认为杆柱磨损均匀,即抽油杆柱磨损面为杆柱与油管相交的月牙面。因此,抽油杆柱磨损面积与磨损量之间的关系为[16]:
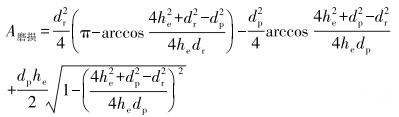
|
(8) |
式中:dr为抽油杆半径,m;he为抽油杆与油管的中心距,m;dp为油管内半径,m。
由于井下工作环境复杂,影响因素较多,测试数据以及理论计算数据与实际情况之间存在一定的差异,造成抽油杆柱磨损量分析也存在一定误差,所以充分考虑井下参数的不确定性,结合概率统计学,对抽油杆柱的安全性进行评价。由于GA-SVM构造的数学模型结构较为复杂,并且存在维数转换,无法利用传统的概率计算进行处理,所以笔者采用蒙特卡洛模拟法进行可靠程度的计算[17]。评价步骤如下。
(1) 结合现场实际工况,根据井下参数的自身概率分布,进行随机选取,假设随机模拟N次,构造出随机输入矩阵为:

|
(2) 将随机输入矩阵代入已建立的抽油杆柱磨损分析GA-SVM模型中,获得杆柱磨损率的输出数组[y1 y2……yN],根据抽油杆柱往复运动次数,计算出杆柱磨损量数组[h1 h2……hN]。
(3) 将磨损量数组代入磨损面积计算公式,获得磨损面积数组[A1 A2……AN]。
(4) 磨损面积数组确定后,计算出磨损后剩余截面上的最大应力和最小应力数组分别为[σ11 σ12……σ1N]和[σ21 σ22……σ2N],再根据修正API准则[18],计算出最大许用应力数组。对最大应力数组和最大许用应力数组进行对比统计,最大应力小于最大许用应力的数据个数为Ns,则该段杆柱的安全可靠程度为:
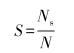
|
(9) |
通过与现场资料对比分析,可靠程度可划分为4个等级:安全、较安全、较危险和危险。对于可靠程度处于安全与较安全等级的抽油杆柱,基本没有强度破坏风险,可继续工作;对于处于较危险等级的抽油杆柱,存在一定的安全风险,可根据其寿命进行判断;对于处于危险等级的抽油杆柱,必须提出杆柱进行处理,防止发生杆柱断脱。各类等级区间如表 1所示。
根据安全等级可以确定出抽油杆柱运行过程中的安全性,随着杆柱的往复运动,磨损会逐渐加剧,安全等级会随之降低,当安全等级降至危险区域时,杆柱则不能继续使用。因此,可以根据以下公式进行寿命计算。
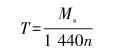
|
(10) |
式中:T为抽油杆柱寿命,d;Ms为安全可靠程度为20%时的杆柱往复运动次数;n为冲次,min-1。
3 实例分析 3.1 训练样本与磨损分析模型建立选取新疆油田石南区块生产井进行计算分析。通过对生产参数、杆柱组合、井眼轨迹参数以及检泵资料归纳统计,建立抽油杆柱磨损分析的样本数据,部分数据如表 2所示。
| 最大载荷/ kN |
最小载荷/ kN |
侧向支撑 力/N |
抽油杆直 径/mm |
油管内径/ mm |
含水质量 分数/% |
温度/℃ | 压力/MPa | 扶正器间 距/m |
每次磨损率/ (10-5 mm) |
| 22.5 | -0.2 | 120 | 19 | 62 | 88 | 48 | 18 | 5 | 1.2 |
| 34.8 | 14.1 | 285 | 22 | 62 | 74 | 29 | 11 | 9 | 0.8 |
| 18.2 | -6.8 | 187 | 19 | 62 | 79 | 49 | 18 | 3 | 1.4 |
| 15.2 | -6.3 | 223 | 19 | 62 | 85 | 49 | 22 | 3 | 1.2 |
| 11.5 | -7.9 | 177 | 19 | 62 | 83 | 51 | 23 | 5 | 1.9 |
| 29.8 | 5.7 | 244 | 22 | 62 | 83 | 33 | 15 | 9 | 1.2 |
| 57.2 | 32.5 | 482 | 25 | 75 | 76 | 20 | 8 | 9 | 1.3 |
| 25.4 | -1.5 | 72 | 19 | 62 | 92 | 46 | 16 | 5 | 0.9 |
| 17.3 | -6.1 | 113 | 19 | 62 | 90 | 50 | 21 | 2 | 0.3 |
| 19.6 | -4.4 | 197 | 19 | 62 | 81 | 49 | 17 | 2 | 0.1 |
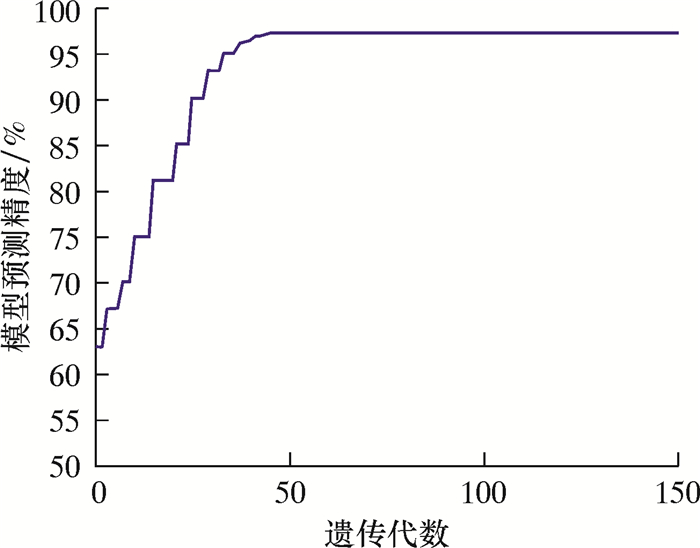
利用支持向量机模型,对样本数据进行学习,并通过遗传算法,不断迭代优化支持向量机核函数,最终获得最优的抽油杆柱磨损分析模型,预测精度随遗传优化代数变化曲线如图 3所示。由图可知,构造的GA-SVM模型预测精度为97%,满足杆柱磨损分析的需要。
|
| 图 3 预测精度随遗传优化代数变化曲线 Fig.3 Effect of genetic optimization algebra on predictive accuracy |
3.2 抽油杆柱安全可靠程度计算
选取该区块内A井,进行抽油杆柱安全性评价。通过对比分析现场载荷、井眼轨迹、温度以及压力的计算数值与实际数值之间的误差,以上这些参数的数据分布基本满足正态分布。对于杆柱尺寸、油管内径以及扶正间距则为固定值,可看作方差为0的正态分布,各类输入参数的方差数据如表 3所示。
| 输入 参数 |
最大载荷/ kN |
最小载荷/ kN |
侧向支撑 力/N |
抽油杆直 径/mm |
油管内径/ mm |
含水质量 分数/% |
温度/ ℃ |
压力/ MPa |
扶正器 间距/m |
安全可靠 程度/% |
安全 等级 |
| 期望 | 31.1 | 8.6 | 200 | 19 | 62 | 81 | 44 | 14 | 9 | 40 | 较危险 |
| 方差 | 3 | 2 | 10 | 0 | 0 | 0 | 2 | 1 |
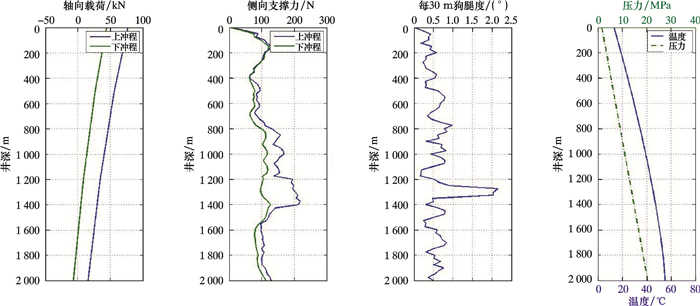
A井为直井,油层中部深度2 550 m,油层温度72 ℃,泵挂深度2 000 m,冲程4.2 m,冲次3 min-1,油压1.6 MPa,套压1.5 MPa,泵径38 mm,油管内径62 mm,活塞与泵筒间隙0.05 mm,含水质量分数81%,原油密度0.78 g/cm3,原油黏度(50 ℃)9.5 mPa·s。根据抽油杆柱轴向载荷、井眼轨迹、侧向支撑力以及温压分布计算公式,可以获得该井轴向载荷、侧向支撑力、井眼狗腿度、温度以及压力的分布曲线,如图 4所示。
|
| 图 4 A井轴向载荷、侧向支撑力、狗腿度、温度和压力分布曲线 Fig.4 Axial load, lateral support force, dogleg angle, temperature and pressure distribution in Well A |
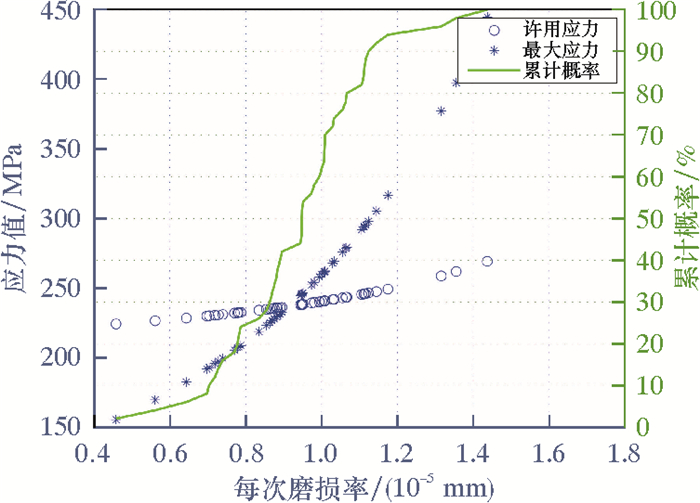
将同一深度下的输入参数,根据其分布形式,随机选取50次,根据安全评价步骤,获得杆柱的安全可靠程度。以井深1 300 m处的资料为例,具体参数如表 3所示。蒙特卡洛模拟结果如图 5所示。相同磨损时间情况下,随着磨损率的增加,最大应力会逐渐超过最大许用应力。通过对蒙特卡洛模拟点的统计,可以看出最大应力小于许用应力的数据点占全部模拟点的40%,即该段抽油杆柱的安全可靠程度为40%。
|
| 图 5 杆柱安全可靠程度蒙特卡洛模拟结果 Fig.5 Monte Carlo simulation results of rod safety and reliability |
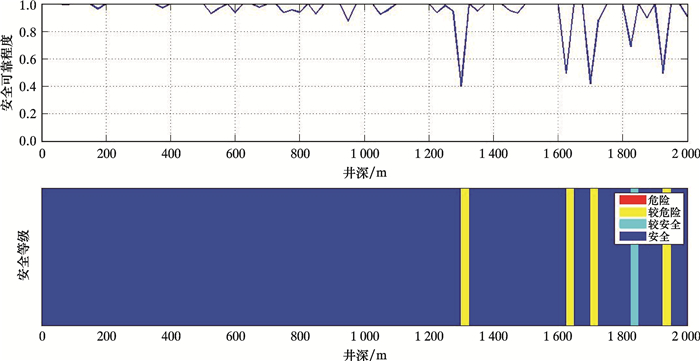
利用同样的方法可以获得全井段的抽油杆柱安全可靠程度,如图 6所示。根据安全等级划分,可将抽油杆柱安全可靠程度分布图转换为安全等级分布图,这样更加便于技术人员识别分析。由图 6可以看出,通过笔者建立的安全评价方法分析,A井抽油杆柱偏磨严重区域主要在1 300和1 700 m处。实际检泵资料中,该井杆柱在1 200~1 300 m和1 600~1 800 m发生严重偏磨,与分析结果基本一致,表明该方法具有一定的现场适用性。
|
| 图 6 A井安全可靠程度与安全等级分布图 Fig.6 Safety and reliability and safety grade distribution in Well A |
3.3 抽油杆柱寿命计算
通过对管杆摩擦次数进行调整,模拟结果为:当摩擦次数达到970 588次时,杆柱的安全可靠程度降至20%,达到危险区域。若抽油机连续运转,A井抽油杆柱的使用寿命为224.7 d,与实际使用时间246 d相差21.3 d,误差为8.7%,这表明该方法具有较好的预测精度。
4 结论与建议(1) 通过GA-SVM建立了井下因素与抽油杆柱磨损率的映射关系,并利用蒙特卡洛模拟法实现了杆柱的安全可靠程度和寿命的计算,从而实现杆柱的磨损分析与安全性评价,分析结果与现场实际情况一致,同时,寿命计算具有较高的预测精度,表明了该方法具有一定的现场适用性。
(2) 该方法可实现全井段的杆柱安全可靠程度与安全等级的计算,通过计算结果可判断出杆柱磨损严重井段和使用寿命,为现场技术人员提供分析处理依据。
(3) 抽油杆柱井下受力与工作环境是影响其安全可靠程度的重要因素,因此建议对其进一步分析研究,以提高杆柱安全分析与寿命预测的精度。
| [1] | 杨海滨, 狄勤丰, 王文昌. 抽油杆柱与油管偏磨机理及偏磨点位置预测[J]. 石油学报, 2005, 26(2): 100–103. DOI: 10.7623/syxb200502023 |
| [2] | 刘晓旭, 林元华, 曾德智, 等. 有杆抽油系统杆管偏磨磨损量预测研究[J]. 石油矿场机械, 2009, 38(1): 34–37. |
| [3] | 苗长山, 黄源林, 王旱祥. 抽油杆偏磨三维力学模型的建立与分析[J]. 石油机械, 2007, 35(12): 28–31. DOI: 10.3969/j.issn.1001-4578.2007.12.009 |
| [4] | 张江, 孙希庆, 李颖, 等. 史南油田抽杆偏磨断裂原因分析及防治对策[J]. 钻采工艺, 2003, 26(4): 58–62. |
| [5] | 黄伟, 甘床明, 张磊, 等. 基于电参数的螺杆泵杆管偏磨预测研究[J]. 石油钻探技术, 2014, 42(4): 102–106. |
| [6] | 张铁汉. 基于磨损寿命预测的定向井抽油杆柱扶正器配置优化设计[D]. 秦皇岛: 燕山大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10216-1016764560.htm |
| [7] | 丁强. 基于模型的机械设备磨损剩余寿命预测方法的研究[D]. 保定: 河北农业大学, 2001. http://cdmd.cnki.com.cn/Article/CDMD-11920-2001002606.htm |
| [8] | 许涛, 陆正元, 李辉, 等. 抽油机斜直井杆管接触与磨损力学模型[J]. 断块油气田, 2012, 19(1): 124–126. |
| [9] | 王一平, 李明忠, 张玉晓, 等. 定向井抽油杆三维力学模型及在偏磨中的应用[J]. 钻采工艺, 2011, 34(1): 65–68. |
| [10] | 张琪. 采油工程原理与设计[M]. 东营: 石油大学出版社, 2000. |
| [11] | 王文昌, 狄勤丰, 姚建林, 等. 三维定向井抽油杆柱力学特性有限元分析新方法[J]. 石油学报, 2010, 31(6): 1018–1023. DOI: 10.7623/syxb201006026 |
| [12] | 高鹏. H级抽油杆柱力学特性及其设计方法研究[D]. 西安: 西安石油大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10705-1015542544.htm |
| [13] | 张鑫, 张建军, 师俊峰, 等. 基于磨损润滑理论的杆柱寿命预测及多目标优化[J]. 石油机械, 2013, 41(12): 106–111. |
| [14] | 方瑞明. 支持向量机理论及其应用分析[M]. 北京: 中国电力出版社, 2007. |
| [15] | 郭海峰, 李洪奇, 孟照旭, 等. 基于特征选择、遗传算法和支持向量机的水淹层识别方法[J]. 石油天然气学报, 2008, 30(6): 94–99. |
| [16] | 吴延强, 吴晓东, 韩国庆, 等. 基于偏磨分析的杆柱磨损寿命预测模型[J]. 石油钻采工艺, 2013, 35(1): 79–82. |
| [17] | 魏凯, 管志川, 韦杰宏, 等. 基于神经网络和Monte-Carlo模拟的钻井工程风险评估方法[J]. 中国安全科学学报, 2013, 23(2): 123–128. |
| [18] | 林元华, 张德平, 骆发前, 等. 抽油杆疲劳寿命计算研究[J]. 石油钻采工艺, 2005, 27(6): 66–69. |



