2. 合肥通用机械研究所
2. Hefei General Machinery Research Institute
0 引言
水下阀门(如闸阀和球阀等)广泛应用于水下生产设施系统,是保证水下生产系统安全经济运行的重要设备之一。深海球阀主要用于水下生产系统的采油树和管汇等部分,是连接油气管线和其他水下设备的关键设备。深海球阀良好的屈曲稳定性是其在水下作业安全运行的关键。
20世纪中期,T.VON KARMAN等[1]对后屈曲进行了研究,提出了薄壳稳定性理论和载荷-位移非线性对屈曲的作用;为了解释非线性的“跳跃”条件,钱学森提出“等能量准则”[2];后期,不断有人对屈曲理论进行深入研究,如吴洪飞[3]和L.H.DONNELL等[4]研究了初始缺陷对屈曲的影响;周承倜等[5]运用有限差分法和能量法对静水压力作用下的圆柱薄壳进行了屈曲理论分析。V.CARVELLI等[6]通过对潜水器进行研究发现,潜水器下潜工作深度与其外壳所承受的海水外压成正比,当潜水器潜水越深,则其所承受的外压也就越大;杜建科等[7]将理论与数值模拟相结合,在不考虑初始缺陷和非线性的条件下,主要研究壳体内容物体积对均布侧压作用下的圆柱壳屈曲稳定性的影响;陆蓓等[8]运用简化球壳模型对中厚球壳的强度稳定性进行了研究。B.HAN[9]、A.KASAGI[10]和R.A.ARCINIEGA等[11]考虑横向剪切效应和初始几何缺陷等因素对承受外压的复合材料圆柱壳进行了屈曲和后屈曲行为的研究。
现有壳体稳定性研究大多集中于潜水器和船舶等,而作为海洋管线重要节流件的深海球阀的屈曲稳定性还需深入研究。笔者运用ABAQUS有限元数值模拟软件对深海球阀进行屈曲稳定性影响因素分析。研究结果可为其他深海类阀门屈曲稳定性分析提供参考。
1 模型建立 1.1 模型建立利用SolidWorks软件对阀体进行三维建模,运用非线性功能强大的ABAQUS/CAE数值模拟软件对深海球阀进行屈曲分析。首先进行以线弹性模型为基础的线性屈曲分析,将分析结果作为非线性分析的初定初始缺陷,引入初始缺陷.inp文件后进行以弹塑性模型为基础的非线性屈曲分析[12-14]。
将研究对象深海球阀阀体视为外压筒体,设计参数包括DN300、PN120和最大工作深度1 200 m。
从应力角度及网格角度出发,使用与水压试验一致模型,为了更加准确地分析和判断阀体屈曲状态及波数,采用整体阀体模型,导入ABAQUS软件中,模型如图 1所示。
|
| 图 1 深海球阀阀体模型 Fig.1 Model of deep water ball valve |
假设阀体材料为各向同性和理想弹塑性,弹性模量170 GPa,泊松比0.3,屈服强度450 MPa,抗拉强度620 MPa。模型网格划分过程中,采用4节点C3D4网格,网格大小为10×10,节点个数为117 828,单元个数为597 121,网格分布见图 2。

|
| 图 2 深海球阀阀体网格分布图 Fig.2 Grid distribution of deep water ball valve body |
1.2 边界条件处理
球阀启闭状态,假设阀体内、外流体介质参数均不随时间变化,即介质处于定常流动状态。深海球阀在海水中工作时两端会受到管道的刚体位移约束,经过多次计算分析后,选取较为合理的边界条件:对阀体进出口端施加轴向和环向位移约束;施加外部介质载荷po=12.06 MPa(关闭状态);施加内部介质载荷pi=2.06 MPa、外部介质载荷po=12.06 MPa(开启状态)。
2 阀体屈曲稳定性影响因素分析 2.1 有、无内压对阀体屈曲影响通过对启闭状态阀体屈曲稳定性分析可知,不同状态的阀体临界载荷值不同,对仅承受外部载荷与同时承受内、外载荷的阀体进行屈曲研究。线性屈曲分析结果如图 3所示。以初始缺陷0.01t(t为壁厚)为例,得到阀体非线性屈曲载荷-位移曲线图,如图 4所示。
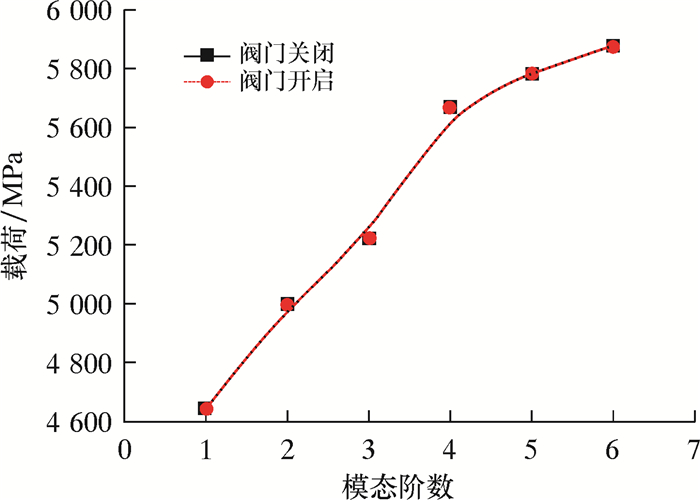
|
| 图 3 阀门开启和关闭时线性临界载荷 Fig.3 Linear critical load on the valve while opened or closed |
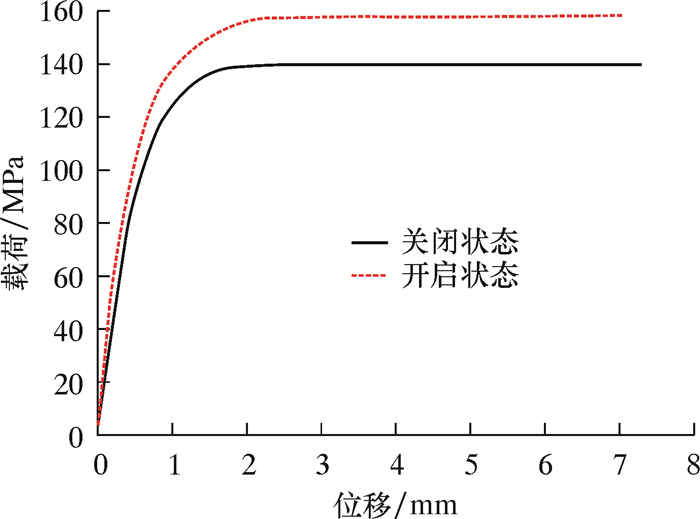
|
| 图 4 阀门开启和关闭时非线性临界载荷 Fig.4 Non-linear critical load on the valve while opened and closed |
由图 3可知,阀门在启闭状态的线性临界载荷值几近相等,以1阶模态为例,当阀处于关闭状态时,即无内部介质压力承受轴向载荷时,阀体线性临界载荷为4 641.6 MPa,当阀处于开启状态时,线性临界载荷为4 641.0 MPa。结果说明线性屈曲载荷值仅仅是壳体本身临界载荷的估计值,与施加载荷的大小无关,是施加载荷的相对大小,可作为预期线性载荷的上限、非线性分析的给定载荷和非线性施加扰动荷载或初始缺陷的依据。
由图 4可知,阀开启状态的非线性临界载荷值大于关闭状态临界载荷值,以初始缺陷0.01t为例,当阀处于关闭状态时,即无内部介质压力时,阀体非线性临界载荷为128.3 MPa,当阀处于开启状态时,非线性临界载荷为144.2 MPa。结果说明内压的存在对阀体的非线性临界载荷有一定影响,当阀体内部存在压力时,内压对壳体产生的拉伸应力抵消了部分外压产生的压缩应力,阀体可承受更大的外压载荷,此时开启状态阀体临界载荷大于关闭状态临界载荷。
2.2 阀杆孔洞对阀体屈曲影响考虑阀体上阀杆孔对阀体屈曲的影响,对完整圆柱、无阀杆阀体和带阀杆阀体进行屈曲研究分析比较,得到关闭状态不同结构对柱壳屈曲的影响(见表 1)。由表可知,阀门关闭状态阀体不同结构形态下的线性屈曲载荷值不同。以完整柱壳为参照对象,当阀体为无阀杆结构时,孔洞的存在使阀体临界载荷值明显下降,当增加阀杆以补偿阀体孔洞缺陷时,壳体线性屈曲载荷明显增大,但阀体无阀杆结构和带阀杆结构的临界载荷值均小于完整柱壳的临界载荷,而阀体孔洞曲率参数决定孔洞对阀体屈曲影响的大小,曲率参数与柱壳半径、圆孔半径有关,当曲率参数越大,对壳体屈曲的影响越大[15]。
| 模态阶数 | 完整圆柱体 | 未带阀杆阀体 | 带阀杆阀体 | |||||
| 屈曲因子 | 弹性失稳力/MPa | 屈曲因子 | 弹性失稳力/MPa | 屈曲因子 | 弹性失稳力/MPa | |||
| 1阶 | 489.4 | 5 872.8 | 386.8 | 4 641.6 | 426.7 | 5 120.4 | ||
| 2阶 | 489.5 | 5 874.0 | 416.4 | 4 996.8 | 430.4 | 5 164.8 | ||
| 3阶 | 547.2 | 6 566.4 | 435.3 | 5 223.6 | 496.9 | 5 962.8 | ||
| 4阶 | 547.2 | 6 566.4 | 472.4 | 5 668.8 | 497.4 | 5 968.8 | ||
| 5阶 | 571.2 | 6 854.4 | 481.9 | 5 782.8 | 579.2 | 6 950.4 | ||
| 6阶 | 571.4 | 6 856.8 | 489.7 | 5 876.4 | 621.6 | 7 459.2 | ||
为了具体了解孔洞对阀体临界载荷的影响,对模型进行非线性分析,引入初始缺陷0.01t,提取最大位移节点处的载荷-位移曲线,如图 5所示。由图 5可知,3种模型的非线性临界载荷值比线性临界载荷值小得多,初始缺陷0.01t时完整圆柱壳体的非线性临界载荷值为163.1 MPa、带阀杆阀体临界载荷值为142.2 MPa、未带阀杆阀体临界载荷值为128.3 MPa,完整圆柱壳的临界载荷值明显大于其他2种结构的临界载荷值,由于阀杆的增加对阀体具有一定的补强作用,故带阀杆阀体临界载荷大于无阀杆阀体临界载荷,这说明孔洞对阀体的屈曲稳定性具有一定的影响,具体影响参数与阀体的壁厚、半径和孔洞半径有关。与线性屈曲结果进行比较,非线性屈曲载荷值小于线性载荷值,这与初始缺陷的大小及施加路径有关。在实际工况中,线性屈曲分析值比较不保守,即阀体在达到线性载荷值之前可能已达到失稳状态。
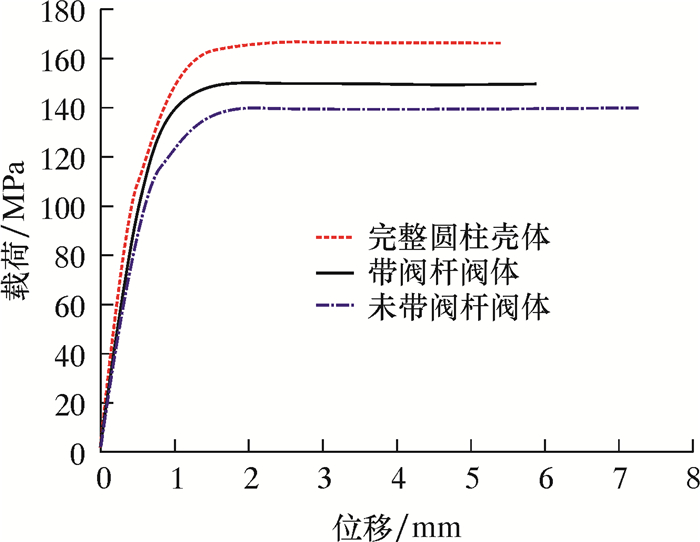
|
| 图 5 3种模型最大位移处载荷-位移曲线 Fig.5 Load-displacement curve at the maximum displacement of the three models |
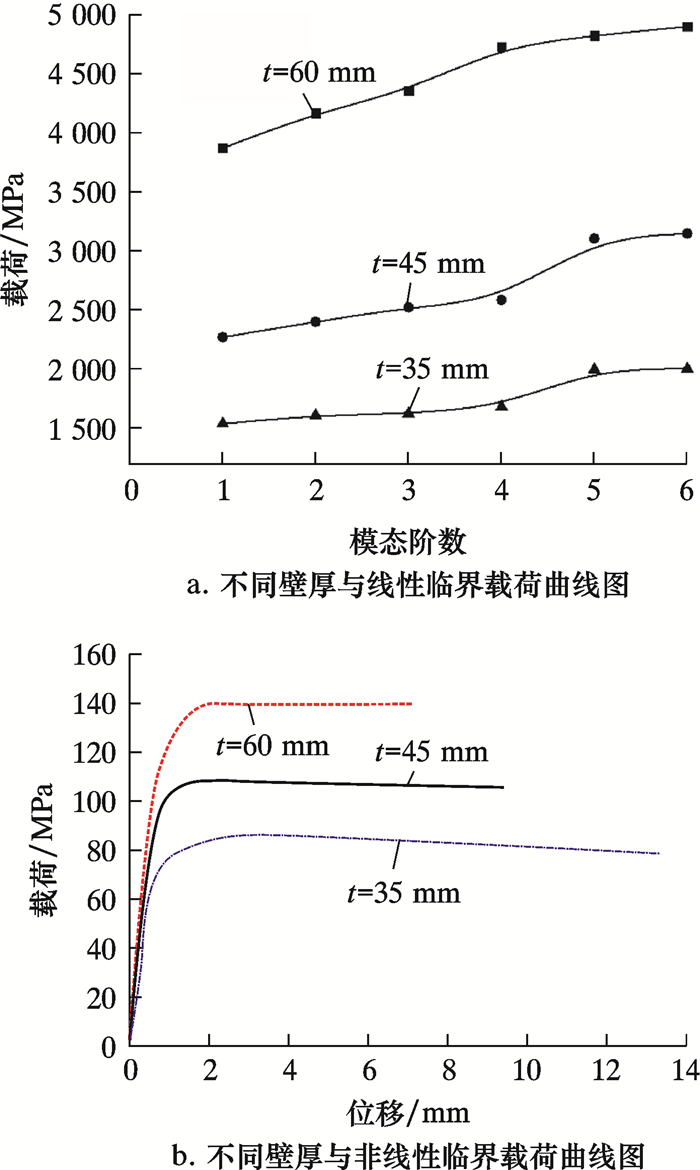
2.3 壁厚对阀体屈曲影响
阀体关闭状态下考虑壁厚对其临界载荷的影响,改变阀体壁厚研究不同壁厚对阀体屈曲的影响,得到不同壁厚阀体线性临界载荷与非线性屈曲的载荷-位移曲线[16-17],如图 6所示。由图可知,壁厚对阀体临界载荷值有较大的影响,随着壁厚的增大,临界载荷值逐渐增大。t=60 mm,非线性临界载荷值为128.3 MPa;t=45 mm,非线性临界载荷值为71.5 MPa;t=35 mm,临界载荷值为67.5 MPa。非线性临界载荷值较为保守,这与初始缺陷的大小和施加路径有关。由图还可看出,非线性临界载荷值随壁厚的增大而增加。
|
| 图 6 不同壁厚与临界载荷曲线图 Fig.6 Critical loads under different wall thickness |
3 结论
(1) 深海球阀启闭状态下阀体的线性临界载荷值几近相等,由于内压对壳体产生的拉伸应力抵消了部分外压产生的压缩应力,故阀体可承受更大的外压载荷。非线性临界载荷值不仅与施加的载荷有关,而且与初始缺陷的大小及施加路径有关。
(2) 阀体上孔洞的存在对阀体可承受载荷和屈曲稳定性有明显的影响。初始缺陷0.01t时完整圆柱壳体、带阀杆阀体和未带阀杆阀体的非线性临界载荷值分别为163.1、142.2和128.3 MPa,阀杆的增加对阀体具有一定的补强作用,故带阀杆阀体临界载荷大于无阀杆阀体临界载荷且小于完整圆柱壳临界载荷。阀体孔洞曲率参数越大,对壳体屈曲的影响越大。非线性屈曲载荷值小于线性载荷值,这与初始缺陷的大小及施加路径有关。
(3) 壁厚对阀体临界载荷值和屈曲稳定性有较大的影响,随着壁厚的增大,临界载荷值逐渐增大。壁厚t=60、45和35 mm时非线性临界载荷值分别为128.3、71.5和67.5 MPa。非线性临界载荷值较为保守,且载荷值随着壁厚的增大而增加。
| [1] | VON KARMAN T, TSIEN H S. The buckling of thin cylindrical shells under axial compression[J]. Journal of Spacecraft and Rockets, 1941(8): 303–312. |
| [2] | TSIEN H S. A theory for the buckling of thin shells[J]. Journal of Spacecraft and Rockets, 1942(9): 373–384. |
| [3] | 吴洪飞, 苑世剑, 王仲仁. 初始缺陷和比例加载路径对圆柱壳弹塑性稳定性的影响[J]. 机械工程学报, 2003, 39(2): 53–57. |
| [4] | DONNELL L H, WAN C C. Effect of imperfections on buckling of thin cylinders and columns under axial compression[J]. Appl. Mech, 1950, 17(1): 73–83. |
| [5] | 周承倜, 周建平. 多层复合材料圆柱壳的非线性失稳计算[J]. 应用数学和力学, 1986, 7(1): 17–23. |
| [6] | CARVELLI V, PANZERI N, POGGI C. Buckling strength of GFRP under-water vehicles[J]. Composite Part:B, 2001, 32: 89–101. DOI: 10.1016/S1359-8368(00)00063-9 |
| [7] | 杜建科, 田晓耕, 沈亚鹏, 等. 复合材料燃烧室均布侧压下稳定性分析[J]. 固体火箭技术, 2002, 25(2): 18–21. |
| [8] | 陆蓓, 刘涛, 崔维成. 深海载人潜水器耐压球壳极限强度研究[J]. 船舶力学, 2004(1): 51–58. |
| [9] | HAN B, SIMITSES G J. Analysis of anisotropic laminated cylindrical shells subjected to destabilizing loads, Part Ⅱ:Numerical results[J]. Composite Structures, 1991, 19: 183–205. DOI: 10.1016/0263-8223(91)90022-Q |
| [10] | KASAGI A, SRIDHARAN S. Imperfection sensitivity of layered composite cylinders[J]. ASCE Journal of Engineering Mechanics, 1995, 121: 810–818. DOI: 10.1061/(ASCE)0733-9399(1995)121:7(810) |
| [11] | ARCINIEGA R A, GONCALVES P B, REDDY J N. Buckling and post buckling analysis of laminated cylindrical shells using third-order shear deformable theory[J]. International Journal of Structural Stability and Dynamics, 2004, 4: 293–312. DOI: 10.1142/S0219455404001240 |
| [12] | 周承倜. 环肋圆柱壳在均匀静水外压力下的弹塑性失稳[J]. 大连工学院学报, 1973(1): 95–125. |
| [13] | 曲文新. 载人潜水器耐压壳结构设计与分析[D]. 哈尔滨: 哈尔滨工程大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10217-1014132662.htm |
| [14] | 龚顺风, 陈源, 金伟良, 等. 高静水压力作用下深海油气管道的局部屈曲[J]. 浙江大学学报(工学版), 2012, 46(1): 14–19. |
| [15] | 郜婕. 圆柱壳结构开孔问题的研究[D]. 哈尔滨: 哈尔滨工程大学, 2005. http://cdmd.cnki.com.cn/article/cdmd-10217-2005137140.htm |
| [16] | 王林. 深海耐压结构型式及稳定性分析[D]. 北京: 中国舰船研究院, 2011. http://cdmd.cnki.com.cn/article/cdmd-10289-1011301502.htm |
| [17] | 袁林. 深海油气管道铺设的非线性屈曲理论分析与数值模拟[D]. 杭州: 浙江大学, 2009. http://cdmd.cnki.com.cn/article/cdmd-10335-2009096522.htm |




