0 引言
目前,浅海钻井平台几乎全部采用了顶驱结构,越来越多的陆地石油钻机也逐步采用了顶驱技术[1]。笔者对交流变频顶驱系统的关键零部件齿轮箱箱体进行了系统分析。齿轮箱实现了电机高速旋转输入低速旋转输出,其中下齿轮箱体是顶驱最重要的承载部件之一,它承受所有钻具的重力及法向载荷,并通过销轴与提环连接[2-4]。程自力等[5]采用COSMOSWorks软件对50DJ型号的顶驱悬挂体进行了强度分析;张洪生等[6]对顶部驱动钻井装置结构选型进行了研究。然而鲜有基于顶部驱动钻井装置的齿轮箱结构优化研究。笔者利用APDL参数化语言对下齿轮箱体开发了完全参数化的有限元计算模型脚本程序,在指定的设计工况下对下齿轮箱体进行强度和刚度的校核,并在此基础上研究侧壁壁厚和底部壁厚对下齿轮箱体结构刚度的影响,所得结论可为下齿轮箱体结构优化设计方案提供数值依据。
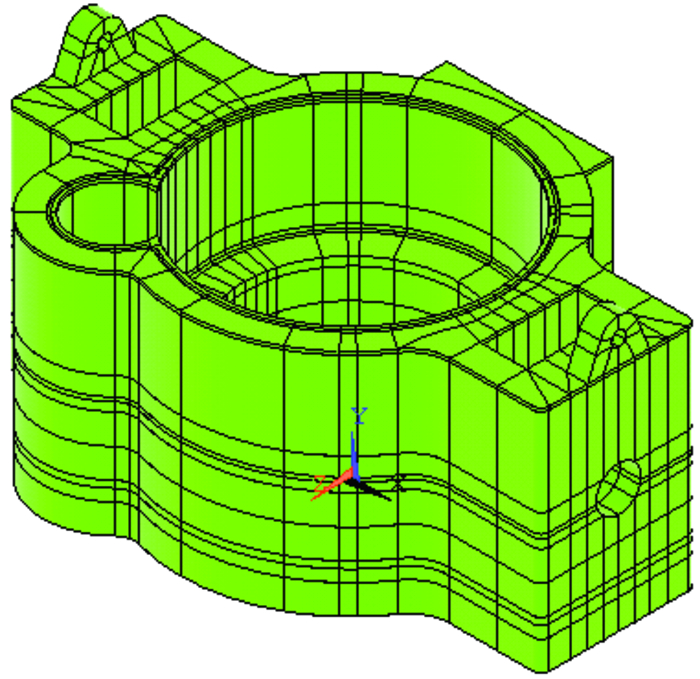
1 下齿轮箱体参数化模型的建立 1.1 参数化几何建模及网格划分应用ANSYS参数化语言APDL对下齿轮箱体进行全参数化几何建模,所有分析模型参数与几何设计模型一一对应。同时,通过设定和调整网格参数,运行开发的程序脚本,生成结构化的有限元网格模型。图 1和图 2给出了下齿轮箱体脚本生成的几何设计模型和有限元网格模型。
|
| 图 1 APDL全参数化建立的几何模型 Fig.1 Geometric model of APDL fully parametric model |
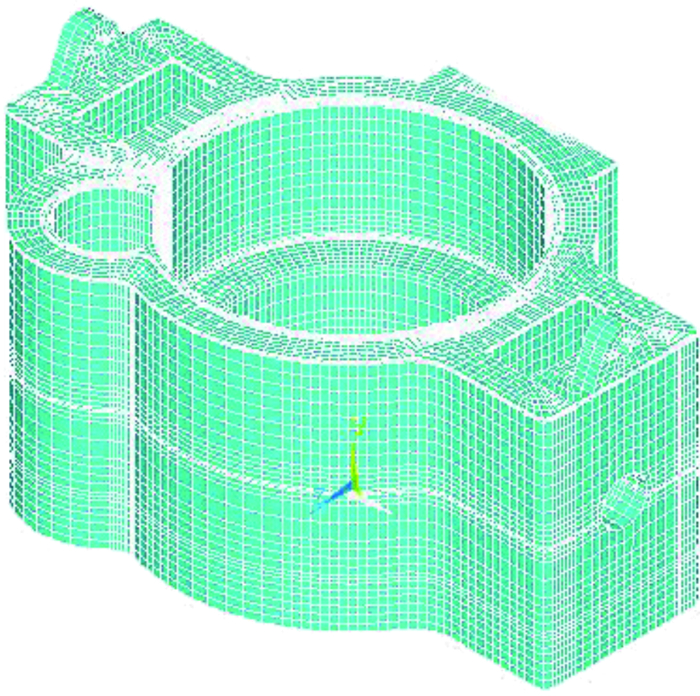
|
| 图 2 APDL全参数化建立的网格模型 Fig.2 Grid of APDL full parametric model |
1.2 材料的选择
该顶驱系统相关结构的设计备选材料20CrMo、35CrMo和42CrMo,根据下齿轮箱体的强度计算结果来选择材料。3种材料的材料属性参数见表 1。从表 1可以看出,3种材料的弹性模量和泊松比接近,对强度校核计算的结果影响可以忽略,因此,在计算中设定材料的弹性模量值为212 GPa,泊松比为0.280。通过计算求解获得的Mises应力值,用来比对各材料的屈服极限,为选取适合的材料提供设计依据。
| 材料 | 弹性模量/GPa | 泊松比 | 屈服极限/MPa |
| 20CrMo | 210 | 0.278 | 685 |
| 35CrMo | 213 | 0.286 | 835 |
| 42CrMo | 212 | 0.280 | 930 |
1.3 载荷和边界条件
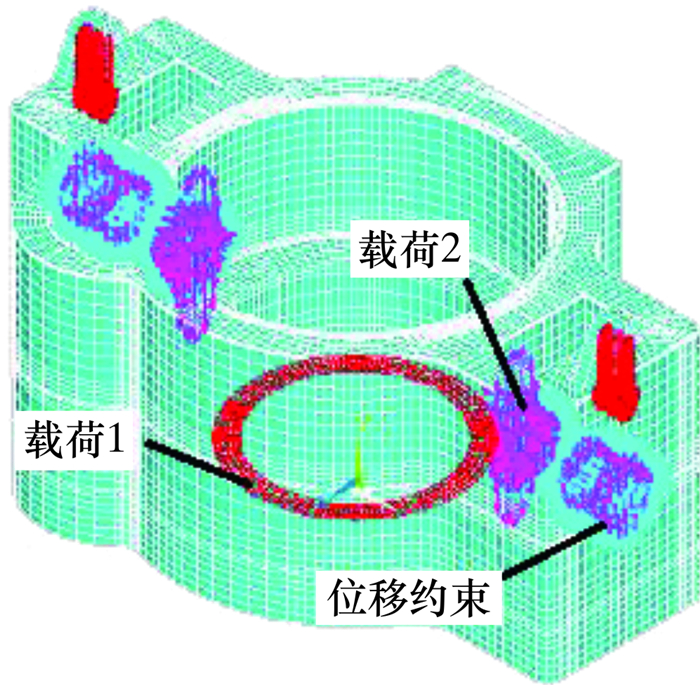
根据下齿轮箱体在整个顶驱系统中的实际受力与约束情况,应用APDL语言定义下齿轮箱体的施加载荷和约束,如图 3所示。考虑到重载和冲击工况的影响,依据SY/T 6726—2008标准,安全系数取为2.73。经核算,强度校核采用的静载荷值为620 kN,对生成的有限元计算模型进行静力学分析。
|
| 图 3 加载后的下齿轮箱体有限元计算模型 Fig.3 Finite element calculation model of the lower gear box after loading |
2 下齿轮箱体强度和刚度的校核 2.1 下齿轮箱体结构变形的数学描述
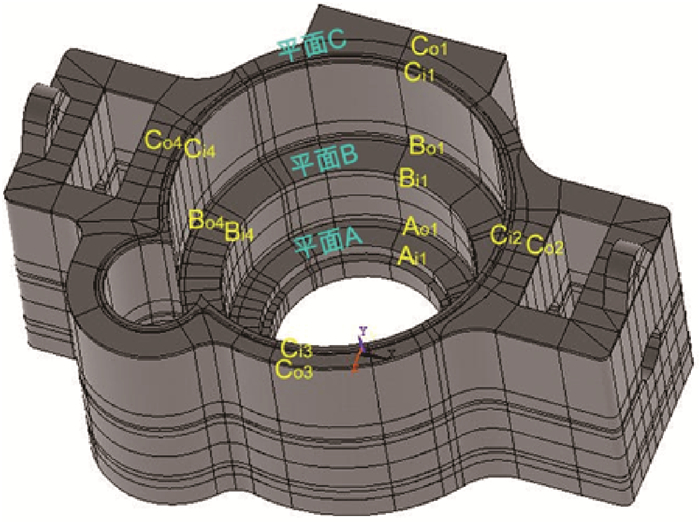
为表征下齿轮箱体的强度和刚度特性,定义平面A、B、C和柱面D、E,如图 4所示。平面A为箱体与主轴承载法兰的水平接触面,柱面D为主轴承载法兰周面和承载轴承周面的周向接触面,水平面B和柱面E分别为主轴齿轮下端面和周面对应的壁面,水平面C为下齿轮箱盖的接合面。上述5个表面在极限载荷条件下的变形程度对下齿轮箱轴系的安全可靠运行有着重要的影响。因此,在满足强度的要求下,通过分析这5个面在极限载荷下的变形程度来描述下齿轮箱体的结构刚度。关键节点的设定如图 5所示,圆环平面A、B、C的内、外环边线与YZ平面和XY平面的交点,沿顺时针方向分别定义为Ai1、Ai2、Ai3、Ai4、Ao1、Ao2、Ao3、Ao4、Bi1、Bi2、Bi3、Bi4、Bo1、Bo2、Bo3、Bo4、Ci1、Ci2、Ci3、Ci4、Co1、Co2、Co3和Co4。

|
| 图 4 下齿轮箱结构示意图 Fig.4 Structural schematic of the lower gear box |
|
| 图 5 关键节点设定示意图 Fig.5 Diagram of key node set |
由相关力学理论定义描述结构强度和刚度的状态参数,依据第四强度理论[7],计算钢材结构件σzs应力(Mises应力)分布,判定处于复杂应力状况下的材料是否进入塑性变形,应满足:
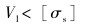
|
(1) |
式中:V1为箱体销轴处最大应力σzs,V1体现箱体的强度特征,[σs]为钢材在单向应力时的屈服极限。
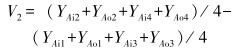
|
(2) |
式中:V2为箱体承载平面(平面A)变形挠度,YAi2为相应节点在Y方向的位移值,其余同理。
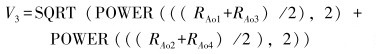
|
(3) |
式中:RAo1、RAo2、RAo3、RAo4为相应节点的径向位移,V3为箱体承载平面(平面A)中心径向位移。
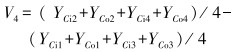
|
(4) |
式中:V4为箱体顶盖平面(平面C)变形挠度。
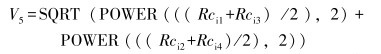
|
(5) |
式中:V5为箱体承载平面(平面C)中心径向位移,RCi1、RCi2、RCi3、RCi4为相应节点的径向位移。
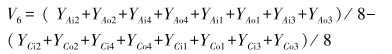
|
(6) |
式中:V6为箱体轴向拉伸变形。
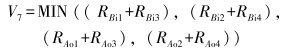
|
(7) |
式中:V7为箱体柱面D收缩变形。
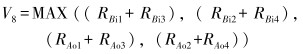
|
(8) |
式中:V8为箱体柱面D扩张变形。
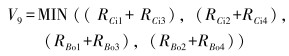
|
(9) |
式中:V9为箱体柱面E收缩变形。
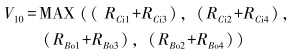
|
(10) |
式中:V10为箱体柱面E扩张变形。
参数V1体现箱体的强度特性,其余参数反映箱体的刚度特性。参数V2、V3、V7、V8定义箱体承载位置(平面A和柱面D)的变形特征,该处变形对主轴承载法兰和承载轴承有直接影响。参数V4、V5、V9、V10定义箱体顶盖位置和主轴齿轮回转空间(平面C和柱面E)的变形特征,该处变形对箱盖和关乎主轴定位的透盖的吻合有直接影响。参数V6反映在载荷作用下箱体的轴向拉伸变形,该透盖变形将对主轴轴系的传动精度产生直接影响。
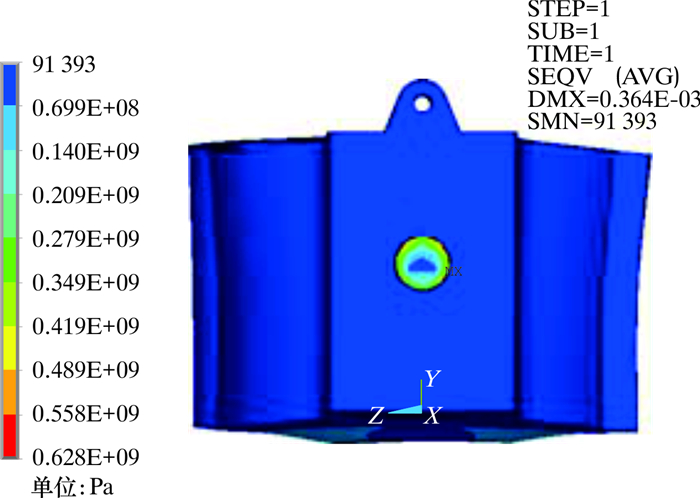
2.2 下齿轮箱体强度校核分析依据行业相关标准及设计要求,考虑冲击工况载荷的影响,实施该型号顶驱机械强度校核的载荷要求为620 kN。由数值计算结果直接得出箱体销轴处最大应力参数V1。应用POST1后处理器,对求解得到的计算结果文件进行后处理,得到结构的应力分布,如图 6和图 7所示。
|
| 图 6 下齿轮箱最大应力位置图 Fig.6 Maximum stress position of the lower gear box |
|
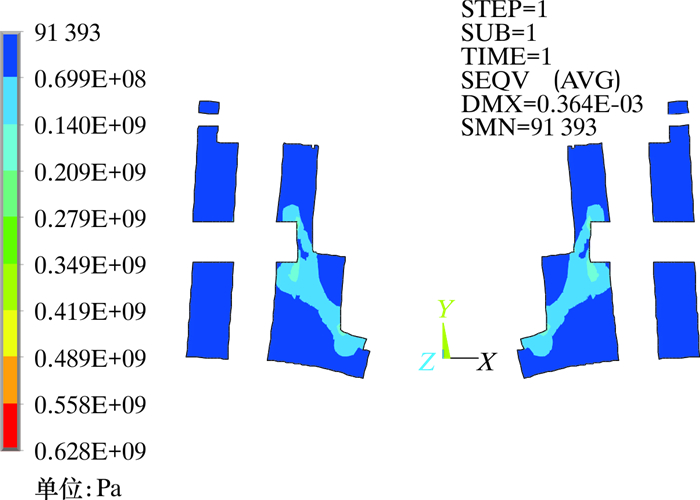
| 图 7 正视剖面(XY)应力分布图 Fig.7 Stress distribution on the front view (XY) |
图 7显示了下齿轮箱体的应力分布情况。由图可知,最大应力位于箱体与提环的销轴接触面,最大应力值为628 MPa,选用35CrMo材料(σs=835 MPa)可以满足结构强度安全设计要求;剖面应力分布显示,箱体与承载法兰接触面斜上50°至销轴孔的带状区域是应力较大区域,在设计与制造环节中应更多考虑。
2.3 下齿轮箱体刚度校核分析应用POST1后处理器,对求解得到的计算结果文件进行后处理,得到下齿轮箱体法向变形图,如图 8和图 9所示。
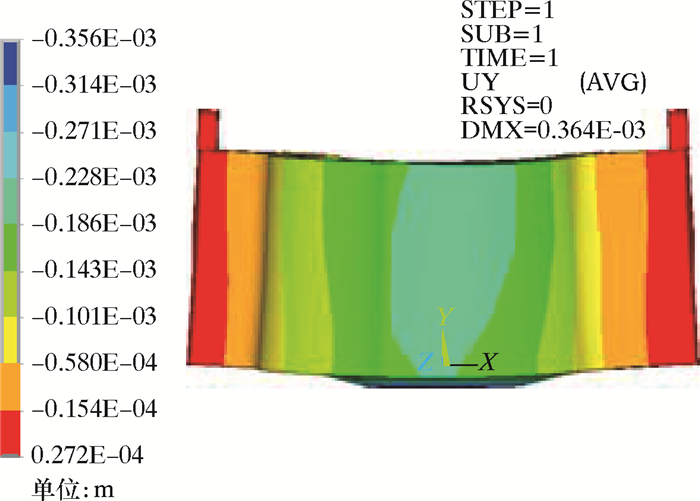
|
| 图 8 下齿轮箱体法向变形正视图 Fig.8 Front view of the normal deformation of the lower gear box |
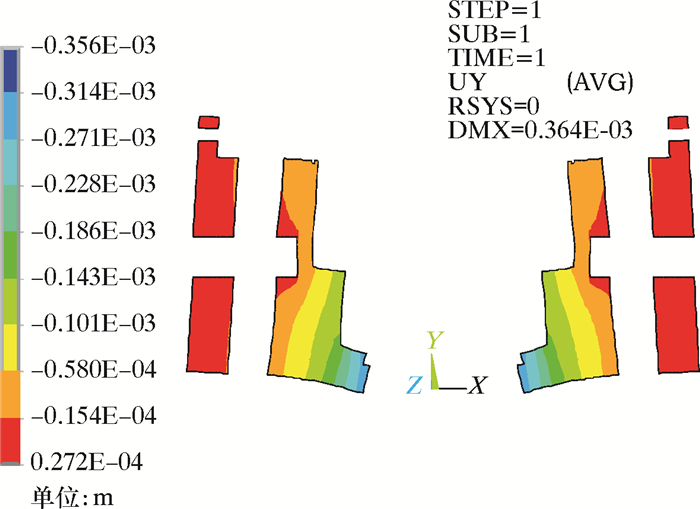
|
| 图 9 下齿轮箱体法向变形XY剖面 Fig.9 XY cross section of the normal deformation of the lower gear box |
从图 8、图 9及表 2可知,在垂直载荷作用下,法向变形为主要变形,最大变形位置为箱体与承载法兰接触面;箱体上半部分孔径在X向为径向收缩变形,在Z向为径向拉伸变形;而在箱体下半部分孔径在X向为径向拉伸变形,在Z向为径向收缩变形;A、B、C平面的法向位移绝对值的最大值为0.264 mm,最大平面变形挠度为0.147 mm,D、E柱面的最大收缩变形为0.201 mm,最大扩张变形为0.163 mm,满足结构刚度的安全设计要求。
| 平面 | A | B | C | 柱面初始曲率半径 | ||||||||
| 法向位移 | 变形挠度 | 法向位移 | 变形挠度 | 法向位移 | 变形挠度 | D | E | |||||
| 变形值 | -2.64×10-4 | 7.01×10-5 | -1.48×10-4 | 1.24×10-4 | -1.23×10-4 | 1.47×10-4 | 2.58×10-1 | 3.40×10-1 | ||||
| 柱面 | 顶面中心点 | 底面中心点 | 最大收缩变形 | 最大扩张变形 | ||||||||
| 径向位移 | X向位移 | Z向位移 | 径向位移 | X向位移 | Z向位移 | |||||||
| D | 5.57×10-5 | -2.31×10-5 | -5.07×10-5 | 7.91×10-5 | 4.74×10-5 | -6.33×10-5 | -1.27×10-4 | 9.47×10-5 | ||||
| E | 1.30×10-4 | -1.01×10-4 | 8.15×10-5 | 4.97×10-5 | -2.02×10-5 | -4.54×10-5 | -2.01×10-4 | 1.63×10-4 | ||||
3 下齿轮箱体的结构优化及结果分析
侧壁壁厚t和底部壁厚h是2个显著影响下齿轮箱体刚度的设计参数。其中侧壁壁厚t与箱体的径向抗弯能力密切相关,而底部壁厚h对箱体的法向抗弯能力有重要影响[8],因此,在优化计算中,将侧壁壁厚t和底部壁厚h作为设计变量。
侧壁壁厚t的初始设计尺寸为75 mm,在优化计算中,t的设定范围为[50,100],选取如下5个参数值:50.0、62.5、75.0、87.5、100.0;箱体底部壁厚h的初始设计尺寸为100 mm,h的设定范围为[75,125],选取如下5个参数值:75.0、87.5、100.0、112.5、125.0。由求解器计算得到的结果见图 10、图 11和图 12。
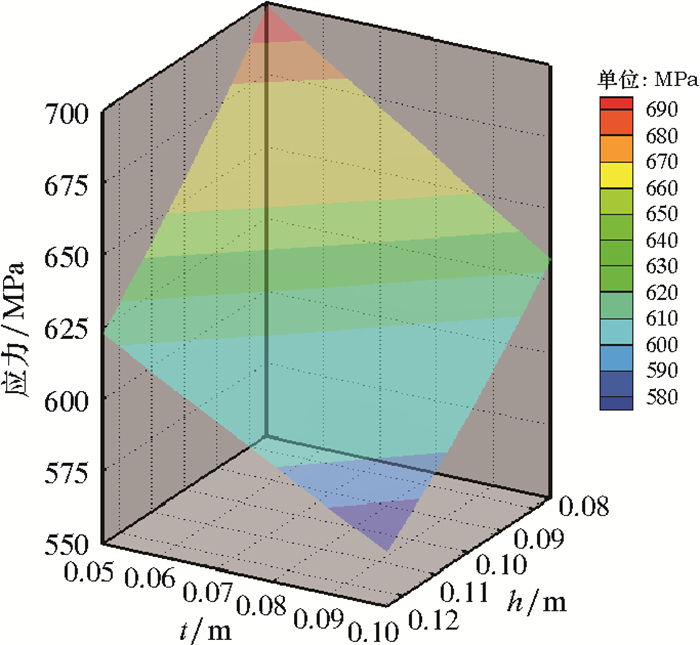
|
| 图 10 下齿轮箱体侧壁壁厚及底部壁厚与箱体销轴处最大应力关系 Fig.10 The relation between the side and bottom wall thickness and the maximum stress at the hinge pin of the lower gear box |
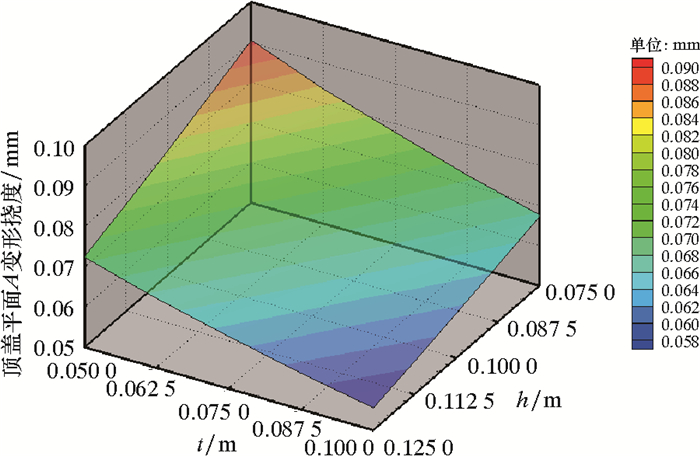
|
| 图 11 下齿轮箱体侧壁壁厚及底部壁厚与顶盖平面A变形挠度关系 Fig.11 The relation between the side and bottom wall thickness and the deformation deflection of the top cover plane A of the lower gear box |
|
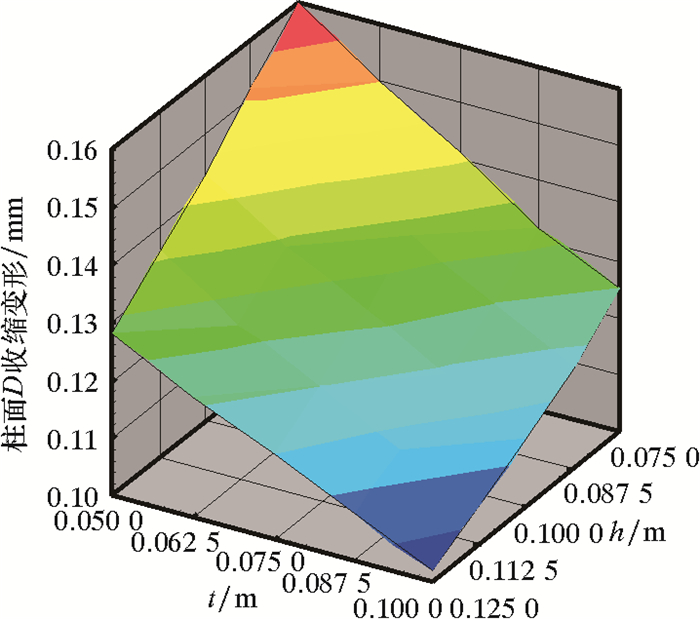
| 图 12 下齿轮箱体侧壁壁厚及底部壁厚与箱体柱面D收缩变形关系 Fig.12 The relation between the side and bottom wall thickness and the shrinkage deformation of the cylinder surface D of the box of the lower gear box |
(1) 侧壁壁厚与底部壁厚越大,销轴处最大应力越小,侧壁壁厚与底部壁厚对销轴最大应力的影响水平相当;
(2) 侧壁壁厚与底部壁厚越大,平面A变形挠度越小,但侧壁壁厚对平面A变形挠度的影响更大;
(3) 侧壁壁厚与底部壁厚越大,柱面D收缩变形越小,侧壁壁厚与底部壁厚对柱面D收缩变形的影响水平相当。
通过下齿轮箱体侧壁壁厚、底部壁厚与结构应力以及结构刚度的一系列关系图,可以获得优化变量与状态变量之间的对应关系,为箱体的最优设计提供详尽完备的数值依据。
4 结论(1) 下齿轮箱体提环销轴处最大应力为628 MPa,选用35CrMo材料可以满足结构强度安全设计要求。
(2) 在垂直载荷作用下,法向变形为主要变形,最大变形位置为箱体与承载法兰接触面,从各个刚度参数来看,满足下齿轮箱体结构刚度的安全设计要求。
(3) 侧壁壁厚与底部壁厚对下齿轮箱体结构强度和刚度均有影响,通过优化变量与状态变量之间的对应关系可以获得下齿轮箱体的最优结构参数。
(4) 通过ANSYS的全参数化设计计算过程,很容易得到改变几何参数后结构的强度和刚度结果,大大提高了后续设计和改进工作的效率。
| [1] | 梁应红, 王中杰, 张亚强, 等. Tesco液压顶部驱动装置的优点及现场应用[J]. 石油矿场机械, 2005, 34(4): 81–83. |
| [2] | 贾柳. 典型顶部驱动钻井装置的结构与功能探究[J]. 设备运维, 2015(32): 22. |
| [3] | 李汉荣, 习玉光. 国外500 t顶驱装置技术性能分析[J]. 国外油田工程, 2004, 20(1): 37–39. |
| [4] | 周宁宁. 石油钻机顶部驱动钻井装置研究[J]. 中国石油和化工标准与质量, 2014(9): 61. |
| [5] | 程自力, 吴慧. 石油顶驱钻井装置悬挂体的静态有限元强度分析[J]. 中国科技信息, 2009(19): 36–37. DOI: 10.3969/j.issn.1001-8972.2009.19.012 |
| [6] | 张洪生, 邓桐, 曹立宏. 9000 m顶部驱动钻井装置结构选型研究[J]. 机械设计, 2015, 32(3): 100–104. |
| [7] | 刘鸿文. 材料力学Ⅰ[M]. 4版. 北京: 高等教育出版社, 2004. |
| [8] | 张学亮. 齿轮箱模态分析和结构优化方法研究[D]. 太原: 太原理工大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10112-2010143848.htm |



