0 引言
自动化钻井技术是21世纪钻井技术的重要发展方向[1],旋转导向钻井工具是其典型代表。与传统的滑动导向钻井相比,旋转导向钻井具有摩阻与扭矩小、井眼净化效果好、位移延伸能力强、井眼轨迹平滑易调控以及适用于高难度井和特殊油藏等特点[2-4]。
根据导向偏置机构的工作原理,旋转导向钻井工具可分为推靠式和指向式2种。根据导向工具的钻铤是否全旋转,旋转导向钻井工具又可分为动态式和静态式2种。由此现有旋转导向钻井工具共有4种组合方式,其中动态指向式旋转导向钻井工具是目前最先进的自动化钻井工具。安装在导向钻井工具内部的稳定平台为偏置机构提供一个对地静止的参考系,在该参考系下确定所要调节的工具面角,进而实现指向式旋转导向钻井功能。因此,稳定平台控制的性能指标将直接决定动态指向式旋转导向钻井工具的导向能力与导向精度。
由于技术保密的缘故,动态指向式旋转导向工具稳定平台的控制方法鲜有报道,能够查到的控制理论与方法文献集中在动态推靠式旋转导向钻井工具,且大多为仿真结果。二者的不同之处在于:动态推靠式旋转导向工具的稳定平台通过钻井液为钻头提供导向力,机械结构上不与钻头连接轴直接相连,扰动主要来自钻井液的水力波动和钻铤的随机转速波动,扰动的特点是频率高、幅度小;动态指向式旋转导向钻井工具的稳定平台与钻头连接轴直接相连,扰动主要来自钻头破岩过程中产生的高频力矩扰动和钻铤随机转速波动,扰动的特点是随机性强、幅度大。因此,需要专门研究动态指向式旋转导向钻井工具稳定平台的测控算法,以精确控制动态指向式旋转导向钻井工具成功命中地质目标。
1 动态指向式旋转导向钻井工具动态指向式旋转导向钻井工具原理样机的结构如图 1所示,主要由驱动连接轴、钻铤、稳定平台驱动电机、稳定平台、稳定平台电子仓、钻头连接轴、万向节、钻头、双偏心环机构及轴承等部分组成。在实验室条件下,通过驱动连接轴外接伺服电机带动钻铤转动,以模拟不同工况下的钻铤转动形式。

|
| 图 1 动态指向式旋转导向钻井工具结构图 Fig.1 Structural schematic of the dynamic point-the-bit rotary steerable drilling tool 1—驱动连接轴;2—钻铤;3—稳定平台驱动电机;4—稳定平台;5—稳定平台电子仓;6—轴承;7—双偏心环机构;8—钻头连接轴;9—万向节;10—钻头。 |
稳定平台电子仓内安装有数据处理器、MEMS速率陀螺仪和工具面角测量传感器。稳定平台通过轴承安装在钻铤内部,稳定平台驱动电机与钻铤连接在一起,带动稳定平台围绕钻铤轴线旋转。正常钻井过程中,稳定平台驱动电机保持与钻铤转动方向相反的同速率反向转动,实现稳定平台的对地静止。稳定平台的圆周角位置由工具面角传感器测量,其对地转速由MEMS速率陀螺仪测量。稳定平台与钻头连接轴之间通过双偏心环机构连接,钻头连接轴通过万向节与钻铤连接。万向节为钻头连接轴提供调节支点。此外,钻铤的钻压和扭矩通过万向节传递到钻头上。
2 稳定平台控制系统设计调节双偏心环结构的偏心度可保持钻头连接轴的轴线与钻铤的轴线之间呈现一个固定的结构弯角,保持稳定平台的角位置稳定可实现导向机构工具面角的稳定,进而实现导向钻井功能[5]。
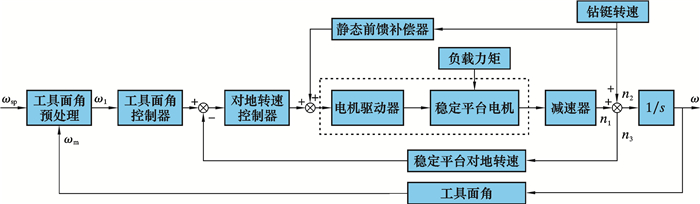
图 2为稳定平台控制系统框图。整个系统由2个反馈控制回路和1个静态前馈补偿通道组成。外环是工具面角位置控制回路。其中:ωsp为工具面角设定值,ωm为工具面角测量值,ω为工具面角输出值,ω1为经预处理后的工具面角测量值。内环是稳定平台对地转速控制回路,减弱稳定平台对地转速波动对工具面角控制精度的影响。其中:n1为稳定平台驱动电机通过减速器后的输出转速,n2为钻铤对地转速。在工具面角稳定的条件下,n1与n2大小相等,方向相反,二者叠加可得稳定平台对地转速n3,n3积分可得工具面角ω。n3由MEMS速率陀螺测量,ω由工具面角传感器测量。n2通过安装在钻铤上的陀螺仪测量,静态前馈补偿器对可测的钻铤转速进行扰动补偿。
|
| 图 2 稳定平台控制系统框图 Fig.2 Block diagram of stabilized platform control system |
工具面角控制器为主控制器,对地转速控制器为副控制器,二者均采用PI控制算法。静态前馈控制器根据稳定平台驱动器、驱动电机及减速器等环节的特性得到。负载力矩是指钻头连接轴传递到稳定平台上的负载力矩和稳定平台各种摩擦力矩。
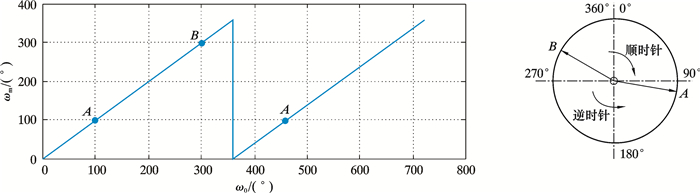
3 角位置测量值预处理方法工具面角测量值ωm定义为以稳定平台高边为起点0°,稳定平台顺时针转过的角度,ωm∈[0°, 360°]。记稳定平台从高边起,顺时针转动的角度总和为ω0,ωm与ω0之间变化关系如图 3所示。当稳定平台转动的角度是360°的整数倍时,工具面角测量值会出现从360°到0°的突变。如果对该突变不进行处理,将导致控制系统的偏差大小与偏差符号发生突变,进而使稳定平台驱动电机突然加速或者减速,破坏了系统的稳定性,甚至使控制系统无法正常工作。
|
| 图 3 稳定平台角位置测量值的变化 Fig.3 Variation of the measured value of the angle position of the stabilized platform |
设工具面角设定值ωsp=100°,如图 3中A点所示;当前工具面角传感器测量值ωm=300°,如图 3中B点所示。稳定平台顺时针转动160°或者逆时针转动200°,都可以从B点到达A点,显然顺时针转动是最优方案。因此,角位置控制中需要根据角位置设定值与测量值之间的相对位置来确定稳定平台的转动方向。文献[6]提出了一种通过偏差角变换和电机转向逻辑实现角度跳变的预处理方法,但是并没有提出一种可以用公式量化表示的处理方法,且实现较为复杂。
理论上,控制器的输入量为设定值与测量值的偏差,与设定值和实测值的具体数值无关。当ωsp=180°时,设定值位于0°~360°的中间,设定值与0°和360°测量值之间偏差绝对值相等,且在0°~180°或180°~360°的范围内连续变化,不会出现跳变。如果规定偏差为正时电机顺时针旋转,为负时逆时针旋转,就可以得到电机的转向控制方法。笔者提出了一种新的角位置测量值预处理方法,将不同设定值ωsp下的测量值ωm都映射为设定值在180°时的测量值,将控制器的设定值固定为180°,既解决了测量值突变对控制系统稳定性和参数整定的影响,也解决了电机的转动方向问题。偏差记为:
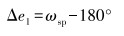
|
(1) |
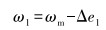
|
(2) |
式中:Δe1为当前设定值ωsp与180°之间的偏差。
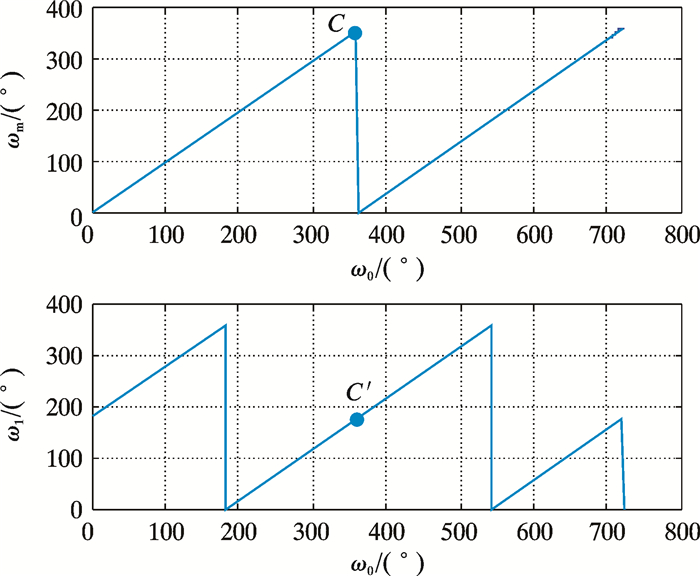
对于映射处理后ω1∉[0°, 360°]的情况,需要对ω1进行加减360°模量的处理,使ω1∈[0°, 360°]。一个极端的例子如图 4所示。令ωsp=360°,当稳定平台处于设定值C点附近时,ωm很容易出现负跳变,控制系统难以保持稳定。采用式(1) 和式(2) 处理后,C点将位于ω1=180°的C′点位置,此时参数整定与设定值为ωsp=180°时相同。
|
| 图 4 稳定平台角位置映射图 Fig.4 Angle position mapping of stabilized platform |
上述处理方法的本质是将控制器设定值固定为180°,通过关系解算将任意设定值ωsp下的测量值ωm都映射为控制器设定值为180°时的测量值ω1。该处理方法不但解决了稳定平台转向控制和角度跳变对控制器参数的影响,而且通过该方法可以只针对ωsp=180°时的情况进行参数整定和测试,大大降低了控制器参数整定的难度。该方法同样适用于类似的圆周角位置控制系统。
4 导向工具的性能测试 4.1 原理样机简介动态指向式旋转导向钻井工具原理样机如图 5所示。原理样机内部空间受限,实验室条件下钻铤内部的稳定平台驱动电机和稳定平台电子仓的测控元件,通过导电滑环与外部进行电气和信号连接,主控制板和稳定平台电机驱动器安装在钻铤外部,钻铤由外接伺服电机驱动。

|
| 图 5 原理样机 Fig.5 Prototype 1—外接伺服电机;2—导电滑环;3—钻铤;4—钻头;5—主控制板;6—稳定平台电机驱动器。 |
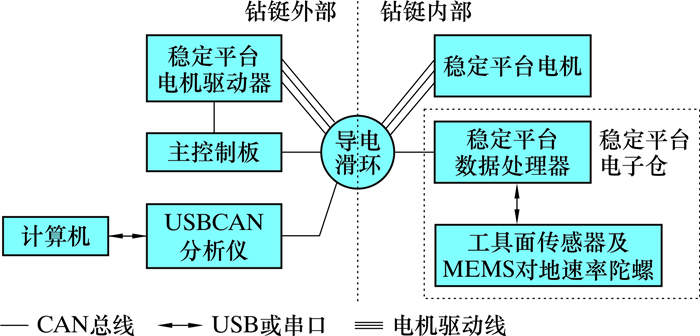
图 6为原理样机硬件连接图。稳定平台电子仓中的稳定平台数据处理器完成工具面角和稳定平台对地转速等信号的采集,并将数据重新编码后经由CAN总线发送到位于钻铤外部的主控制板。图 2中的工具面角控制器和对地转速控制器均由主控制板实现。主控制板计算的稳定平台电机转速通过CAN总线将转速设定值发送给稳定平台电机驱动器,电机驱动线经导电滑环连接到稳定平台电机,实现稳定平台的闭环控制。此外,CAN总线上连接USBCAN分析仪,通过计算机对CAN总线上的数据进行采集分析。
|
| 图 6 原理样机硬件连接图 Fig.6 Hardware connection diagram of the prototype |
4.2 建模与仿真
笔者首先分析稳定平台电机转速设定值与稳定平台电机实际转速值之间的传递函数模型结构与阶次;然后通过实际测试数据,辨识得到传递函数模型各未知参数具体数值;最后利用Simulink软件进行稳定平台控制系统仿真试验。忽略逆变桥、转速传感器、三相电枢电流传感器和电机反电动势对稳定平台电机控制回路的影响,伺服电机速度环控制框图如图 7所示[7]。其中,各传递函数为:
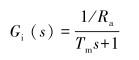
|
(3) |
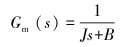
|
(4) |

|
| 图 7 伺服电机速度控制框图 Fig.7 Speed control diagram of servo motor |
式中:Ra为电枢电阻,Tm为电机电气时间常数,J为电机与负载的转动惯量,B为黏滞摩擦因数。
PI控制器的传递函数为:
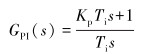
|
(5) |
式中:Kp和Ti分别为控制器的比例系数和积分时间。
根据图 7可以确定稳定平台转速环传递函数Gc(s)的基本结构如下:

|
(6) |
式中:A21、A11、A01、A42、A32、A22、A12及A02均为待辨识参数。
稳定平台电机额定转速为2 280 r/min,从100~2 280 r/min范围内每隔100 r/min测量1组电机转速曲线,利用获取的23组数据辨识可得稳定平台转速传递函数Gc(s)为:
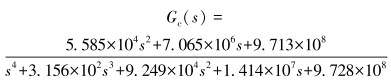
|
(7) |
式(7) 对所有样本数据的拟合度都保持在60%以上。图 2中的减速器减速比为8,伺服电机速度控制可实现无静差跟踪。因此,设计静态前馈控制器的传递函数GPD(s)为:
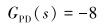
|
(8) |
利用式(7) 和式(8) 的传递函数和图 2的控制系统框图可构建原理样机的仿真系统。
控制器参数整定工作针对稳定平台对地转速环和稳定平台工具面角控制环,按照先整定内环再整定外环的原则,利用Simulink自带参数优化工具箱,设计主副控制器参数,为原理样机参数整定提供参考。
4.3 原理样机的参数整定在主控制板上编写增量式PID工具面角控制器和增量式PID工具面角控制器,对地转速环控制周期为10 ms,工具面角控制环控制周期为20 ms。稳定平台对地转速环参数整定时要求调节时间尽可能短,强调系统的稳定性与快速性。结合原理样机测试参数和钻井技术需求[8],确定内环调节时间小于0.6 s,利用仿真平台获取一组理想情况下的PID参数,然后在原理样机上进行测试。
稳定平台工具面角控制回路参数整定时希望稳态误差小,强调控制系统的准确性。依据文献[8]提出的钻井技术要求,确定主控制器回路性能指标为:超调量小于50%,调节时间短于7 s,工具面角ω稳态误差小于1°。
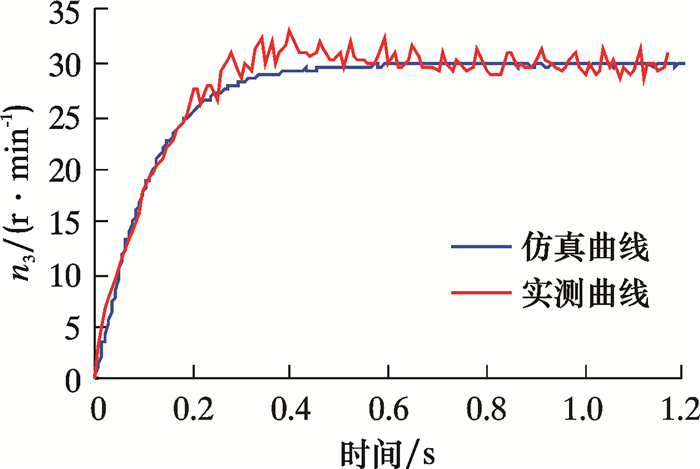
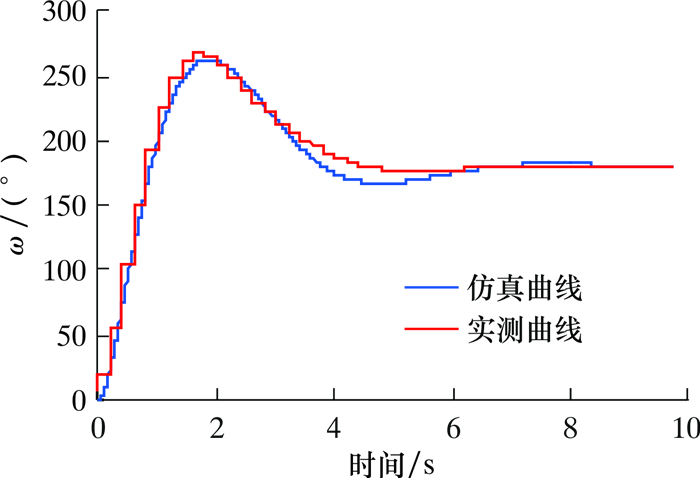
仿真和实测选用的PID参数如表 1所示。实际测试过程中,需要对仿真优化的控制器参数进行微调,使仿真结果与实测结果一致。稳定平台的转速环响应曲线见图 8。实测数据有6%的超调,调节时间短于0.5 s。角位置环采用的工具面角传感器数据更新间隔为200 ms,实测与仿真曲线如图 9所示。系统超调为48%,调节时间为6.5 s,稳态误差为0.5°,达到了设计的性能指标。表 1中仿真和实测的PID参数相差在2倍以内,且图 8和图 9的仿真曲线与实测曲线的整体趋势和调节时间基本相同,间接证明了模型阶次及其参数的准确性。
| 项目 | 对地转速环参数 | 角位置环参数 | |||
| Kp | Ti | Kp | Ti | ||
| 仿真 | 0.350 0 | 0.005 0 | 0.200 0 | 1.250 0 | |
| 实测 | 0.195 6 | 0.005 0 | 0.200 0 | 2.500 0 | |
|
| 图 8 稳定平台对地转速环的响应曲线 Fig.8 The speed loop response of stabilized platform |
|
| 图 9 稳定平台角位置环的响应曲线 Fig.9 The angle position loop response of stabilized platform |
4.4 原理样机抗扰动性能测试
井下黏滑现象是一种对稳定平台控制性能影响较大的干扰因素,在旋转导向控制系统设计中需要重点考虑。国内外研究机构大多通过对控制系统进行阶跃干扰和斜坡干扰测试,间接反映控制系统对井下干扰的抑制能力,尚未发现导向钻井系统抗黏滑扰动的相关文献以及有关黏滑过程的模拟测试。
当黏滑现象发生时,钻头处实际转速会发生大幅波动,且该波动在平均转速附近符合正弦变化规律,变化频率在0.05~0.50 Hz之间[9-11]。常见的黏滑程度S%表示方法如下[12]:
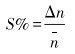
|
(9) |
式中:Δn表示最大转速波动值与平均转速的差值,n为钻头处的平均转速。
选择黏滑度为100%,平均转速96 r/min,变化频率为0.5 Hz的黏滑扰动进行测试,钻铤转速可以简化为:
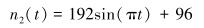
|
(10) |
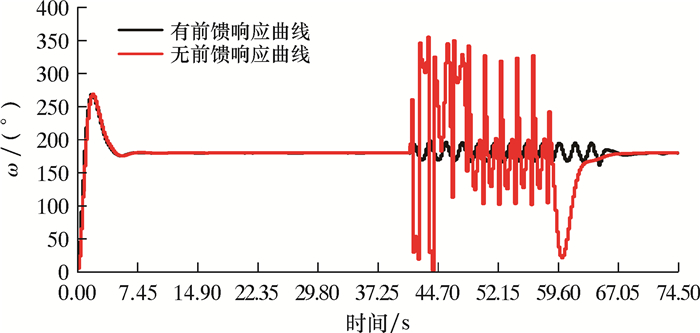
分别对稳定平台工具面角反馈-前馈控制系统和无前馈稳定平台工具面角控制系统进行井下黏滑扰动的模拟测试。先将工具面角由0°调整到180°,当工具面角稳定在180°以后,再加入式(10) 所示的钻铤黏滑扰动,测试2种控制系统在黏滑工况下的性能变化,结果如图 10所示。
|
| 图 10 黏滑扰动的响应曲线 Fig.10 Response of stick-slip |
由图 10可知,2种控制系统在工具面由0°调整到180°的过程中响应曲线基本一致。在黏滑工况扰动下,无前馈控制系统的工具面角出现大幅波动,稳定后工具面角的波动范围为103°~341°,波动幅度为-77°~161°。反馈-前馈控制系统的工具面角在设定值180°附近出现类似正弦的波动变化,波动幅值为±13°,波动频率与钻铤扰动频率相同。
由此可见,反馈-前馈控制系统可以较好地抑制黏滑工况造成的工具面角波动,在黏滑度100%的情况下仍然能够将工具面角控制在±13°范围内。实际钻井工程中,工具面角在±20°之间波动仍然可以成功命中地质目标,上述控制精度满足实际钻井过程中的技术要求。
5 结论(1) 针对稳定平台圆周角位置控制中存在的测量值周期性突变现象,提出了一种角位置预处理方法,解决了电机转向控制和测量值跳变问题,简化了控制系统设计,降低了控制器参数整定难度。
(2) 结合理论建模与系统辨识方法,获取了旋转导向原理样机稳定平台的控制模型,进而搭建了稳定平台工具面角反馈-前馈仿真系统,为原理样机的参数整定和控制算法研究提供了依据。通过仿真得到的控制器参数微调后即可应用在原理样机上,且原理样机响应曲线与仿真曲线基本一致。
(3) 针对井下黏滑工况进行了测试,反馈-前馈控制系统可以较好地抑制黏滑工况造成的工具面角波动,在黏滑度100%的情况下可将工具面角控制在±13°范围内,满足钻井过程中的技术要求。
| [1] | 沈忠厚, 黄洪春, 高德利. 世界钻井技术新进展及发展趋势分析[J]. 中国石油大学学报(自然科学版), 2009, 33(4): 64–70. |
| [2] | 薛启龙, 丁青山, 黄蕾蕾. 旋转导向钻井技术最新进展及发展趋势[J]. 石油机械, 2013, 41(7): 1–6. |
| [3] | 刘新华, 董广华, 赵洪山, 等. 旋转导向井下工具控制系统设计及室内试验[J]. 石油钻探技术, 2011, 39(5): 86–90. |
| [4] | 薛启龙, 韩来聚, 杨锦舟, 等. 旋转导向钻井稳定平台控制系统仿真研究[J]. 石油钻探技术, 2010, 38(4): 10–14. |
| [5] | 耿艳峰, 王伟亮, 鄢志丹. 动态指向式旋转导向钻井工具及其测控方法: 104832088[P]. 2015-08-12. |
| [6] | 汤楠, 汪跃龙, 霍爱清, 等. 旋转体圆周角位置控制方法[J]. 信息与控制, 2009, 38(4): 496–500. |
| [7] | 寇宝泉, 程树康. 交流伺服电机及其控制[M]. 北京: 机械工业出版社, 2008: 68-71. |
| [8] | 汪跃龙, 王海皎, 康思民, 等. 导向钻井稳定控制平台的反馈线性化控制[J]. 石油学报, 2014, 35(5): 952–957. DOI: 10.7623/syxb201405016 |
| [9] | KYLLINGSTAD K, NESSJøEN P J. A new stick-slip prevention system[C]//SPE/IADC Drilling Conference and Exhibition. Society of Petroleum Engineers, 2009. |
| [10] | 章莉敏, 李江红, 姜庆巍. 基于自抗扰算法的钻杆黏滑控制方法研究[J]. 测控技术, 2014, 33(12): 92–94, 98. DOI: 10.3969/j.issn.1000-8829.2014.12.025 |
| [11] | WU X, PAEZ L C, PARTIN U T, et al. Decoupling stick/slip and whirl to achieve breakthrough in drilling performance[C]//IADC/SPE Drilling Conference and Exhibition. Society of Petroleum Engineers, 2010. |
| [12] | SUGIURA J. The use of the near-bit vibration sensor while drilling lead to optimized rotary-steerable drilling in push-and point-the-bit configurations[C]//SPE Asia Pacific Oil and Gas Conference and Exhibition. Society of Petroleum Engineers, 2008. |



