2. 中海油安全技术服务有限公司;
3. 中国石油大学(华东)储运与建筑工程学院
2. CNOOC Security & Technology Services Co., Ltd;
3. College of Pipeline and Civil Engineering, China University of Petroleum(Huadong)
0 引言
充气辅助携岩技术是一种特殊的钻井技术,通过气体举升,减小钻井泵循环压力,提高钻井液井底返速,从而达到辅助携岩目的[1-4]。按照注气方式的不同,充气辅助携岩技术分为地面立管注入法和地下充气法。地下充气法有多种形式,包括寄生管注入法、同心管注入法和连续管注入法等。充气欠平衡钻井在国内外的钻井施工中得到了广泛应用,众多研究者也对该技术做了很多研究。该技术中由于气体的可压缩性较液体大,在井壁垮塌或钻井液中岩屑体积分数变化大时,充气压力常难以控制,同时也会带来井底压力波动,而井底压力波动会加剧井壁失稳[3-4]。
针对充气辅助携岩技术的这一缺陷,国内油气田在煤层气钻井中尝试利用液体替换气体,利用液体可压缩性远小于气体及射流可产生负压的特点,形成了双管双循环携岩技术。该针对性改进技术已成功应用,并取得了良好的效果,但相关的研究较少。笔者利用CFDDEM耦合模型对双循环钻井技术进行再现,展示辅助循环的作用机理,并对辅助循环喷嘴进行计算和优化,以期进一步提高双循环钻井技术在煤层气中的钻井效率。
1 颗粒运动方程及Hertz-Mindlin接触模型固体颗粒在空间坐标系中的运动主要由平动和转动2种方式构成,颗粒总的运动方式则可以看作两者的叠加。颗粒运动方程为[5-6]:
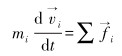
|
(1) |
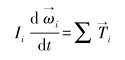
|
(2) |
式中:mi、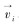
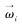
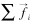
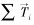
当颗粒j与颗粒i发生碰撞时,作用在颗粒i上的扭矩可由下式计算:
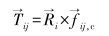
|
(3) |
式中: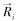
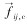
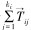
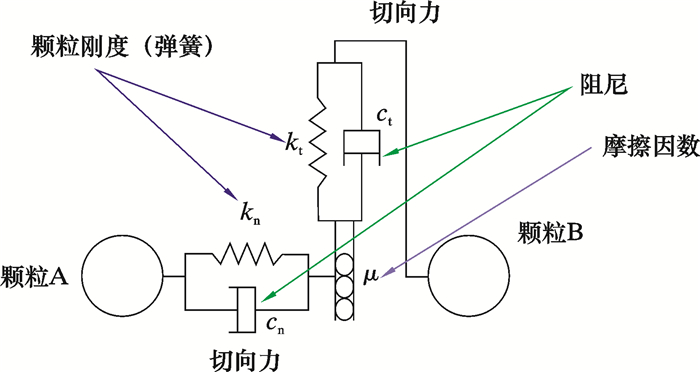
根据岩屑颗粒的物理性质及在钻井液中的表现,采用HertzMindlin无滑动颗粒接触模型并考虑颗粒间的滚动摩擦力。该模型是Mindlin在Hertz模型的基础上发展而来,模型如图 1所示。假设2个弹性球体接触时,2球间通过摩擦力达到平衡,2个球之间不发生相对滑移[7]。
|
| 图 1 Hertz-Mindlin颗粒接触模型简化图 Fig.1 Schematic diagram of the Hertz-Mindlin particle contact model |
颗粒法向接触力为:
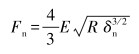
|
(4) |
式中:E为固体颗粒弹性模量,R为等效半径,δn为法向位移量。
法向阻尼力为:
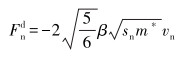
|
(5) |
式中:m*为等效质量,vn为相对速度的法向分量,sn和β为法向刚度分量,由恢复系数决定。
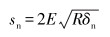
|
(6) |
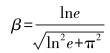
|
(7) |
式中:e为弹性恢复系数
切向力基于法向位移量建立,其表达式为:
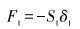
|
(8) |
式中:δt为切向位移向量,St为切向刚度,即在单位切向力作用下球心发生的切向位移量,可由下式计算。
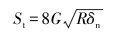
|
(9) |
式中:G为等效剪切模量。
2球状颗粒的切向阻尼为:
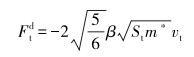
|
(10) |
式中:vt为相对切向速度。
切向力受库伦摩擦力的限制,即有:
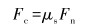
|
(11) |
式中:μs为静摩擦因数。
滚动摩擦力是通过在接触表面施加力矩来考虑的,即:
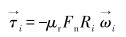
|
(12) |
式中:μr为滚动摩擦因数。
流体与固体颗粒间质量、动量和能量等的传递来实现二者的耦合,流体的相关理论此处不再赘述[8-9]。在计算中,流体相湍流模型采用标准κ-ε湍流模型描述。颗粒与壁面的碰撞视为颗粒间碰撞,将壁面看作一个半径无穷大且质量无穷大、速度为0的颗粒来处理。
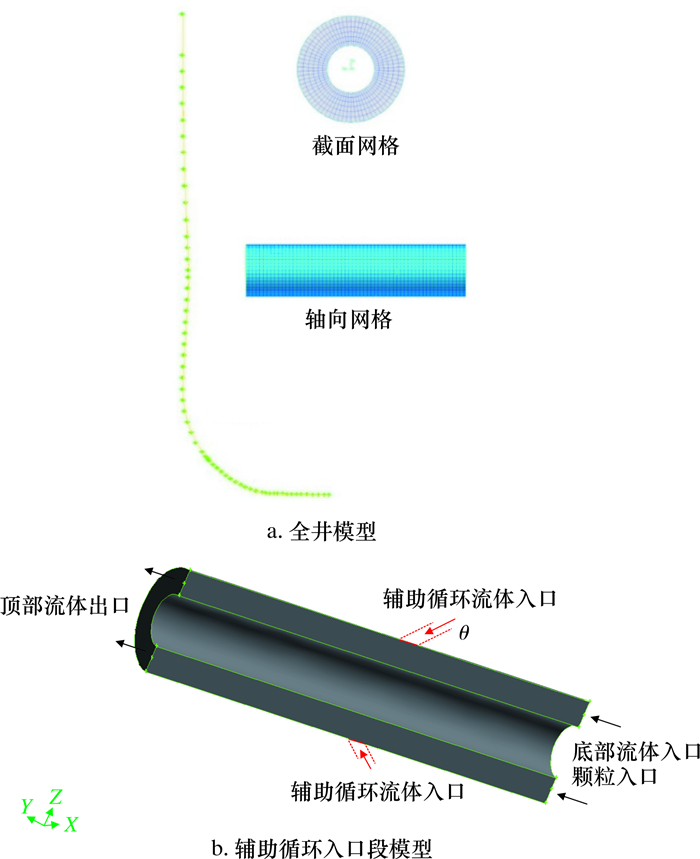
2 双循环系统仿真模型 2.1 CFD-DEM模型建立根据实钻煤层气井ZS-3井的井眼轨迹资料、井筒参数及钻井操作参数等进行实井建模,分析辅助循环系统的加入对全井携岩效果的改善作用。全井CFD模型及岩屑颗粒DEM模型如图 2所示,模型参数见表 1。其中,辅助循环喷嘴在同一井周截面均匀布置2个,入射角度为流体入射方向与井眼轴线夹角;岩屑入口体积分数根据ZS-3井正常钻速(50 m/h)推算。计算域中网格最小尺寸为0005 m,最大网格尺寸为0050 m,最小单元格体积为37×10-8 m3,最大单元格体积为13×10-5 m3,总网格数量为2 490 606。
|
| 图 2 双循环全井仿真模型及入口段模型 Fig.2 Whole well simulation model of double-circulation system and inlet section model |
| 参数 | 数值 |
| 井深/m | 1 000 |
| 主循环流量/(L·s-1) | 15 |
| 辅助循环流量/(L·s-1) | 14 |
| 外层套管直径/mm | 177.8 |
| 内层套管直径/mm | 130.0 |
| 钻柱直径/mm | 88.9 |
| 钻杆旋转速度/(rad·s-1) | 7.33 |
| 钻井液密度/(g·cm-3) | 1.06 |
| 钻井液黏度/s | 45 |
| 喷嘴井深位置/m | 780 |
| 喷嘴直径/mm | 10 |
| 入射角度/(°) | 30 |
| 岩屑入口体积分数/% | 0.2 |
| 岩屑颗粒粒径/mm | 2 |
| 颗粒密度/(g·cm-3) | 2.26 |
| 泊松比 | 0.23 |
| 剪切模量/GPa | 11.8 |
| 滚动摩擦因数 | 0.01 |
2.2 结果分析
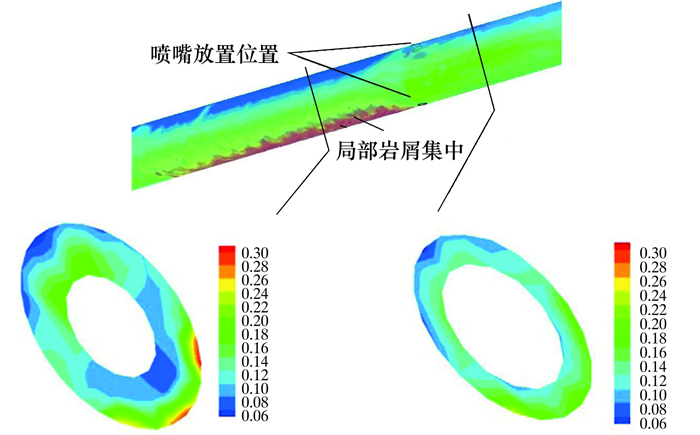
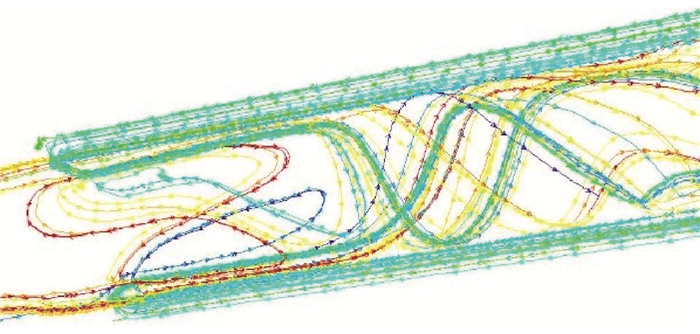
图 3显示了喷嘴周围的岩屑体积分数分布。通过井眼环空截面结果可以看出,在辅助循环喷嘴的下方存在明显的岩屑集中,而得益于辅助循环的加入,喷嘴上方截然不同,不存在岩屑颗粒的集中现象。图 4为喷嘴附近的钻井液流线图。图中显示了主循环及辅助循环钻井液在喷嘴处汇合并围绕模型内壁(即钻杆)旋转前进,但在喷嘴出口处由于辅助循环的高压力,流体由喷嘴内狭小空间射入井眼环空较大空间时压力突降,导致局部负压及局部回流现象。
|
| 图 3 喷嘴周围岩屑体积分数分布云图 Fig.3 Distribution of the volume fraction of cuttings around the nozzle |
|
| 图 4 喷嘴周围流体运动轨迹线 Fig.4 Fluid trajectory around the nozzle |
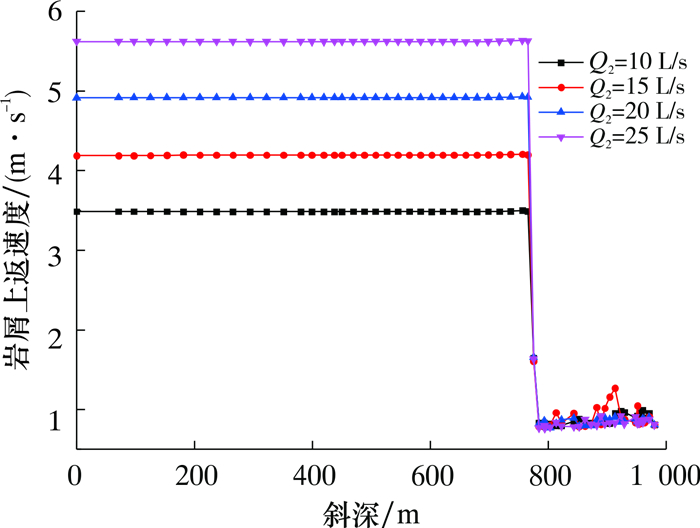
提取不同井深处井眼环空岩屑运移速度平均值,得到不同辅助循环流量Q2下环空岩屑上返速度随斜深变化曲线,如图 5所示。由图可知,在其他参数一定时,辅助循环流量的增加使岩屑的上返速度提升明显;另外,在辅助循环喷嘴以下的井眼区段,相比于喷嘴以上井段,仅有主循环作用时颗粒运移速度分布不够均匀,说明随着辅助循环的出现,大大改善了喷嘴以上井筒内的岩屑排出效果,该现象可在图 6中得到证实。
|
| 图 5 不同辅助循环流量下环空岩屑上返速度随斜深变化曲线 Fig.5 Effect of measured depth on the return velocity of the cuttings in annulus under different assistant circulation flow rate |
|
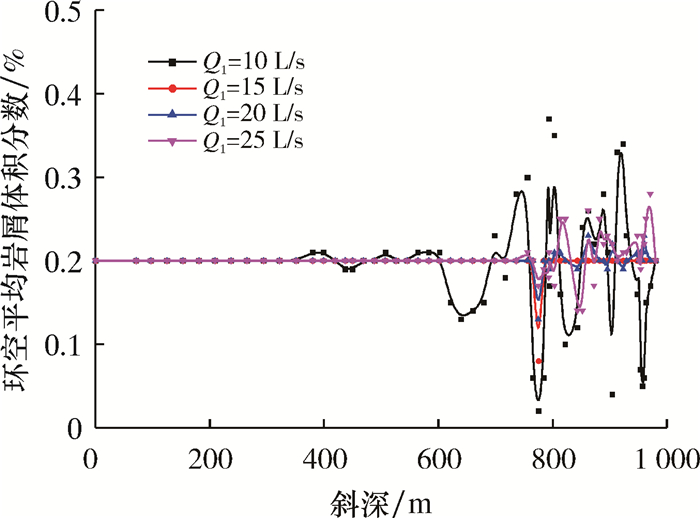
| 图 6 不同主循环流量下环空平均体积分数随斜深变化曲线 Fig.6 Effect of measured depth on the average cutting volume fraction in the annulus under different main circulation flow rate |
图 6是不同主循环流量Q1下井眼环空平均体积分数随斜深变化曲线。由图不难看出,主循环流量Q1增加时,喷嘴周围岩屑平均体积分数变小,显示了主循环流量对岩屑排出的正作用;同时,在水平段和弯曲段(600 m以上井段)岩屑的体积分数分布不均匀,而垂直段分布趋于平稳,表明井眼水平段和弯曲段岩屑运移的不均匀性,在井眼局部易出现集中。
由以上分析可知,双循环系统的共同作用对携岩效果的改善非常明显;而辅助循环喷嘴的设置起到关键作用,对喷嘴结构进行优化极其必要,特别是喷嘴角度。下面将通过截取喷嘴附近的局部模型,细化网格,降低计算消耗,对辅助循环入射角度进行优化。
3 辅助循环喷嘴入射角度优化出于结构的对称性,建立二维环空喷嘴计算模型。设定喷嘴直径20 mm,喷嘴入射角度θ在0°~75°之间变化,模型井眼环空长2 200 mm,环空间距44.5 mm,底部环空入口岩屑体积分数0.2%,岩屑粒径2 mm,钻井液的主循环及辅助循环入口流量均是15 L/s,模型边界条件设置与图 2b一致。
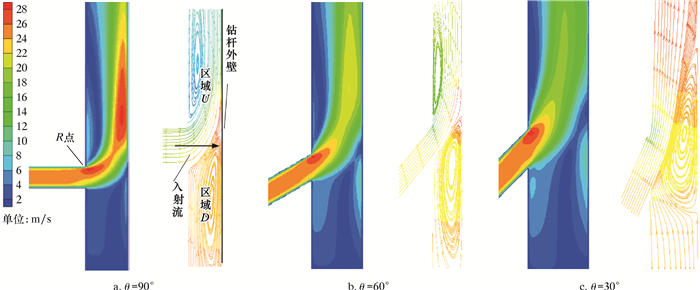
图 7为不同入射角度下喷嘴局部液体速度及流线分布图。由图 7可知,辅助循环钻井液以不同角度入射主井眼环空,与主循环钻井液汇合时,最大流速出现在接口上部(图中R点);主循环钻井液与辅助循环钻井液在相汇处形成局部回流,当入射角度较大时,入射口的上部及下部均出现回流(入射角为90°和60°流线分布图区域U和R),这是由于入射流冲击钻杆壁导致的;而入射角度较小时,上部回流消失,仅在下部出现局部回流(图中入射角度为30°时区域D所在位置)。
|
| 图 7 不同入射角度下喷嘴局部液体速度及流线分布 Fig.7 Local velocity and streamline distribution of nozzle at different shooting angles |
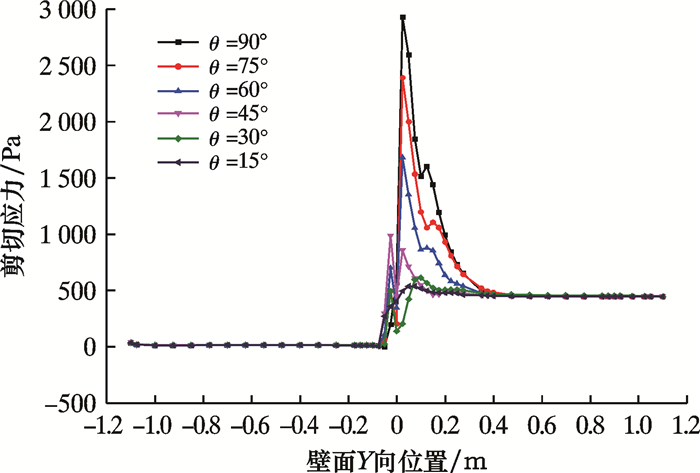
辅助循环喷嘴射出的较高流速钻井液会对钻杆形成直接冲击。图 8为不同入射角度下钻杆截面上的剪切应力分布曲线。由图可知,随着喷嘴倾角的增大,钻杆受冲击的剪切应力增大,在入射角度为90°时,由于喷嘴射流方向与井眼轴线垂直,且喷距较小,此时钻井液出射动量最大,对钻杆井壁的冲蚀作用最强,而该作用随入射角度的减小而减弱。
|
| 图 8 不同入射角度下钻杆截面上的剪切应力分布 Fig.8 Shear stress distribution on the drill pipe cross section under different shooting angles |
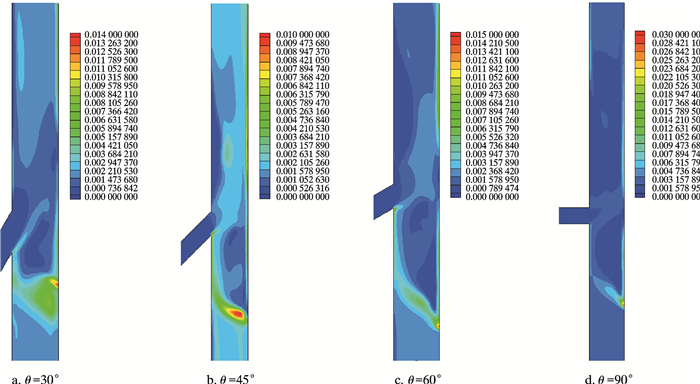
图 9为辅助循环喷嘴入射角不同时,喷嘴附近的岩屑颗粒体积分数分布云图。图中显示,岩屑最大体积分数出现在喷嘴下方钻井液回流区边缘;当入射角较大时(图 9c和图 9d),岩屑集中点紧邻钻杆壁(即计算区域右边界);当入射角过小时(图 9a),该集中点也出现在钻杆壁附近,而入射角为45°时(图 9b),该集中点向井眼环空中部移动。经过该岩屑集中点的垂直路径提取数据可以显示岩屑在喷嘴附近的分布状况,结果如图 10所示。
|
| 图 9 入射角不同时喷嘴附近颗粒相体积分数分布云图 Fig.9 Distribution of the volume fraction of the particles around nozzle under different shooting angles |
|
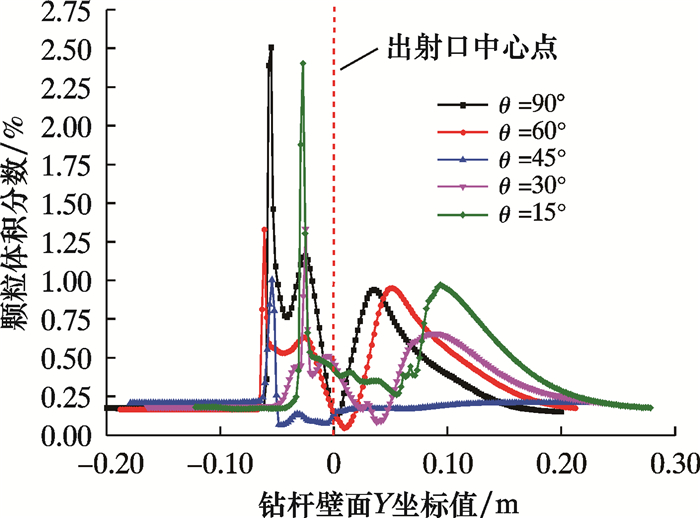
| 图 10 钻杆附近的岩屑颗粒体积分数垂直分布 Fig.10 Vertical distribution of cutting particles volume fraction near the drill pipe |
图 10显示了辅助循环喷嘴处的岩屑颗粒分布的不均匀性,喷嘴下部的局部回流造成局部岩屑集中(图中峰值),岩屑颗粒体积分数可达入口岩屑体积分数的5~12倍;在双循环交汇区以下(Y<-0.07 m)及以上区域(Y>0.25 m),岩屑分布趋于均匀。
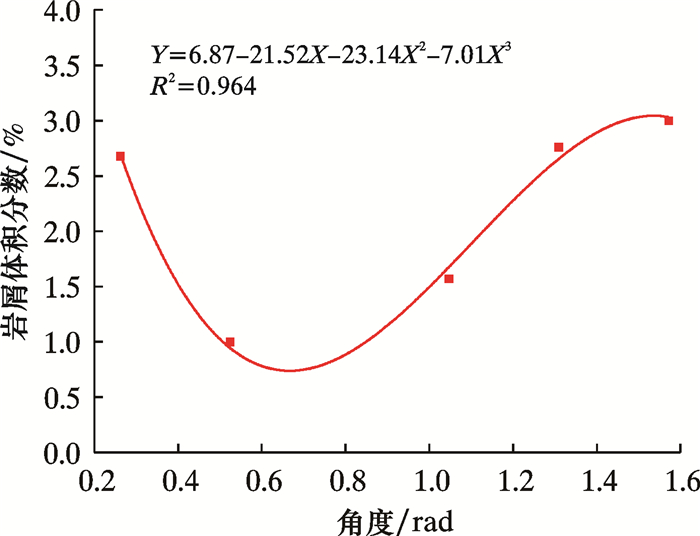
图 11为不同入射角度下钻井液-岩屑两相流场充分发展后井眼环空空间内岩屑的最大体积分数分布曲线。由图可见,随着喷嘴入射角度的增加,最大岩屑体积分数并不是单一的增加或减小,而是呈现先减小后增大的趋势,这主要是环空内局部回流变化导致的。可见,喷嘴入射角度在40°左右时岩屑体积分数最小,表明入射角度在40°±10°范围内时双循环系统携岩效果最好。
|
| 图 11 不同入射角度下最大岩屑体积分数曲线图 Fig.11 The maximum volume fraction of cuttings under different shooting angles |
4 结束语
笔者采用CFD-DEM耦合模型对煤层气钻井中采用的双循环钻井技术进行了数值再现,研究展示了辅助循环的作用机理,证实了辅助循环对改善钻井携岩效果的正作用;模拟结果揭示了喷嘴附近的流场分布,并对辅助循环喷嘴进行了计算和优化,分析结果表明:喷嘴入射角度在40°±10°范围时双循环系统携岩效果最好,辅助循环工作效果最佳。所得结论可为双循环钻井系统的现场应用提供参考。
| [1] | 刘大伟, 王益山, 虞海法, 等. 煤层气多分支水平井安全钻井技术[J]. 煤炭学报, 2011, 36(12): 2109–2114. |
| [2] | 乔磊, 申瑞臣, 黄洪春, 等. 煤层气多分支水平井钻井工艺研究[J]. 石油学报, 2007, 28(3): 112–115. DOI: 10.7623/syxb200703023 |
| [3] | 李根生, 刘文旭, 黄中伟, 等. 寄生管充气钻井环空多相流流动特性研究[J]. 石油机械, 2011, 39(3): 4–8. |
| [4] | 张义, 鲜保安, 赵庆波, 等. 煤层气欠平衡钻井环空注气工艺优化[J]. 石油勘探与开发, 2009, 36(3): 398–402. |
| [5] | FAVIER J. Industrial application of DEM:Opportunities and hallenges[M]. Edinburgh: DEM Solutions Ltd, 2008. |
| [6] | LU G, THIRD J R, MULLER C R. Discrete element models for non-spherical particle systems:From theoretical developments to applications[J]. Chemical Engineering Science, 2015, 127: 425–465. DOI: 10.1016/j.ces.2014.11.050 |
| [7] | RENZO A D, MAIO F P D. Comparison of contact force models for the simulation of collisions in DEM based granular flow codes[J]. Chemical Engineering Science, 2004, 59(3): 525–541. DOI: 10.1016/j.ces.2003.09.037 |
| [8] | 董长银, 高凯歌, 王鹏, 等. 低黏液体井筒携砂流动规律及特征流速实验[J]. 石油学报, 2016, 37(10): 1280–1286. DOI: 10.7623/syxb201610008 |
| [9] | 李皋, 胡强, 冯耀民, 等. 关于气体钻井全井段井筒冲蚀规律研究[J]. 计算机仿真, 2015, 32(10): 154–158. DOI: 10.3969/j.issn.1006-9348.2015.10.034 |



