0 引言
自由站立式立管系统是深水或超深水油气田开发的关键技术装备,它主要由基础底盘、刚性主管、浮力筒、柔性软管和浮式生产平台等组成[1-2]。其中,刚性主管是整个系统中跨度最大的结构单元。在刚性主管顶部,浮力筒提供巨大张力,以维持刚性主管的自由站立式形态。但是,不稳定的海洋环境载荷易导致浮力筒的周期性垂向运动,使刚性主管产生轴向振动。若浮力筒上、下运动的频率与刚性主管轴向振动的固有频率相等或接近,则系统会发生共振,产生极大的动载荷,从而危及到系统安全。为便于安装及操作,同时节约成本,浮力筒的位置应尽量靠近水面[3],此时波浪载荷对浮力筒的影响十分明显,垂向运动效应也更为突出,刚性主管受到的浮力筒惯性力也会急剧增大。
目前针对自由站立式立管系统的研究主要集中在刚性主管横向运动分析[2, 4-7]、局部连接结构强度分析[8]和基于受力状态的浮力筒结构设计[3, 9]等方面,尚缺乏浮力筒对刚性主管轴向振动的影响分析,而进行刚性主管轴向振动相关研究有助于完善浮力筒和刚性主管的力学性能分析,为自由站立式立管的系统设计提供有益参考,达到减缓轴向共振、确保作业安全的目的。
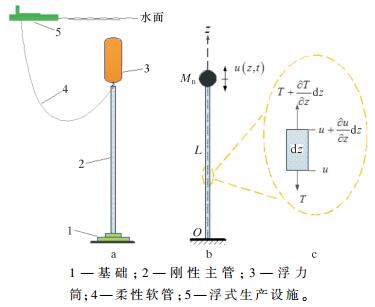
1 数值模型建立 1.1 力学模型典型的自由站立式立管系统如图 1a所示。其刚性主管在底部通过基础与井口相连,在顶部通过钢链与浮力筒相连,在顶部侧端通过柔性软管与浮式生产设施相连。
|
| 图 1 自由站立式立管系统及其力学模型示意图 Fig.1 The freestanding riser system and its mechanical model diagram |
为考察浮力筒对刚性主管纵向振动的影响,现以刚性主管和浮力筒为研究对象,不考虑柔性软管在连接处对刚性主管的垂向振动影响[9],建立如图 1b所示的轴向振动力学模型。其中,刚性主管底部被视为固定端,顶部被视为自由端;由于浮力筒惯性力的作用,模型顶端附带有集中质量单元。刚性主管顶部张力为浮力筒与刚性主管之间的内力。以基础固定端为原点O,以竖直向上为振动正方向(即z轴正方向),建立一维坐标系,则刚性主管微元体的受力状态如图 1c所示。受力平衡方程为:
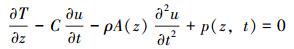
|
(1) |
式中:T为主管轴向张力,N; t为时间,s; C为线阻尼系数;A(z)为截面面积,m2;u(z)为轴向位移,m;ρ(z)为主管密度,kg/m3;p(z, t)为刚性主管单位长度上所受的轴向外力,N/m;图 1中MB为浮力筒等效质量,t;L为刚性主管长度,m。
在弹性范围内,轴向应变ε、位移及张力满足以下方程:
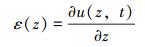
|
(2) |
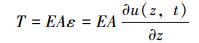
|
(3) |
将式(2) 和式(3) 代入式(1),得刚性主管的轴向振动方程为:
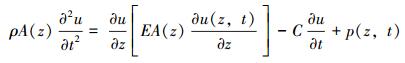
|
(4) |
式中:EA(z)为刚性主管的抗拉刚度, N。
假设主管的抗拉刚度和线质量为常量,且令C=0, p (x, t) =0,可得刚性主管的自由无阻尼振动微分控制方程为:
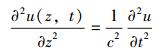
|
(5) |
式(5) 为波动方程,常量c≡E/ρ, 只与材料属性有关,表示振动波信号沿刚性主管轴向传播的速度。
采用分离变量法对式(5) 进行求解,假设振动函数为区域函数U(z)和时域函数φ(t)之积[10],即有:
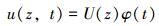
|
(6) |
式中:φ(t)=Accos(ωt)+Bcsin(ωt),Ac及Bc均为待定常量,可由初始条件确定,ω为刚性主管轴向的固有频率,rad/s。
由此可求得区域振型函数的解为:
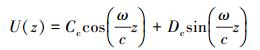
|
(7) |
式中:Cc及Dc均为待定常量,可由边值条件确定。
1.2 边界条件刚性主管的底端为固定端,其轴向位移边值条件为:
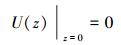
|
(8) |
刚性主管顶端的位移边值条件不确定,其力边值条件为:
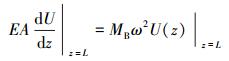
|
(9) |
综合式(7) 及式(8) 可知,消去振幅参量Dc可以确定分析系统的固有频率ω。
1.3 方程求解为方便计算,引入以下无量纲参数:
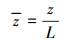
|
(10) |
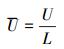
|
(11) |
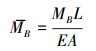
|
(12) |
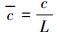
|
(13) |
将式(10)~式(13) 代入式(7)、式(8) 及式(9) 可得刚性主管在浮力筒和预应力作用下的频率控制方程为:
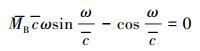
|
(14) |
由式(14) 可以看出,固有频率值ω为唯一变量,可通过数值方法进行求解,令:
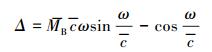
|
(15) |
当迭代频率ω以一定步长dω从0增加至一定值时,Δ发生相应变化。通过绘制Δ-ω曲线,可直观判断出固有频率的粗略值。在此基础上,可估计出固有频率值所在的区间。为精确求出固有频率,可采用局部求根法——割线法[11]对固有频率进行精确求解:
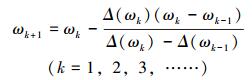
|
(16) |
初迭代频率值ω0及ω1分别为预估区间端点值。设置一定计算精度(采用误差e=1×10-4),通过若干循环,最终迭代收敛值即为所求的固有频率。
2 算例分析 2.1 计算参数西非海域某自由站立式立管的基本计算参数[3]:主管总长1 410 m,外径304.8 mm,厚度23.6 mm,立管密度ρ=7 850 kg/m3,弹性模量210 GPa,浮力筒等效质量192.7 t。
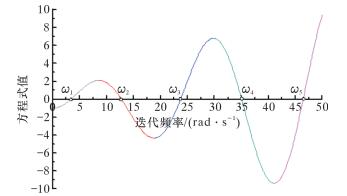
2.2 固有频率计算当迭代频率ω从0增加至一定值时,频率控制方程式值Δ的变化曲线如图 2所示。
|
| 图 2 方程式值Δ与迭代频率ω之间的关系 Fig.2 The relationship between the equation value Δ and the iteration frequency ω |
当Δ=0时,对应的横坐标即为所求固有频率的值。从图可看出,区间段[3, 4]、[12, 13]、[23, 24]、[34, 36]及[45, 47]即为刚性主管的第1阶、第2阶、第3阶、第4阶及第5阶固有频率区间;再利用局部求根割线法,求解出刚性主管的轴向振动固有频率为:ω1=3.363 2 rad/s,ω2=12.740 7 rad/s,ω3=23.719 1 rad/s,ω4=35.029 3 rad/s,ω5=46.441 8 rad/s。
2.3 浮力筒对刚性主管轴向振动的影响 2.3.1 浮力筒等效质量对固有频率的影响实际工程中,通过调节舱室的排水量来调节浮力筒的浮力,进而改变刚性主管的形态。但因长期服役,当浮力筒出现舱室破损时,海水会不断侵入浮力筒内。此时,浮力筒自身的等效质量发生变化。对于长度25 m,直径5.65 m的浮力筒,设其有20舱室和1个外径为1.74 m的中心管室,假设各舱室空间均匀,海水密度ρw=1 025 kg/m3。当海水侵入舱室数由0变化为20时,刚性主管的轴向固有频率也会随之发生变化。
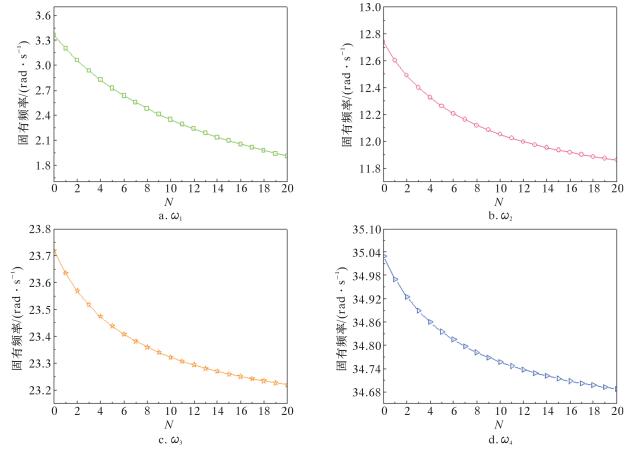
以海水入侵舱室数N为横坐标,以刚性主管轴向的固有频率为纵坐标,绘制两者的关系曲线,如图 3所示。
|
| 图 3 固有频率随海水入侵舱室数的变化曲线 Fig.3 The natural frequency with the seawater intrusion chamber numbers |
由图 3可知,当浮力筒破舱后,刚性主管固有频率降低;随着浮力筒破舱数的增加,刚性主管的轴向固有频率会越来越低。在相同破舱情况下,刚性主管的低阶频率比高阶频率下降量大,说明海水的侵入对刚性主管的低阶固有频率影响较大。
此外,结合以往研究实例[3],针对同样长径比的10舱室浮力筒(各舱室相同),当舱室完好在位、1舱破损、2舱破损、中心管(中心管外径为1.74 m)破损和中心管及1舱同时破损时,对应的顶部张力比、浮力筒等效质量MB和前4阶轴向固有频率ω1、ω2、ω3及ω4进行归纳,结果如表 1所示。
| 工况 | MB/t | ω1/(rad·s-1) | ω2/(rad·s-1) | ω3/(rad·s-1) | ω4/(rad·s-1) |
| ① 完好在位 | 192.70 | 3.363 2 | 12.740 7 | 23.719 1 | 35.029 3 |
| ② 1舱破损 | 250.85 | 3.058 8 | 12.490 9 | 23.569 2 | 34.925 1 |
| ③ 2舱破损 | 309.01 | 2.823 5 | 12.325 4 | 23.473 8 | 34.859 5 |
| ④ 中心管破损 | 253.63 | 3.046 2 | 12.481 5 | 23.563 7 | 34.921 3 |
| ⑤ 中心管及1舱同时破损 | 311.79 | 2.813 5 | 12.318 9 | 23.470 1 | 34.857 0 |
由表 1可看出,系统的前4阶固有频率受到浮力筒状态的显著影响,总体上与浮力筒的总等效质量成反相关,且在工况③ 和⑤ 下,频率最小。
2.3.2 浮力筒浮力对轴向振动的影响假设浮力筒受到的海水浮力为简谐力:
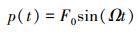
|
(17) |
式中:F0为最大等效张力,N;Ω为浮力筒垂向运动频率,rad/s。
根据底部的边界条件式(8) 所确定的自由无阻尼振型函数为:
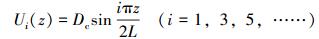
|
(18) |
由归一化条件[12]可知:
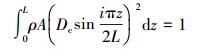
|
(19) |
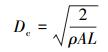
|
(20) |
正则广义力为:
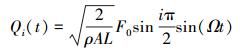
|
(21) |
正则坐标方程为:
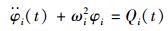
|
(22) |
由此可求得正则坐标下的稳态响应为:
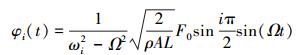
|
(23) |
由线性叠加原理[12]可得刚性主管在简谐张力作用下的稳态响应为:
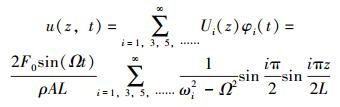
|
(24) |
可以直观地看出,刚性主管的稳态振幅与顶部浮力成正比,与立管密度、横截面面积及立管长度成反比。当浮力筒运动频率Ω与刚性主管轴向振动任意一阶频率ωi接近或相等时,稳态响应幅值在理论上都将趋于无穷大,此时视系统发生共振。
3 动载荷放大系数由式(24) 及式(9) 可知,在简谐浮力的作用下,刚性主管顶端受到的浮力筒最大稳态惯性力为:
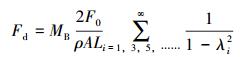
|
(25) |
式中:λi=ωi/Ω,为刚性主管各阶固有频率与浮力筒运动频率的比值,无因次。
对式(25) 取绝对值[12],做如下转换:
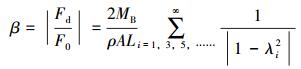
|
(26) |
可将F0视为顶部静张力,因此可将β视为刚性主管顶部的动载荷放大系数。对于表 1中的5种工况,根据式(26) 可分别计算出相应的动载荷放大系数。若浮力筒的垂向运动周期为3 s,即圆频率为2.094 4 rad/s,由于i=1,3,5,……,则取前1阶、前3阶和前5阶立管固有频率分别进行计算时,可获得5种工况下的动载荷放大系数,结果如表 2所示。
表 2中,动载荷放大系数明显偏大的工况也是工况③ 和工况⑤,这说明在2舱破损或中心管及1舱破损时,刚性主管所受的外力较大,其轴向应力较大,刚性主管可能被破坏。因此,在实际工作过程中,应加强浮力筒的健康状态监测,严禁出现2个以上舱室同时破损的情况。
| 工况 | 放大系数β | ||
| 前1阶 | 前3阶 | 前5阶 | |
| ① 完好在位 | 1.059 1 | 1.072 3 | 1.075 7 |
| ② 1舱破损 | 1.921 1 | 1.938 4 | 1.942 9 |
| ③ 2舱破损 | 3.280 0 | 3.301 5 | 3.307 0 |
| ④ 中心管破损 | 1.972 9 | 1.990 4 | 1.994 9 |
| ⑤ 中心管及1舱同时破损 | 3.362 4 | 3.384 1 | 3.389 6 |
4 结论及建议
(1) 利用数值迭代方法,并结合局部求根法——割线法,可快速而准确地求出自由站立式刚性主管轴向振动的固有频率。
(2) 当浮力筒舱室出现破损时,随着海水的侵入,刚性主管的固有频率会越来越低,且海水的侵入对低阶固有频率的影响较大。
(3) 刚性主管的稳态振幅与浮力筒浮力成正比,与刚性主管密度、刚性主管横截面面积和刚性主管总长度成反比。当浮力筒垂向运动频率与刚性主管的固有频率重合或接近时,刚性主管的稳态振幅在理论上为无穷大,此时视系统发生共振。
(4) 刚性主管顶部的动载荷放大系数与浮力筒的等效质量、刚性主管的密度、刚性主管的横截面面积、刚性主管的总长度及频率比(系统固有频率与激励频率比)有关。当浮力筒出现2舱破损、中心管及1舱同时破损的情况时,系统的动载荷放大系数明显偏大。
(5) 实际工作过程中,应考虑适当增加浮力筒设计水深,以减小垂向环境载荷作用,延长浮力筒垂向运动周期;通过合理设计及选材,尽量减小浮力筒的等效质量,以增大系统的固有频率;对浮力筒在役状态应加强维护及监测,避免出现破舱现象,尤其是出现2舱室以上的破舱现象。
| [1] | 张长智, 王桂林, 段梦兰, 等. 深水开发中的几种新型混合生产立管系统[J]. 石油矿场机械, 2010, 39(9): 20–25. |
| [2] | 康庄, 李辉, 孙丽萍, 等. 自由站立式立管总体运动疲劳分析[J]. 海洋工程, 2011, 29(4): 43–50. |
| [3] | 康庄, 贾鲁生, 孙丽萍, 等. 深水塔式立管顶部浮力筒设计分析方法[J]. 中国造船, 2011, 52(4): 118–129. |
| [4] | ZHOU X K, WANG D S, DUAN M L, et al. Numerical study on mode curvature for damage detection of a drilling riser using transfer matrix technique[J]. Applied Ocean Research, 2017, 63: 65–75. DOI: 10.1016/j.apor.2016.12.008 |
| [5] | SONG R X, STANTON P, ZHOU X L.Engineering design of deepwater free standing hybrid riser[C]//ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering.[S.l.]:Ocean, Offshore and Engineering Division, 2010:637-649. |
| [6] | KARUNAKARAN D N, LEE D, MAIR J.Qualification of the groped SLOR riser system[R].2009:1-15. |
| [7] | 康庄, 李辉, 孙丽萍, 等. 自由站立式立管总体设计与分析[J]. 船海工程, 2011, 40(5): 154–159. |
| [8] | ZHOU X K, DUAN M L, GU J J, et al.Numerical simulation and experimental investigation on the upper and lower assemblies of free standing hybrid riser system[C]//The 26th International Ocean and Polar Engineering Conference.[S.l.]:International Society of Offshore Polar Engineers, 2016:194-201. |
| [9] | HUANG K, DU D, SONG R X, et al.VIM of dual buoyancy can FSHR system[C]//The 23th International Offshore and Polar Engineering Conference.[S.l.]:International Society of Offshore and Polar Engineers, 2013:476-481. |
| [10] | 张辉, 柯珂, 王磊. 深水钻井作业管柱纵向振动载荷分析[J]. 石油机械, 2014, 42(4): 38–42. |
| [11] | 王德人. 求解非线性方程组的割线法[J]. 兰州大学学报(自科版), 1980(4): 29–42. |
| [12] | 季文美, 方同, 陈松淇. 机械振动[M]. 北京: 科学出版社, 1985: 347-351. |




