2. 北京工业大学;
3. 中国石油集团测井有限公司吐哈事业部
2. Beijing University of Technology;
3. Turpan-Hami Department of CNPC Logging Co., Ltd
0 引言
页岩气井压裂压力高、排量大、时间长,力-热耦合作用明显。前人在井筒完整性相关研究过程中,建立的力-热耦合模型主要是面向稠油热采井[1-6]或油管压裂,与页岩气水平井套管压裂工况存在显著差异。在威远-长宁页岩气井套损问题分析过程中,学者们就改造区域不对称、井筒环空束缚流体收缩及地层滑移等多项影响因素进行了分析[7-10],但均未对大规模压裂过程中力-热耦合作用下套管瞬态应力变化规律进行分析,且未分析排量对套管瞬态应力的影响。针对页岩气套管大规模压裂工程实际,笔者采用热流固耦合数值算法,对压裂过程中力-热耦合作用下套管的应力瞬态变化进行了计算,明确了力-热耦合作用下套管应力随压裂时间变化的规律,以及压裂排量对套管瞬态应力的影响。计算结果可为页岩气水平井压裂过程中套损问题分析提供参考。
1 压裂过程中水平段压裂液温度计算国内外专家学者所建立的温度场模型主要是基于油管压裂工程实际[11-14],与页岩气套管压裂差距较大。尹虎等[15]结合页岩气水平井压裂施工工艺及工况条件,建立了套管压裂温度场模型,但是未考虑压裂液与井壁之间的摩擦生热,以及压裂液排量对井筒温度场的影响。为此,笔者在考虑这2项因素的基础上,建立套管压裂过程中井筒温度场计算模型。建模时做如下假设:① 忽略地层间的纵向传热;② 井筒内流体径向温度相同,只沿轴向产生变化;③ 水平段远离井筒的边界温度为油藏中部的温度;④ 地层温度与深度呈线性关系,即Tz=Tb+α(z-b)。其中Tz表示地层某一点的温度,℃;Tb表示基准深度的温度,℃;α表示地温梯度,℃/m;z表示地层某一点的深度,m;b表示基准深度,m。
基于能量守恒方程建立井筒温度场模型,沿井筒轴向将井筒分成j等分,沿井壁到地层无限远处划分为i个区域。井筒内流体的能量守恒方程为:
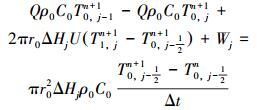
|
(1) |
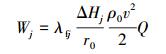
|
(2) |
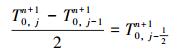
|
(3) |
式中:Wj为压裂液与井壁接触摩擦产生的热量,J。
与流体接触的套管单元的能量守恒方程为:
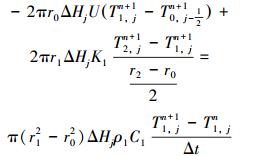
|
(4) |
其余固体单元的能量守恒方程为:
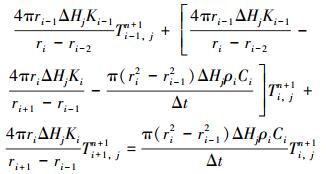
|
(5) |
式中:Q为压裂液排量,m3/min; ρ为密度,kg/m3;C为比热容,J/ (kg·℃);r为半径,m;ΔHj为单元体高度, m; U为流体与套管表面的对流传热系数,W/ (m2·℃);λfj为套管的摩阻系数,与流体雷诺数有关,无量纲;v为套管内流体的流速,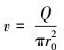
根据网格划分情况,i=0,1≤i≤n, n≤i≤m, m≤i≤k时,ρ、C分别代表压裂液、套管、水泥环及地层的密度和比热容,n、m、k分别代表划分的网格数,无量纲。
根据式(1)~式(4) 计算可得压裂过程中压裂液沿井筒温度的变化,并且可以计算出不同排量下水平段任意位置流经该处的、随时间变化的压裂液温度TlQ,将其作为条件参数输入到有限元模型中, 即:
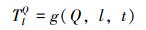
|
(6) |
式中:l代表井眼水平段某处到趾端的距离, m。
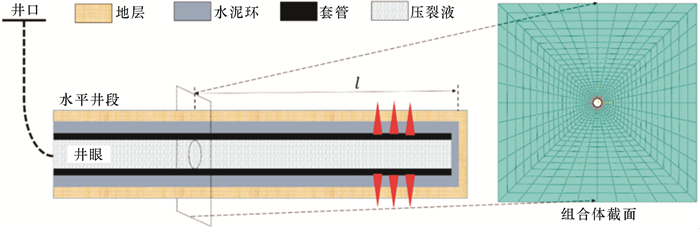
2 数值模型建立 2.1 数值模型假定套管、水泥环和地层在水平方向上均质,热、力学参数不发生变化,根据热传导及弹性力学理论,将相关问题简化为平面热传导和应力应变问题。基于圣维南定理,建立大小为3 m×3 m的二维数值模型,选择结构网格并采用变密度网格划分方式,以充分减小计算干扰。图 1为有限元模型及变密度网格划分图。
|
| 图 1 有限元模型和变密度网格划分图 Fig.1 Finite element model and graded meshing |
页岩气水平井压裂过程分为2个阶段:压裂阶段和压裂间歇阶段。在载荷和约束设置方面,整个压裂过程中无限远处地层为稳定热源,向组合体进行热传导。压裂阶段,压裂液与套管壁直接接触,压裂液、套管、水泥环及地层之间发生热交换,套管内壁承受的压力为施工泵压和静液柱压力之和;压裂间歇阶段,套管残存液体与套管不再发生热交换,组合体温度逐步回升,套管内壁承受的压力为压裂液静液柱压力。X和Y方向模型边界位移为0。
2.2 参数设置在参数设置方面,套管、水泥环和地层井眼几何及力学参数以页岩气井H3井实际参数为准,具体参数见表 1。H3井井深为3 320 m,井底温度为100 ℃,地面压裂液温度为20 ℃,施工泵压为82 MPa。压裂时间为4 h,压裂间歇时间为8 h。选用P110钢级、壁厚为12.14 mm的套管作为研究对象,地层最大水平和垂向主应力值分别为86和57 MPa。选取跟端处即水平段距离趾端lmax处作为研究对象,计算该处压裂液温度瞬态变化,得到TlQ=g(8,lmax, t), 0≤t≤4,将其作为计算参数输入到有限元模型中。
| 名称 | 外径/mm | 弹性模量/GPa | 泊松比 | 热传导系数/(W·kg-1·℃-1) | 比热容/(J·kg-1·℃-1) | 密度/(kg·m-3) | 热膨胀系数/(10-6℃-1) |
| 套管 | 127.00 | 210 | 0.30 | 45.00 | 461 | 7 800 | 13.0 |
| 水泥环 | 168.28 | 10 | 0.17 | 0.98 | 837 | 3 100 | 11.0 |
| 地层(井眼) | — | 22 | 0.23 | 1.59 | 1 256 | 2 600 | 10.5 |
3 力-热耦合作用对套管应力的影响 3.1 压裂过程中套管温度瞬态变化
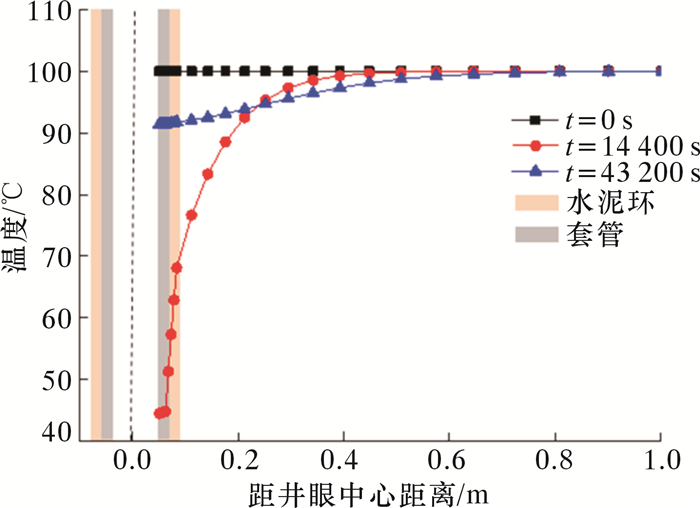
页岩气井套管压裂过程中,压裂液与套管内壁直接接触发生热交换,套管与水泥环、水泥环与地层发生热交换,套管-水泥环-地层组合体温度从内到外逐渐降低。图 2为压裂过程中不同时刻组合体温度径向分布。X轴零点处为井眼中线位置。由图 2可知,初始时刻(t=0 s)套管、水泥环与地层温度保持一致。压裂阶段末(t=14 400 s),套管、水泥环与地层温度在径向上出现不同幅度的下降,表现为:① 套管温度降低幅度最大,内、外壁几乎不存在温差,主要是因为金属导热性较好;② 水泥环次之,内、外壁温差较为明显;③ 地层温度降低幅度最小,只在近井眼处(<0.8 m)存在显著温差,距离井眼越远,温度变化越不明显。压裂间歇期结束时(t=43 200 s)组合体温度整体上升,套管内壁到地层温度均有不同程度的升高。
|
| 图 2 压裂过程中不同时刻组合体温度径向分布图 Fig.2 Radial distribution of the temperature of the combined body at different times during the fracturing operation |
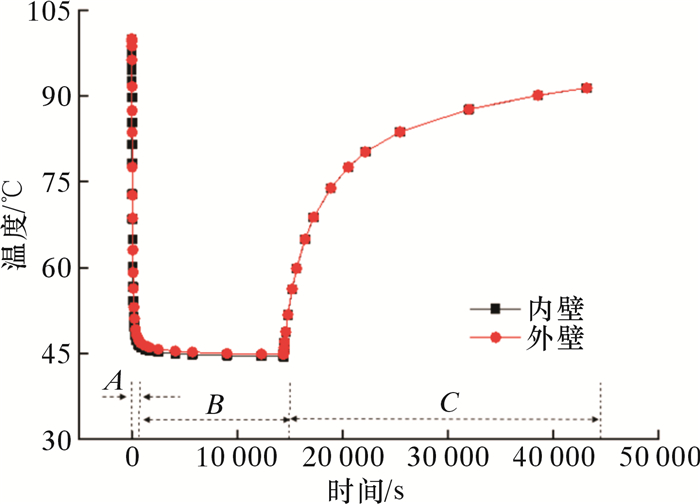
选择排量为8 m3/min作为基础计算条件,开展页岩气井压裂过程中套管温度瞬态变化规律研究。图 3为压裂过程中套管内、外壁温度瞬态变化曲线。
|
| 图 3 压裂过程中套管内、外壁温度瞬态变化曲线 Fig.3 Transient temperature change of the inner and outer wall of the casing during the fracturing operation |
由图 3可知,压裂过程中套管温度变化可以划分为A、B、C 3个阶段,分别为迅速降温段、低温保持段以及温度回升段。压裂液进入套管后,套管的内、外壁温度迅速下降,不存在显著温度差异。在短时间内下降至近恒值温度最低值,然后在压裂过程中几乎保持该温度不变(变化值<2 ℃)。定义该近恒值温度为Tmin,Tmin是随时间变化的变值。压裂结束后在地温的影响下套管温度逐步上升,其中外壁温度先升高,内、外壁之间不存在显著差异。
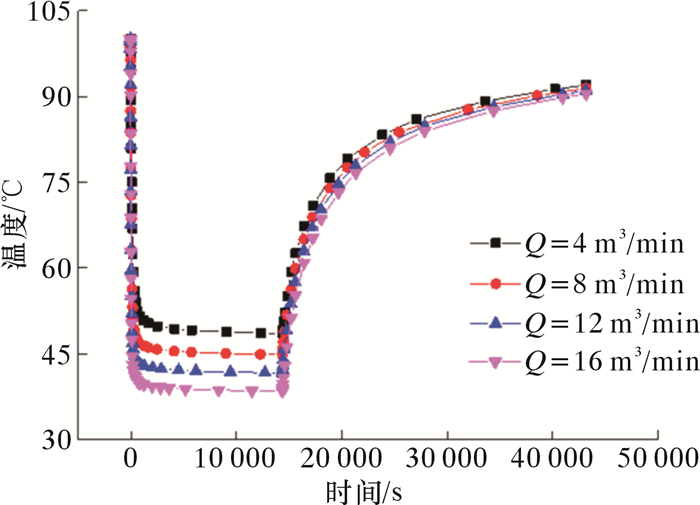
为了获得最大增产改造体积,压裂时往往采用不同排量进行作业,导致套管瞬态温度变化发生改变。选择套管内壁作为研究对象,对压裂过程中不同排量下温度瞬态变化规律进行研究。图 4为不同排量下压裂过程中套管内壁温度变化曲线。由图可知,不同排量下套管内壁温度变化趋势较为相似,迅速降温段、低温保持段以及温度回升段时间域长没有明显差异。但是Tmin值与排量大小存在显著关系,排量越大,套管压裂过程中的Tmin值就越低。压裂结束后,时间相同时,排量越大,套管内壁回升达到的温度就越低。
|
| 图 4 不同排量下压裂过程中套管内壁温度变化曲线 Fig.4 Temperature change of the casing inner wall during the fracturing operation under different displacement |
3.2 力-热耦合作用下套管应力瞬态变化
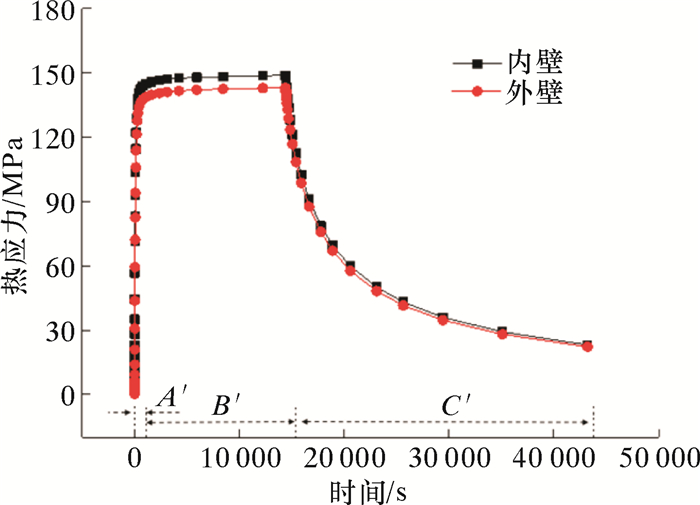
为了研究不同排量下力-热耦合作用对套管应力的影响规律,首先对特定排量(Q=8 m3/min)下套管热应力瞬态变化规律进行研究。图 5为压裂过程中套管内、外壁热应力变化曲线。由图 5可知,压裂过程中套管内、外壁温度先升高,然后保持近恒值,最后降低。热应力变化可以划分为A′、B′和C′ 3个阶段,分别是热应力迅速增大段、高热应力保持段以及热应力降低段,与温度变化的3个阶段正好对应。
|
| 图 5 压裂过程中套管内、外壁热应力变化曲线 Fig.5 Thermal stress change of inner and outer wall of the casing during fracturing operation |
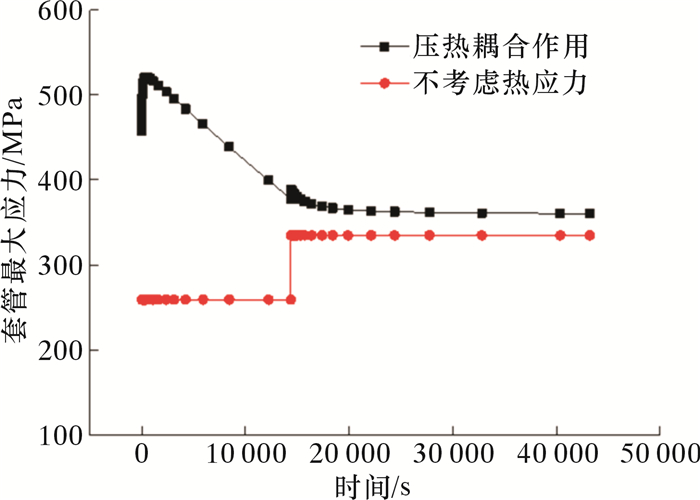
就套管内、外壁相比较,内壁温度变化最大,热应力也较大,因此选择套管内壁作为研究对象。图 6为考虑(不考虑)热应力时套管内壁应力瞬态变化曲线。由图可知:① 在压裂阶段,套管内壁最大应力先快速提高后降低。该阶段套管内压为施工泵压和压裂液静液柱压力之和,套管处于受拉状态。压裂液进入后井筒内液体与套管内壁直接接触,造成套管内壁表面陡峭的温度梯度,应力迅速增大。随着热传导的进行,套管内壁表面温度不断降低,温度梯度也随之下降,表面所受应力逐渐减小。套管应力最大值出现在压裂初期465 s。② 在压裂间歇阶段,套管内壁最大应力先小幅上升,然后开始缓慢下降。该阶段套管内压为压裂液静液柱压力,套管处于受压状态。停泵导致套管应力出现拉压变化,最大应力位置发生跃迁,套管应力数值先小幅上升。在无限远处地层热传导作用下,组合体温度不断升高,套管内外壁温度不断提升,内壁应力不断减小,最后趋于稳定,由于套管未恢复到压裂前的温度,残余应力导致最终套管内壁应力要比不考虑力-热耦合作用时大。
|
| 图 6 考虑热应力时套管内壁应力瞬态变化曲线 Fig.6 Transient stress change of the casing inner wall considering (not considering) the thermal stress |
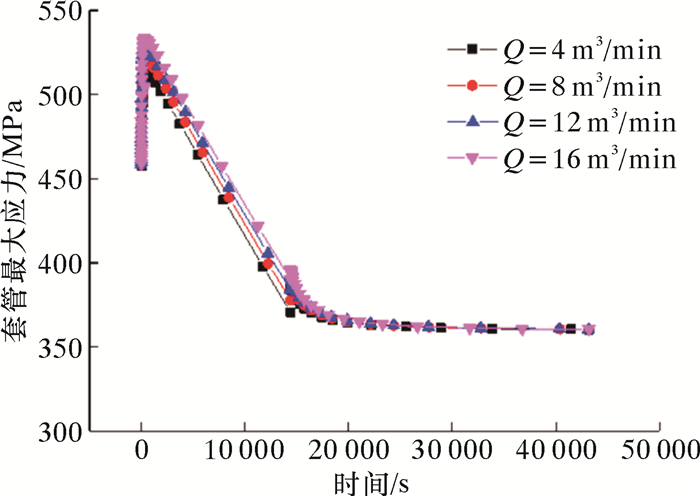
图 7为不同压裂排量下套管内壁最大应力曲线。由图可知,不同排量下套管内壁最大应力变化趋势较为一致,套管内壁最大应力均是在压裂初期达到最大。压裂过程中,排量越大,套管的最大应力也越大,进而使套损发生的风险也就越大。
|
| 图 7 不同压裂排量下套管内壁最大应力曲线 Fig.7 Maximum stress curve of the casing under different fracturing displacement |
4 结论
(1) 在考虑摩擦生热以及排量对井筒温度影响的基础上,建立了压裂过程中井筒温度场模型,明确了压裂过程中套管温度瞬态变化规律,即先迅速降低,然后保持接近恒值Tmin,压裂结束后逐步回升;压裂过程中排量越大,恒值Tmin越低。
(2) 基于热流固数值算法,建立了套管-水泥环-地层有限元模型,对压裂过程中力-热耦合作用下套管内壁最大应力瞬态变化规律进行了研究。研究结果表明:压裂过程中套管应力先升高后降低,最大应力出现在压裂初期;排量越大,套管内壁最大应力值越大,同等条件下产生套损的风险也就越大。
| [1] | 李静, 林承焰, 杨少春, 等. 套管-水泥环-地层耦合系统热应力理论解[J]. 中国石油大学学报(自然科学版), 2009, 33(2): 63–69. |
| [2] | 陈延. 稠油热采井套管保护技术研究[J]. 特种油气藏, 2007, 14(6): 83–86. |
| [3] | 余中红, 檀德库, 郑成立, 等. 齐40块蒸汽驱井组油层套管应力数值计算[J]. 特种油气藏, 2002, 15(1): 99–102. |
| [4] | 陈勇, 练章华, 陈敏, 等. 水泥环周向缺失的热采井井筒热应力耦合分析[J]. 石油钻采工艺, 2008, 30(2): 108–110. |
| [5] | 刘坤芳, 张兆银, 孙晓明, 等. 注蒸汽井套管热应力分析及管柱强度设计[J]. 石油钻探技术, 1994, 22(4): 36–61. |
| [6] | 宋洵成, 赵洪山, 管志川. 稠油热采井套管的预应力分析[J]. 石油钻采工艺, 2006, 28(4): 64–67. |
| [7] | 田中兰, 石林, 乔磊. 页岩气水平井井筒完整性问题及对策[J]. 天然气工业, 2015, 35(9): 70–77. |
| [8] | LIAN Z H, YU H, LIN T J, et al. A study on casing deformation failure during multi-stage hydraulic fracturing for the stimulated reservoir volume of horizontal shale wells[J]. Journal of Natural Gas Science and Engineering, 2015, 23(1): 540–546. |
| [9] | 范明涛, 柳贡慧, 李军, 等. 页岩气井温压耦合下固井质量对套管应力的影响[J]. 石油机械, 2016, 44(8): 1–5. |
| [10] | DANESHY A A.Impact of off-balance f racturing on borehole stability & casing failure[R].SPE 93620, 2005. |
| [11] | WOOLEY G R. Computing downhole temperatures in circulation, injection, and production wells[J]. Journal of Petroleum Technology, 1980, 32(9): 1509–1522. DOI: 10.2118/8441-PA |
| [12] | 卢德唐, 曾亿山, 郭永存. 多层地层中的井筒及地层温度解析解[J]. 水动力学研究与进展, 2002, 17(3): 382–390. |
| [13] | RAMER H. Wellbore heat transmission[J]. Journal of Petroleum Technology, 1962, 14(4): 427–435. DOI: 10.2118/96-PA |
| [14] | 王鸿勋, 李平. 水力压裂过程中井筒温度的数值计算方法[J]. 石油学报, 1987, 8(2): 91–99. DOI: 10.7623/syxb198702012 |
| [15] | 尹虎, 张韵洋. 温度作用影响套管抗挤强度的定量评价方法——以页岩气水平井大型压裂施工为例[J]. 天然气工业, 2016, 36(4): 73–77. DOI: 10.3787/j.issn.1000-0976.2016.04.011 |



