2. 南京市锅炉压力容器检验研究院
2. Nanjing Boiler and Pressure Vessel Inspection Institute
0 引言
随着石化行业生产规模的大型化,以管壳式换热器为代表的单体设备日趋大型化,壳程流速不断增大,折流板之间间距逐渐变大,削弱了换热管管束的刚度,从而使管束振动成为换热器损坏的重要原因。理论上换热管能在所有频率下因流体流动而激起振动[1],因此只有全面研究换热管的固有频率特性,使激励频率远离固有频率,才能避免流体诱发振动时出现共振现象,保证换热器的安全运行。
随着材质、外径、壁厚、折流板间距和节径比的变化,换热管固有频率会相应地变化[2]。刘明等[3]的研究表明,换热管充满介质以后,其振型保持不变但固有频率会减小;周宁波[4]通过模态特性研究发现,外界流场的变化对换热管在流体环境中的固有振动特性的影响很小;郭建英等[5]探讨了低翅片换热管固有频率的计算方法,得出基于Rayleigh-Ritz法的计算方法计算精度较高的结论;聂清德等[6]对多跨U形管的最低固有频率的计算表明,跨数对固有频率影响较大;G.N.XI等[7]分析了结构、温度及流场对4种换热管固有频率的影响;马腾飞[8]通过数值模拟结合试验得到了翅片几何参数对双金属翅片管固有频率的作用规律。
换热器实际运行时,管、壳程的温度差及压力差会在换热管内产生较大的轴向应力,从而影响换热管的刚度并改变其固有频率。王珂等[9]针对某换热器提出了精细有限元模型和简化模型,研究了温度应力对该换热器管束振动特性的影响。而关于轴向力对换热管固有频率的影响系统性的研究较少。鉴于此,笔者在简化有限元模型的基础上[10],采用瞬态激振与傅里叶变换相结合的方法对轴向力作用下的等长多跨换热管固有频率进行计算,分析了不同轴向力作用下的1~3阶固有频率及轴向力影响因素,从而得到轴向力对换热管固有频率的影响规律。
1 轴向力作用下固有频率计算方法 1.1 TEMA标准计算方法TEMA标准中提出了一种简化算法,将多跨换热管简化为多个单跨管,分别计算其固有频率,并取最小频率作为换热管的1阶固有频率。考虑计算简便,对公式进行单位变换,计算公式如下:
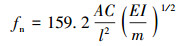
|
(1) |
式中:C为依赖于边界条件的常数;E为管子弹性模量,Pa;I为管子截面弹性矩,m4;l为管子跨长,m;m为考虑管内、外流体的单位长度换热管质量,kg/m;A为轴向力影响系数,计算式如下。
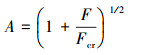
|
(2) |
式中:F为轴向力,N;Fcr为临界稳定压力,Fcr=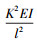
GB151—2014的附录C中,给出了轴向力作用时直管固有频率fna的计算公式。公式如下:
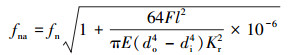
|
(3) |
式中:Kr为与管段固定条件有关的系数;fn为未受轴向力作用下的固有频率,Hz。
对比不难发现,TEMA计算公式中的临界稳定压力Fcr即为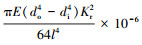
笔者采用的ANSYS瞬态分析又称为时间历程分析,能够计算出结构受动态作用情况下的位移、应变和应力等随时间的变化[12],其通用运动方程为:
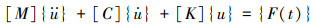
|
(4) |
式中:[M]、[C]、[K]分别代表结构体系的质量、阻尼和刚度矩阵;{F(t)}是作用在结构中的动态载荷;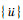
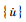
采用ANSYS瞬态分析方法可以计算出结构在受到激振后的时间响应历程,通过激振响应进行傅里叶变化,从而计算系统的固有频率,其原理为:
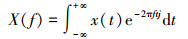
|
(5) |
式中:X(f) 为计算所得频谱;x(t) 为振动时间位移函数;f为频率,Hz;t为时间,s。
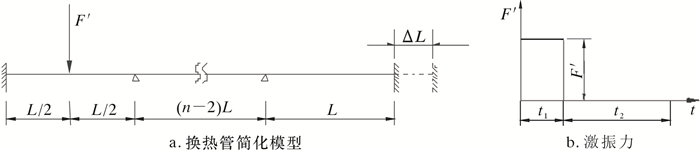
瞬态计算模型简图如图 1所示。采用瞬态分析的方法对换热管的固有频率计算时,采用梁单元BEAM189对换热管进行简化,换热管两端为固支,中间折流板处支撑简化为简支,在第1跨中点处施加一个t1时间的矩形激振力F′(见图 1b),并计算之后t2时间内的系统振动响应,即可得出换热管振动响应的时域图。当换热管需要考虑轴向力影响时,可以在换热管的一端施加一个轴向位移ΔL来模拟其所受的轴向力 (见图 1a)。
|
| 图 1 瞬态计算模型简图 Fig.1 Transient calculation model diagram |
2 轴向力作用下换热管固有频率计算
选用尺寸为ø25 mm×2 mm、跨距l=1.0 m的等跨距碳钢管进行不同跨数与不同轴向力作用下的固有频率变化研究。换热管弹性模量E=2.01×105 MPa,泊松比μ=0.3。为定性分析轴向力对换热管固有频率的影响,不计入管内、外介质对于换热管固有频率的影响,换热管密度ρ=7 850 kg/m3。
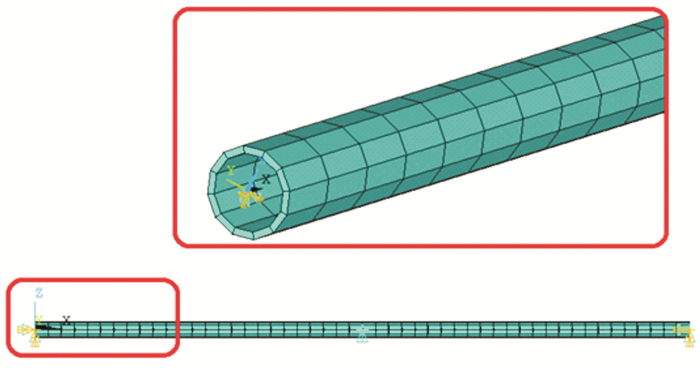
2.1 单跨管与2跨管的固有频率分析通过选择ANSYS软件中3节点梁单元BEAM189单元对换热管进行建模,计算模型如图 2所示。在折流板处施加UY和UZ方向约束,换热管与管板连接处施加全约束。根据瞬态模拟的方法对单跨管与等长2跨管在轴向力从-10 kN到10 kN作用下的固有频率进行计算。
|
| 图 2 2跨管计算模型 Fig.2 Calculation model of the two-span tube |
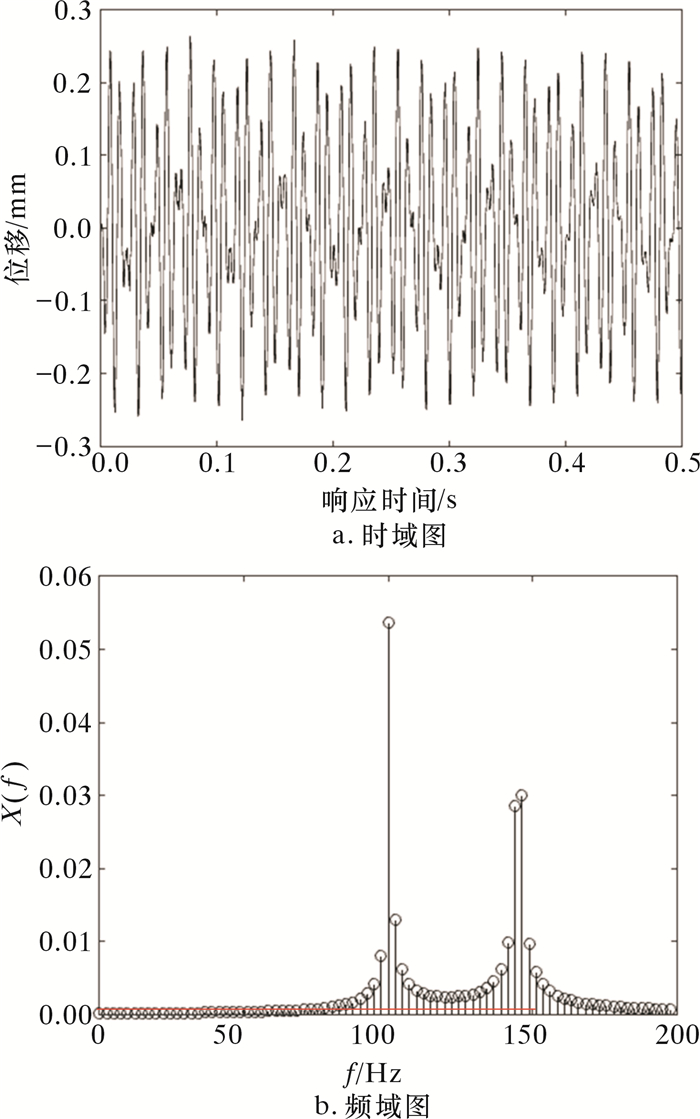
无轴向力时2跨管计算结果见图 3。依据瞬态计算的时间位移结果,采用快速傅里叶变换及加Hanning窗比值校正法处理结果[13-14]。同时根据TEMA标准对单跨管与2跨管的固有频率进行计算,并将结果与有限元计算结果进行对比 (见表 1)。
|
| 图 3 无轴向力时2跨管计算结果 Fig.3 Calculation results of the two-span tube without axial force |
| 跨数 | 轴向力/kN | 模拟计算结果/Hz | TEMA计算结果/Hz | 差值/% |
| 单跨管 | 10 | 154.275 3 | 156.092 4 | 1.16 |
| 5 | 149.866 7 | 151.481 7 | 1.07 | |
| 0 | 145.611 2 | 146.726 3 | 0.76 | |
| -5 | 140.572 5 | 141.811 4 | 0.87 | |
| -10 | 135.651 9 | 136.720 0 | 0.78 | |
| 2跨管 | 10 | 112.450 1 | 113.427 6 | 0.86 |
| 5 | 106.682 2 | 107.459 9 | 0.72 | |
| 0 | 100.550 2 | 101.140 8 | 0.58 | |
| -5 | 93.977 9 | 94.399 5 | 0.45 | |
| -10 | 86.869 2 | 87.138 4 | 0.31 |
由表 1可知, 随着换热管轴向力减小,其固有频率也在减小。单跨管在轴向力为-10 kN时,与无轴向力相比其固有频率仅下降了7%,在相同轴向力条件下,2跨管的固有频率下降了13.6%。由此可见,不同的支撑形式对于管束的应力刚化与软化作用存在着影响。对比瞬态计算结果与TEMA标准计算值,两者差距约为1%。综上,TEMA标准对单跨管在两端固支与一端固支2端简支2种支撑条件下的固有频率计算较为精确。
2.2 多跨管的固有频率分析采用有限元模拟计算方法分别对l=1.0 m,等长3跨管、4跨管和5跨管在不同轴向力作用下的前3阶固有频率进行计算,结果如图 4所示。
|
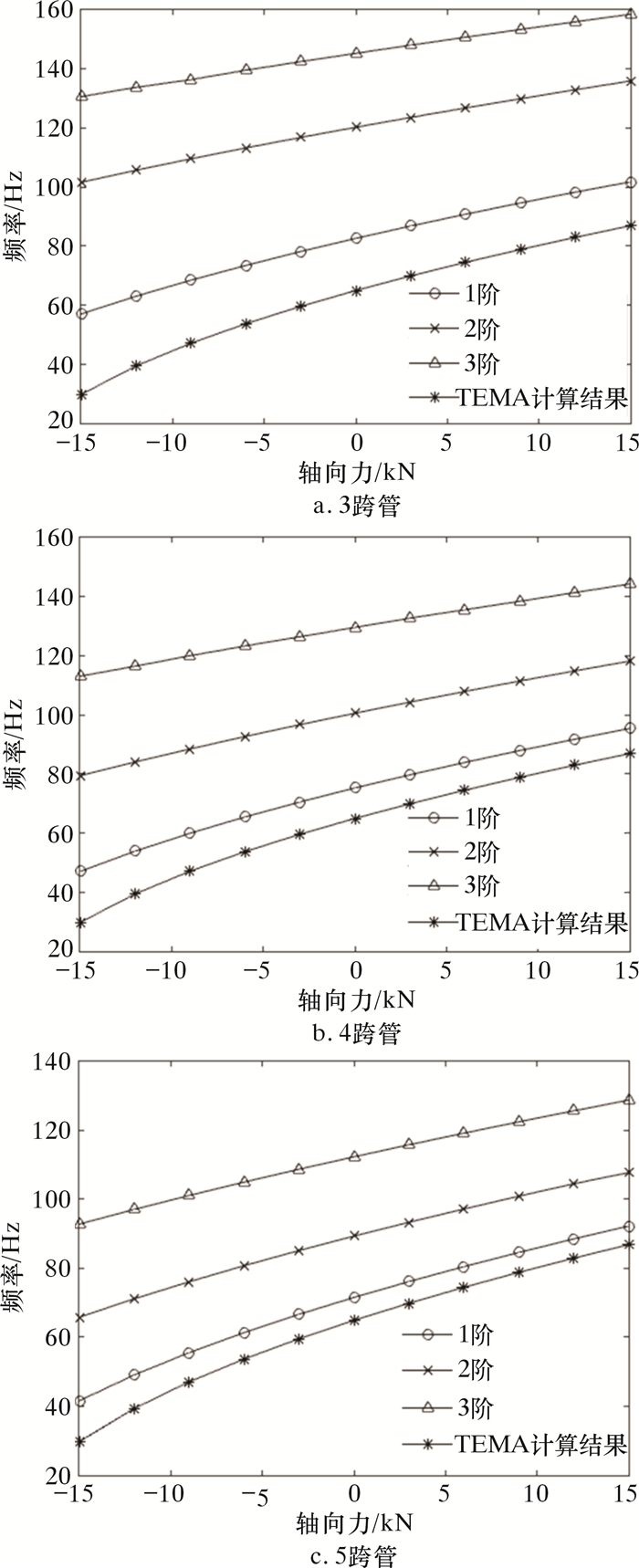
| 图 4 不同轴向力作用下固有频率 Fig.4 Natural frequency under different axial forces |
由计算结果可知:在轴向拉应力作用下,由于应力刚化作用,换热管的固有频率不断升高;在轴向压应力作用下,由于应力软化作用,换热管的固有频率不断降低。对于等长3跨管,当轴向拉力为15 kN时,其频率上升19.150 Hz,升高了23.2%;当轴向压应力为15 kN时,其频率下降了25.597 Hz,约下降了30.1%。压应力对换热管的应力软化作用明显强于等值拉应力作用下的应力刚化效果,当换热管承受较大轴向压力时,其对于固有频率的降低作用不能忽视。
随着换热管跨数的增多,其2阶固有频率与3阶固有频率逐渐向1阶固有频率靠近。在5跨管中,1阶和2阶固有频率相差仅20 Hz左右。在15 kN轴向压应力作用下,其2阶固有频率下降65.823 Hz,已小于其在无轴向力作用下的1阶固有频率71.577 Hz。因此在轴向力较大的情况下,计算多跨换热管频率时,仅考虑换热管1阶固有频率太片面,轴向力对换热管2阶频率的降低作用也应该被考虑。
纵观图 4可知,对于等长3跨管、4跨管与5跨管,TEMA标准的固有频率计算均相等,且明显小于ANSYS模拟计算的1阶固有频率。这主要是因为TEMA在计算时将多跨管简化为多个单跨管,根据各自的支撑情况进行计算,并未考虑管段之间的相互影响[15]。随着跨数的增多,两端简支段的数量增加,其对频率的影响也逐渐增大,等跨换热管的1阶固有频率越来越趋近于TEMA公式计算值。
2.3 多跨管轴向力影响因素分析根据TEMA标准的固有频率计算公式 (1) 可知,换热管轴向力影响系数A体现了轴向力对于换热管固有频率的影响。当l=1.0 m,一端固支一端简支时临界稳定压力为38 801.4 N,两端简支时为18 976.4 N。分别计算3跨管、4跨管和5跨管在轴向力-15~15 kN下前3阶轴向力影响系数,结果如图 5所示。
|
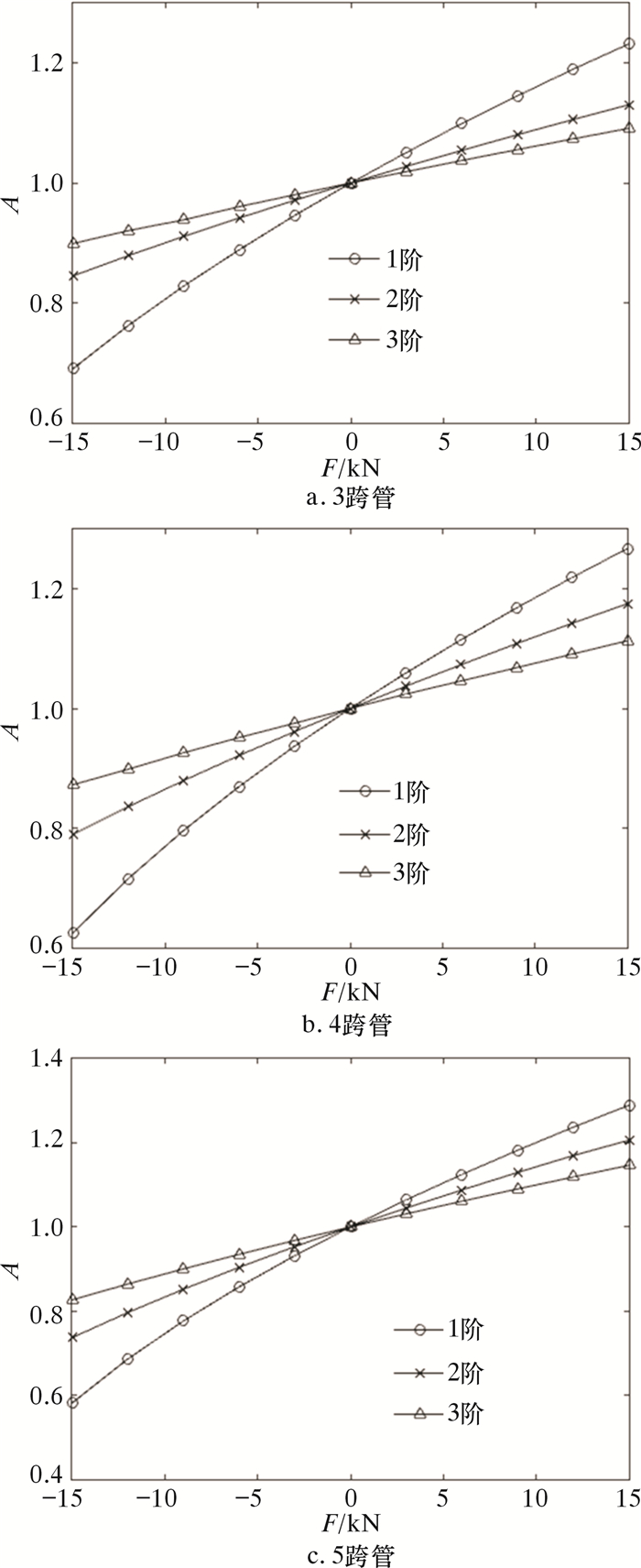
| 图 5 不同轴向力作用下换热管前3阶轴向力影响系数 Fig.5 The first third order axial force influence coefficient of the heat transfer tube under different axial forces |
由图 5可以看出,前3阶固有频率的轴向力影响系数A随着轴向力的变化趋势基本一致,随着轴向力的减小,轴向力影响系数A也在不断减小。对于3跨管,当轴向力为-15 kN时,1阶轴向力影响系数为0.690,2阶轴向力影响系数为0.845,3阶轴向力影响系数为0.899。由此可见,轴向力对1阶固有频率影响较大,随着固有频率阶数的升高,其影响逐渐减小。
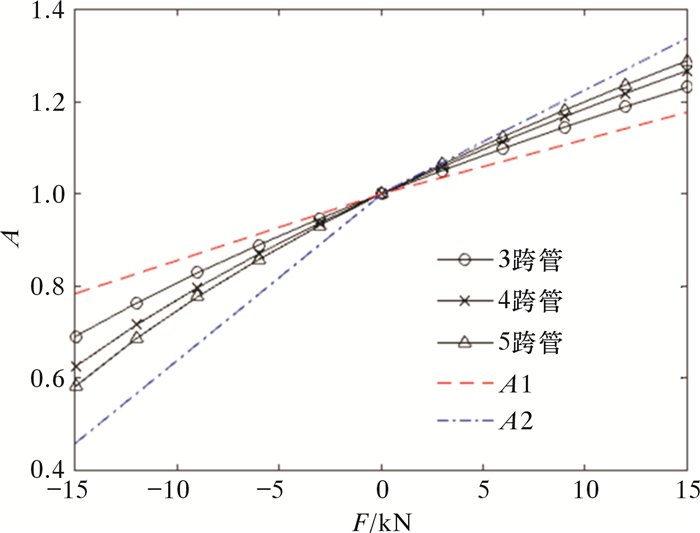
有限元计算与TEMA计算1阶轴向力影响系数对比如图 6所示。图中:A1为l=1.0 m、一端固支一端简支换热管的轴向力影响系数变化曲线,A2为l=1.0 m、两端简支的换热管轴向力影响系数变化曲线。相同轴向力作用时,5跨管的A值离A1最远,即与无轴向力作用时固有频率差距最大,其次为4跨管、3跨管。对此可以理解为对于跨距相等的多跨换热管,随着跨数的增多,轴向力对固有频率的影响越来越明显。由于简支段与两端相互作用,多跨管的1阶轴向力影响系数A处于A1与A2之间。随着跨数的增多,简支段对于整体频率的影响越来越大,轴向力影响系数A逐渐向A2靠近。因此在多跨管固有频率计算中,采用两端简支轴向力影响系数进行计算会引起计算结果偏于保守。
|
| 图 6 有限元与TEMA计算1阶轴向力影响系数对比 Fig.6 Comparison of influence coefficients of the first order axial force by FEM and TEMA |
3 结论
(1) 换热管在承受轴向应力时,其刚度会发生变化进而引起固有频率发生变化,当轴向力为拉应力时,换热管受到应力刚化作用,固有频率升高;当轴向力变为压应力时,换热管受到应力软化作用,固有频率降低,并且拉应力的应力刚化效果要小于等值压应力的应力软化效果。
(2) 轴向力对于换热管1阶固有频率影响较大,对于2阶、3阶固有频率的影响逐渐减小。随着换热管跨数的增多,1阶与2阶固有频率之间的差距逐渐减小,当轴向压应力较大时,2阶固有频率仍有可能会低于无轴向力作用下的1阶固有频率,因此在多跨换热管设计时,轴向力对于2阶固有频率也应当被考虑。
(3) 对于跨距相等的多跨换热管,随着跨数的增多,轴向力对于固有频率的影响越来越明显,而轴向力影响系数A介于一端固支一端简支与两端简支轴向力影响系数之间,随着换热管两端简支段的增多,其在固有频率中的影响逐渐增大,轴向力影响系数逐渐向两端简支时轴向力影响系数趋近。
| [1] | 聂清德, 谭蔚. 管壳式换热器流体诱发振动[M]. 北京: 中国石化出版社, 2014. |
| [2] | 赖永星. 换热器管束动态特性分析及流体诱导振动研究[D]. 南京: 南京工业大学, 2006. |
| [3] | 刘明, 张应迁, 柳忠彬, 等. 换热管振动特性研究[J]. 机床与液压, 2013, 41(11): 61–63. DOI: 10.3969/j.issn.1001-3881.2013.11.016 |
| [4] | 周宁波. 脉动流作用下换热器管束的振动特性研究[D]. 武汉: 武汉工程大学, 2013. |
| [5] | 郭建英, 王亮清. 低翅片换热管固有频率计算方法探讨[J]. 石油化工设备, 2006, 35(5): 27–29. |
| [6] | 聂清德, 谭蔚, 吴皓. 多跨U形管的最低固有频率[J]. 化工设备与管道, 2011, 48(5): 17–21. |
| [7] | XI G N, SHI C, ZOU S, et al. Research progress in natural frequency calculation of heat exchanger tube bundles[J]. Applied Mechanics & Materials, 2014, 672: 1592–1595. |
| [8] | 马腾飞. 双金属换热管固有振动模态的研究[D]. 太原: 太原理工大学, 2016. |
| [9] | 王珂, 赖永星, 王贺郑. 温度应力对换热器管束动特性的影响分析[J]. 石油机械, 2007, 35(3): 16–18. |
| [10] | 苏文献, 陈功. 换热管固有频率计算方法[J]. 上海理工大学学报, 2015, 37(6): 535–539. |
| [11] | 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 热交换器: GB/T 151-2014[S]. 北京: 中国标准出版社, 2015. |
| [12] | 谢龙汉, 刘新让, 刘文超. ANSYS结构及动力学分析[M]. 北京: 电子工业出版社, 2012. |
| [13] | 闻邦椿. 机械振动理论及应用[M]. 北京: 高等教育出版社, 2009. |
| [14] | 丁康, 谢明, 杨志坚. 离散频谱分析校正理论与技术[M]. 北京: 科学出版社, 2008. |
| [15] | 聂清德, 段振亚, 谭蔚, 等. 关于TEMA标准《流体诱发振动》若干问题的讨论 (一)[J]. 压力容器, 2004, 21(12): 1–5. DOI: 10.3969/j.issn.1001-4837.2004.12.001 |




