2. 胜利石油工程有限公司钻井工艺研究院
2. Drilling Technology Research Institute, Shengli Petroleum Engineering Co., Ltd
0 引言
目前,海洋钻井已逐步迈向深水、超深水。为了解决深水钻井遇到的地层压力窗口较窄等一系列难题,国外20世纪90年代开发了双梯度钻井系统。该系统根据原理不同分为海底泵举升和双密度钻井2种。其中海底泵举升钻井(SMD)分为海水驱动隔膜泵、电力驱动离心泵和电潜泵3种[1]。双密度钻井按照注入流体的不同又分为注空心球、注气和注低密度流体3种。
与海底泵举升钻井相比,注空心球双密度钻井具有对常规钻井设备改动小,不使用海底泵,减少了海底装置的数量,产生压力梯度呈线性等特点[2-3]。此外,空心球可分离回收重复使用,有效降低了钻井成本,在中等深度水深(600~1 500 m)有较好的应用前景。近年来,使用空心玻璃微球(hollow glass microspheres,简称HGS)来降低钻井液和固井水泥浆密度的方法,已在石油和采矿工业得到越来越多的应用[4]。
我国在空心球双密度钻井方面的研究基本处于空白阶段,为推进我国深水钻井技术发展,有必要开展空心球双密度钻井技术研究。
1 技术分析 1.1 工作原理空心球价格高,直径小,如何有效地注入、分离和循环使用是实现注空心球双密度钻井的技术瓶颈[5]。空心球注入循环过程如图 1所示。从图可以看出,注入阀是其中的关键设备,决定了空心球双密度钻井能否成功应用。

|
| 图 1 空心球注入循环示意图 Fig.1 HGS injection cycle diagram |
1.2 结构参数
注入阀采用水力旋流器,可有效分离携带液,并将空心球注入钻井液,经隔水管环空或者返回管线返回[6]。选择水力旋流器的依据为:① 处理的矿浆体积Q;② 分级粒度(或溢流最大粒度)d。
根据Q和d确定旋流器的直径D。采用直径为2~3 mm空心球,参考JB/T 9035—1999水力旋流器手册,选用FX-180旋流器。因旋流器工作水深为1 500 m,此时出口压力约为15 MPa,旋流器处理能力通过公式计算:
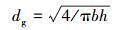
|
(1) |
式中:dg为进口当量直径,cm;b为进口宽度,cm;h为进口高度,cm。
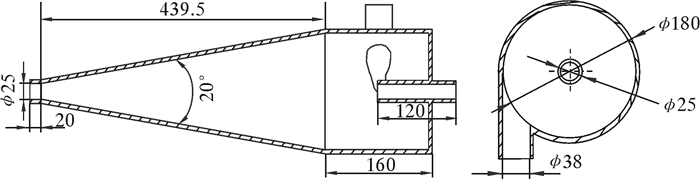
注入阀结构示意图如图 2所示。其公称直径D=180 mm,锥角α=20°,结构参数为:进口直径di=38 mm,溢流管直径do=25 mm,底流管直径du=25 mm,圆柱筒长度Ld=160 mm,旋流腔长度Ls=439.5 mm,尾部直管段长度Lu=20 mm。
|
| 图 2 注入阀结构示意图 Fig.2 Structural schematic diagram of injection valve |
当压力p大于或小于0.1 MPa时,处理能力为
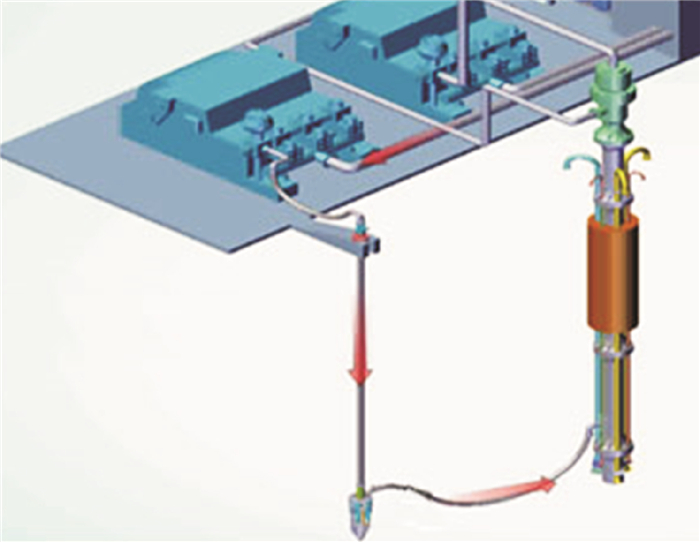
基于海洋平台固控系统,采用SolidWorks软件建立空心球水下注入阀(见图 3)和注入系统(见图 4)整体三维模型。

|
| 图 3 注入阀三维模型 Fig.3 Three-dimensional model of injection valve |
|
| 图 4 空心球注入系统三维模型 Fig.4 Three-dimensional model of HGS injection system |
2 力学模型
目前主要有欧拉-欧拉和欧拉-拉格朗日2种数值计算的方法处理多相流问题。其中欧拉-拉格朗日方法是轨道模型或离散相的方法,欧拉-欧拉方法可以分为3种多相流模型:VOF模型、混合(Mixture)模型以及欧拉(Eulerian)模型[7-8]。混合模型和欧拉模型适用于流动中有相混合或分离或分散相的体积分数超过10%的情形,此处选用计算精度较高的欧拉模型进行计算。
圆盘泵内固液两相流动属于湍流流动,湍流模型采用RNG(renormalization group)κ-ε模型。固液两相数值模拟时定义液相为基本相,固相颗粒为第2相,假设固相和液相均作为连续介质存在于流场中,固液两相流动采用欧拉模型方程描述。
液相连续性方程及动量方程分别为:
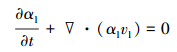
|
(2) |

|
(3) |
式中:αl为液相体积分数;t为时间,s;vl为液相速度,m/s;ρl为液相密度,kg/m3;p为两相共享的压力,Pa;τl为液相应变-应力张量;g为重力加速度,m/s2;Fsl为固相对液相的作用力。
固相连续性方程及动量方程分别为:
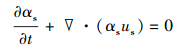
|
(4) |
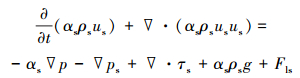
|
(5) |
式中:αs为固相体积分数;us为固相速度,m/s;ρs为固相密度,kg/m3;ps为固相压力,Pa;τs为固相相应应变-应力张量;Fls为液相对固相的作用力,且Fls=-Fsl。
两相的体积分数方程为:
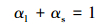
|
(6) |
湍流能κ方程及湍流耗散率ε方程分别为:
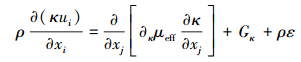
|
(7) |
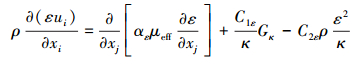
|
(8) |
式中:κ为湍动能,m2/s2;ακ为模型系数,ακ=1.39;Gκ为由平均速度引起的湍动能κ产生项;ε为湍动能耗散率,m2/s2;αε为模型系数,αε=1.39;G1ε为Gκ项模型系数,G1ε=1.46;G2ε为ε项模型系数,G2ε=1.68。
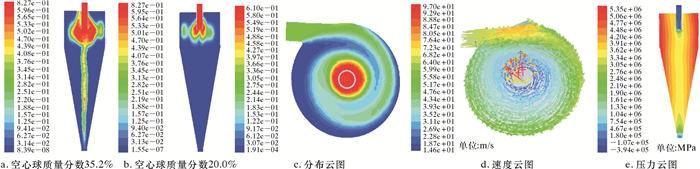
3 模拟计算携带液可采用海水或特定基液,使用海水的优点是海水可直接排放到海洋中,不会稀释隔水管内的钻井液,缺点是增加海底注射泵装备。使用特定基液的优点是易实现空心球在钻井液中的高质量分数(40%~60%),携带液体也容易实现回收利用,缺点是需要2条附加管线。采用Fluent软件模拟计算分离效果,算例中采用直径2.5 mm的空心球,携带液分别使用海水和基液。携带液使用海水时,空心球分布和分离效率如图 5和表 1所示。表中w为空心球质量分数,m球为空心球质量流量,m水为海水质量流量,η为空心球分离效率。
|
| 图 5 携带液为海水时空心球分布情况 Fig.5 Distribution of HGS while applying seawater as the carrier liquid |
| w/% | 35.2 | 20.0 | 15.0 | 10.0 |
| 入口m球/(kg·s-1) | 13.10 | 13.10 | 13.10 | 13.10 |
| 底部出口m球/(kg·s-1) | 3.63 | 0.66 | 0.43 | 0.04 |
| 上部出口m球/(kg·s-1) | 9.37 | 12.44 | 12.53 | 12.54 |
| 入口m水/(kg·s-1) | 24.09 | 52.40 | 74.25 | 131.35 |
| 底部出口m水/(kg·s-1) | 17.35 | 36.99 | 59.73 | 83.65 |
| 上部出口m水/(kg·s-1) | 6.61 | 15.09 | 14.23 | 48.66 |
| 携带液为海水时η/% | 71.55 | 94.95 | 95.64 | 95.72 |
从表 1可以看出,空心球体积分数越大,分离效率越低,当体积分数为50.0%,即质量分数为35.2%时,第1级分离效率为71.55%,溢流口空心球和海水的质量流量分别为9.37 kg/s和6.61 kg/s,该混合物空心球体积分数为72.27%;当体积分数为31.5%,即质量分数为20.0%时,第1级分离效率达94.95%,溢流口空心球和海水的质量流量分别为12.44 kg/s和15.09 kg/s,该混合物的空心球的体积分数为60.26%。当体积分数为24.5%,即质量分数为15.0%时,第1级分离效率为95.64%,溢流口空心球和海水的流量分数分别为12.83 kg/s和14.23 kg/s。当体积分数为15.5%,即质量分数为10.0%时,第1级分离效率为95.72%,溢流口空心球和海水的质量流量分别为12.54 kg/s和48.66 kg/s。
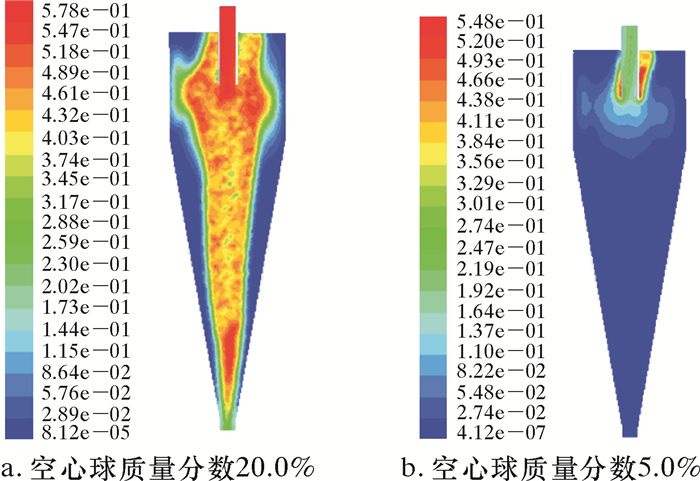
使用油基钻井液时,推荐采用基液携带空心球,基液携带空心球直接注入隔水管可能导致钻井液内基液过多,为控制基液的进入,可将携带空心球的基液混合物通过水下旋流器分离,进一步提高空心球的体积分数,满足钻井需要。携带液使用基液时,空心球分布和分离效率如图 6和表 2所示。
|
| 图 6 携带液为基液时空心球分布情况 Fig.6 Distribution of HGS while applying base liquid as the carrier liquid |
| w/% | 20.0 | 15.0 | 10.0 | 5.0 |
| 入口m球/(kg·s-1) | 5.00 | 4.00 | 2.90 | 1.60 |
| 底部出口m球/(kg·s-1) | 0.63 | 0.77 | 0.55 | 0.00 |
| 上部出口m球/(kg·s-1) | 4.09 | 3.42 | 2.58 | 1.53 |
| 入口m基/(kg·s-1) | 19.90 | 22.70 | 26.00 | 26.32 |
| 底部出口m基/(kg·s-1) | 14.30 | 18.60 | 20.50 | 17.13 |
| 上部出口m基/(kg·s-1) | 2.29 | 3.82 | 5.17 | 9.03 |
| 携带液为基液时η/% | 81.79 | 85.60 | 89.10 | 95.62 |
从表 2可以看出,分离效率随着体积分数增加而降低,质量分数为20.0%时,单级分离效率81.79%,2级分离效率达到90.00%;而质量分数为5.0%时,单级分离效率即可达到95.62%。
4 结论(1) 基于水力旋流器原理,设计了空心球水下注入阀方案,并建立了注入系统整体三维模型。
(2) 采用Fluent软件模拟注入阀内部压力场,采用直径2.5 mm空心球,携带液分别使用海水和基液进行模拟,理论上可以达到多梯度钻井的分离效果。通过分析结果可以看出,分离效率随着空心球的体积分数增加而降低,应根据所需浓度选择合适体积分数注入,从而达到最佳注入效果。
(3) 空心球与基液密度相差较小,同等条件下分离效率较海水携带低,试验中可优先考虑使用海水携带注入。同时为了提高空心球注入浓度,可设计2级旋流器串联来实现空心球的高效分离。
| [1] | 侯芳, 彭军生. 海底泵举升双梯度钻井技术进展[J]. 石油机械, 2013, 41(6): 68–71. |
| [2] | 陈国明, 殷志明, 许亮斌, 等. 深水双梯度钻井技术研究进展[J]. 石油勘探与开发, 2007, 34(2): 246–251. |
| [3] | COHEN J H.Gulf of mexico's first application of riserless mud recovery for top-hole drilling-A case study[C]//Offshore Technology Conference, Houston, Texas, USA, 2010. |
| [4] | ALAWAMI M B.Investigation of the stability of hollow glass spheres in drilling fluids in diverse pH environments and assessment of potential field applications in Saudi Arabia[R].SPE 175737, 2015. |
| [5] | HALKYARD J, ANDERSON M R, MAURER W C.Hollow glass microspheres:An option for dual gradient drilling and deep ocean mining lift[R].OTC 25044, 2014. |
| [6] | 杨树东, 陈国明, 殷志明, 等. 含空心球钻井液分离流场数值模拟[J]. 石油机械, 2007, 35(1): 9–11. |
| [7] | 张鹏飞, 陈国明, 谢丽婉, 等. 基于仿真的海底钻井液举升钻井返回系统[J]. 石油机械, 2011, 39(5): 23–26, 96. |
| [8] | 王卓显. 深水海底泥浆举升钻井系统分析及旋转分隔器设计[D]. 东营: 中国石油大学(华东), 2007. |




