0 引言
随着全球非常规油气资源勘探开发的不断加快,为进一步提高油气勘探开发效益,大斜度井和水平井得到了越来越多的应用。但在钻进中往往因携岩不利,清岩不及时,钻屑在运移过程中在低边堆积而产生了岩屑床,制约着机械钻速和钻井效率的提高,甚至导致憋泵和卡钻等复杂钻井事故。常规的解决方法多为频繁短程起下钻、提高转速和增大排量等,虽有一定效果,但是不能从根本上解决钻进中随时出现的岩屑床[1]。
国内外学者已对此做了大量研究。王智峰[2]对岩屑床形成的原因进行了分析,岩屑颗粒在井筒流动的过程中由于重力的作用,向井眼低边沉降,在大井斜角度处形成岩屑床。杨明合等[3]对大斜度井环空岩屑床厚度进行了评价。魏纳等[4]对水平井岩屑运移进行了可视化研究。刘希圣等[5-6]对岩屑运移的理论做了研究,岩屑在运移过程中受流体拖曳、举升和浮力等作用,在岩屑床表面滚动或举升至上层流体之中,并用试验法预测了岩屑床厚度。刘玉明等[7]系统阐述了大位移井岩屑运移机理,总结了岩屑运移的研究方法,分析了钻井液密度、流变性及排量对岩屑运移的影响。张洪泉等[8]总结了清除岩屑床的方法,包括强化水力参数法[9]、钻柱旋转法[10]以及改进的射流磨钻头设计[11-12]等方法。
改进的射流磨钻头设计仅适用于气体钻井,虽然通过射流磨结构可以大幅度提高携岩效率,但面临着破岩和清岩效率低下及适应面狭窄等问题。笔者在此基础上,通过对风琴管谐振-脉冲生成、射流泵-负压抽汲和高压水射流理论的研究,设计了一种新型钻头——脉冲内磨钻头。该型钻头可产生高速脉冲射流水力辅助高效破岩,具有反向射流负压抽汲钻头底部钻屑以及内磨削结构减小钻屑粒径的特点,实现了高效破岩和清岩,减小了压持效应,提高了机械钻速;同时,该型钻头可应用于常规钻井液钻井,弥补了应用面较为狭窄的缺陷。笔者通过理论计算和实例分析确定了该型钻头的参数取值范围,所得结论可为该钻头的应用和优化提供参考。
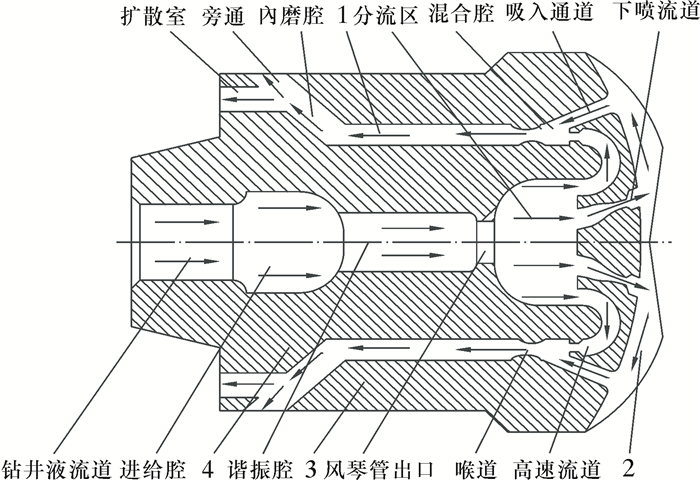
1 脉冲内磨钻头设计方案脉冲内磨钻头由流道、进给腔、谐振腔、出口、分流区、反向高速流道、混合腔、加速管、内磨腔、扩散室、下喷脉冲喷嘴及吸入通道等部分组成,结构如图 1所示。该型钻头结构上没有排屑槽,岩屑经吸入通道和混合腔等循环排出。
|
| 图 1 脉冲内磨钻头结构示意图 Fig.1 Structural schematic of the pulse mill bit 1—加速管;2—刀翼;3—PDC钻头刀翼;4—内磨体。 |
当稳态钻井液流经风琴管[13]出口时,在收缩截面的作用下产生初始压力激动。产生的压力激动经出口被反馈到谐振腔,当压力激动的频率与谐振腔固有频率相匹配时,就会在谐振腔内激发液体共振,产生断续涡流,从而获得脉冲射流;得到的脉冲射流经分流区分别流向下喷流道和反向高速流道,其中下喷的脉冲射流辅助冲击破岩;上返的脉冲射流经反向高速流道喷出,凭借高速特性,在吸入通道的钻头底部形成负压;在负压的作用下,岩屑被抽汲进入混合腔;在混合腔内,岩屑与反向射流形成两相高速紊流;在加速管中,由于钻井液黏滞力的作用,岩屑获得高速度并进入内磨腔;由于颗粒-颗粒和颗粒-内磨体之间的高压作用力及水楔效应的存在,岩屑在内磨腔中被内磨粉碎,速度降底之后,经扩散腔和旁通排出。该钻头的优点主要包括:① 具有风琴管结构。循环钻进的稳态流被转换为脉冲射流,脉冲射流对井底非对称、非均匀的冲击提高了水力辅助破岩的能力。② 具有反向高速流道。产生的高速射流束在吸入通道的钻头底部形成负压,抽汲岩屑,减小压持效应,提高了钻井液的清岩效率。③ 具有内磨削结构。内磨粉碎岩屑,减小颗粒粒径,利于钻井液携岩,清除水平井中的岩屑床。
2 脉冲内磨钻头参数计算模型 2.1 内磨高压作用力钻井液作为高速流体,将能量传递给岩屑,获得高速度的岩屑在内磨腔与内磨体形成撞击,在撞击过程中受到高压作用力被磨削、粉碎。高压作用力为[10]:
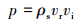
|
(1) |
式中:p为岩屑受到的作用力,Pa;ρs为颗粒密度,kg/m3;vr为内磨末速度,m/s;vi为内磨初速度,m/s。
2.2 最小内磨末速度[14-16]最小内磨末速度是决定高压作用力的关键因素,直接影响着携岩效果。根据bond公式[11],将每907 kg岩屑从初始内磨粒径Di内磨粉碎到内磨终止粒径dt所需要的能量为:

|
(2) |
式中:W为所需的能量,kW·h;Wi为内磨胶结系数,kW·h;dt为内磨终止粒径,μm;Di为内磨初始粒径,μm。
单位岩屑由内磨初始粒径Di被内磨粉碎到内磨终止粒径dt所释放的能量为:
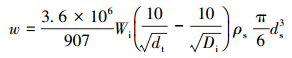
|
(3) |
式中:ds为岩屑内磨粒径,m;ρs为岩屑的密度,kg/m3。
经内磨粉碎,单位岩屑获得的冲击动能为:
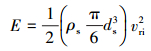
|
(4) |
式中:vri为最小内磨末速度,m/s。
定义内磨能量系数为fi,表征岩屑内磨产生的能量w与冲击动能E之间的能量转化:

|
(5) |
将式(3) 和式(4) 代入(5),计算整理得最小内磨末速度为:

|
(6) |
加速管的长度直接影响最小内磨末速度,为方便最小加速管长度的计算,对岩屑做出如下简化和假设[8]:① 岩屑流入加速管的初速度为0 m/s;② 岩屑为无孔隙、不可压缩的球形颗粒;③ 岩屑以悬浮状态运移。
岩屑经混合腔进入加速管,在加速管中受重力和钻井液黏滞力作用,其大小为:

|
(7) |
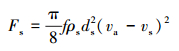
|
(8) |
式中:Gs为岩屑所受重力,N;Fs为岩屑所受黏滞力,N;f为钻井液阻力系数;va为喷嘴出口钻井液流体速度,m/s;vs为岩屑速度,m/s。
岩屑运移满足牛顿第二定律,受力方程为:
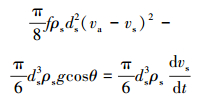
|
(9) |
式中:θ为井斜角,(°)。
阻力系数是颗粒雷诺数Rep的函数[12]。
(1) 若岩屑为小颗粒雷诺数(Rep<0.1) 时,阻力系数为:
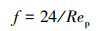
|
(10) |
整理得到l和vs的微分关系式为:
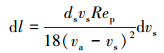
|
(11) |
式中:l为加速度长度,l对时间求导可得vs,即vs=dl/dt。
积分、代入边界条件l=0,vs=0;l=lm,vs=vri,进而可得最小加速管长度lm为:
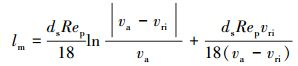
|
(12) |
(2) 若岩屑为中颗粒雷诺数(Rep=25~500) 时,阻力系数为:
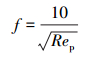
|
(13) |
最小加速管长度lm为:
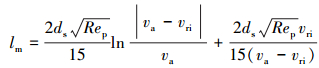
|
(14) |
(3) 若岩屑为大颗粒雷诺数(Rep=500~10 000) 时,阻力系数为:
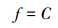
|
(15) |
式中:C为绕流阻力系数,无量纲。
最小加速管长度lm为:
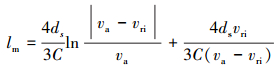
|
(16) |
某区块地层岩性以砂岩和泥岩为主,脉冲内磨钻头直径设计为215.90 mm,钻头内部设置有6个下喷流道,下喷流道内可安装6个常规脉冲喷嘴,喷嘴直径为11.72 mm,机械钻速和旋转速度[17]分别为9.144 m/h和50 r/min;钻进使用的钻井液为水基钻井液,视黏度为0.058 Pa·s,密度为1.08 g/cm3,钻井液排量在考虑水平井临界冲砂排量[18]和水平井临界携岩流量[19-20]的基础上为42.84 L/s;在内磨粉碎过程中,约30%的岩屑能量被转化为冲击动能;经内磨粉碎,砂岩内磨终止粒径[21]为0.90 mm,泥岩为0.50 mm。
基于上述数据,通过运用脉冲内磨钻头参数计算模型,得到砂岩和泥岩的最小内磨末速度和最小加速管长度,结果如表 1所示。
| 岩性 | 内磨终止粒径/mm | 最小内磨末速度/(m·s-1) | 雷诺数 | 最小加速管长度/mm |
| 砂岩 | 0.9 | 64.65 | 796 | 158.45 |
| 泥岩 | 0.5 | 67.08 | 219 | 165.37 |
3 脉冲内磨钻头参数分析
在钻头的具体设计和应用中,有很多因素影响着最小内磨末速度。下面分别讨论内磨能量系数、内磨初始粒径和内磨终止粒径对最小内磨末速度的影响规律。
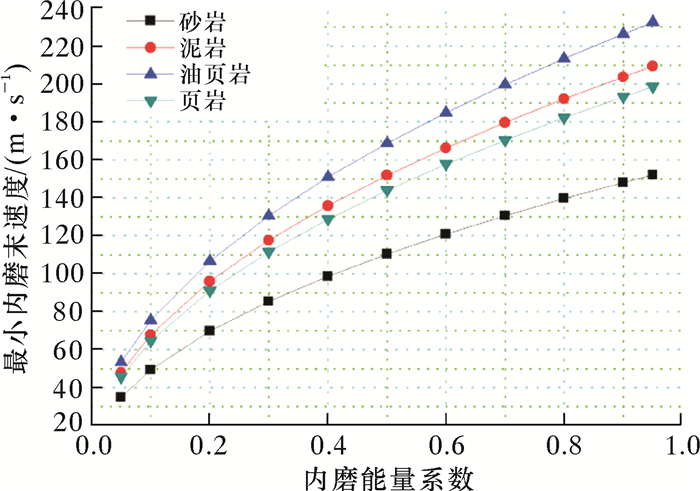
3.1 内磨能量系数的影响在其他参数不变的情况下,内磨能量系数取值范围为0.1~0.9,应用式(2)~式(5),计算得到最小内磨末速度随内磨能量系数变化曲线,如图 2所示。
|
| 图 2 内磨能量系数对最小内磨末速度的影响曲线 Fig.2 Effect of wear energy coefficient on minimum cutting's impact velocity |
由图 2可见,最小内磨末速度随着能量系数的增大而增大,当内磨能量系数较大(fi>0.2) 时,两者近似呈线性相关。因此,在脉冲内磨钻头设计中,必须考虑内磨能量系数的影响。
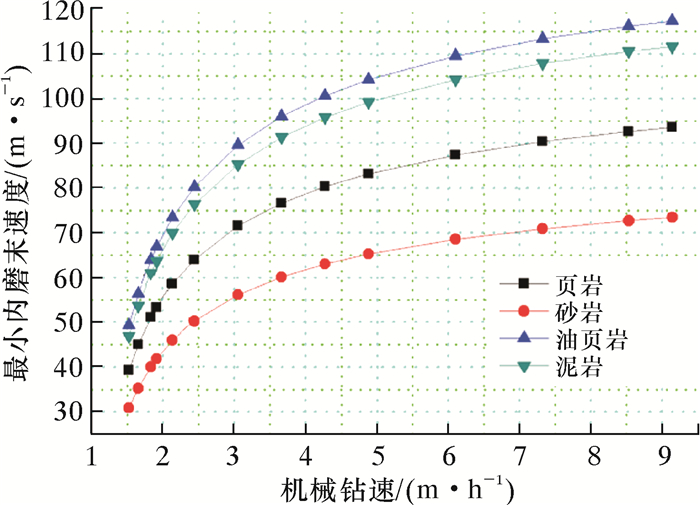
3.2 内磨初始粒径的影响内磨初始粒径由机械钻速决定[8],它直接影响着内磨粉碎岩屑效果。在其他参数不变的情况下,机械钻速取值范围为1.0~9.5 m/h,应用式(2)~式(5),计算得到最小内磨末速度随机械钻速变化的曲线,如图 3所示。
|
| 图 3 机械钻速对最小内磨末速度的影响曲线 Fig.3 Effect of ROP on minimum cutting's impact velocity |
分析图 3可知,最小内磨末速度随机械钻速的增大而增大,当机械钻速较小时(ROP<3.048 m/h),最小内磨末速度变化很快;当机械钻速增大到3.048 m/h时,最小内磨末速度变化较小。因此,在脉冲内磨钻头设计和运用中,必须关注最小内磨初始粒径对最小内磨末速度的影响。
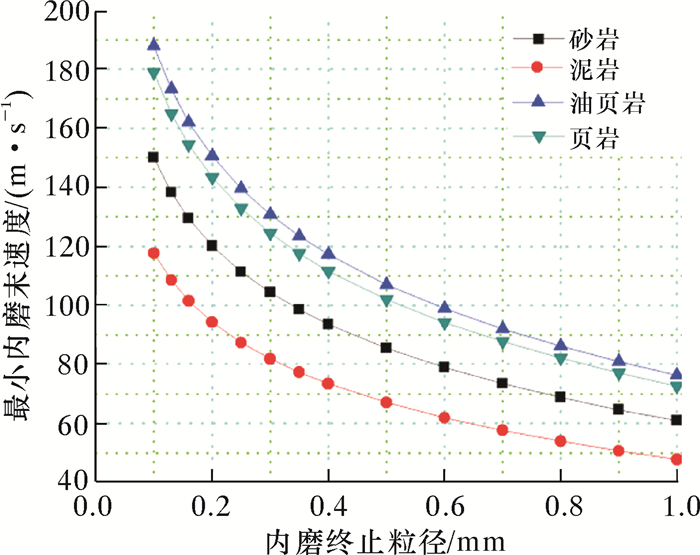
3.3 内磨终止粒径的影响内磨终止粒径直接影响携岩效果。在其他参数不变的条件下,内磨终止粒径取值范围为0.1~1.2 mm,应用式(2)~式(5),计算得到最小内磨末速度随内磨终止粒径变化的曲线,如图 4所示。
|
| 图 4 内磨终止粒径对最小内磨末速度的影响曲线 Fig.4 Effect of final particle size of the cuttings on minimum cutting's impact velocity |
由图 4可见,最小内磨末速度随内磨终止粒径的增大而减小。当内磨终止粒径比较小(dt<0.3 mm)时,最小内磨末速度减小幅度较大;当dt>0.3 mm时,最小内磨末速度变化较小,两者近似呈线性相关。
因此,在脉冲内磨钻头设计中,必须关注最小内磨终止粒径对最小内磨末速度的影响。
4 结论(1) 脉冲内磨钻头是一种新型钻头,通过脉冲射流非对称冲击破岩、反向射流负压抽汲及内磨结构减小钻屑粒径等作用,可望高效破岩和清除水平井岩屑床。
(2) 以钻井液为高速流体,建立了脉冲内磨钻头的参数计算模型,通过算例分析得到砂岩的最小内磨末速度为64.65 m/s,最小加速管长度为158.45 mm,泥岩的最小内磨末速度为67.08 m/s,最小加速管长度为165.37 mm,验证了计算模型的实用性。
(3) 研究结果表明:最小内磨末速度随着能量系数和机械钻速的增大而增大,随内磨终止粒径的增大而减小,特别是当机械钻速小于3.048 m/h、内磨终止粒径小于0.3 mm时,影响比较明显。因此,在脉冲内磨钻头设计与应用中,应关注这些参数的影响。
| [1] | 宋洵成, 王振飞, 徐小龙, 等. 大位移井岩屑床危害及处理措施研究[J]. 石油科技论坛, 2012, 31(2): 40–42. |
| [2] | 王智锋. 复杂结构井岩屑床清除技术[J]. 钻采工艺, 2009, 31(1): 102–104. |
| [3] | 杨明合, 黄彦, 翟应虎, 等. 大斜度井环空岩屑床厚度评价技术及其应用[J]. 天然气工业, 2008, 28(12): 62–64. DOI: 10.3787/j.issn.1000-0976.2008.12.017 |
| [4] | 魏纳, 孟英峰, 李皋, 等. 欠平衡钻水平井岩屑运移可视化实验[J]. 天然气工业, 2014, 34(1): 80–85. |
| [5] | 刘希圣, 郑新权, 丁岗. 大斜度井中岩屑床厚度模式的研究[J]. 石油大学学报(自然科学版), 1991, 15(2): 28–35. |
| [6] | 龙芝辉, 汪志明, 郭晓乐. 斜井和水平井钻井环空流核区及速梯区中岩屑的运移研究[J]. 天然气工业, 2005, 25(6): 62–64. |
| [7] | 刘玉明, 管志川, 呼怀刚. 大位移井岩屑运移研究综述与展望[J]. 科学技术与工程, 2015, 15(28): 88–95. DOI: 10.3969/j.issn.1671-1815.2015.28.016 |
| [8] | 张洪泉, 任中启, 董明健. 大斜度大位移井岩屑床的解决方法[J]. 石油钻探技术, 1999, 27(3): 6–8. |
| [9] | 党克军, 王增年, 简章臣, 等. 水平井岩屑床控制技术浅析[J]. 钻采工艺, 2011, 34(5): 25–27. |
| [10] | 石晓兵. 大位移井中利用钻柱旋转作用清除岩屑床的机理研究[J]. 天然气工业, 2000, 20(2): 51–53. |
| [11] | CHEN X Y, GAO D L, GUO B Y. Optimal design of jet mill bit for jet comminuting cuttings in horizontal gas drilling hard formations[J]. Journal of Natural Gas Science & Engineering, 2015, 28: 587–593. |
| [12] | CHEN X Y, GAO D L, GUO B Y. A method for optimizing jet-mill-bit hydraulics in horizontal drilling[J]. SPE Journal, 2016, 21(2): 101–110. |
| [13] | 陈小元, 王委, 王治国, 等. 一种钻井用PDC钻头: 204532094U[P]. 2015. |
| [14] | LIU Z H, SUN Z N. Wet comminution of raw salt using high-pressure fluid jet technology[J]. Powder Technology, 2005, 160(3): 194–197. DOI: 10.1016/j.powtec.2005.08.027 |
| [15] | BOND F C. Crushing and grinding calculations[J]. Canadian Mining & Metallurgical Bulletin, 1960, 47(507): 466–472. |
| [16] | 樊洪海. 实用钻井流体力学[M]. 北京: 石油工业出版社, 2014. |
| [17] | GUO B, GHALAMBOR A. Gas volume requirements for underbalanced drilling:Deviated holes[M]. Oklahoma: PennWell Corp, 2002. |
| [18] | 刘清友, 汪兴明, 徐涛. 考虑瞬态温度场的水平井水力冲砂临界排量[J]. 西南交通大学学报, 2014, 49(6): 1123–1129. |
| [19] | VIEIRA P, MISKA S, REED T, et al.Minimum air and water flow rates required for effective cuttings transport in high angle and horizontal wells[C]//IADC/SPE Drilling Conference.Canada:Society of Petroleum Engineers, 2002. |
| [20] | CHEN X Y, GAO D L, GUO B Y, et al. A new method for determining the minimum gas injection rate required for hole cleaning in horizontal gas drilling[J]. Journal of Natural Gas Science & Engineering, 2014, 21: 1084–1090. |
| [21] | 易先中, 王利成, 魏慧明, 等. 钻井岩屑粒径分布规律的研究[J]. 石油机械, 2007, 35(12): 1–4. DOI: 10.3969/j.issn.1001-4578.2007.12.001 |




