2. 中国石油化工股份有限公司石油工程技术研究院
2. Sinopec Research Institute of Petroleum Engineering
0 引言
页岩气大规模压裂作业过程中,压裂泵将常压下一定黏度的压裂液转化为高压力、大排量的液体排出,用作挤压油气层和支撑裂缝的介质。因此,压裂泵是整个压裂车的心脏,其安全性和可靠性关系到整体压裂作业的顺利进行[1]。长期服役的压裂泵受到周期性变化的复杂载荷作用,易发生疲劳失效和断裂破坏;压裂过程中一旦出现上述现象,相关单位不得不停产检修和更换部件,因此寻找压裂泵疲劳失效规律以及计算其疲劳寿命具有重要意义[2]。
但压裂施工工况繁复,现场试验耗费人力物力,数值求解过程繁琐,且均存在一定的难度。国内外已有学者运用有限元分析法对压裂泵进行研究[3-4]。例如:针对柱塞和泵头体,在疲劳寿命计算的基础上,开展性能分析、自增强处理和结构优化等技术研究[5-7];针对曲柄连杆机构,通过有限元静力分析和模态分析,获取疲劳寿命和疲劳安全系数,为结构改进提供理论依据[8-11];针对蜗轮蜗杆机构,利用有限元分析软件进行热力学分析并获取应力应变状态[12]。
目前针对页岩气压裂作业特点,压裂泵应力应变随施工工况、载荷和压力如何变化,以及不同压力条件下疲劳失效有何规律,相关研究仍处于空白状态。上述研究工作的缺失将大大增加作业风险,难以保障压裂泵平稳、安全运行。为此,选取柱塞、泵头体、连杆、曲柄、蜗轮和蜗杆等6个主要部件,利用ANSYS软件,通过建立三维模型、设定边界约束条件以及施加工况载荷-压力,进行有限元静力分析;并基于FE-SAFE平台,通过合理提取静力分析结果确定载荷谱进行疲劳寿命计算。最终,揭示了不同压力工况下各部件应力、位移状态及疲劳脆弱点位置;明确了各部件应力、位移及疲劳寿命随压力变化的规律;绘制了各部件应力、位移、疲劳寿命与压力的关系曲线,以及变压力工况下各部件和压裂泵整体的疲劳失效演化图谱。研究结果可为现场压裂安全施工提供技术支撑。
1 疲劳分析理论工程中广泛采用适用于延性金属的修正Brown-Miller疲劳计算方法[10],该算法认为最大疲劳损伤出现在最大剪平面上,且损伤同时为剪平面上剪应变和正应变的函数。设最大剪应变γmax=ε1-ε3,最大正应变εn=(ε1+ε3)/2,单轴平面应变中,ε3=-νε1,则有:
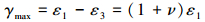
|
(1) |
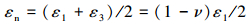
|
(2) |
式中:ν为泊松比;ε1、ε2和ε3分别为第一、第二和第三主应变。
传统应变-寿命方程为:
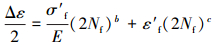
|
(3) |
式中:Δε为应变范围;E为弹性模量;2Nf为以反向计数的疲劳寿命;σ′f为疲劳强度系数;ε′f为疲劳延性系数;b为疲劳强度指数;c为疲劳延性指数。
将式 (3) 左端改写为剪应变和正应变幅值之和,得Brown-Miller应变-寿命方程:
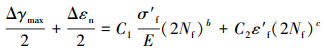
|
(4) |
式中:Δγmax、Δεn分别为剪应变和正应变范围;C1、C2为常系数;右端第1项为弹性应变,C1=1.65;第2项为塑性应变,C2=1.75。
考虑平均应力,利用Morrow平均应力准则修正得应变-寿命公式:
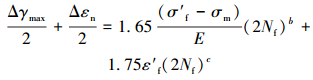
|
(5) |
式中:σm为平均应力。
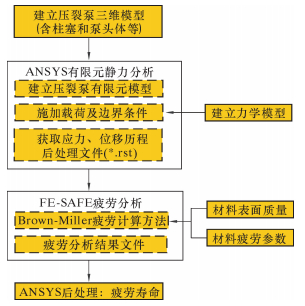
基于上述理论,利用FE-SAFE平台对压裂泵疲劳寿命进行研究,疲劳分析流程如图 1所示。
|
| 图 1 疲劳分析流程 Fig.1 Fatigue analysis process |
2 压裂泵主要部件疲劳失效模拟
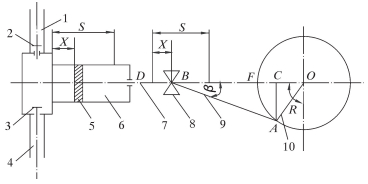
压裂泵通过曲柄连杆机构带动柱塞不断往复运动,改变泵头体内腔的压力,从而实现液体的吸入和排出。其主要承载部件相互作用的基本结构如图 2所示。其中,柱塞受拉压力作用,泵头体内腔存在柱塞压力和油液压力的交叉叠加力,曲柄连杆由动力端提供动力传递拉压力,蜗轮蜗杆转换能量。
|
| 图 2 压裂泵主要承载部件力学模型 Fig.2 Mechanical model of major loading parts of fracturing pump 1—排出管;2—排出阀;3—吸入阀;4—吸入管;5—活塞;6—工作腔;7—活塞杆;8—十字头;9—连杆;10—曲柄。 |
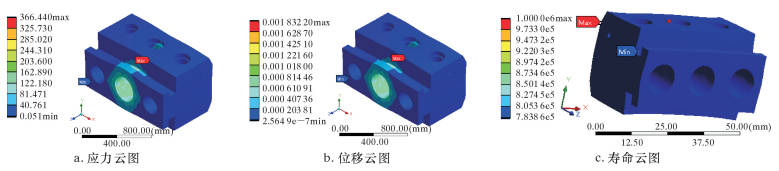
利用Solidworks建立三维模型,相关建模参数、网格划分和边界约束条件如下所述,并将柱塞、泵头体、连杆、曲柄、蜗轮和蜗杆等6个主要部件的三维模型导入ANSYS软件。利用ANSYS软件对柱塞、泵头体、连杆、曲柄、蜗轮和蜗杆等6个主要部件进行应力和位移分析,并基于FE-SAFE平台计算疲劳寿命,模拟结果分别如图 3~图 5所示。限于篇幅,此处仅列出柱塞、泵头体和连杆的模拟结果。

|
| 图 3 柱塞疲劳失效模拟结果 Fig.3 Fatigue failure simulation results of plunger |
|
| 图 4 泵头体疲劳失效模拟结果 Fig.4 Fatigue failure simulation results of pump head |
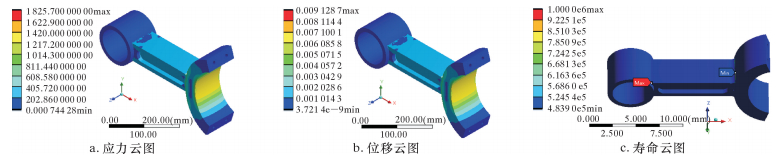
|
| 图 5 连杆疲劳失效模拟结果 Fig.5 Fatigue failure simulation results of connecting rod |
2.1 柱塞
材料40CrNiMoA,弹性模量206 GPa,泊松比0.3,密度7 870 kg/m3。采用Workbench智能网格划分,并对网格进行细化。如柱塞直径95.3 mm,以70 MPa为例,力的计算结果为498 790.25 N。
2.2 泵头体长1 200 mm,宽600 mm,高750 mm,柱塞腔直径220 mm,吸入口直径170 mm,排出口直径120 mm,材料40CrNiMoA,弹性模量206 GPa,泊松比0.3,密度7 870 kg/m3,网格划分选取Solid187单元,属于中间节点的四面体单元,适于生成不规则网格模型。
对称面施加对称约束,泵头体与动力端连接处施加全约束。建模时简化吸入盖总成和排出盖总成处的螺纹切除直径。
2.3 连杆中心长度428 mm,厚度116 mm,小环内径100 mm,小环外径139 mm,大环内径116 mm,大环外径214 mm,材料40CrNiMoA;弹性模量206 GPa,泊松比0.3,密度7 870 kg/m3。连杆结构对称且复杂、接触面较多,采用Workbench网格划分并细化。根据假设的接触面性质,将边界条件确定为:在连杆小端内表面上节点自由度全部约束,连杆大端加载荷。
2.4 曲柄大环直径为112 mm,大环厚度为28 mm,小环直径为28 mm,小环高度为45 mm,材料40CrNiMoA,弹性模量206 GPa,泊松比0.3,密度7 870 kg/m3。采用Workbench四面体划分网格并细化。作业时曲柄主要承受柱塞和连杆周期性变化的惯性力及连杆力,集中于曲柄和偏心轮接触面上。在不影响结构完整性和正确性的前提下,忽略其内部细小油管道,认为整体是实体结构无空腔。
2.5 蜗轮齿顶圆直径400 mm,齿根圆直径386 mm,齿距15 mm,厚度63 mm,材料40CrNiMoA,弹性模量206 GPa,泊松比0.3,密度7 870 kg/m3。蜗轮机构采用三维10节点四面体Solid187单元,接触位置进行网格的局部细化,并对蜗轮输入扭矩、径向约束和轴向约束。
2.6 蜗杆总长580 mm,螺距25 mm,圈数6,螺纹长150 mm,材料40CrNiMoA,弹性模量206 GPa,泊松比0.3,密度7 870 kg/m3。采用十节点四面体单元,接触位置网格细化,输入扭矩、径向和轴向约束。
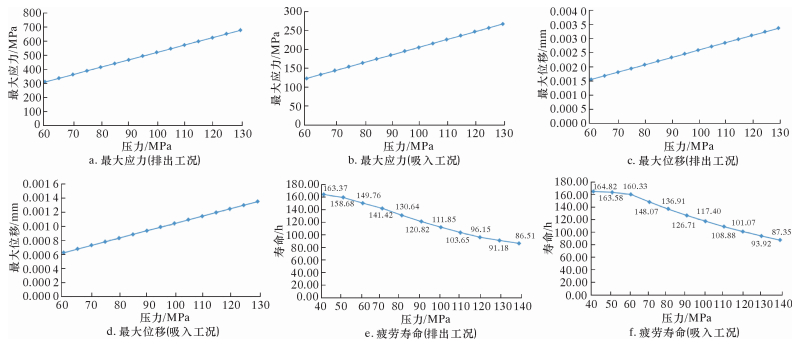
3 压裂泵疲劳失效演化规律研究 3.1 柱塞疲劳失效演化规律 3.1.1 应力和位移状态绘制柱塞的最大应力和最大位移随压力变化的曲线图,如图 6a和图 6b所示。从应力云图可看出,柱塞在作业时,拉杆与本体连接处发生应力集中现象,远离连接处应力分布较均匀,均小于屈服强度836 MPa,满足工况要求。从位移云图可看出,柱塞本体分布较均匀,位移最大发生在拉杆与本体连接处,但小于要求的0.005 mm,位移在允许范围之内,满足使用要求。从曲线图中可看出,柱塞最大应力和最大位移随压力的增加而近似呈线性增加关系,数学表达如式 (6) 和式 (7) 所示。

|
(6) |
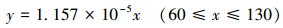
|
(7) |
|
| 图 6 变压力工况下柱塞疲劳失效演化图谱 Fig.6 Fatigue failure evolution graphs of plunger under the changing pressure conditions |
3.1.2 疲劳寿命分析
绘制柱塞的疲劳寿命随压力变化的曲线图,如图 6c所示。
从寿命云图可看出,柱塞疲劳寿命最小值出现在杆身与小头过渡处。例如,压力70 MPa时柱塞 (直径95.3 mm) 疲劳寿命160.85 h,假设一口页岩气井连续作业12段、每段压裂3 h,则柱塞在此工况下服役约4.5口井后需进行检测和维修,以防疲劳破坏导致失效。在此,疲劳寿命定义为一种需检维修的临界值。
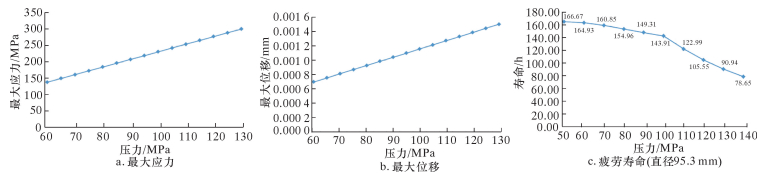
3.2 泵头体疲劳失效演化规律 3.2.1 应力和位移状态绘制泵头体的最大应力和最大位移随压力变化的曲线图,如图 7a~图 7d所示。从应力云图可看出,排出工况时泵头体的柱塞腔和排出腔相贯线处发生应力集中现象,吸入工况时泵头体的排出腔和排出管汇交汇的上部边缘处发生应力集中现象,且应力值由内向外逐渐减小,外壳压力趋于0,均小于屈服强度836 MPa,满足工况要求。
|
| 图 7 变压力工况下泵头体疲劳失效演化图谱 Fig.7 Fatigue failure evolution graphs of pump head under the changing pressure conditions |
从位移云图可看出,泵头体位移最大发生在柱塞腔和排出腔、排出腔和排出管线的相贯处,但小于要求的0.005 mm,应变在允许范围之内,满足使用要求。从曲线图可看出,泵头体最大应力和最大位移随压力的增加而近似呈线性增加关系,数学表达如下:

|
(8) |
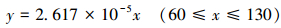
|
(9) |

|
(10) |
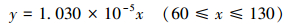
|
(11) |
绘制泵头体的疲劳寿命随压力变化的曲线图,如图 7e和7f所示。
从寿命云图可看出,泵头体疲劳寿命最小值出现在内腔相贯处,这一结果很好地解释了作业时泵头体开裂现象。例如,排出工况且压力70 MPa时泵头体疲劳寿命为141.42 h,假设一口页岩气井连续作业12段、每段压裂3 h,则泵头体在此工况下服役约4口井后需进行检测和维修,以防疲劳破坏导致失效。
3.3 连杆疲劳失效演化规律 3.3.1 应力和位移状态绘制连杆的最大应力和最大位移随压力变化的曲线图,如图 8a和图 8b所示。从应力云图可看出,连杆在作业时,杆身应力分布均匀,杆身与小头过渡处应力最大,但小于屈服强度836 MPa,满足工况要求。从位移云图可看出,连杆杆身分布较均匀,大小头变化不大。位移最大发生在杆身与小头过渡处,但小于要求的0.005 mm,假设加入杆盖变形量将更小,位移在允许范围之内,满足使用要求。从曲线图可看出,连杆最大应力和最大位移随压力的增加而近似呈线性增加关系,数学表达如式 (12) 和式 (13) 所示。

|
(12) |
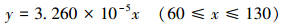
|
(13) |
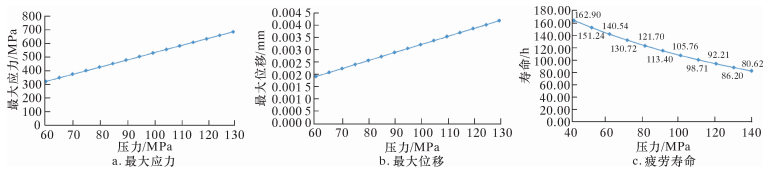
|
| 图 8 变压力工况下连杆疲劳失效演化图谱 Fig.8 Fatigue failure evolution graphs of connecting rod under the changing pressure conditions |
3.3.2 疲劳寿命分析
绘制连杆的疲劳寿命随压力变化的曲线图,如图 8c所示。由图可知,连杆疲劳寿命最小值出现在杆身与小头过渡处。例如,压力70 MPa时连杆疲劳寿命130.72 h,假设一口页岩气井连续作业12段、每段压裂3 h,则连杆在此工况下服役约3.5口井后需进行检测和维修,以防疲劳破坏导致失效。
3.4 曲柄疲劳失效演化规律 3.4.1 应力和位移状态绘制曲柄的最大应力和最大位移随压力变化的曲线图,如图 9a和图 9b所示。从应力云图可看出,曲柄中间部分应力均匀,最大应力位于偏心轮与轴连接圆角处,但小于屈服强度836 MPa,满足工况要求。从位移云图可看出,曲柄位移主要集中于轴中间及偏心轮与轴接触处,但小于要求的0.005 mm,位移在允许范围之内,满足使用要求。
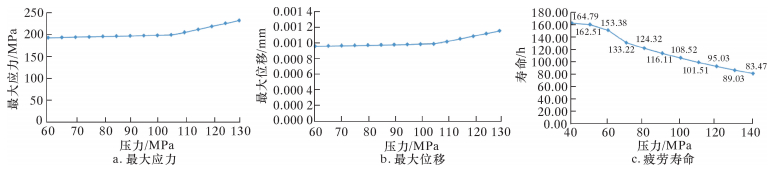
|
| 图 9 变压力工况下曲柄疲劳失效演化图谱 Fig.9 Fatigue failure evolution graphs of crank under the changing pressure conditions |
3.4.2 疲劳寿命分析
绘制曲柄的疲劳寿命随压力变化的曲线图,如图 9c所示。由图可知,曲柄疲劳寿命最小值出现在曲柄销过渡圆根处。例如,压力70 MPa时曲柄疲劳寿命133.22 h,假设一口页岩气井连续作业12段、每段压裂3 h,则曲柄在此工况下服役约3.5口井后需进行检测和维修,以防疲劳破坏导致失效。
3.5 蜗轮疲劳失效演化规律 3.5.1 应力和位移状态绘制蜗轮的最大应力和最大位移随压力变化的曲线图,如图 10a和图 10b所示。从应力云图可看出,蜗轮中心孔处发生应力集中现象,且应力由中心向边缘逐渐减小,均小于屈服强度836 MPa,满足工况要求。从位移云图可看出,位移最大发生在蜗轮中心孔处,但小于要求的0.005 mm,位移在允许范围之内,满足使用要求。从曲线图可看出,蜗轮最大应力和最大位移随压力的增加而近似呈线性增加关系,数学表达如式 (14) 和式 (15) 所示。
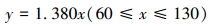
|
(14) |
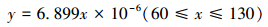
|
(15) |
绘制蜗轮的疲劳寿命随压力变化的曲线图,如图 10c所示。从寿命云图可看出,蜗轮疲劳寿命最小值出现在中心孔处。例如,压力70 MPa时蜗轮疲劳寿命150.64 h,假设一口页岩气井连续作业12段、每段压裂3 h,则蜗轮在此工况下服役约4口井后需进行检测和维修,以防疲劳破坏导致失效。
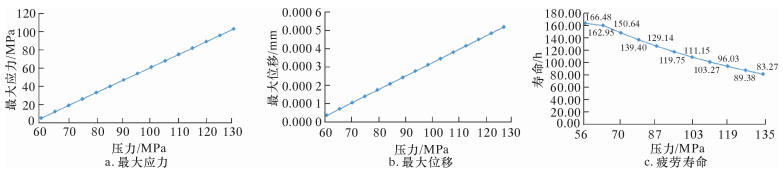
|
| 图 10 变压力工况下蜗轮疲劳失效演化图谱 Fig.10 Fatigue failure evolution graphs of worm gear under the changing pressure conditions |
3.6 蜗杆疲劳失效演化规律 3.6.1 应力和位移状态
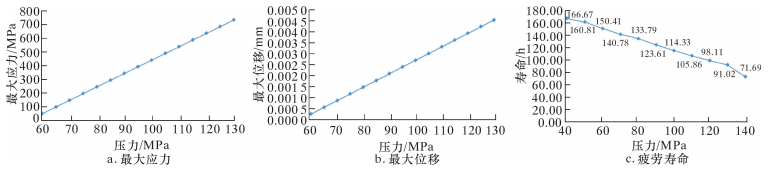
绘制蜗杆的最大应力和最大位移随压力变化的曲线图,如图 11a和图 11b所示。从应力云图可看出,蜗杆销孔处应力较大且由销孔向两端逐渐减小,均小于屈服强度836 MPa,满足工况要求。从位移云图可看出,蜗杆位移最大值出现在销孔处,但小于要求的0.005 mm,位移在允许范围之内,满足使用要求。从曲线图可看出,蜗杆最大应力和最大位移随压力的增加而近似呈线性增加关系,数学表达如式 (16) 和式 (17) 所示。

|
(16) |
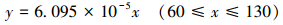
|
(17) |
|
| 图 11 变压力工况下蜗杆疲劳失效演化图谱 Fig.11 Fatigue failure evolution graphs of worm under the changing pressure conditions |
3.6.2 疲劳寿命分析
绘制蜗杆的疲劳寿命随压力变化的曲线图,如图 11c所示。
从寿命云图可看出,蜗杆疲劳寿命最小值出现在销孔处。例如,压力70 MPa时蜗杆疲劳寿命140.78 h,假设一口页岩气井连续作业12段、每段压裂3 h,则蜗杆在此工况下服役约4口井后需进行检测和维修,以防疲劳破坏导致失效。
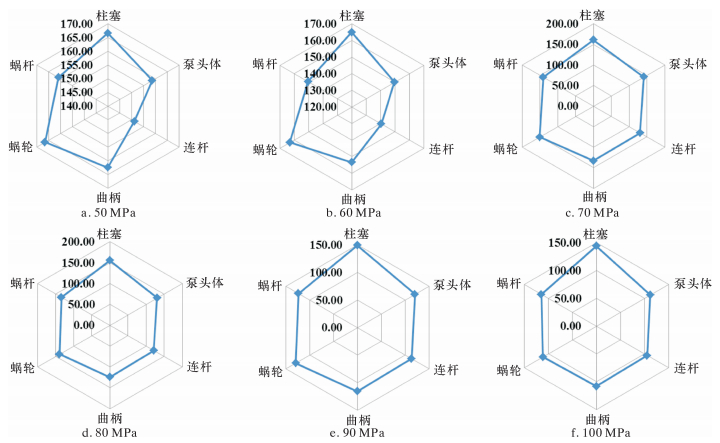
3.7 压裂泵疲劳脆弱点转移规律根据上述各部件疲劳失效模拟结果,选取压力50~100 MPa,绘制压裂泵整体疲劳脆弱点的转移图谱,如图 12所示。由图可以看出,压力50~60 MPa时连杆和泵头体疲劳寿命最短,压力70~100 MPa时连杆和曲柄疲劳寿命最短,易产生疲劳失效,属于压裂泵断裂破坏的主要薄弱点;据此针对各压力工况加强现场监测管理 (图谱中柱塞直径选取95.3 mm,泵头体选取排出工况)。
|
| 图 12 压裂泵疲劳脆弱点转移图谱 Fig.12 Transfer graphs of fracturing pump's fatigue weak points |
4 结论
针对页岩气大规模作业,开展了压裂泵主要部件 (含柱塞、泵头体、连杆、曲柄、蜗轮和蜗杆等) 的有限元静力分析和疲劳寿命计算研究,可得出如下结论:
(1) 揭示了不同压力条件下压裂泵各部件应力、位移状态及脆弱点位置。分别阐述了各部件出现应力集中和最大变形现象的位置,如柱塞的拉杆与本体连接处发生应力集中现象、且出现较大变形,但在最大许用范围内,各部件均满足工况要求。
(2) 明确了压裂泵各部件应力、位移和疲劳寿命随压力变化的规律与关系。其中,柱塞、泵头体、连杆蜗轮和蜗杆的最大应力、最大位移随压力的增加而近似呈线性增加关系。
(3) 得出了变压力工况下压裂泵的疲劳脆弱点转移规律。当压力从50~60 MPa变为70~100 MPa时,疲劳脆弱点从连杆、泵头体转移到连杆、曲柄。
(4) 求解了不同压力条件下压裂泵各部件的疲劳寿命。以压力70 MPa为例,柱塞、泵头体、连杆、曲柄、蜗轮和蜗杆的疲劳寿命分别为160.85、141.42、130.72、133.22、150.64和140.78 h,即分别服役约4.5、4.0、3.5、3.5、4.0和4.0口井后需进行检测和维修。
| [1] | WANG G R, CHEN L Y, ZHAO M, et al. The research on failure analysis of fluid cylinder and fatigue life prediction[J]. Engineering Failure Analysis, 2014, 40: 48–57. DOI: 10.1016/j.engfailanal.2014.01.007 |
| [2] | HE X, LIU Q Y, ZHAO M, et al. Fatigue prediction for pump end of high pressure fracturing pump[J]. Advanced Materials Research, 2011, 337: 81–86. DOI: 10.4028/www.scientific.net/AMR.337 |
| [3] | 李文亮. 大功率压裂泵动力端的设计与分析[D]. 大连: 大连理工大学, 2014. |
| [4] | 杜晓旭. 高压压裂泵液力端设计与研究[D]. 大连: 大连理工大学, 2014. |
| [5] | 闫志琴. 压裂泵柱塞优化设计研究[J]. 制造业自动化, 2015(16): 54–58. |
| [6] | 莫丽, 刘清友, 黄云, 等. 压裂泵阀箱强度及寿命分析[J]. 石油机械, 2009, 37(2): 29–31. |
| [7] | 张磊, 梁政, 姜华. 140 MPa压裂泵液缸强度及寿命预测分析[J]. 石油矿场机械, 2011, 40(4): 26–28. |
| [8] | 李向龙, 芮执元, 雷春丽, 等. 压裂泵连杆疲劳强度分析[J]. 机械制造, 2014, 52(12): 60–62. DOI: 10.3969/j.issn.1000-4998.2014.12.019 |
| [9] | 李向龙, 芮执元, 雷春丽, 等. 压裂泵连杆动态特性分析[J]. 机械制造, 2015, 53(1): 23–25. |
| [10] | 高媛, 单东升, 李文亮, 等. 140 MPa压裂泵曲轴疲劳寿命有限元分析[J]. 石油矿场机械, 2015, 44(2): 68–71. |
| [11] | 叶晓琰, 张军辉, 蒋小平, 等. 基于ANSYS-FATIGUE的曲轴疲劳寿命计算[J]. 流体机械, 2011, 39(4): 44–47. |
| [12] | 陈海峰, 王欢, 翟培培. 基于有限元法的蜗轮蜗杆热力学分析[J]. 机械传动, 2014(10): 170–172. |




