0 引言
超高压管道和容器工作压力大多在100 MPa以上,正常工况下承受着开、停工循环超高内压作用与酸化介质等因素的作用,内壁容易造成应力集中和裂纹扩展,严重影响着超高压管道的疲劳寿命。文献[1]表明:自增强技术可提高超高压容器弹性承载能力,延长其疲劳寿命。
超高压管道的自增强处理是投入正常使用前在其内部施加远高于工作压力的压力,使其内壁材料发生塑性变形,而外层材料保持弹性状态,泄压后在管道内形成有用的残余应力,能很好地改善管道的静强度和疲劳强度[2]。
目前对超高压管道自增强处理的研究,文献[3-4]得出了某型号超高压管道的自增强压力值一般在400~450 MPa之间。因此,如何保证管道自增强处理过程中在如此高的压力作用下不发生泄漏是本技术的关键。笔者针对超高压管道自增强处理时密封技术中的难点,对端面处提出了组合锥环硬密封与环孔轴向组合挡圈相配合的自紧密封结构形式,对组合锥环密封的接触面进行了有限元分析,根据锥角选择原则[5]得到了2锥环密封的最佳锥角,对组合挡圈的厚度及结构进行了设计计算和分析,并得出了最佳的挡圈厚度及结构形式。
1 超高压管道自增强处理密封方案 1.1 密封要求对于自增强处理的密封需要解决2个方面问题:①如何抵消超高压引起的反向作用力,同时保证装置在超高压力作用下满足强度要求;②如何保证超高压作用下的良好的密封性要求。目前对第1类问题的解决方案是结合自增强处理的加压方式,采用外置式装置来抵消超高压力的作用。由于非金属密封只适用于常规的中低高压密封,对于超高压力装置无法起到密封作用,所以采用金属密封。一般对金属接触面需要进行预紧,即实现自紧密封,使得密封面达到较高的接触压力,保证结构的密封性,其中自紧作用多以锥形结构实现[6]。
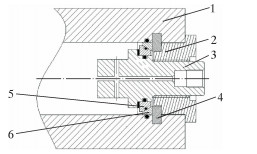
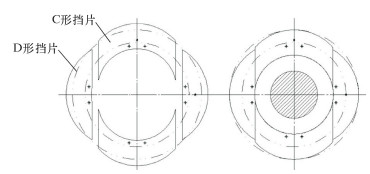
1.2 密封结构绝大多数超高压管道和容器为单层厚壁筒形结构,结合其结构形式、自增强处理时的超高压工艺和各种密封形式的适用范围,提出了如下密封形式:非加压端的密封因不涉及开孔加压等操作,采用平垫密封、双锥密封或其他多种形式的密封结构[7];加压端采用如图 1所示的密封结构。由里向外依次装有加压装置、密封平垫片、外锥面密封环、内锥面密封环、环孔轴向挡圈组合和外锥面螺母。环孔轴向挡圈组合由2片环孔轴向C形挡片和2片环孔轴向D形挡片组成,结构如图 2所示。从超高压管道与组合密封结构形成的环空中装入。超高液压通过加压装置通入,其右端通过外锥面密封和内锥面密封环径向支撑在超高压管道上。自增强处理完后可将管道与挡圈装配的部分切除,不影响管道的使用和应力的分布。
|
| 图 1 超高压管道自增强处理加压端密封结构示意图 Fig.1 Structural schematic of the sealing structureof the pressurized end for ultra-high pressurepipeline self-reinforced process 1—超高压管道;2—外锥面螺母;3—加压装置;4—环孔轴向挡圈组合;5—外锥面密封环;6—内锥面密封环。 |
|
| 图 2 环孔轴向挡圈组合结构示意图 Fig.2 Structural schematic of the composite annular axial ring |
2 加压端组合锥环密封分析
在整个超高压管道容器自增强处理密封中,由于采用的自增强加压方式为液压胀压法,所以加压端的密封至关重要。首先分析组合锥环的密封可靠性。组合锥环的密封效果主要受密封锥角的影响。
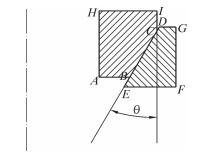
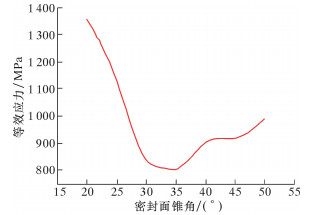
内、外锥环密封二维模型示意图如图 3所示。图中,在BC与DE之间建立接触对,摩擦因数设为0.2,对模型施加适当的边界条件并在HI上施加固定载荷,选用有限元软件对此例进行分析计算。锥面密封环所采用的材料屈服强度σs=880 MPa,抗拉强度σb=1 020 MPa。取压力p为定值 (p=450 MPa),文献[5]表明,锥面密封的锥角在30°附近为宜,故笔者将锥角值的变化范围设定在20°≤θ≤50°,对这些工况下的锥密封模型进行分析,分析结果如图 4所示。
|
| 图 3 内、外锥环密封二维模型示意图 Fig.3 Two-dimensional model of inner and outer taper ring seal |
|
| 图 4 不同锥角接触面处等效应力峰值曲线 Fig.4 Equivalent stress peak at contact surface withdifferent taper angle |
从图 4可以看出:随着锥角的增大,450 MPa作用下接触面上最大等效应力呈先减小后增大的趋势,35°锥角时出现最小值。因此,结合材料的结构强度,当密封面锥角θ=30°或θ=35°时,在最大自增强压力作用下,接触面上的等效应力峰值均比较小,可以使锥密封获得较高的结构强度。
考虑到材料的屈服极限,当密封锥角为30°≤θ≤50°时,锥角对材料结构强度的影响不明显,这个锥角范围内的接触应力曲线见图 5。
|
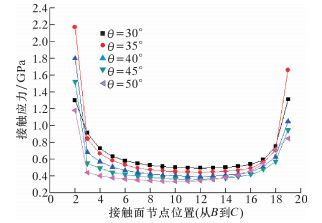
| 图 5 不同锥角接触面处接触应力分布曲线 Fig.5 Distribution of contact stress at contact surface withdifferent taper angle |
从图 5可知:密封面的接触应力沿着接触面 (从B到C) 呈现出先减小后增大的趋势;并且接触面处接触应力在越靠近锥面两端处应力集中越明显,在远离锥面两端处,接触应力的大小变化不明显;但随着锥角的减小,远离锥面两端面处的接触应力逐渐变大。锥面的接触应力应满足不等式qMF≤q,其中q为锥角的接触应力,qMF为密封面必需比压,其值根据阀门技术手册[8]中的密封比压公式确定,即:
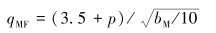
|
(1) |
式中:bM为接触面宽度, mm。
由式 (1) 计算得出各锥角时的必需密封比压如表 1所示。
| 锥角/(°) | 接触面宽度/mm | 必需密封比压/MPa |
| 30 | 8.43 | 493.9 |
| 35 | 8.91 | 480.4 |
| 40 | 9.53 | 464.5 |
| 45 | 10.32 | 446.4 |
| 50 | 11.36 | 425.5 |
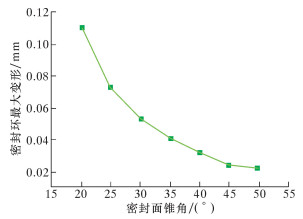
分别对比图 5与表 1中各锥角对应的接触应力和必需密封比压的大小可以得出:当密封面锥角θ变大时,密封面远离锥面两端面处的接触应力逐渐减小,甚至小于接触面必需密封比压。综合对比之后得出,密封面锥角θ=30°时密封效果最佳。有限元分析得到不同锥角密封环最大变形如图 6所示。由图可知:密封面锥角θ越大,密封环最大变形量越小。故在超高压压力作用下,密封面锥角越大,越有助于密封环刚度的提高。
|
| 图 6 不同密封面锥角密封环最大变形图 Fig.6 The maximum deformation of sealing surface withdifferent angle |
综合以上分析可知,在内、外锥面大径和小径一定的前提下,密封面锥角θ=30°为最佳锥面密封结构。这种结构在超高自增强压力作用下既能确保密封的可靠性,又能保证结构强度和刚度。
3 环孔轴向挡圈厚度设计分析环孔轴向挡圈组合主要起阻止锥环移动的作用。挡圈组合类似孔用弹性挡圈的功能,其安全性能主要受挡圈厚度的影响。由于高压管道结构为通孔形状,又作为加压端密封,所以在端面位置处设置了4个挡圈用于消除高压流体作用力。为防止整个环孔轴向挡圈组合结构受高压作用而喷射,影响密封的安全性和可靠性,其关键因素是设计出合理的挡圈厚度和其与管道接触的结构形式。
3.1 理论计算由图 1可以看出,4块挡圈并非直接与高压流体接触,而是通过内、外锥面密封环传递。基于安全性能考虑,在分析计算过程将高压流体直接作用于伸出管道位置处的环形挡圈,以实际最大自增强压力设计,其在挡圈横截面产生的切应力为:
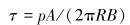
|
(2) |
式中:A为接触压力的作用面积;R为挡圈外径;B为挡圈厚度。
由相关设计资料可查得挡圈材料的许用切应力为[τ],根据强度校核要求可得:
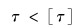
|
(3) |
结合式 (2) 和式 (3) 可得出满足强度要求的挡圈厚度,在设计挡圈时应遵循这一要求。
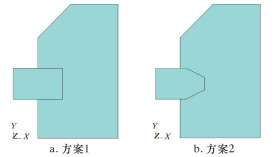
3.2 结构形式分析针对挡圈厚度的设计要求,以厚度作为设计初始条件,对组合挡圈与管壁接触处的结构提出如图 7所示的2种方案。采用有限元方法计算分析,提取2种方案在自增强压力为450 MPa作用下的应力云图,结果分别如图 8和图 9所示。
|
| 图 7 挡圈沿厚度方向结构示意图 Fig.7 Structural schematic of the retaining ring alongthe thickness direction |
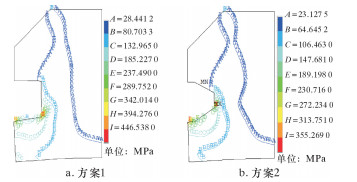
|
| 图 8 高压管道等效应力云图 Fig.8 Equivalent stress distribution of the high pressure pipeline |
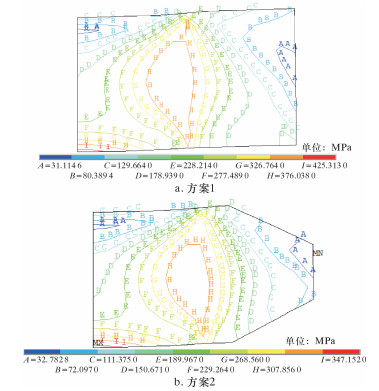
|
| 图 9 挡圈的等效应力云图 Fig.9 Equivalent stress distribution of the retaining ring |
比较图 8与图 9可得:在相同挡圈厚度与工作压力下,方案2中管道与挡圈配合处管壁所产生的最大等效应力值较方案1小,减少幅值达19.56%,挡圈承受的等效应力减少幅值达到18.37%。这说明采用方案2对挡圈应力分布有明显的改善,提高了挡圈强度,保证了结构的可靠性,因此密封装置中挡圈的结构采用方案2进行设计。
4 结论(1) 结合超高压管道与容器的结构和自增强密封技术特点,针对超高压管道自增强处理密封中加压端处提出了组合锥环硬密封和环孔轴向组合挡圈配合的密封结构。
(2) 针对大、小径一定的内、外锥环,通过接触弹塑性有限元分析,得出了组合密封环在不同密封面锥角下,密封面的接触应力和等效应力峰值变化规律,并结合密封材料的结构强度和密封比压,得出内、外锥环的最佳密封面锥角为30°。
(4) 通过理论计算和有限元分析得出了加压端处密封关键件--环孔轴向组合挡圈的厚度及挡圈沿厚度方向满足密封可靠性的结构。
| [1] | 张于贤, 王红, 肖吉军. 基于自增强原理的超高压缸的设计研究[J]. 液压与气动, 2008, 15(11): 64–66. |
| [2] | 周后俊. 压裂泵泵头体自增强技术研究[D]. 荆州: 长江大学, 2009. |
| [3] | 张玲艳, 邱水才, 卢齐英. 基于ANSYS自增强高压管道的承载能力研究[J]. 化工自动化及仪表, 2012(12): 1609–1611. |
| [4] | 张乐廷, 张国民, 汲寿广. 超高压管道 (容器) 应力检测方法[J]. 化工机械, 2004, 31(4): 227–229. |
| [5] | 李宁, 李友荣, 周思柱, 等. 泵头体自增强超高压密封技术研究[J]. 科学技术与工程, 2015, 15(9): 85–89. |
| [6] | 乔培平. 超高压液压密封方法探讨与应用[J]. 液压与气动, 2014, 34(9): 55–57. |
| [7] | 费国标, 刘正林, 海鹏洲, 等. 超高压密封件有限元分析研究[J]. 武汉理工大学学报 (交通科学与工程版), 2006, 30(6): 1055–1057. |
| [8] | 杨源泉. 阀门设计手册[M]. 北京: 机械工业出版社, 2000: 18-20. |




