0 引言
由于建设期技术水平限制和现场焊接施工质量控制等因素,环焊缝及环焊缝缺陷已成为管道结构的薄弱环节,缺陷的不稳定最终会导致环焊缝开裂。管道环焊缝在施工和运行过程中可能会承受较大的轴向应变,例如管道遭遇地震、滑坡、冻土冻融交替、矿区采空深陷及海管敷设等工况[1]。现行的管道设计标准大多遵循传统的基于应力的设计准则,当管材出现屈服和应变强化时,基于应力的设计准则便不再适用[2]。笔者建立了内压作用下三维管道环焊缝缺陷仿真模型,采用基于应变的设计方法对其承载能力进行了分析,探讨了其影响参数的变化规律,以期对管道环焊缝缺陷完整性评价提供理论指导。
1 管道设计准则 1.1 基于应力设计准则基于应力的设计准则以管材的应力极限值作为失效判据,规定管材的应力不超过许用应力,即:

|
(1) |
式中:σ为管材应力;[σ]为管材许用应力;σs为管材最小屈服强度;k为基于应力的设计系数。
《输油管道工程设计规范》(GB 50253-2014) 和《输气管道工程设计规范》(GB 50251-2015) 规定:埋地直管段的轴向应力与环向应力组合的当量应力应小于钢管标准规定的最小屈服强度的90%[3-4],即:
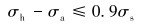
|
(2) |
式中:σh为管段轴向应力,σa为管段环向应力。
基于应力的设计实际上是有一定安全系数的弹性设计,适用于一般地段管道在内压和温差等以力为度量的载荷作用下的强度设计[5]。
1.2 基于应变设计准则基于应变设计准则以管材的应变极限值作为失效判据,即:
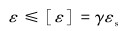
|
(3) |
式中,ε为管材应变;[ε]为管材许用应变;εs为管材极限应变;γ为基于应变的设计系数。
CSA和DNV等标准均采用极限状态设计方法,根据管道的失效模式对其进行基于应变的设计[6]。轴向拉伸载荷作用下管道的失效形式包括脆性断裂、塑性坍塌及延性撕裂等。CSA Z662.1-2011标准[7]中规定,拉伸断裂失效模式下的管道轴向拉应变应满足:
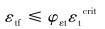
|
(4) |
式中:εtf为管道轴向或环向拉应变;εtcrit为管壁或焊件拉应变极限;φεt为拉应变抗性系数,取0.7。
对于表面开口缺陷有:
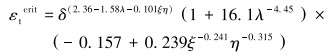
|
(5) |
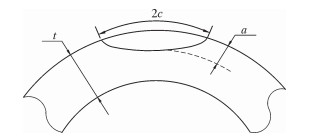
式中:δ为表观CTOD韧度,mm;λ为屈服极限与强度极限的比值;ξ为缺陷长度与管道壁厚的比值,ξ=2c/t;η为缺陷深度与管道壁厚的比值,对于表面开口缺陷η=a/t;t为管道壁厚,mm。
对于公式 (5),CSA Z662.1-2011标准中给出了明确的适用范围:0.7≤δ≤0.9,0.1≤λ≤0.3,1≤ξ≤10,η≤0.5,D/t>32。
表面开口缺陷尺寸示意图见图 1。
|
| 图 1 表面开口缺陷尺寸示意图 Fig.1 Schematic diagram of the dimension of thesurface breaking defects |
2 数值模拟计算 2.1 基本假设
(1) 焊材与母材具有相同的拉伸性能,焊接强度不存在过匹配或欠匹配的情况。
(2) 焊缝盖帽高度可忽略不计,假设焊缝与母材齐平;焊缝盖帽增大了焊缝处壁厚,增强了焊缝承载能力,但由于施工技术限制,管道焊缝盖帽高度可能随位置不同而不同,忽略盖帽高度能够获得偏保守的计算结果[1]。
(3) 已经假设焊材与母材具有相同的拉伸性能,因此忽略焊缝坡口形状的影响。
2.2 材料本构管材选用X65管线钢,其本构采用Ramberg-Osgood修正模型。该模型能够较好地模拟管材实际的拉伸本构关系,其表达式为[8]:
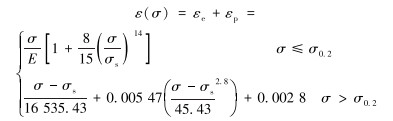
|
(6) |
式中:ε(σ) 为管材应变;εe为弹性应变;εp为塑性应变;E为管材弹性模量,取207 GPa。
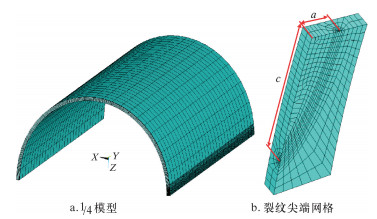
2.3 有限元模型管道单元选择SOLID95,为3D20节点结构六面体实体单元,具有塑性、蠕变、膨胀、应力刚化、大变形和大应变等特性;由于采用协调的位移函数,SOLID95单元可以很好地适应曲线边界。根据基本假设及问题的对称性,建立含环向裂纹缺陷的
|
| 图 2 含裂纹缺陷管道有限元模型 Fig.2 Finite element model of pipe with crack |
2.4 应用实例
分别对不同韧性参数、管道及缺陷尺寸进行了研究,模拟计算得出各变化参数下管道的拉应变极限和失效压力,结果如表 1所示。
| 表观CTOD 韧度/mm |
管径/ mm |
壁厚/ mm |
长厚 比 |
深厚 比 |
拉应变极 限/% |
失效压 力/MPa |
| 0.10 | 610 | 8 | 6 | 0.5 | 0.24 | 8.76 |
| 0.15 | 610 | 8 | 6 | 0.5 | 0.32 | 10.57 |
| 0.20 | 610 | 8 | 6 | 0.5 | 0.40 | 11.31 |
| 0.25 | 610 | 8 | 6 | 0.5 | 0.47 | 11.85 |
| 0.30 | 610 | 8 | 6 | 0.5 | 0.54 | 12.18 |
| 0.20 | 457 | 8 | 6 | 0.5 | 0.40 | 15.35 |
| 0.20 | 508 | 8 | 6 | 0.5 | 0.40 | 13.74 |
| 0.20 | 660 | 8 | 6 | 0.5 | 0.40 | 10.55 |
| 0.20 | 711 | 8 | 6 | 0.5 | 0.40 | 9.77 |
| 0.20 | 610 | 6 | 6 | 0.5 | 0.40 | 8.55 |
| 0.20 | 610 | 7 | 6 | 0.5 | 0.40 | 9.96 |
| 0.20 | 610 | 9 | 6 | 0.5 | 0.40 | 12.83 |
| 0.20 | 610 | 10 | 6 | 0.5 | 0.40 | 14.34 |
| 0.20 | 610 | 8 | 2 | 0.5 | 0.76 | 13.84 |
| 0.20 | 610 | 8 | 4 | 0.5 | 0.53 | 13.65 |
| 0.20 | 610 | 8 | 8 | 0.5 | 0.30 | 9.09 |
| 0.20 | 610 | 8 | 10 | 0.5 | 0.21 | 5.98 |
| 0.20 | 610 | 8 | 6 | 0.1 | 1.83 | 16.08 |
| 0.20 | 610 | 8 | 6 | 0.2 | 1.30 | 14.99 |
| 0.20 | 610 | 8 | 6 | 0.3 | 1.04 | 14.33 |
| 0.20 | 610 | 8 | 6 | 0.4 | 0.88 | 14.03 |
3 计算结果分析 3.1 表观CTOD韧度的影响
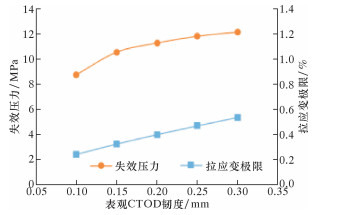
CTOD值的大小反映了材料抗开裂能力的高低,CTOD值越大,表示裂纹尖端处材料的抗开裂性能越好,即韧性越好;反之,韧性越差。图 3为表观CTOD韧度对失效压力的影响曲线。从图可以看出:管道拉应变极限随表观CTOD韧度值的增大近似呈线性增加,印证了材料韧性越好,抗开裂性能越好;管道失效压力亦随表观CTOD韧度的增大而增加,但增幅逐渐递减,说明在拉伸载荷作用下,材料韧性越好,抗变形能力越强,较相对脆性材料,塑性材料在断裂失效前会有较长的塑性变形阶段。因此,管道设计施工中焊材与管材的强度及韧性匹配对管道承载能力有着重要影响。
|
| 图 3 表观CTOD韧度对失效压力的影响曲线 Fig.3 The effect of the apparent CTOD toughnesson failure pressure |
3.2 管径的影响
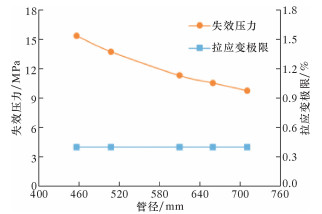
由式 (5) 可知,拉应变极限与管径无关,随着管径的变化而保持不变。图 4为管径对失效压力的影响曲线。由图可知,当管径逐渐增大,径厚比也逐渐增大,管道失效压力逐渐减小,减幅呈递减趋势。由此递推,当管径无限增大,管壁可简化为薄膜,管道失效压力趋于恒定值。
|
| 图 4 管径对失效压力的影响曲线 Fig.4 The effect of pipe diameter on failure pressure |
3.3 壁厚的影响
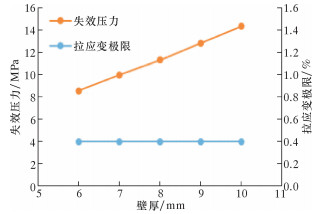
由式 (5) 可知,拉应变极限与缺陷长厚比及深厚比相关,因此在其他参数保持不变的情况下,拉应变极限不随壁厚变化而改变。图 5为壁厚对失效压力的影响曲线。从图可以看出,当壁厚增大时,缺陷环向长度及深度按比例增加,管道失效压力亦近似呈线性递增。
|
| 图 5 壁厚对失效压力的影响曲线 Fig.5 The effect of wall thickness on failure pressure |
3.4 缺陷长度的影响
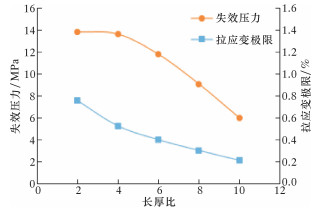
图 6为缺陷长度对失效压力的影响曲线。由图可见,随着缺陷长度的增大,拉应变极限与管道失效压力逐渐减小。拉应变极限减幅逐渐递减,管道失效压力变化曲线存在明显拐点,在长厚比小于4时减幅较小;当长厚比大于4后,失效压力变化曲线递减越来越快。这表明环向裂纹缺陷达到一定长度后,管道承载能力衰减更为明显,因此应严格控制焊接施工质量,避免裂纹尤其是长裂纹的出现。
|
| 图 6 缺陷长度对失效压力的影响曲线 Fig.6 The effect of defect length on failure pressure |
3.5 缺陷深度的影响
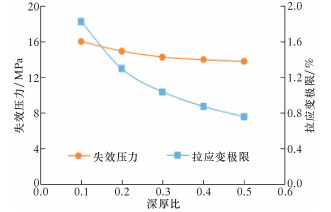
图 7为缺陷深度对失效压力的影响曲线。由图可以看出,拉应变极限与管道失效压力均随着缺陷深度的增加而递减,减幅均呈递减趋势,且管道失效压力变化幅度较小。在研究缺陷深度影响的实例中缺陷长厚比取值为2,从而印证了图 6中长厚比较小时失效压力的变化规律。拉应变极限随着缺陷深度的增加递减幅度较大,对比图 6与图 7可知,管道承载力对缺陷深度的变化更为敏感。
|
| 图 7 缺陷深度对失效压力的影响曲线 Fig.7 The effect ofdefect depth on failure Pressure |
4 结论
(1) 有限元方法能够有效模拟内压下表面裂纹缺陷管道的失效行为,在缺乏宽板拉伸和全尺寸爆破等试验数据时,有限元模拟方法可以提供技术参考。
(2) 材料韧性越好,裂纹尖端抗开裂性能越好,在管道设计施工中应合理选择焊材与管材的强度及韧性匹配。
(3) 相对于管道尺寸,裂纹缺陷尺寸对管道承载能力的影响更大,尤其是缺陷深度。另外,当裂纹环向长度小到一定程度,管道失效压力变化很小。应严格控制焊接施工质量,并根据无损检测结果确定焊缝合格与否。所得结论可为管道环焊缝缺陷完整性评价提供理论指导。
| [1] | WANG Y Y, CHENG W T, MCLAMB M, et al.Tensile strain limits of girth welds with surface-breaking defects-Part 1:An analytical framework[C]//Proceedings of the 4th International Conference on Pipeline Technology, Edited by Rudi Denys, Ostend, Belgium, May 9-13, 2004. |
| [2] | 李晓红, 康勇. 基于应变设计的管道环焊缝缺陷评估[J]. 焊管, 2009, 32(7): 65–67. |
| [3] | 中国石油天然气集团公司. 输油管道工程设计规范: GB 50253-2014[S]. 北京: 中国计划出版社, 2014. |
| [4] | 中国石油天然气集团公司. 输气管道工程设计规范: GB 50251-2015[S]. 北京: 中国计划出版社, 2015. |
| [5] | 张宏, 崔红升. 基于应变的管道强度设计方法的适用性[J]. 油气储运, 2012, 31(12): 952–954. |
| [6] | 李璞, 陶燕丽, 周建. 基于应变设计管道局部屈曲应变极限值的计算[J]. 天然气工业, 2013, 33(7): 101–107. |
| [7] | ANON.Oil and gas pipeline systems:CSA Z662.1-2011[S].Etobicoke, Ontario, Canada:Canadian Standards Association, 2011. |
| [8] | 徐震. X65管线钢的本构关系及失效判据研究[J]. 石油工程建设, 2014, 40(3): 23–27. |



