0 引言
自从Hammerschmidt首次发现天然气水合物会造成管道堵塞以来,水合物堵塞问题始终困扰人们。传统的防治方法有加热或隔热、添加抑制剂和脱水处理等[1],这些方法普遍存在成本高、用量大和污染环境等问题。挪威科技大学的JON STEINAR GUDMUNDSSON于2002年在第四届国际天然气水合物大会上提出了水合物冷流技术 (Cold Flow Hydrate Technology),实质即允许管内生成天然气水合物,但要控制水合物防止其堵塞管道,从而保证输气管道内的安全流动[2-5]。
管道螺旋流输送固体物料作为一种新型的输送方法,有着普通平直流无法比拟的优点。螺旋流在颗粒输送过程中增大了流体与管壁之间的剪切力,使颗粒不易在管壁沉积黏结[6]。螺旋流水合物控制技术最早由常州大学的课题组提出,王树立课题组发明了一种新的管道螺旋流气体水合物输送方法及设备,代替了添加化学试剂等水合物防治方式,有效避免了管道堵塞,提高了天然气运输的安全性和经济性。若将管道平直流动转变为螺旋流动,则必须使用起旋装置改变管道流动的边界,使流动方向发生改变[7-8]。王树立先后提出了一种新型的叶轮式起旋装置、一种新型的导流片式螺旋流起旋器以及一种圆锥翅片式螺旋流起旋器。上述起旋器均具有结构新颖、螺旋效果好及流态衰减慢等特点。通过起旋器在天然气输送管道中产生螺旋流,增大周向流速,提高气流的携带能力,使得水合物颗粒成为悬移质随气体悬浮流动,并在螺旋衰减和悬移颗粒沉降前加设继旋器,以保证气流的携带能力,防止水合物堵塞管道,为管道的安全输送提供保障[9-10]。
综上所述,螺旋流作为一种新型水合物颗粒 (或浆体) 安全输送技术,有必要对螺旋流中颗粒相悬移质的分布情况与输送特性,以及天然气水合物颗粒输送体系的螺旋悬浮流动规律做出进一步研究,以便揭示螺旋气流对水合物的携带特性,从而为输气管道的安全输送提供理论指导。
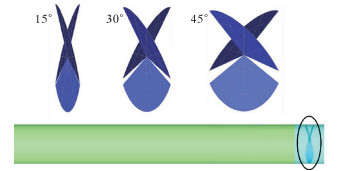
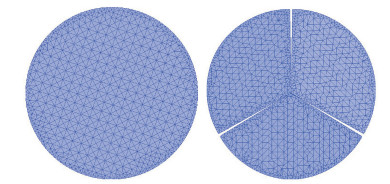
1 建立模型 1.1 几何模型利用ICEM软件建立一条直径D=0.4 m,长L=30 m的水平管道,入口处设置旋角为15°~45°的叶轮,管道及叶轮模型如图 1所示。管道分为2个管段,前管段包含叶轮结构,长0.3 m,采用非结构网格,对叶轮边缘以及管壁处的网格进行加密处理,计算网格如图 2所示。后管段采用结构网格,这样既可以减少数值模拟的误差,又可以提高运算效率,经网格无关性检验后,网格单元数约为120万个。由于不涉及传热,并没有划分边界层网格。计算采用直接坐标系,坐标原点位于管道入口面圆心,Z轴为流动方向,重力沿Y轴负方向。流体介质为天然气,自管道右端向左流动。选取欧拉模型对输气管道进行气固两相三维螺旋流瞬态模拟,采用压力基、隐式求解器[11-13]。
|
| 图 1 管道及叶轮模型 Fig.1 Impeller model |
|
| 图 2 计算网格 Fig.2 Computational grid |
1.2 数学模型 1.2.1 控制方程
连续性方程:
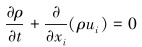
|
(1) |
动量方程:
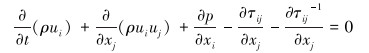
|
(2) |
式中:ρ、u、p分别为气体密度、速度和静压,τij为黏性应力张量,t为时间。
体积分数方程:
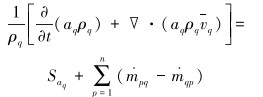
|
(3) |
式中:aq为第q相的体积分数,Saq为源项,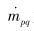

标准κ-ε模型是一个半经验公式,方程为:
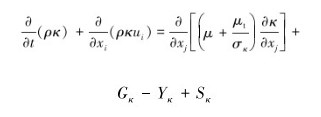
|
(4) |
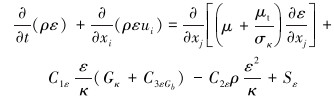
|
(5) |
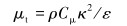
|
(6) |
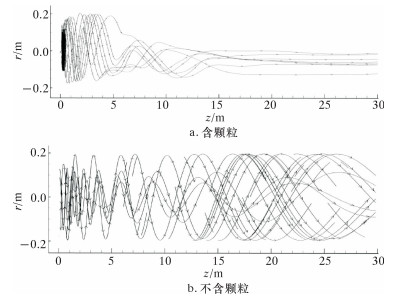
其中:C1ε=1.44,C2ε=1.92,Cμ=0.09,σκ=1.0,σε=1.3。
1.3 初始条件管道直径D=0.4 m,管长L=30 m, 认为水合物浆体的物性为常数;进口边界采用速度入口条件,轴向速度u0=10 m/s;出口边界采用充分发展;天然气密度0.77 kg/m3,水合物颗粒密度915 kg/m3。
水平管中气固两相流温度相同,不存在温差;考虑重力及气固两相之间的滑移边界条件,在每一个单独的试验中,认为水合物颗粒为同一粒径的均质球体,把问题简化为三维、常物性的气固两相流问题。通过改变水合物颗粒粒径、水合物颗粒体积分数、管道倾角及叶轮角度来寻找规律,并设计试验,试验数据如表 1所示。
| 试验序号 | 颗粒体积分数/% | 颗粒粒径/mm | 叶轮角度/(°) |
| 1 | 3 | 0.01 | 15 |
| 2 | 3 | 0.03 | 30 |
| 3 | 3 | 0.06 | 45 |
| 4 | 5 | 0.01 | 30 |
| 5 | 5 | 0.03 | 45 |
| 6 | 5 | 0.06 | 15 |
| 7 | 8 | 0.01 | 45 |
| 8 | 8 | 0.03 | 15 |
| 9 | 8 | 0.06 | 30 |
2 计算结果与分析 2.1 模型验证
将气固两相螺旋流数值模拟结果与上海交通大学实际试验数据进行对比,结果如图 3所示。由图可以看出:雷诺数在 (0.8~2.2)×105范围内,模拟结果和试验结果的误差很小。验证结果显示,用CFD方法可以对气固两相管流进行模拟预测。
|
| 图 3 雷诺数对压降的影响曲线 Fig.3 The effect of Reynolds number on pressure drop |
2.2 气固螺旋流流动规律分析
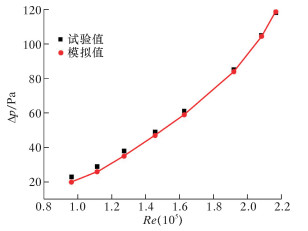
图 4为模拟后水平管螺旋流的流线图。图中z表示距管道轴向的距离;r表示距管道中心的可变半径。分别模拟了含水合物颗粒 (水合物颗粒体积分数为8%,粒径0.06 mm) 以及不含水合物颗粒的情况。由图可以看出,两者的螺旋流在管道中都有明显的衰减,但是含水合物颗粒的螺旋流衰减更为迅速,衰减速率几乎是单相螺旋流的2倍。这说明固体颗粒对螺旋流的流动具有较大的影响,分析气固两相螺旋流的运动规律对将来螺旋流在输气管道中的应用具有重要意义。
|
| 图 4 水平管螺旋流流线图 Fig.4 The spiral flow line in horizontal pipe |
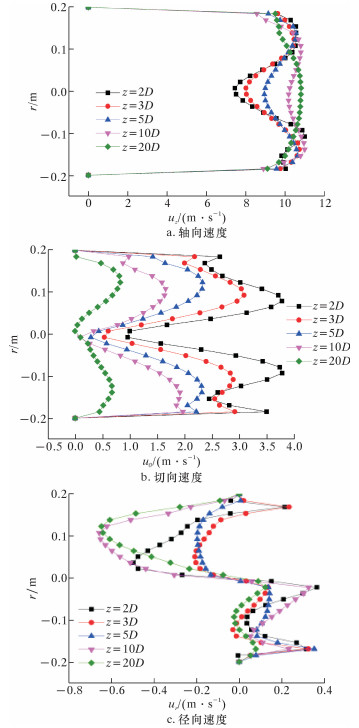
图 5描述了不同截面速度变化情况,表现了管内气固螺旋流的变化和衰减过程。其中uz为轴向速度,uθ为切向速度,ur为径向速度。管道入口轴向速度u0=10 m/s,不带有切向速度;水合物颗粒粒径为0.01 mm,体积分数为3%。由图 5a可以看出:在管道入口2D~10D之间,轴向速度曲线呈现出“双峰”特点,速度峰值出现在距管壁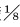
|
| 图 5 不同横截面的速度分布 Fig.5 The velocity distribution at different cross-sections |
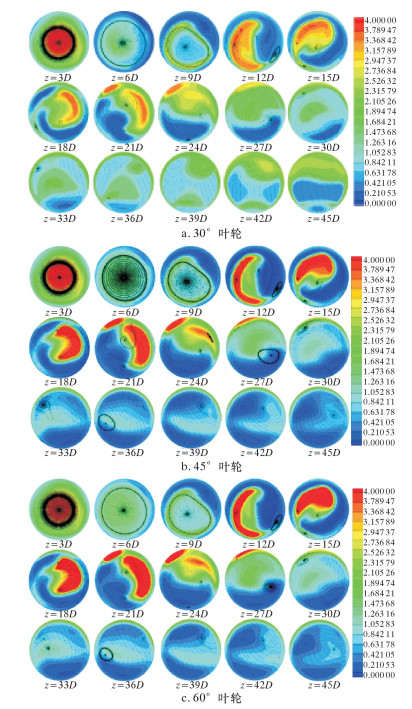
图 6是3种叶轮角度下不同横截面的流线图。气固两相流经过叶轮形成强制涡与自由涡组合的螺旋运动。从图可以看出,叶轮角度为30°时与其他2种角度差距比较明显,螺旋效果也相对较差。当叶轮角度为60°时,螺旋效果最好。在管道入口附近首先出现大尺度漩涡,随后不断破裂为更小的漩涡。由图可以看出:在9D之前螺旋效果很明显,12D时出现了一大一小2个涡并渐渐衰减,到35D处涡基本消失,固体颗粒也会在此处大量聚集。这些涡会加强流体的湍流动能,有利于两相的掺混以及固体颗粒的运移。螺旋流中固体颗粒受离心力作用在管壁附近运动,管轴处则主要由气相构成内旋流。因此认为固体颗粒大多存在于自由涡区域,极少会进入强制涡。
|
| 图 6 3种叶轮角度下不同横截面流线图 Fig.6 The flow line of different cross-sections underthree impeller angles |
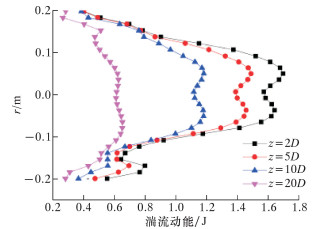
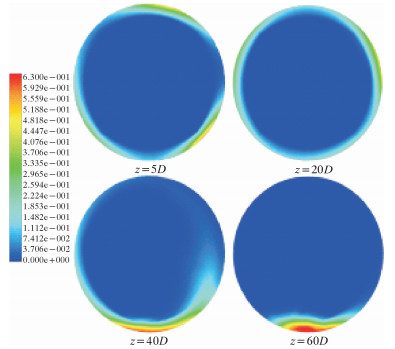
图 7为湍流动能分布曲线。由图可以看出:螺旋流的湍流动能很大同时也衰减较快。管道入口段强制涡区域的湍流动能明显大于自由涡区域,但是湍流动能的衰减很快。图 8是水合物颗粒的体积分数云图。其中入口轴向速度为10 m/s,不带有切向速度;水合物颗粒粒径为0.01 mm,体积分数为5%。由图可以看出:水合物颗粒受离心力作用分布在管壁附近,并没有进入强制涡区域,随后由于旋流强度降低,受重力影响固体颗粒在轴向距离40D处开始出现沉降现象,在60D处沉降现象较为严重。因此叶轮诱导生成螺旋流有利于提高气固两相掺混,避免固体颗粒沉降聚集在管道底部,减少了颗粒与管壁造成的摩阻损失,可以有效提高管道对固体颗粒的输送能力,降低发生管道堵塞的概率。但是湍流动能衰减很快,尤其是管道入口段轴心的强制涡区域具有的湍流动能很大,消耗也很快,然而对于固体颗粒的输送并没有实际意义。因此,如果能通过改进起旋器结构消除或减少强制涡的不利影响,固体颗粒的掺混效果和输送距离都能得到大幅提高。
|
| 图 7 湍流动能分布曲线 Fig.7 The distribution of the turbulent kinetic energy |
|
| 图 8 水合物颗粒体积分数云图 Fig.8 The distribution of the volume fraction of hydrate particles |
2.3 颗粒运动规律的影响因素分析
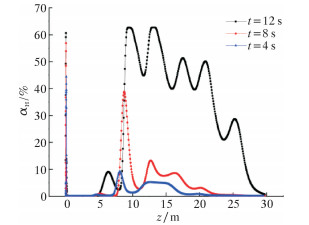
在湿天然气输气管道中经常会出现生成水合物的现象,这些生成的水合物有时可以随气流流动,有时却会聚集沉积在管道壁,甚至造成管道堵塞。堵塞与否主要取决于流体中固态小颗粒如何运动,这是由重力和流体对它的升力所决定的。本节从入口叶轮的角度、水合物颗粒体积分数及粒径大小等几个方面,分析固态颗粒的运动规律和天然气的携带能力。管道中固体颗粒的运动随着时间变化,利用数值模拟试验可以通过水合物颗粒体积分数对颗粒沉降规律进行研究。用αH代表水合物颗粒体积分数,如图 9所示沿管道方向在距管道底部1/4 D取水合物颗粒不同时间的体积分数。发现固体颗粒分布与轴向距离并不是线性关系,而是存在一个峰值。一开始沉积量很小,当到达轴向距离20D~30D之间,沉积高度突然增大。之后管道中沉积高度有所下降逐渐平缓。这可能是因为当颗粒重力超过流体对它的升力后,水合物颗粒开始快速沉积,达到一个沉积高度的峰值。随后由于管道部分堵塞,气体流速增加,同时颗粒体积分数降低,沉积高度有所下降。
|
| 图 9 水合物颗粒分布曲线 Fig.9 Thedistribution of the hydrate particles |
2.3.1 叶轮角度对颗粒运动的影响
在入口轴向速度为10 m/s、水合物颗粒粒径0.01 mm、体积分数8%的工况下对入口叶轮角度的影响进行研究。图 10是轴向距离25D处水合物颗粒分布曲线。图中h代表距管道底部的距离。由图可以看出:3条管道中在距管道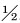

|
| 图 10 不同叶轮角度下水合物体积分数分布曲线 Fig.10 The distribution of the volume fraction of gas hydrateat different impeller angles |
2.3.2 水合物粒径对颗粒运动的影响
在入口轴向速度为10 m/s,水合物颗粒体积分数为5%的工况下对水合物颗粒粒径的影响进行研究。选取的颗粒直径分别为0.01、0.03和0.06 mm。图 11为轴向距离25D处颗粒体积分数分布曲线。从图可看出,当颗粒直径为0.01 mm时,颗粒体积分数随距管底距离迅速下降,在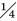
|
| 图 11 不同粒径下水合物体积分数分布曲线 Fig.11 The distribution of the volume fraction of gas hydrateat different particle diameters |
2.3.3 雷诺数对颗粒运动的影响
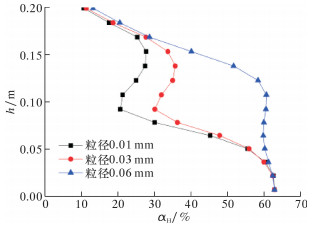
图 12是管道入口25D处颗粒体积分数分布曲线。计算时初始的条件是水合物颗粒的体积分数为8%,颗粒直径0.06 mm。
|
| 图 12 不同雷诺数下水合物颗粒体积分数分布曲线 Fig.12 The distribution of the volume fraction of gas hydrateunder different Reynolds numbers |
由图 12可知,当雷诺数为1.12×105时,气流速度不足以携带固体颗粒,导致了沉积的发生。如果雷诺数达到3.37×105,在管道底部沉积现象大大缓解。因此,流体流速是影响固体颗粒运移和沉积的主要因素。
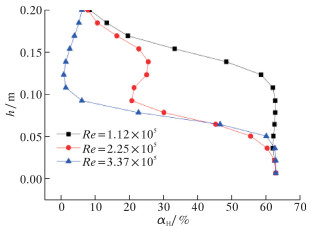
2.3.4 水合物颗粒体积分数对颗粒运动的影响图 13是距离管道底部
|
图 13
距管道底部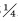 |
3 结论
(1) 螺旋强度较大时,流体速度曲线表现出“双峰”特点;当螺旋强度不大时,流体速度曲线表现出“抛物线”特点。
(2) 螺旋流对液体及固体颗粒有良好的携带能力,但是从试验结果可以看出,当固体颗粒体积分数达到8%时,螺旋流的衰减速度明显增加。
(3) 流体携带能力与起旋器有一定关系,可以通过改变叶轮模型提高流体携带能力。同时,气流的携带能力与颗粒粒径和体积分数成反比,与流体速度成正比。
(4) 气体对固体颗粒的携带作用较差。液固螺旋流中会产生“卷吸”效应,加速固体颗粒向轴心运动。而气固螺旋流中“卷吸”效应不明显,固体颗粒容易聚集沉降。
| [1] | PANTER J L, BALLARD A L, SUM A K, et al. Hydrate plug dissociation via nitrogen purge:Experiments and modeling[J]. Energy & Fuels, 2011, 25(6): 2572–2578. |
| [2] | 宫敬, 史博会, 吕晓方. 多相混输管道水合物生成及其浆液输送[J]. 中国石油大学学报 (自然科学版), 2013, 37(5): 163–167. |
| [3] | ZERPA L E, SALAGER J L, KOH C A, et al. Surface chemistry and gas hydrates in flow assurance[J]. Industrial & Engineering Chemistry Research, 2010, 50(1): 188–197. |
| [4] | 史博会, 全恺, 乔国春, 等. 榆济输气管道水合物冰堵防治措施[J]. 油气储运, 2014, 33(3): 274–278. |
| [5] | 陈鹏, 刘福旺, 李玉星, 等. 水合物浆液流动特性数值模拟[J]. 油气储运, 2014, 33(2): 160–164. |
| [6] | 饶永超, 王树立, 代文杰, 等. 天然气水合物浆体流变性与安全流动边界研究进展[J]. 化工进展, 2015, 34(10): 3551–3556. |
| [7] | 林愉, 雷萍, 李松. 圆管螺旋流形成原理及导叶式局部起旋器的设计[J]. 矿山机械, 2011, 39(12): 54–57. |
| [8] | 李永业, 孙西欢, 阎庆绂. 局部起旋器内部旋流特性试验研究[J]. 水力发电学报, 2011, 30(2): 72–77. |
| [9] | TSAI C W, MAN C, JUNGSUN O H. Stochastic particle based models for suspended particle movement in surface flows[J]. International Journal of Sediment Research, 2014, 29(2): 195–207. 10.1016/S1001-6279(14)60036-6 |
| [10] | 王树立, 饶永超, 张琳, 等. 水平管内螺旋流流动特性研究现状与进展[J]. 太原理工大学学报, 2013, 44(2): 232–236. |
| [11] | 唐军, 高瑞杰. 扬矿管内高速螺旋流的数值模拟与仿真[J]. 江西理工大学学报, 2015(3): 64–68. |
| [12] | LUO G Y, ZHANG M X, TIE-JUN J I. Simulation on the characteristics of flow pattern in sprial up-flow reactor[J]. Journal of Chongqing University, 2007(5): 89–103. |
| [13] | WANG W C, FAN S S, LIANG D Q, et al. Experimental study on flow characteristics of tetrahydrofuran hydrate slurry in pipelines[J]. Journal of Natural Gas Chemistry, 2010, 19(3): 318–322. 10.1016/S1003-9953(09)60072-4 |
| [14] | 王树立, 饶永超, 韩永嘉, 等. 螺旋流发生装置的对比分析研究[J]. 流体机械, 2013, 41(2): 30–38. |
| [15] | 朱莹, 王树立, 史小军. 基于PHOENICS的管道螺旋流数值模拟[J]. 石油机械, 2008, 36(7): 19–22. |
| [16] | CAZAN, R.Dynamics of swirling flows induced by twisted tapes in circular pipes[D].Atlanta Botanical:Georgia Institute of Technology, 2010. |
| [17] | 范卫东, 章明川, 何磊, 等. 管道内气固两相流颗粒浓度和风速测量方法的试验研究[J]. 仪器仪表学报, 2003, 24(1): 13–18. |



