2. 中海油研究总院
2. CNOOC Research Institute
0 引言
受油田采出水量迅速增加和各国环保法律、法规逐渐完善的影响,近年来,用于油田特别是海上油田的油、水、气多相分离技术和方法正在悄然发生着变化,其中最为显著的变化是内联 (In-line)、紧凑 (Compact) 型分离技术的研究和应用逐渐为业内所认可[1]。从目前各类内联紧凑型分离技术的分离原理来看,其最大特点是充分利用了离心力场,在上千倍重力加速度的作用下,分离时间得到了大幅度缩短。在相同处理量下,相关设备的尺寸变得更小,甚至可以直接安装在管线上,形成内联型分离设备[2-7]。与传统分离设备相比,内联型分离设备体积小、质量轻,更容易实现橇装化和集成化,被誉为是解决未来海洋平台水处理瓶颈性问题的关键技术,也将为边际油田开发提供一种有效的解决方案[4, 7]。
轴向涡流分离技术将轴向流动和涡运动巧妙结合,能够实现大处理量单管式快速分离,使真正意义上的内联式紧凑分离成为可能[8-11]。与其他内联紧凑型分离设备不同的是,轴向涡流分离器采用内壁焊接有螺旋形叶片的转鼓作为涡发生器。涡发生器在驱动流经流体形成旋流的同时,还对流体产生一定的轴向推送作用,旋流和轴向运动相耦合形成轴向涡流,因此涡发生器是轴向涡流分离器的关键部件。由于该型涡发生器结构参数较多且各参数间没有明显关系可以遵循,所以设计难度大,至今尚无其结构设计的研究文献。笔者结合理论分析、计算流体动力学 (CFD) 数值模拟和神经网络非线性预测等手段,以轴向涡流分离器分离效率为评价依据对涡发生器关键结构参数进行了分析,最后给出了其优选方法。并利用优选后结构参数设计的轴向涡流分离器进行现场试验研究,验证了CFD数值模拟结果的可靠性。
1 涡发生器内部流场分析轴向涡流分离器主要由高速旋转的涡发生器、静止的分离机筒和轻相收集管等组成,其原理如图 1所示。涡发生器为内壁固定焊接有一定数量螺旋形叶片的转鼓,叶片的长度和高度均小于转鼓的长度和半径。叶片安装在转鼓入口端,有叶片的区域称为涡发生器的加速区,后端无叶片的区域称为涡发生器的稳流区。高度较小的叶片又将加速区分为外环叶片区和中心中空区。分散相收集区为与涡发生器处于同一轴线上的静止分离机筒,机筒内部中心线末端安装有轻相收集管。为便于计算,以入口中心为原点,轴向方向为z轴,垂直于z轴的方向为r轴建立柱坐标系,如图 1所示。
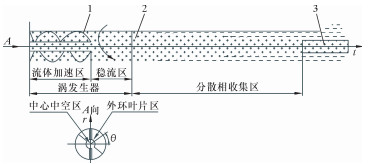
|
| 图 1 轴向涡流分离器原理示意图 Fig.1 Schematic diagram of axial vortex separator 1—螺旋叶片;2—静止分离机筒;3—轻相收集管。 |
1.1 分离死区及避免方法
轴向涡流分离器工作过程中,自左端进入涡发生器的待分离混合液首先进入加速区,在转鼓和叶片共同作用下外环叶片区流体快速形成涡运动。在图 1所示的柱坐标系中,根据离心力Stokes公式,对于直径为d0,位于涡流中径向r处的分散相油滴受到的向心浮力Fp为:
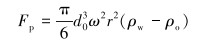
|
(1) |
式中:ω为涡发生器的角速度,ρw为连续水相的密度,ρo为分散油相的密度。
当分散相油滴以一定的径向速度向轴心区域运移时,分散相和连续相间就产生了相对运动。在连续相液体黏性作用下,连续相介质会对分散相油滴的运移产生阻碍作用,其介质阻力 (拖曳力)Fd为[12-13]:
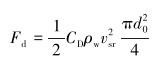
|
(2) |
式中:vsr为分散相油滴相对连续相的滑移速度,CD为拖曳系数。
分离过程中向心浮力指向轴心而拖曳力由轴心指向机筒壁面,当向心浮力大于拖曳力时,轻相向中心运移而重相流向壁面。当流体的角速度ω为定值,由式 (1) 和式 (2) 可知,轻相油滴所受的向心浮力随其所在半径r的减小而降低,而反向拖曳力的大小与位置无关。在近轴心区,当向心浮力小于拖曳力时,重相组分不再向壁面运移。停留在轴心附近的重相组份势必阻碍轻相向轴心区域的汇集,该区域被称为分离死区,分离死区的存在使得离心分离设备的分离效率大大降低[14-15]。
为了避免分离死区的影响,迫使轴心区重相组份流出的方法被大多数研究者所采用[16-17]。如,T.YAMAMOTO等[15]在涡发生器中心安装实心轴或涡破除器 (Vortex breaker),迫使轴心区重相流出,并在实心轴的末端形成低压区,从而避免分离死区的影响。J.Y.JIAO等[14]将多根细长管绕固定中心圆柱焊接成管束式涡发生器,用于分离空气中的微尘,试验和CFD数值模拟均表明:待分离气体经高速旋转的管束后可形成稳定的涡环,进而可以高效地分离出空气中粒径小于10 μm的微尘。通过强制手段迫使轴心区域重相组分流出的方法固然可以避免分离死区,然而在实心轴的末端流体会形成垂直于流体流动方向的局部脱离涡,其势必会对流体主涡的运动造成扰动。
轴向涡流分离器工作时,高速旋转的螺旋形叶片对流经的流体有一定轴向推送作用,使外环叶片区流体轴向速度增加,进而增加了外环叶片区流体的流量。分离过程中入口流量保持不变,当外环叶片区流量增加时,中心中空区流体流量势必降低,以保证流体的质量守恒。因此在渐变螺旋叶片的轴向推送作用下,中心中空区流体被吸入至外环叶片区,从而在中心区形成一个低压和低轴向速度区。当该区域内流体的压力和轴向速度小于0时,待分离混合液将以涡环形式流出涡发生器的加速区,从而在不对涡运动造成任何扰动的前提下避免分离死区;同时,还可以增加机筒壁面到轴心的压力降梯度。由此可见,轴向涡发生器的关键零件为焊接在转鼓内表面三维螺旋形叶片,为使流体进入涡发生器时不产生扰动,将叶片设计为渐变螺旋形,其入口导程角为90°。
1.2 中心区流体轴向速度分析设渐变螺旋形叶片上任意点处流体牵连速度矢量为u,相对于叶片的相对速度矢量为w,忽略叶片的厚度,并假设叶片数量为无穷多个,则在外环叶片区有如图 2所示的速度矢量关系。
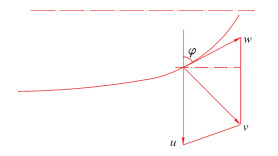
|
| 图 2 叶片上任意点处流体的速度矢量关系 Fig.2 The velocity vector at any given point on thehelical blades |
根据图示矢量三角形有外环叶片区流体的绝对速度矢量v可表示为:
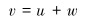
|
(3) |
利用螺旋桨升力理论对渐变螺旋形叶片的轴向推力进行估算,则其产生的理论轴向升力系数Cy0满足下式:
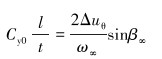
|
(4) |
式中:l为叶片的最大弦长,t为叶片数量,ω∞为来流速度,β∞为来流速度和叶片中心线的夹角,Δuθ为外环叶片区流体切向速度的增量,根据螺旋桨升力计算公式,Δuz为:
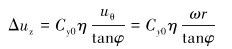
|
(5) |
式中:φ为渐变螺旋形叶片的出口处导程角,η为叶片的泵送效率。
忽略离心力对轴向速度的影响,外环叶片区流量的增量ΔQ可以由式 (5) 计算得出。
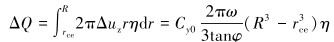
|
(6) |
设入口流量不变,则中心中空区减少的流量亦为ΔQ。由式 (4) 和式 (6) 可以计算出中心中空区流体在加速区出口处的平均轴向速度uzc0为:
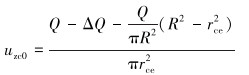
|
(7) |
为彻底避免分离死区对涡发生器分离性能的影响,uzc0的值应小于等于0,此时流体将以涡环的形式流入稳流区,进而进入轻相收集区。在轻相收集区,轻相油滴在向心浮力和径向压力梯度的双重作用下快速向中空的轴心区域汇聚,且不会受到任何阻碍。
由式 (6) 和式 (7) 可见,影响涡发生器内流体流速的关键结构参数为转鼓内径、中空区直径和叶片出口导程角,而这些参数又与转速和流量等操作工艺参数相关联。为简化设计过程,首先确定要设计的轴向涡流分离器的流量,并依此选定转鼓内径,将这2个参数设为固定值。为避免分离死区将uzc0的值设为临界值“0”,则有中空区直径、叶片出口导程角和涡发生器转速等3个未知参数,而可用方程仅有式 (6) 和式 (7)。
另外,叶片长度决定了涡发生器加速区的长度,进而影响待分离混合液在涡发生器中被加速形成涡流的时间,而此参数在无穷多个无厚度叶片的假设条件已经被忽略掉。由此可见,理论分析方法可以确定涡发生器的关键结构参数,但是,无法准确计算这些参数的具体值。为此,笔者在理论分析的基础上用CFD数值模拟和BP神经网络相结合的方法对其进行优选。
2 数值模拟随着基于有限体积法的数值模拟技术和计算机软、硬件的迅速发展,复杂流场CFD数值模拟的可行性和可操作性越来越大,大量的研究已经证明,常用的商业CFD数值模拟软件完全可以对管道中多相流的涡运动过程进行较为精确的模拟计算,模拟结果对流体机械关键零部件结构尺寸的优选具有较大的指导意义[1, 18-19]。笔者采用商业软件ANSYS FLUENT 14.0对轴向涡流分离器的分离过程进行三维数值模拟,以分析不同涡发生器结构参数和转速下的分离效率,并以此作为神经网络学习的样本。
2.1 模拟方案将轴向涡流分离器的处理量设为6 m3/h,并依此将转鼓的内径选定为60 mm,则中空区直径可由叶片高度决定,如图 1所示。为此, 渐变螺旋形叶片的长度、高度和出口导程角等3个参数是涡发生器的关键结构参数,根据理论分析初步确定这3个参数的变化范围,并等分为7等份,所得的3因素7水平值见表 1。
| 水平个数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 出口导程角/(°) | 65 | 68 | 70 | 72 | 74 | 76 | 80 |
| 长度/mm | 130 | 140 | 150 | 160 | 170 | 180 | 190 |
| 高度/mm | 18.5 | 19.5 | 20.5 | 21.5 | 22.5 | 23.5 | 24.5 |
对表 1中3因素7水平的所有组合进行建模分析,工作量无疑太过巨大,为在有限的模拟量下使样本值更加具有针对性,笔者采用正交设计的方法对这些因素和水平值进行优化组合,正交设计后的组合方案共有20组。
根据式 (6) 和式 (7) 可知:当转鼓内径和流量固定时,涡发生器结构参数还与转速有着密切的关系。为此,模拟将以正交设计得到的20参数组合为基础,就每组基础参数组合下不同转速的物理模型进行模拟计算。转速取值1 600、1 800、2 000、2 200、2 400、2 600、2 800和3 000 r/min等8种,由此可以得到160组模型。其他非关键的操作工艺参数如分流比和入口含油污水的含油质量浓度等均被设为常数,分别为10%和1 288 mg/L。
2.2 物理模型设轴向涡流分离器的长度为320 mm,渐变螺旋形叶片的厚度为3 mm,长度、高度和出口导程角的取值见表 1;静止分离机筒最大直径为60 mm,长度为1 000 mm,水相出口直径为40 mm;轻相收集管为圆柱形,内径为20 mm,收集管壁厚2 mm。设温度恒定为20 ℃;介质为油水混合物,连续相介质为水,密度为1 000 kg/m3,黏度为1.0 mPa·s;分散相介质为自定义原油,密度设为880 kg/m3,黏度设为5.4 mPa·s,油滴粒径为50 μm。
根据轴向涡流分离器的结构将其划分为6个部分,从涡发生器的加速区开始划分网格,其他部分均以加速区的网格为基础进行划分。加速区沿叶片的边界对网格进行加密,并将中心中空区的网格设置为网格密度最大的区域。
2.3 计算模型及边界条件轴向涡流分离器内的流动为非稳态、强湍流的高强度涡运动,非稳态的湍流模型,如大涡模型 (LES) 和直接模拟模型 (DNS),无疑最适合此类模拟。一些研究者通过比较数值模拟和试验结果认为:在模拟类似于水力旋流器分离过程中这类复杂流场时,LES和DNS模型需要高性能的计算机,且模拟时间长,而其精度与常规κ-ε模型和雷诺应力模型 (RSM) 等湍流模型基本相同[20]。为此,计算时间较短的κ-ε模型和雷诺应力模型 (RSM) 在模拟强湍流的高强度涡运动中得到了广泛应用。其中RSM模型较为严格地考虑了流线的弯曲、漩涡、旋转和张力的快速变化过程,对于复杂的旋流流场具有较高的预测精度,因此在水力旋流器的数值模拟中应用较多[20-22]。
为了准确模拟轴向涡流分离器内的流场,计算其分离效率,笔者采用了全尺寸的三维物理模型和双精度隐式求解方法,并假设分离过程中待分离混合液为稳态流动。轴向涡流分离器内流场的主要运动形式为涡运动,因此选择对涡运动计算精度更高的算法:压力计算方程为PRESTO!(PREssure Staggering Option) 算法,压力-速度耦合计算方程为SIMPLE (semi-implicit pressure linked equations) 算法,其他方程均采用高阶的QUICK算法[20, 23]。初始状态下入口、水相出口和油出口分别设为质量流量入口和质量流量出口。选择多相流模型为Mixture模型,湍流模型为RSM模型,入口处油组份均匀分布在水中,油滴的平均粒径设为50 μm。涡发生器段流体按照旋转坐标系的方法进行设定,并假设入口完全对称,且壁面无滑移,相应的壁面设为旋转壁面,壁面转速和旋转的坐标系转速一致。静止分离机筒和涡发生器间交界面处设置为内部面 (interior face),机筒壁面设为固定无滑移壁面。
2.4 网格独立性验证物理模型中叶片和转鼓在入口端面处形成较小的扭曲尖角,且转鼓和叶片间形成的流道扭曲也较为严重,因此采用非结构网格划分时,涡发生器加速区网格的畸形因子较大,其中畸形因子大于0.95的网格约占总网格的2%。而沿叶片的螺旋方向进行拉伸形成结构网格畸形因子较小,最大畸形因子不大于0.65。
为进一步考察结构网格划分模式下网格数量对数值模拟结果的影响,在50万至150万网格之间,划分了6种网格数的模型,其网格质量见表 2。由表可见,各模型均具有较好的网格质量,最大畸形因子仅为0.62,且大部分网格为质量较高的六面体网格,网格畸形因子数在0.0~0.3之间的网格数占总网格数的91%以上。
| 模型序号 | 网格数量 | 畸形因子占比/% | 最大变形量 | 最大畸形因子 | 最大长宽比 | |
| 0.0~0.3 | 0.3~0.6 | |||||
| A | 520 581 | 91.49 | 8.51 | 0.35 | 0.57 | 12.06 |
| B | 689 434 | 94.03 | 5.97 | 0.30 | 0.61 | 12.73 |
| C | 740 042 | 93.80 | 6.20 | 0.38 | 0.58 | 8.32 |
| D | 873 821 | 93.71 | 6.29 | 0.33 | 0.52 | 10.71 |
| E | 1 007 486 | 94.75 | 5.25 | 0.25 | 0.48 | 8.43 |
| F | 1 471 610 | 94.12 | 5.88 | 0.30 | 0.53 | 9.57 |
关键结构参数取值为:叶片出口导程角74°、长度160 mm、高度20 mm、转速2 000 r/min,此时,不同网格密度模型模拟结果见表 3。由表可见,各模型模拟的质量守恒性随网格密度的增加而增加,D、E、F模型质量守恒性最好,分散相的质量流量误差均小于1%,其中E模型误差最小仅为0.06%。就分离效率而言,D、E、F 3模型模拟结果也比较接近。
| 模型 序号 |
入口含油 质量浓度/ (mg·L-1) |
水出口含油 质量浓度/ (mg·L-1) |
混合相质 量流量误 差/% |
分散相质 量流量误 差/% |
分离效 率/% |
| A | 960 | 196.5 | 0.000 94 | 7.29 | 79.5 |
| B | 960 | 207.8 | 0.000 02 | 1.90 | 78.3 |
| C | 960 | 207.2 | 0.000 68 | 5.30 | 78.4 |
| D | 960 | 259.8 | 0.000 02 | 0.17 | 72.9 |
| E | 960 | 285.0 | 0.000 01 | 0.06 | 70.3 |
| F | 960 | 264.0 | 0.000 13 | 1.00 | 72.4 |
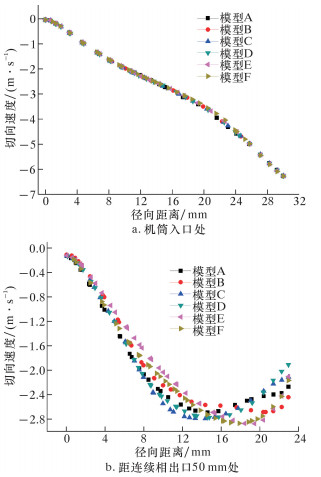
机筒入口和距出口50 mm处不同网格密度模拟的流体切向速度分布如图 3所示。不同网格密度模型下,机筒入口处流体的切向速度分布保持一致,如图 3a所示。在距连续相出口处50 mm处,模型E、F切向速度保持一致,而其他模型切向速度值均有不同程度的偏差,如图 3b所示。因此当网格数超过100万后,模拟精度就不再与网格的密度相关。综合以上因素,模拟中选择E模型,模型的网格单元数量及网格质量参数如表 2所示。
|
| 图 3 不同网格密度模型下流体的切向速度分布图 Fig.3 The tangential velocity profile of the fluid underdifferent mesh density |
3 基于BP神经网络的模拟结论分析
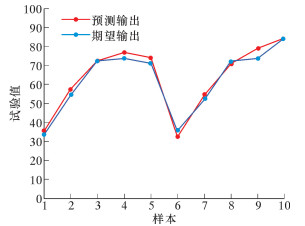
采用Fluent对由正交设计所提供的160组模型进行模拟,得出各组参数下轴向涡流分离器的分离效率,并做记录。就模拟所得的160组数据,选取其中150组作为BP神经网络的训练样本,剩余10组为检测样本。BP神经网络模型中输入参数为叶片高度、长度和出口导程角等关键结构参数以及涡发生器的转速,输出参数为分离效率。基于Matlab神经网络工具箱完成BP神经网络程序编写,训练函数为traincpg函数,隐含层节点数为14个,10组检测样本的预测值和样本实际值的变化趋势如图 4所示。
|
| 图 4 预测值和样本值间的变化趋势 Fig.4 The predicted values and the sample values |
由图 4可见,2条曲线之间的符合度较好,平均相对误差为0.042,最大误差为0.075。
3.1 模拟结果总体分析首先将涡发生器转速和分离效率2个参数作为控制参数,而将叶片高度、长度和出口导程角作为输出值。当分离效率为90%,转速在1 800~3 200 r/min之间变化时,BP神经网络预测的最优参数组合随其转速变化的取值见表 4。由表可见,高分离效率下,随转速的增加,叶片出口导程角逐渐增加,而叶片长度和高度则逐渐减小。
| 序号 | 转鼓转速/ (r·min-1) |
叶片出口导 程角/(°) |
叶片长 度/mm |
叶片高 度/mm |
| 1 | 1 800 | 68.717 5 | 163.814 6 | 21.602 7 |
| 2 | 1 900 | 69.575 1 | 159.915 5 | 21.435 9 |
| 3 | 2 000 | 70.611 7 | 156.739 1 | 21.210 7 |
| 4 | 2 100 | 72.337 1 | 157.325 2 | 20.678 3 |
| 5 | 2 200 | 73.407 1 | 159.995 4 | 20.424 1 |
| 6 | 2 300 | 73.296 4 | 162.464 4 | 20.670 5 |
| 7 | 2 400 | 72.982 2 | 163.979 5 | 20.974 7 |
| 8 | 2 500 | 72.869 9 | 163.717 5 | 21.171 6 |
| 9 | 2 600 | 73.072 4 | 161.837 8 | 21.229 0 |
| 10 | 2 700 | 73.523 5 | 157.846 7 | 21.138 4 |
| 11 | 2 800 | 74.071 7 | 150.504 0 | 20.885 4 |
| 12 | 2 900 | 74.929 0 | 142.213 5 | 20.546 2 |
| 13 | 3 000 | 76.344 5 | 137.162 8 | 20.243 2 |
| 14 | 3 100 | 78.032 5 | 135.185 4 | 19.966 6 |
| 15 | 3 200 | 80.171 8 | 135.874 0 | 19.567 7 |
结合式 (6) 和式 (7) 可知:当中心低压区流体的轴向速度保持0不变时,渐变螺旋叶片出口导程角的正切值与转速成反比,叶片高度的三次方与转速成正比,理论分析结果与BP神经网络预测结果一致。另外,叶片长度的预测值随转速增加而逐渐减小的趋势表明,所有其他参数不变时仅增加叶片的长度,叶片对流体的轴向推送作用也随之增加。
当处理量一定时,涡发生器关键结构参数随转速变化而变化的特性有利于根据特定待分离混合液性质选择转速,进而确定其最优结构参数组合。根据现场试验目标油田 (中原油田) 生产水特性,选择轴向涡流分离器的处理量为6 m3/h、转速为2 300 r/min。由表 4可得最优结构参数组合为:叶片出口导程角73.3°、叶片长度162.5 mm、叶片高度20.7 mm。
3.2 单影响因素分析为更加精确地确定涡发生器最优结构参数组合,以叶片的长度、高度、出口导程角和转速等4个参数作为BP神经网络控制参数,而将分离效率作为输出值。保持4个参数中的3个不变,预测分离效率随其中一个参数的变化趋势,以分析各个参数对轴向涡流分离器分离性能的影响,不同参数变化时,预测的分离效率曲线如图 5所示。

|
| 图 5 预测的分离效率随不同参数变化的曲线图 Fig.5 The relation curve between separation efficiencyand different parameters |
其他参数不变,随叶片长度的增加,分离效率呈先缓慢增加而后迅速减小的趋势,当叶片长度在165~175 mm之间时,分离效率最高,随后迅速降低,如图 5a所示。分离效率随叶片高度的变化曲线由图 5b所示,当叶片的高度在19.5~24.5 mm之间时,分离效率稳定在最高区,增大或减小叶片高度,分离效率均迅速下降。分离效率随叶片出口导程角增加的变化曲线如图 5c所示,分离效率先迅速增加,而后缓慢降低,当出口导程角在68°~72°之间时,分离效率最高。
由以上分析可知,当转速为2 300 r/min时,最优结构参数组合可选为:叶片长度170.0 mm、叶片高度21.5 mm、叶片出口导程角72°。
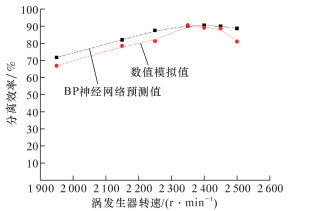
为进一步判断以该组结构参数为基础构建的轴向涡流分离器分离性能,利用BP神经网络对该组结构参数下分离效率随转速变化的关系进行分析。分离效率随转速变化的曲线如图 5d所示。由图可见,在最优参数组合下,分离效率随转速的增加呈先缓慢增加,然后迅速下降的趋势。当转速在2 300~2 600 r/min之间时,分离效率最高。在最佳涡发生器转速范围内,分离效率的CFD数值模拟值和BP神经网络预测值如图 6所示。由图可见,预测结果和CFD数值模拟结果基本一致,最大误差仅为8.67%。
|
| 图 6 分离效率的数值模拟值和BP神经网络预测值比较 Fig.6 Comparison of the numerical simulation values and theBP neural network prediction values of separation efficiency |
4 现场试验研究
现场试验在中原油田采油一厂五区79块计量站进行。试验中轴向涡流分离器通过闸阀与三相分离器水相出口连接,分离后的油、水两相再汇集到原管线上。现场试验所用设备是根据中原油田所提供的污水物性参数,专门研制的BIPTVAS-Ⅱ型轴向涡流分离器,其关键结构参数如下:转鼓长320 mm,转鼓内径60 mm;叶片长170 mm,高21.5 mm,出口导程角72°;锥段机筒长800 mm,机筒锥角1.43°。
4.1 试验方案现场试验研究拟围绕入口流量和涡发生器转速等关键操作工艺参数进行,相关的参数取值见表 5。由于接入点的总来液量较小,最大流量不大于6 m3/h,且计量站管汇处流量和压力波动较大,为保证不影响下游生产,试验中只能根据现场流量的变化情况调整试验步骤。为尽量缩短现场试验时间,提高现场试验数据的有效性,首先根据理论分析结果对所需要研究的操作工艺参数进行优选。根据式 (6) 和式 (7) 可知,影响涡发生器中空区流体轴向速度的关键操作工艺参数为流量和转速,因此现场试验中仅对流量和转速2个因素进行测试,分流比固定设为10%。
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 流量/ (m3·h-1) |
2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | 6.0 |
| 转速/ (r·min-1) |
900 | 1 200 | 1 500 | 1 800 | 2 100 | 2 400 | 2 700 | 3 000 |
4.2 试验结论分析 4.2.1 试验数据概览
轴向涡流分离器入口、出水口污水的含油质量浓度及其分离效率直方图如图 7所示。当来液含油质量浓度大于4 000 mg/L时,出水口污水含油质量浓度小于960 mg/L,平均分离效率为83%,最高分离效率达90%以上;当来液含油质量浓度小于4 000 mg/L时,出水口污水含油质量浓度可降至300~800 mg/L,平均除油率为80%。总体而言,分离效率随来液含油质量浓度的增加而略有提高,当来液含油质量浓度降低50%时,分离效率仅降低了3.6%,因此来液含油质量浓度的影响很小,可以忽略。
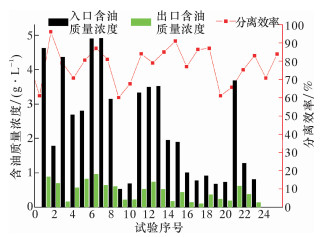
|
| 图 7 轴向涡流分离器现场试验分离效率直方图 Fig.7 The separation efficiency histogram of the axialvortex generator in field test |
4.2.2 转速对分离效率的影响
当入口流量为3、4、5和6 m3/h,分流比为10%时,轴向涡流分离器分离效率的现场试验测试值和CFD数值模拟值随转速的变化关系如图 8所示。由图可见,当入口流量大于3 m3/h时,不同入口流量下分离效率随转速的增加均有先增加而后降低的趋势;CFD数值模拟值与现场试验测试值非常接近,平均误差仅为2.46%,且在不同转速下分离效率的变化趋势也基本一致。
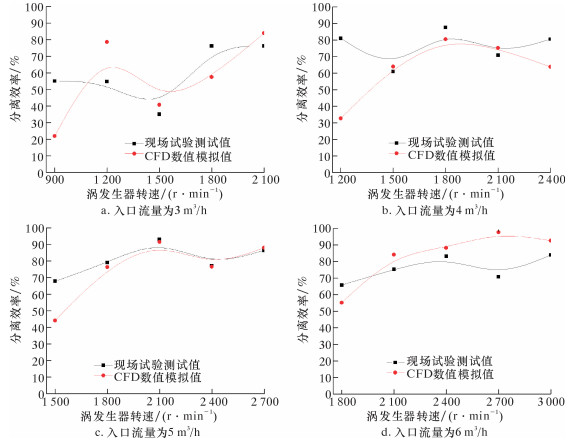
|
| 图 8 不同入口流量时分离效率随涡发生器转速的变化曲线 Fig.8 The effects of vortex generator rotation velocity on the separation efficiency under different inlet flow rates |
分析CFD数值模拟和试验结果间的误差出现位置不难看出,最大误差仅出现在低转速区,最大误差为60%。在误差较大的取样点处,现场试验分离效率远高于CFD数值模拟的分离效率,也就是说试验中低转速工况下轴向涡流分离器也具有较好的分离效率。造成该误差的主要原因可能是试验中污水中含有部分较大粒径的分散相油滴,低转速工况下这部分油滴也可以被分离出,而CFD数值模拟中分散相油滴粒径被设为50 μm的固定值,转速较低时分离效率也较低。而在高转速工况下,这部分大粒径分散相油滴产生的影响较小,因而误差主要出现在低速区。总体而言,CFD数值模拟的精度较高,其结论可以作为设计的评价依据。
4.3 流量对分离效率的影响不同流量下峰值分离效率和涡发生器转速的变化趋势如图 9所示。比较图 8和图 9可见,峰值分离效率随流量的增加呈快速增加而后缓慢下降的趋势,流量在4~5 m3/h时的分离效率最高,可达90%以上;此时随转速的变化,分离效率的峰值区间较宽,即轴向涡流分离器的稳定性较好。另外,随流量的增加,最高分离效率所对应的转速呈线性增加。
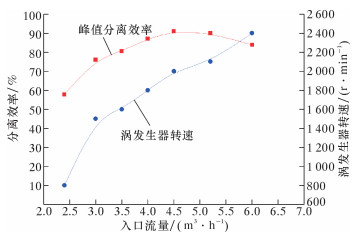
|
| 图 9 不同流量下峰值分离效率与转速的变化趋势图 Fig.9 The curve of the peak separation efficiency and thevortex generator rotation velocity at different flow rates |
将涡发生器加速区流体的中心流率定义为中空区流体流量Qr与总流量之比,则中心流率ε可表示为:
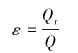
|
(8) |
根据式 (6) 可计算出中空区流体的流量Qr为:
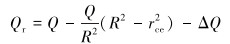
|
(9) |
根据式 (8) 和式 (9) 计算出峰值分离效率时的中心流率如表 6所示。由表中数据可见,峰值分离效率时中心流率在0值附近,即此时涡发生器加速区中心中空区流体处于回流的临界状态,与理论分析中的假设相符。由此可见,中心低压和低轴向速度区对轴向涡流分离器的分离性能有较大的影响,当中心流率在临界值0附近时,分离效率最高。
| 入口流量/ (m3·h-1) |
最优分离 效率/% |
最优分离效率下的转 鼓转速/(r·min-1) |
中心流 率/% |
| 3.0 | 76.0 | 1 500 | -4.22 |
| 3.5 | 80.5 | 1 600 | -1.38 |
| 4.0 | 84.0 | 1 800 | -1.05 |
| 4.5 | 91.0 | 2 000 | -0.71 |
| 5.0 | 87.0 | 2 100 | 0.72 |
| 6.0 | 83.0 | 2 400 | 1.83 |
设峰值分离效率时的中心流率为0,根据式 (7) 有,涡发生器转速随入口流量的减小而降低。由式 (1) 可以看出,分离过程中轻相油滴受到的向心浮力与转速的平方成正比,因此在低流量和低转速条件下,分离过程的水力停留时间增加,但分散相油滴受到的向心浮力较小。当增加的水力停留时间短于因向心浮力下降而增加的分散相油滴向中心汇聚的时间时,分离效率开始下降。当入口流量为2.5 m3/h时,最优涡发生器转速为800 r/min,对应的分离效率仅为66%。随着流量和转速的增加,涡流中分散相油滴受到的向心浮力也逐渐增加,增加的向心浮力使分散相油滴向中心汇聚的时间减小。当分散相油滴向中心汇聚的时间减小值大于因入口流量增加而减小的水力停留时间时,轴向涡流分离器的分离效率逐渐升高。当入口流量在4.5~5.0 m3/h之间、转速为2 000 r/min左右时,轴向涡流分离器的分离效率最高, 为91%。流量继续增加,水力停留时间的减小值长于分散相油滴向轴心汇聚时间减小值时,分离效率开始随之降低;同时较高的转速下,进入涡发生器的流体切向速度迅速增加,在涡发生器入口处将产生较强的湍流和较大的剪切应力,强湍流和大剪应力有可能使较大的分散相油滴发生破碎,因此当入口流量为6 m3/h时,CFD数值模拟的分离效率仍然高于90%,而现场试验测试值则降至83%。
综合分析可知:中心流率是影响轴向涡流分离器分离性能的关键,工作时应保持其处于临界值0附近,若流量保持不变,则结构参数可以根据转速进行确定;而当结构参数保持不变时,转速随入口流量的增加而增加。因此,为使轴向涡流分离器的分离效率高,且性能稳定,应根据具体使用环境选择转速范围,进而完成涡发生器的结构设计。
5 结论(1) 根据轴向涡流分离器内涡的形成过程和避免分离死区的方法,确定了涡发生器关键结构参数为渐变螺旋形叶片长度、高度和出口导程角,并对不同结构参数下的物理模型进行了CFD数值模拟。
(2) 针对给定待分离混合液的物性参数,BP神经网络的预测结果表明,渐变螺旋形叶片的最优参数组合为:长度170 mm、高度21.5 mm、出口导程角72°。在最优涡发生器结构参数下,当转速在2 300~2 600 r/min之间时分离效率最高,最高可达90%,且BP神经网络的预测值和CFD数值模拟值非常接近,最大误差仅为8.67%。
(3) 利用预测结果设计了BIPTVAS-Ⅱ型轴向涡流分离器,并利用该型分离器进行了现场试验研究,试验结果表明:所设计的轴向涡流分离器具有较高的分离效率和较好的稳定性,处理量为4~5 m3/h时,平均分离效率可达80%以上;且试验结果与CFD数值模拟结果非常接近,平均误差仅有2.46%。因此CFD数值模拟结论具有很高的可信度,完全可以直接作为神经网络学习样本用,从而大幅度减少试验研究,降低研究成本。
(4) 综合分析可知,以中心流率为依据的涡发生器关键结构参数设计的理论计算方法与BP神经网络预测结果以及现场试验结果相一致,均表明当中心流率在临界值0附近时,轴向涡流分离器的分离效率最高。此时,涡发生器的关键结构参数与转速和流量有着密切的关系。因此,要保持轴向涡流分离器在最佳的工作状态,必须根据特定待分离混合液的物性参数和应用环境,先确定涡发生器的转速合理范围,然后再进行轴向涡流分离器的设计。
| [1] | SIMMONS M J H, KOMONIBO E, AZZOPARDI B J, et al. Residence time distributions and flow behaviour within primary crude oil-water separators treating well-head fluids[J]. Chemical Engineering Research and Design, 2004, 82: 1383–1390. 10.1205/cerd.82.10.1383.46735 |
| [2] | WESTRA R, HANNISDAL A, AKDIM M R.Compact separation technologies and their applicability for subsea field development in deep water[C]//Offshore Technology Conference.OTC, Houston, Texas, USA, 2012:1-12. |
| [3] | SCHOOK R, DANNY T.Debottlenecking of mature field production through the use of very compact and efficient separation equipment[C]//Offshore Technology Conference.Houston, Texas, USA, 2011. |
| [4] | VERBEEK P, Al-MOOSANI A.In-line separation pilot to support produced water injection[C]//International Petroleum Technology Conference.Doha, Qatar, 2009:1-7. |
| [5] | FANTOFT R, AKDIM M R, MIKKELSEN R, et al.Revolutionizing offshore production by inline separation technology[C]//SPE Annual Technical Conference and Exhibition.Florence, Italy, 2010:1-12. |
| [6] | JAISEN N.Improving efficiencies in water-based separators using mathematical anlaysistool[D].Blacksburg:the Virginia Polytechnic Institute and State University, 2000. |
| [7] | SCHOOK R, ASPEREN V V.Compact separation by means of inline technology[C]//SPE Middle East Oil and Gas Show and Conference.Kingdom of Bahrain, 2005:1-7. |
| [8] | BELLA A D, ANTHONY M M.Apparatus with voraxial separator and analyzer:6224063B1[P].2001-05-01. |
| [9] | RICHTER H E.Method and apparatus for separating fluids having different specific gravities:5084189[P].1992-01-28. |
| [10] | DIBELLA A, ANTHONY M.Voraxial filtration system with self-cleaning auxiliary filtration apparatus:7727386B2[P].2010-06-01. |
| [11] | MICHAEL M.Voraxial filtration system with self-cleaning auxiliary filtration apparatus:2005/0109684 A1[P].2005-05-26. |
| [12] | GOMEZ C H.Oil-water separation in liquid-liquid hydrocyclones (LLHC)-experiment and modling[D].Tulsa:The University of Tulsa, 2001. |
| [13] | JOSE G, GOMEZ L E, MOHAN R S, et al. Mechanistic modeling of solids separation in solid/liquid hydrocyclones[J]. Facilities & Construction, 2010(5): 121–135. |
| [14] | JIAO J Y, ZHENG Y, SUN G G. Numerical simulation of fine particle separation in a rotational tube separator[J]. China Paretic, 2005, 3: 219–223. 10.1016/S1672-2515(07)60190-0 |
| [15] | YAMAMOTO T, WATANABE N, FUKUI K, et al. Effect of inner structure of centrifugal separator on particle classification performance[J]. Powder Technology, 2009, 192: 268–272. 10.1016/j.powtec.2009.01.003 |
| [16] | KEGGE S J.Numerical simulation of an axial hydrocyclone[D].Delft:Technische Universiteit Delft, 2000. |
| [17] | GAO Q.Evolution of eddies and packets in turbulent boundary layer[D].Minneapolis:The University of Minnesota, 2011. |
| [18] | ERDAL F M.Local measurements and computational fluid dynamics simulations in a gas liquid cylindrical cyclone separator[D].Tulsa:The University of Tulsa, 2001. |
| [19] | Ventikos Y, Sotiropoulos F. The three-dimensional structure of confined swirling flows with vortex breakdown[J]. J.Fluid Mech, 2001, 426: 155–175. 10.1017/S0022112000002342 |
| [20] | MURTHY M, UDAYA B K. Parametric CFD studies on hydrocyclone[J]. Powder Technology, 2012, 230: 36–47. 10.1016/j.powtec.2012.06.048 |
| [21] | 俞接成, 陈家庆, 韩景. 轴向入口油水分离水力旋流器及其数值模拟[J]. 北京石油化工学院学报, 2009, 17(2): 19–23. |
| [22] | 王丽.基于CFD的油水分离水力旋流器非尺寸因素的影响研究[D].西安:西安石油大学, 2013. |
| [23] | PANDYA D.A low cost micro scale cyclone seperator-design and computational fluid dynamics analysis[D].Arlington:the University of Texas, 2010. |




