2. 东北石油大学机械科学与工程学院
2. Machinery Science and Engineering College, Northeast Petroleum University
0 引言
随着渤海油田石油勘探开发的不断深入,计划在绥中36-1油田已有的海上平台上进行老井眼侧钻短半径水平井的技术研究,以开采周边的石油。但是高曲率的造斜井段 (井眼曲率每30m井段15°以上) 使得完井管柱串与井眼的适应性问题更加突出,如果适应性研究不清楚,会给井下管柱带来损毁失效和划出新井眼等一系列危害。适应性是指管柱通过曲率变化井段的能力,管柱下入过程中,由于井眼曲率或管柱的刚性影响,造成遇阻的现象视为不适应。在管柱可通过最大井眼曲率方面,学者们分别提出了刚性几何相容模型和弹性几何相容模型[1],并对管柱可通过最大井眼曲率进行了计算。《钻井手册 (甲方)》介绍了美国石油学会 (API) 和国际钻井承包商协会 (IADC) 推荐的套管可通过最大井眼曲率公式[2]。其中,API推荐安全系数为1.8,IADC推荐安全系数为1.20~1.25;API推荐螺纹应力集中系数为3.0,IADC推荐螺纹应力集中系数为2.0~2.5。长庆油田钻采工艺研究院与西安管材研究所联合进行了Φ139.7 mm套管的全尺寸弯曲试验;韩志勇等[3]在分析以上2种影响因素的基础上,根据试验数据并考虑轴力的影响,提出了另外一种套管可通过最大井眼曲率公式,考虑套管螺纹应力集中等因素的系数取1.65。
在摩阻力分析方面,睦满仓等[4]假定井眼轨迹曲线为一平面曲线,在井眼曲率半径较大的井中把管柱看作柔性杆,建立了水平井管柱的平面柔杆模型。于长录等[5]假设管柱是柔性的、无刚度,能传递扭矩,在管柱变形与井眼轨迹变化一致的基础之上,考虑了重力、拉力和井眼轨迹等参数的影响,建立了完井管柱三维摩阻预测数学模型,分析了水平井管柱的下入性。杜现飞等[6]采用纵横弯曲梁法和修正的软模型,对带扶正器段管柱和不带扶正器段管柱进行了摩阻分析。
在管柱可下入性分析方面,王德新等[7]建立了套管可下入性评价条件。赵域栋等[8]建立了管柱下入过程的有限元模型,运用节点迭代方法对超长细比管柱的下入过程进行了分析。陈勇等[9]将套管离散成实体单元,直井段井眼离散成刚体壳单元,建立了水平井弯曲井眼段套管下入力学模型,分析了套管在水平井中的可下入性。
笔者选取绥中36-1油田某井完井管柱为研究对象,使用弹性模型,考虑完井管柱刚度、井眼曲率、重力、扶正器和内层管柱的影响,建立完井管柱下入不同井深力学模型,利用有限元法,将管柱离散成梁单元进行模拟仿真计算,分析完井管柱与井眼曲率适应性。所得结论为绥中36-1油田后续完井管柱的现场施工提供了理论指导。
1 绥中36-1油田某井概述 1.1 作业概述绥中36-1油田位于渤海辽东湾海域,东经120°43′~121°05′,北纬39°52′~40°12′,西北距绥中市约50 km。油田范围内平均水深30 m,常年最高气温37.8 ℃,最低气温-18.0 ℃,一般年份结冰期从一月下旬至二月中旬,冰期约30 d。
1.2 完井方式根据油田油藏地质、流体特点、油藏方案、生产要求、钻井工艺,以及邻井钻完井、投产和目前生产情况,制定出的绥中36-1油田某井完井作业方式如下:
(1) 采用修井机进行作业。
(2) 工作液采用隐形酸完井液体系,水平裸眼段钻井液使用PRD体系,完井中采用与钻井液相配套的破胶液破胶。
(3) 该井设计采用Φ244.5 mm (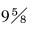
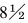
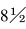
(4) 该井采用普合生产管柱,下入井下安全阀和过电缆封隔器以保证安全。
(5) 下入泵工况,监测井下压力和温度。
1.3 套管及完井管柱组成绥中36-1油田某井井身结构示意如图 1所示。

|
| 图 1 绥中36-1油田某井井身结构示意图 Fig.1 Schematic of wellbore configuration ofawellin Suizhong 36-1 oilfield |
完井管柱为双层管柱,其中外层管柱由顶部封隔器 (外径217.5 mm)、磨铣延伸筒、滑套、滑套密封筒、套管 (外径215.9 mm,长531 m)、变扣、延伸筒、防回流固井滑套、固井滑套密封筒、定位接箍、管外封隔器、密封筒、导流罩充填滑套、充填滑套密封筒、筛管 (外径215.9 mm,长279 m)、0-RING密封筒、盲管短节和浮鞋总成等部件组成,总长840 m。内层管柱由坐封工具、油管、旋转接头、冲管、滑套开关工具、滑套关闭工具、充填总成及插入密封等部件组成,总长839 m。内、外层管柱的上端通过螺纹连接,从井口到内层管柱上端连接Φ127.0 mm钻杆。
2 力学模型 2.1 基本假设下入过程中完井管柱首先在各种载荷作用下发生变形,又由于井壁的约束,管柱会和井壁发生接触,属于接触非线性力学行为。为此,笔者对完井管柱结构、外部载荷和边界条件做如下假设:
(1) 完井管柱处于线弹性范围;
(2) 不考虑管柱之间的螺纹、局部孔和槽等结构;
(3) 井壁与井眼轴线的弯曲程度一致;
(4) 完井管柱变形前轴线与井眼中心线重合;
(5) 井壁是刚性光滑的,与管柱发生接触时没有变形;
(6) 管柱自重作用力恒定,且忽略温度影响;
(7) 考虑扶正器的影响。
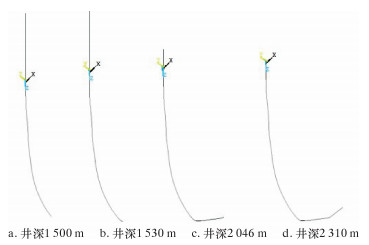
2.2 有限元模型由于管柱不可能完全刚性,使用弹性模型计算更加接近真实情况。采用有限元法,利用ANSYS软件将完井管柱离散成BEAM188单元,并选取二次形函数[10]。从完井管柱下入开窗点开始分析,建立管柱下入开窗点 (井深1 500 m)、狗腿度每30m井段10°(井深1 530~1 629 m)、狗腿度每30m井段15°(井深2 064~2 110 m) 和井底 (井深2 310 m) 等不同井深的有限元模型,如图 2所示。下放过程中,井口以上管柱全固定。
|
| 图 2 完井管柱下入不同井深有限元模型 Fig.2 Finite element model of completion string atdifferent well depths |
为模拟外层管柱与井眼的接触,在外层管柱外表面依附CONTA176接触单元,在井眼内表面依附TARGE170目标单元,创建接触对。外层管柱各部件外径不同,井眼各井段的内径也不同,存在多个环空间隙。采用增广拉格朗日乘子法接触算法,计算外层管柱与井壁之间的接触力和摩阻力。
由于内层管柱刚度较小,在下放过程中内层管柱随着外层管柱变形,内层管柱对外层管柱的影响主要考虑内层管柱的自重载荷。内、外层管柱上端通过螺纹连接,该处耦合所有自由度,其余部位耦合横向自由度,实现内层管柱自重载荷对外层管柱的作用。
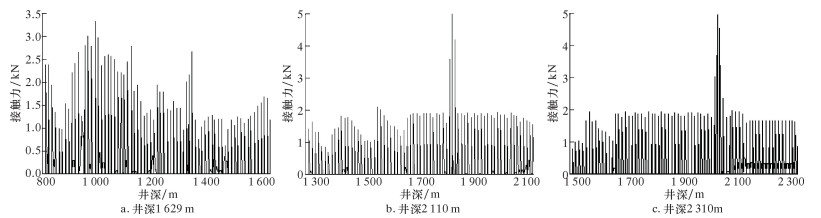
3 计算结果分析 3.1 完井管柱受力分析当下入不同井深时,其中840 m长的外层管柱的接触力曲线如图 3所示。完井管柱的轴力如图 4所示。轴力、摩阻力和受阻压力汇总结果见表 1。
|
| 图 3 完井管柱接触力随井深变化曲线 Fig.3 Thecontact force of completion string at different well depths |

|
| 图 4 完井管柱轴力随井深变化云图 Fig.4 The axial force of the completion string at different well depths |
| 下入井深/m | 井口轴力/kN | 总摩阻力/kN | 受阻压力/kN | 受阻压力对应井深/m |
| 1 500 | 482.1 | 163.7 | - | - |
| 1 530 | 468.5 | 212.9 | - | - |
| 1 629 | 505.2 | 177.7 | - | - |
| 2 064 | 489.5 | 219.4 | - | - |
| 2 100 | 481.4 | 221.1 | -0.05 | 2 096.0 |
| 2 110 | 451.8 | 304.2 | -0.20 | 2 097.3 |
| 2 200 | 505.4 | 137.4 | -1.94 | 2 103.3 |
| 2 310 | 477.0 | 185.6 | -4.86 | 2 099.4 |
由图 3可知,当下入井深为1 629 m时,由于管柱在裸眼中下入已通过每30m井段10°的高曲率井段,管柱接触力在1 530 m之后呈现增长趋势,这是裸眼井眼与原井眼相比变小和井眼曲率较大导致的。当管柱继续下入时,最大接触力出现位置也随着管柱下入而下移,这是防砂套管在这一位置分布着扶正器和封隔器等外径较大的部件导致的。在每隔12 m套管扶正器处,由于扶正器的外径比管柱本体外径大,导致每隔12 m接触力出现一个较大值。
由图 4和表 1可知,井口轴力最大,为拉力,下入不同井深井口轴力存在波动,范围在477.0~505.4 kN之间。当管柱下入井深为2 200 m时,井口轴力最大;管柱下入到井底时井口轴力最小。
当下入井深超过2 100 m之后,管柱下端存在受阻压力,范围在0.05~4.86 kN之间,下入到井底时管柱下端受阻压力达到最大,但管柱不会因受压失稳而发生屈曲。
当管柱下入井深2 110 m (井眼曲率每30m井段15°的终点) 时,总摩阻力最大,为304.2 kN,井口轴力为451.8 kN,井口轴力大于总摩阻力。
由此可见,井口轴力的变化较平缓,总摩阻力在井眼曲率较大的井段发生突变。在不同井深处,井口轴力总是大于总摩阻力,管柱不会因受压失稳而发生屈曲,能够顺利通过。
3.2 完井管柱应力分析当下入不同井深时,完井管柱应力如图 5所示。外层管柱各部件的最大应力见表 2。

|
| 图 5 完井管柱应力随井深变化曲线 Fig.5 The stress of completion string at different well depths |
| 下入井深/m | 部件名称 | 每30 m井眼 曲率/(°) |
井眼曲率引起 的应力/MPa |
等效应力有限 元解/MPa |
屈服强度552 MPa 对应的安全系数 |
屈服强度758 MPa 对应的安全系数 |
所处井深/m |
| 1 500 | 磨铣延伸筒 | 1.91 | 22.6 | 157.8 | 3.50 | 4.80 | 662.9 |
| 1 530 | 磨铣延伸筒 | 3.18 | 37.6 | 164.4 | 3.36 | 4.61 | 693.1 |
| 1 600 | 筛管 | 10.00 | 85.3 | 146.4 | 3.77 | 5.18 | 1 596.2 |
| 1 629 | 套管 | 2.51 | 21.4 | 169.0 | 3.27 | 4.49 | 1 320.1 |
| 1 900 | 变扣 | 10.00 | 96.8 | 167.2 | 3.30 | 4.53 | 1 603.0 |
| 2 064 | 浮鞋总成 | 15.00 | 141.0 | 153.8 | 3.59 | 4.93 | 2 064.6 |
| 2 100 | 筛管 | 15.00 | 128.0 | 187.7 | 2.94 | 4.04 | 2 096.2 |
| 2 110 | 筛管 | 15.00 | 128.0 | 189.7 | 2.91 | 4.00 | 2 106.3 |
| 2 310 | 筛管 | 2.00 | 17.1 | 193.5 | 2.85 | 3.92 | 2 306.2 |
由图 5可见,在狗腿度为每30m井段10°和15°的2个高曲率段应力明显变大,并且狗腿度为每30m10°井段的应力小于每30m15°井段的应力,这表明井眼曲率越大,弯曲应力也越大。每隔12 m有一个扶正器,扶正器的截面积比管柱的截面积大,因此每隔12 m管柱应力会出现一个较小值。
由表 2可知,由井眼曲率 (每30m井段15°) 引起的弯曲应力极值位于浮鞋总成部件,值为141.0 MPa。考虑接触力等载荷的影响,经有限元计算,应力为153.8 MPa,弯曲应力占等效应力的92%。
井眼曲率为每30m10°的井段,由有限元计算得到的最大应力为167.2 MPa,处于变扣位置,由井眼曲率引起的弯曲应力为96.8 MPa,占等效应力的58%。井眼曲率为每30m15°的井段,由有限元计算得到的最大应力为189.7 MPa,处于筛管位置,由井眼曲率引起的弯曲应力为128.0 MPa,占等效应力的67%。
管柱下入不同井深时,由有限元计算得到的最大应力为193.5 MPa,处于筛管位置,由井眼曲率 (每30m井段2°) 引起的弯曲应力为17.1 MPa,占等效应力的9%。
由表 2还可知,屈服强度取552 MPa时安全系数为2.85;屈服强度取758 MPa,安全系数为3.92。文献[3]推荐的安全系数为1.65,可见笔者计算的安全系数均大于推荐值,完井管柱满足强度要求。
3.3 模型验证2016年8月,中海油在塘沽钻采试验基地JJSY-4井进行固井防砂一体化完井管柱通过性试验,笔者的力学模型计算结果与现场试验符合性较好,均能顺利通过。这说明建立的模型和计算结果可指导后续的实际完井管柱施工作业。
4 结论(1) 过低井眼曲率井段时,管柱轴力、接触力和摩阻力对应力起主导作用;过高井眼曲率段时,弯曲应力对等效应力起主导作用。在井眼曲率为每30m井段10°和15°的2个高曲率井段,弯曲应力明显变大,弯曲应力占等效应力的1/2以上。完井管柱下入每30m井段10°的高曲率井段后,下端存在受阻压力,管柱不会因受压而发生屈曲变形,总摩阻小于受阻点以上管柱浮重,完井管柱本体满足强度要求。
(2) 笔者从摩阻力、稳定性和强度方面评价了完井管柱与井眼曲率的适应性,所得结果可为绥中36-1油田后续完井管柱施工提供理论指导。
| [1] | 蔡恩宏. 弯曲井段中套管通过能力分析研究[J]. 石油和化工设备, 2010, 13(8): 15–17. |
| [2] | 钻井手册 (甲方) 编写组. 钻井手册 (甲方)[M]. 北京: 石油工业出版社, 1990. |
| [3] | 韩志勇, 王德新. 套管可通过的最大井眼曲率的确定方法[J]. 石油钻探技术, 1999, 27(2): 15–17. |
| [4] | 睦满仓, 孟坤六, 杜镰. 水平井管柱下入摩阻分析及应用[J]. 石油机械, 1999, 27(2): 5–8. |
| [5] | 于长录, 金有海. 水平井完井管柱摩阻预测模型建立与下入性分析[J]. 石油机械, 2009, 37(9): 133–135. |
| [6] | 杜现飞, 王海文, 王帅, 等. 深井作业管柱下入能力研究[J]. 燕山大学学报, 2008, 32(2): 163–168. |
| [7] | 王德新, 于润桥. 套管柱在水平井弯曲段的可下入性[J]. 石油钻探技术, 1997, 25(1): 12–14. |
| [8] | 赵域栋, 狄勤丰, 王文昌, 等. 浅层水平井管柱可下入性分析及下入过程的可视化[J]. 钻采工艺, 2012, 35(3): 67–70. |
| [9] | 陈勇, 刘飞, 张兴国, 等. 水平井内套管柱下入过程的数值模拟[J]. 石油机械, 2010, 38(3): 28–30. |
| [10] | 张强, 刘巨保, 姚利明, 等. 石油钻机井架结构梁单元计算精度分析[J]. 石油机械, 2013, 41(12): 1–5. |



