2. 北京工业大学;
3. 北京信息科技大学
2. Beijing University of Technology;
3. Beijing Information Science & Technology University
0 引言
机械钻速的提高是钻井工程中永恒的目标。PDC钻头是目前主要的破岩工具之一,其利用的是岩石抗剪能力是抗压能力的1/20~1/40的性质,但是在钻遇深部硬质地层时容易出现严重的扭转振动[1-3]。PDC钻头出现严重的扭转振动时,钻头的转速波动较大,切削齿损伤严重,机械钻速低,钻井成本大幅度增加[4]。
对于PDC钻头扭转振动的原因,一部分学者认为扭转振动是由于钻头和岩石之间非线性的摩擦力造成,摩擦力的大小与两者之间的相对速度有关,相对速度越大,摩擦力越小[4-6]。然而T.RICHARD等[7]证明在钻头和岩石之间的摩擦因数为一个恒定值时,也会发生严重的钻头扭转振动,其研究指出钻头处的轴向和扭转振动存在耦合作用,轴向振动会对扭转振动产生较大的影响。为了进一步分析PDC钻头的扭转振动,需要分析轴向振动对PDC钻头扭转振动的影响。
钻井现场一般采用“低钻压、高转速”的方法来抑制扭转振动,且使用效果较为明显[8-10],但是该方法会使得机械钻速有较大的降低。一些学者开发了控制系统,通过调节转盘转速和钻压的方式来抑制扭转振动的发生,但是控制系统较为复杂,可操作性不强[11]。扭力冲击器的使用在一定的地层中能有效抑制严重的扭转振动的产生[12-13],但是该工具不能有效抑制钻压波动对PDC钻头造成的损害。
为了更好地抑制PDC钻头扭转振动的产生,笔者分析了钻压波动对钻头扭转振动的影响,并设计了抑制PDC钻头扭转振动的减振工具。
1 PDC钻头扭转振动分析 1.1 PDC钻头扭转振动模型分析钻头接在钻铤的最下端,钻铤和钻杆通过螺纹连接并向上穿过转盘处,钻杆悬挂在大钩的下端。钻进时,电机驱动转盘转动,并带动钻杆、钻铤和钻头转动来实现破碎岩石,大钩可以通过缆绳的提拉来调节钻头处所受的轴向力,即实现钻压 (WOB) 的调节。
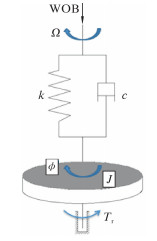
分析钻头的扭转振动时,将钻柱系统当作一个扭摆模型[5],如图 1所示。假设条件如下:①所钻的井为直井;②忽略钻柱和井壁之间的摩擦阻力;③转盘以一个恒定的转速转动并驱动钻头正向转动;④钻头没有反转[14-17]。钻压作用在钻头处,钻杆看成一个有一定扭转刚度的弹簧,钻井液对钻杆转动有一定的阻尼作用,钻头和钻铤看成一个质量集中的转动盘,钻头转动时, 岩石会产生阻力扭矩。
|
| 图 1 PDC钻头扭转振动模型 Fig.1 Torsional vibration model of PDC bit |
图 1中:Ω为转盘的转速,rad/s;k为钻杆的扭转刚度,N·m/rad;c为钻井液阻尼系数;J为转动惯量,kg·m2;Tr为阻力扭矩,N·m;Φ为钻头的转角,rad。
钻头处的扭矩平衡方程为:
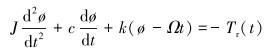
|
(1) |
当钻头处没有扭转振动时,即稳定钻进时,钻头的转速与转盘的转速相等,表达式为:
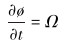
|
(2) |
当钻头处的扭矩出现波动,即Tr(t) 出现波动,钻头转动的平衡状态被打破,钻头转速开始出现波动,即钻头出现扭转振动。Tr(t) 的波动是造成扭转振动的关键原因,而Tr(t) 的值与钻头和岩石之间的相互作用有关。
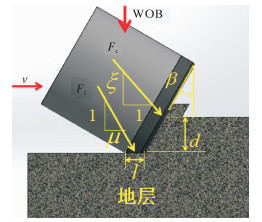
1.2 PDC钻头与岩石相互作用模型PDC钻头主要通过切削齿对岩石的切削来实现破岩。钻进过程中钻压作用在PDC钻头上,使得钻头上的PDC切削齿吃入岩石内部,转盘提供的扭矩驱动PDC钻头正向转动,切削齿对其前端的岩石进行剪切破坏。根据钻头切削齿和岩石之间的相互作用,可以将其分为切削过程和摩擦过程,其示意图如图 2所示。
|
| 图 2 PDC单个切削齿与岩石之间相互作用示意图 Fig.2 Schematic diagram of the interaction betweenasinglePDC cutter and rock |
图 2中:Fc表示作用在切削方向上的力,N;Ff表示作用在摩擦方向上的力,N;β为钻头的后倾角,rad;ξ表示切削面上钻压与扭矩之间的关系参数,与钻头的形状有关;μ为钻头切削齿和岩石之间的摩擦因数。
将扭矩和钻压分解为[7]:
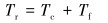
|
(3) |
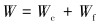
|
(4) |
其中作用于摩擦部分的压力和扭矩分别为:
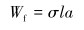
|
(5) |
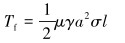
|
(6) |
式中:σ为接触应力,MPa;l为摩擦面的长度,m;a为钻头半径,m;γ的取值范围为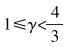
根据公式 (6) 得出摩擦部分的压力和扭矩之间的关系为:
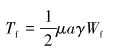
|
(7) |
切削过程中,切削扭矩和切削钻压表达式为:
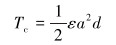
|
(8) |

|
(9) |
式中:ε为岩石硬度相关的系数,表示为单位体积的岩石被破坏所需要的能量,MPa;d为切削齿切削深度, m。
综合切削部分和摩擦部分,钻头处阻力扭矩为:
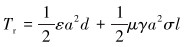
|
(10) |
由式 (10) 可知,钻头处的阻力扭矩和切削齿的切削深度呈线性关系。
根据式 (3)~式 (6) 及式 (8)、式 (9) 得出钻头切削深度和钻压之间的关系为:
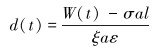
|
(11) |
由式 (11) 得出,切削深度与钻压、地层性质及钻头的特性有关,钻压的改变直接影响切削深度,影响钻头处阻力扭矩的变化。
考虑钻头处钻压波动,钻头处扭矩平衡方程为:
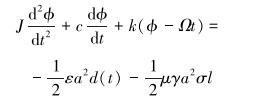
|
(12) |
实际钻进操作中,由于井下工况的复杂性,钻压波动不可避免,这就会造成钻头出现扭转振动。严重的钻压波动会造成钻头跳钻,即钻头处轴向振动的振幅较大,足以使得钻头脱离与井底的接触。跳钻是一种严重的轴向振动,会对底部钻具组合以及钻头产生很大的破坏,而实际操作中出现的情况较少,因此笔者在此没有考虑跳钻这种情况。
2 算例分析为了数学计算的方便,笔者认为钻头处的钻压处于正弦波动,即有:
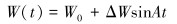
|
(13) |
计算参数如下:a=0.1 m,ε=50 MPa,σ=70 MPa,μ=0.4,c=0.03,k=700 N·m/rad,Ω=4π rad/s,l=0.001 m,ξ=0.4,J=130 kg·m2,W0=60 kN,γ=1,A=8π。
同时认为在开始时,钻头处没有扭转振动,即钻头的转速与转盘的转速相等,且加速度为0,初始条件表示为:
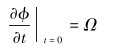
|
(14) |
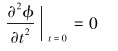
|
(15) |
对钻头的扭转平衡方程进行求解。
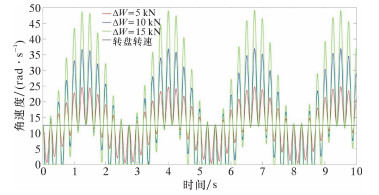
图 3为不同轴向载荷振幅时PDC钻头转速与时间的关系图。由图可知:当ΔW=5 kN时,钻头的最大转速为24.78 rad/s,最小转速为0.78 rad/s;当ΔW=10 kN时,钻头的最大转速为37.01 rad/s,最小转速为0;而当ΔW=15 kN时,钻头的最大转速为49.22 rad/s,最小转速为0。当钻头转速为0时,意味着钻头在波动范围内,会停止转动,称为黏滞状态,此时切削扭矩不足以克服阻力扭矩,但是转盘仍以一个恒定的转速转动,传递的切削扭矩不断积累在钻头处,当切削扭矩足以克服阻力扭矩时,钻头开始转动,处于滑动状态,即钻头出现黏滑振动。黏滑振动对钻头的损害极大,容易造成钻头崩齿现象[5-9],在实际钻进过程中,应尽量避免该种振动的产生。
|
| 图 3 不同轴向载荷振幅时PDC钻头转速与时间的关系 Fig.3 Relationship between PDC bit rotation speed and timeunder different axial load amplitudes |
由图 3可看出,钻压的波动直接导致钻头扭转振动的产生,并随着波动值的增大,钻头转速的波动幅值越大,即扭转振动幅值越大,振动越严重。
3 PDC钻头扭转振动减振工具设计为了保护PDC钻头,需要抑制其扭转振动,而钻头处的扭转振动可以通过平衡钻头处扭矩的方式来抑制。钻压的波动会直接造成扭矩的波动,为此可以从2个方面来进行减振:①首先是吸收部分轴向振动,降低钻头处钻压的波动;②将吸收的一部分振动能量转化为切削扭矩。基于以上分析,设计了一种抑制PDC钻头扭转振动的减振工具。
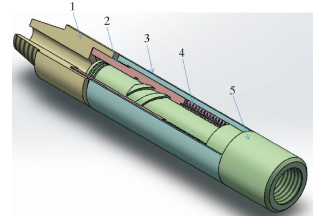
3.1 结构扭转振动减振工具的结构如图 4所示。
|
| 图 4 扭转振动减振工具结构示意图 Fig.4 Structural schematic of the damping tool 1—上部短节;2—驱动短节;3—外壳体;4—碟簧;5—钻头座。 |
上部短节和驱动短节通过端部的螺纹连接固定,外壳体和钻头座通过螺纹连接固定,驱动短节通过螺旋槽与钻头座上端外部螺旋齿相配合,其配合类似于螺纹的配合连接,驱动短节和钻头座可以围绕螺旋齿转动,在转动过程中驱动短节和钻头座的轴向位置会发生改变,进而改变碟簧的压缩量。
3.2 工作原理减振工具下端安装PDC钻头,其上端可以安装动力钻具或者钻铤。正常工作时,该工具起到一个接头的作用,即具有传递扭矩和钻压的功能。钻压通过上部短节和驱动短节来压缩碟簧并传递到钻头处。传递到该工具处的驱动扭矩通过螺旋槽和螺旋齿面之间的摩擦力来传递给钻头。
当钻压恒定时,碟簧的压缩量为恒定值。而当钻压出现波动时,驱动短节的轴向载荷出现变化,驱动短节会绕着钻头座上端的螺旋齿进行旋转,改变碟簧的压缩量。当钻压突增时,向下的轴向力使得驱动短节会向下运动,驱动钻头座沿着螺旋齿顺时针转动 (从上往下看),螺旋齿将一部分轴向力分解为切削扭矩,此时增加的轴向力分解为一部分的轴向力和一部分的切削扭矩,钻头处的扭矩得以平衡。反之,当钻压突减时,一部分的轴向力分解为反切削扭矩,且将钻头向上提拉,通过减小钻头切削齿切削深度的方式来减小阻力扭矩,使得钻头处的扭矩处于平衡状态。
常规钻进过程中,钻压的改变会改变钻头处的阻力扭矩,但是阻力扭矩的改变不会造成钻压的改变,两者之间的关系是单向的,而该减振工具将钻压和扭矩结合在一起,会根据扭矩和钻压的改变来自动调节,使其达到一个平衡状态,从而抑制钻头的扭转振动。
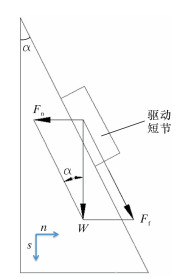
3.3 主要技术参数设计及特点图 5为PDC钻头扭转振动减振工具减振机理示意图。
|
| 图 5 PDC钻头扭转振动减振工具减振机理示意图 Fig.5 Schematic diagram of the principle of the damping tool |
图 5中:α为螺旋升角。其中,驱动短节在钻压的作用下只能沿着s方向上、下移动。由于驱动短节和钻头座之间有个螺旋齿连接,驱动短节的移动会驱动钻头座的转动,此时s方向和n方向上的力的比值为:
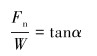
|
(16) |
螺旋升角α直接影响着轴向力和扭矩之间的转换关系,是减振工具中的关键参数。当钻头比较新时,认为轴向力的改变主要影响切削深度,影响PDC钻头切削齿前端的阻力扭矩。此时切削扭矩和轴向力之间的关系为:
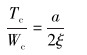
|
(17) |
螺旋升角的表达式为:

|
(18) |
根据以上分析,PDC钻头扭转振动减振工具的螺旋升角与参数成反比,参数的值越大,所需的螺旋升角越小。参数与PDC钻头切削齿的安装设置有关 (如图 2所示),尤其是切削齿的后倾角β,后倾角的值与参数ξ成正比,后倾角越小,钻头的攻击性越强,参数值ξ越小,螺旋升角的取值越大。因此后倾角的大小与螺旋升角的取值成反比。为了使得该减振工具的减振效果最佳,参数设计需要与钻头的特性相配合。
该减振工具的主要技术特点如下:①抑制PDC钻头扭转振动的发生;②将振动的能量转换为破岩的能量,增大能量利用率;③该工具长度较短,结构较简单,无电子元器件,耐温性较好;④该工具可以根据不同类型的钻头及地层需要,更换不同螺旋角的驱动短节和钻头座。
4 结论(1) 分析了轴向载荷的波动对PDC钻头扭转振动的影响。轴向载荷的波动会直接产生PDC钻头的扭转振动,轴向载荷波动值越大,产生的扭转振动的振幅越大,对钻头产生的破坏越大,当轴向载荷波动足够大时,会出现PDC钻头的黏滑振动。
(2) 为了抑制PDC钻头的扭转振动,提出并设计了扭转振动的减振工具。该工具能将波动的轴向载荷转换成一部分的切削扭矩,使得钻头处的扭矩处于平衡状态,从而抑制PDC钻头的扭转振动。工具的螺旋升角与钻头切削齿的后倾角相关,后倾角越小,螺旋升角的取值越大。
(3) 对扭转振动的减振工具进行了初步设计。研究结果对抑制PPC钻头的扭转振动提供了理论依据。
| [1] | BAILEY J J, FINNIE I. An analytical study of drillstring vibration[J]. Journal of Manufacturing Science and Engineering, 1960, 82(2): 122–127. |
| [2] | 董广建, 陈平, 邓元洲, 等. 钻柱振动与冲击抑制技术研究现状[J]. 西南石油大学学报 (自然科学版), 2016, 38(3): 121–134. |
| [3] | SPANOS P D, SENGUPTA A K, CUNNINGHAM R A, et al. Modeling of roller cone bit lift-off dynamics in rotary drilling[J]. Journal of Energy Resources Technology, 1995, 117(3): 197–207. 10.1115/1.2835341 |
| [4] | 李田军.PDC钻头破碎岩石的力学分析与机理研究[D].武汉:中国地质大学, 2012. |
| [5] | DEPOUHON A, DETOURNAY E. Instability regimes and self-excited vibrations in deep drilling systems[J]. Journal of Sound and Vibration, 2014, 333(7): 2019–2039. 10.1016/j.jsv.2013.10.005 |
| [6] | KAMEL J M, YIGIT A S. Modeling and analysis of stick-slip and bit-bounce in oil well drillstrings equipped with drag bits[J]. Journal of Sound and Vibration, 2014, 333: 6885–6899. 10.1016/j.jsv.2014.08.001 |
| [7] | RICHARD T, GERMAY C, DETOURNAY E. Self-excited stick-slip oscillations of drill bits[J]. C.R.Mecanique, 2004, 332: 619–626. 10.1016/j.crme.2004.01.016 |
| [8] | KOVALYSHEN Y. Understanding root cause of stick-slip vibrations in deep drilling with drag bits[J]. International Journal of Non-linear Mechanics, 2014, 67: 331–341. 10.1016/j.ijnonlinmec.2014.10.019 |
| [9] | GUPTA S K, WAHI P. Global axial-torsional dynamics during rotary drilling[J]. Journal of Sound and Vibration, 2016, 375: 332–352. 10.1016/j.jsv.2016.04.021 |
| [10] | NANDAKUMAR K, WIERCIGROCH M. Galerkin projections for state-dependent delay differential equations with applications to drilling[J]. Applied Mathematical Modelling, 2013, 47(4): 1705–1722. |
| [11] | PUEBLA H, ALVAREZl-RAMIREZ J. Suppression of stick-slip in drillstrings:A control approach based on modeling error compensation[J]. Journal of Sound and Vibration, 2008, 310: 881–901. 10.1016/j.jsv.2007.08.020 |
| [12] | 李玮, 何选蓬, 闫铁, 等. 近钻头扭转冲击器破岩机理及应用[J]. 石油钻采工艺, 2014, 36(5): 1–4. |
| [13] | 吕晓平, 李国兴, 王震宇, 等. 扭力冲击器在鸭深1井志留系地层的试验应用[J]. 石油钻采工艺, 2012, 34(2): 99–101. |
| [14] | ABBASSIAN F, DUNAYEVSKY V A. Application of stability approach to torsional and lateral bit dynamics[J]. SPE 30478, 1998. |
| [15] | NAVARRO-lOPEZ E M. An alternative characterization of bit-sticking phenomena in a multi-degree-of-freedom controlled drillstring[J]. Nonlinear Analysis:Real World Applications, 2009, 10: 3162–3174. 10.1016/j.nonrwa.2008.10.025 |
| [16] | ABDOLLAHI J, SKALLE P. Case study:Abnormal drillstring wash-out and fatigue experienced when drilling Hazardous formation in Iranian oil field[J]. SPE/IADC 85327, 2003. |
| [17] | JANSEN J D. Active damping of self-excited torsional vibrations in oil well drillings[J]. Journal of Sound and Vibration, 1995, 179(4): 647–668. 10.1006/jsvi.1995.0042 |



