2. 西南石油大学机电工程学院;
2. School of Mechanical Engineering, Southwest Petroleum University
0 引言
20万m3超大型非锚固立式浮顶罐(以下简称20万m3储罐)以其造价低和管理方便的优势将成为未来我国原油战略储备的主力储油设备。但是目前我国既无20万m3储罐的国家标准,也没有相关设计制造经验。伍开松等[1]对20万m3储罐的结构设计做了较为详细的工作,但是在罐-地基、液-罐作用下的地震激励动响应上仍然不明晰,尤其是三向地震激励下的屈曲失稳等问题[1-4]。
储罐的动态响应及屈曲失稳一直是国内外学者关注和研究的热点,孙建刚等[5]考虑了地基与储罐相互作用,但对于浮盘的影响未做深入研究;朱劲平和陈志平等[6-7]对地震中非锚固油罐罐内压力与液面晃动进行了较为细致的数值模拟分析;S.NATSIAVAS等[8]与M.K.SHRIMALI等[9]分析了储罐在单向地震激励下的动响应;孙颖等[10-11]分析了3类场地上无浮顶和有浮顶的有限元模型在单向地震激励下的动力响应,并对三向地震激励下的隔震与非隔震浮顶罐的动力屈曲特性进行了较为深入的研究。李扬和李自力等[12-13]运用数值方法和理论建模对隔震储罐在不同场地下的地震动响应进行了对比分析;程旭东等[14]运用ADINA软件分析了大型储罐在不同地震烈度、不同储液深度下的罐壁轴向压力,并运用JC法对罐壁抗失稳的可靠度情况进行了分析。吴灵宇[15]认为象足屈曲为罐壁纵向压力达到屈曲临界应力的屈曲破坏而非强度破坏。沈建民[16]分析了非锚固储罐的固有特性和横向激励下的动响应,并提出局部负压可能是造成菱形屈曲的原因。上述研究主要集中在15万m3以下储罐,对于20万m3及以上的储罐地震动响应与稳定性研究还未见报道。而且对于储罐的地震响应研究中,地基常常被简化为刚性体或者弹簧,对浮盘的因素也未做考虑,地震激励多采用单向激励输入载荷。
笔者以设计研究的20万m3大型非锚固原油储罐为基础,运用ADINA建立油罐-地基耦合、浮盘-罐壁耦合和罐液耦合的高度非线性模型,通过数值模拟研究了地基、浮盘对储罐动响应和稳定性的影响,重点研究了20万m3储罐三向地震激励动力响应规律及罐壁屈曲失稳。
1 流固耦合振动理论及数值建模 1.1 罐地耦合下的流固耦合动响应在G.W.HOUSNER[17]、E.ROSENBLUETH[18]和M.K.SHRIMALI[19]等人模型的基础上,在摩擦地基模型中增加弹性元件建立如图 1所示的流固耦合模型。在地震动载荷激励下,储液浮顶罐的运动控制方程为:

|
| 图 1 考虑地基的流固耦合模型 Fig.1 Fluid-structure coupling model considering foundation |
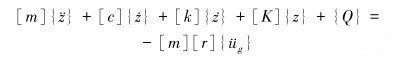
|
(1) |
式中:{z}={xc, xi, xb, yc, yi, yb}T;[m]、[c]、[k]和[K]分别为结构的质量、阻尼、摩擦因数和刚度,[m]=[mc, mi, mr]T中,mc、mi和mr分别为对流质量、冲击质量和刚体质量,流体质量与储罐之间含有接触摩擦和阻尼;{Q}={0, 0, Qx, 0, 0, Qy}T中,Qx和Qy分别是x, y方向的摩擦力矩阵;[r]是矩阵影响系数;{üg}={ügx, ügy, ügz}中,ügx、ügy和ügz分别是x, y, z方向的地震激励加速度载荷。
1.2 储罐的有限元建模根据理论模型,建立了考虑地基耦合和浮盘接触的20万m3储罐流固耦合模型,模型材料参数[19]如下:罐体密度7 850 kg/m3,弹性模量206 GPa,泊松比0.3,屈服强度490 MPa,剪切模量2.15 GPa;液体密度1 000 kg/m3,弹性模量200 MPa;地基密度1 882 kg/m3,弹性模量40 MPa。地基直径为160 m,厚度10 m;浮盘直径112 m,厚度0.22 m。储罐结构与尺寸如图 2所示。

|
| 图 2 大型储罐结构与尺寸 Fig.2 Large scale storage tank structure and size |
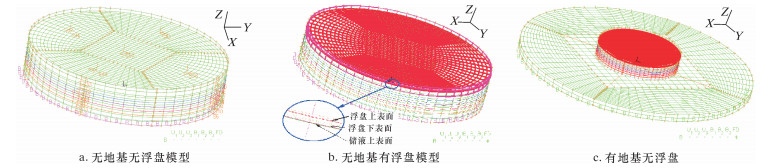
为了模拟真实工况,运用ADINA软件分别建立了无浮盘无地基、有浮盘无地基和无浮盘有地基3种模型(见图 3)。由于3种模型已能分别研究浮盘和地基的影响,故不考虑浮盘和地基同时存在的工况。
|
| 图 3 大型储罐的有限元模型 Fig.3 Finite element model of large scale storage tank |
在不影响研究目的和结果的情况下,对3种模型做了如下适当简化。
(1)油罐搁置于地基上,弹性地基与油罐底部采用接触耦合,摩擦因数设置为0.3。
(2)罐体采用理想弹塑性材料。
(3)储罐内的流体采用水作为试压介质,有限元模型采用的势流体单元,该单元是基于G.W.HOUSNER[17]提出的质量-弹簧系统模型。
(4)浮盘与罐壁之间考虑接触。在不影响模型整体分析结果的前提下,忽略加强圈、边缘板和其他附件。储罐8层罐壁和罐底采用了9种不同壳单元,分别定义其厚度与强度参数。
(5)地震激励波采用EI波,峰值加速度在南北向为0.4g,地震烈度为9度, 地震三向加速度谱采用前30 s波形(见图 4)。由于大多数文献采用的仅为水平激励地震波,为了更为全面地研究地震激励波的影响,分别采用南北单向地震激励、南北和东西两向地震激励(后文简称“两向地震激励”)以及三向地震激励进行研究。

|
| 图 4 三向地震波加速度时程曲线 Fig.4 Time-history curve of three-direction seismic wave acceleration |
2 储罐的晃液规律研究
由于20万m3大型储罐目前还没有相应的国际标准,国内也缺乏设计及建造经验,而储罐的晃液波高、罐壁内侧动压力和应力等是储罐设计标准的重要指标,在目前没有试验条件下数值仿真方法是替代试验的最佳选择。
2.1 晃液波高分析油罐设计标准中,固定顶和浮顶油罐的最高设计液位与罐壁上沿的距离应当大于储罐液面的晃动波高[7],因此有必要研究20万m3原油储罐在地震下的晃液规律。不同地震波组合下液面节点的波高时程曲线如图 5所示。由图可以看出,单向的地震激励使得晃液在后期显著偏大,多向地震激励使波高波动发散且不规律。现有资料都认为浮盘能够显著抑制液面的晃动,针对20万m3储罐,有浮盘模型的晃液波高幅值比无浮盘模型降低约50%(如图 6中第25 s时刻);图中有地基模型与无地基模型的波高幅值相近,但是波高幅值变化的波动性较大。

|
| 图 5 不同地震波组合下液面节点的波高时程图 Fig.5 Wave height time history of liquid level nodes under different combinations of seismic waves |

|
| 图 6 不同模型下的液面波高时程图 Fig.6 Wave height time history of liquid level ofdifferent models |
分别取地基模型液面R=54.1、50.4和46.7 m的环向节点,结果显示晃动波高呈余弦函数分布。在不同时刻、不同的环向路径幅值, 频率是不一样的,即越靠近罐壁边缘,三角函数的幅值A越大,不同时间三角函数的相位φ也不一样,如图 7所示。

|
| 图 7 16.4 s环向节点波高 Fig.7 Wave height of peripheral node at 16.4 s |
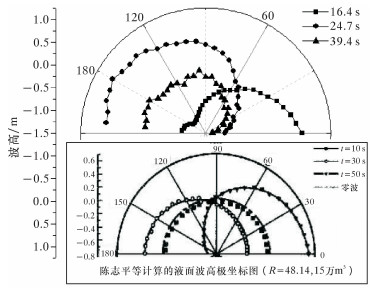
陈志平等[7]采用单向地震激励和刚性地基约束,对比发现两者有明显差别(见图 8)。
|
| 图 8 R=50.4 m不同时刻波高 Fig.8 Wave height in different time at R=50.4 m |
20万m3储罐液面环向节点的波高不是严格的三角函数,而是具有明显的随机扰动特性,这表明多向地震波与地基弹性对波高有较大影响。
2.2 罐壁动压力分析采用三向地震激励下的有地基罐模型,从罐壁正北端开始(南北方向为地震激励最大方向),每隔30°选取罐壁0~20.18 m轴向方向一组节点进行动压力分析(见图 9)。由图可以看出,储罐的动压力呈现抛物线函数。在地震最大激励来源方向夹角中,北偏0°、北偏90°和北偏180°是动压力最大的部位。储罐在上端的动压力在各个方向上是差别最大的,这是上端晃液剧烈导致。进一步对比分析结果如图 10所示。由图可以看出,地基会使储罐上、下部的动压力偏大,浮盘和地基会使罐壁动压力呈现不规律的抛物线形,并且储罐中部动压力明显增大许多,可见不考虑地基和浮盘的模型偏于保守。

|
| 图 9 罐壁不同震源夹角的动压力 Fig.9 Dynamic pressure distribution on tank wall withdifferent seismic source angles |

|
| 图 10 3种模型罐壁高度方向动压力 Fig.10 Dynamic pressure distribution along the heightof tank at three different models |
3 屈曲失稳研究
储罐象足屈曲是大型储罐独有的失效形式[14-15],储罐的设计和分析对这一问题都是十分重视。20万m3原油储罐属于短圆柱压力容器,由于结构庞大、储液多及地基范围大,影响失稳的因素与小容量储罐又存在区别。动压力是影响大型储罐屈曲的关键因素[14-17],但是动压力的形成却是外部地震激励产生因素(地震激励),屈曲最初是压力容器的局部扰动导致[20]。因此,研究外部激励与储罐局部失稳对认识20万m3储罐的象足屈曲形成机理十分重要。
对地基模施加三向地震激励,并在局部施加微小扰动,模拟得到了20万m3储罐的象足屈曲现象,如图 11所示,仿真结果与A.El-ZEINY提供的现场图片一致[21]。对比现场图和仿真结果发现:象足屈曲发生部位存在于罐壁第1圈(即0~2.981 m),发生范围也只有40°左右,而不是整个罐壁下部。

|
| 图 11 象足屈曲与仿真结果 Fig.11 Elephant foot buckling and the results of simulation |
3.1 地震激励影响
实践证明,储罐在不同地震激励下具有不同的动响应,因此罐壁稳定性与地震激励之间存在密切的关系。分别选取载荷步0.02 s的TALF波、载荷步0.02 s的EI波和载荷步0.10 s的EI波(见图 12a),分析发现载荷步时间间隔越小储罐越早接近屈服应力;TALF波和EI波导致的失稳时间差异较大。

|
| 图 12 不同地震激励波下节点有效应力时程图 Fig.12 Effective stress time history curve of nodes under different seismic excitation waves |
上、下地震激励是储罐屈曲失稳的原因之一,提取有地基模型罐壁2.98 m处节点的有效应力时程曲线(见图 12b),节点有效应力最大值发生在第4.0 s和第39.5 s 2个时刻,分别为3.57×105 Pa (两向地震波)和3.87×105 Pa (三向地震波)。第4.0 s时水平地震激励加速度最大,此时的应力极值由加速度引起;而第39.5 s时,由于存在上、下地震激励,能量在储罐中不断累积,导致有效应力极值出现在储罐罐壁;并且在地震后期可以看见,存在上、下地震激励的三向地震激励容易使应力极值震荡,这易导致储罐的浮盘边缘、中上部和下部3处失效。
为了了解地震激励后期应力极值出现时的罐壁轴向受力情况,取第39.5 s时罐壁正北端轴向节点的有效应力(见图 13)。有上、下方向地震激励下,总压力将增加50%左右,尤其是罐壁下方总压力更大。

|
| 图 13 不同方向地震波组合总压力与有效应力沿高度方向的变化 Fig.13 Total pressure and effective stress along height of tank under different direction seismic combinations |
分析结果表明:当只考虑南北单向波激励下,罐壁最大有效应力发生在储罐2.98~5.96 m处(第2圈罐壁),也是象足屈曲发生的部位。而考虑三向地震波时,最大有效应力发生14.00~16.68 m处(第6圈罐壁),该部位是菱形屈曲发生的部位(见图 13b)。可见不同的地震激励方式将导致不同的储罐屈曲失稳部位,设计建造储罐时应当根据本地区地震不同激励方式予以关注。
3.2 罐壁局部初始扰动的影响压力容器设计认为当压力容器外压逐渐增加到某一临界值,壳体不论什么原因以微小的侧向扰动,即可使壳体产生突然屈曲[20]。原油储罐屈曲2个主要因素之一是罐壁承受轴向载荷,微小挠度导致储罐在地震轴向载荷下极易发生屈曲失稳。
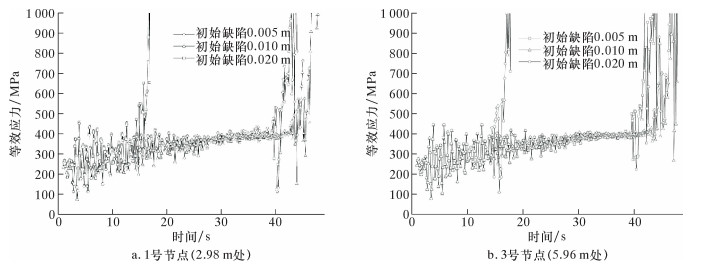
通过ADINA软件中的重启动技术,将储罐罐壁2.98 m处1号节点分别向径向移动0.005、0.010和0.020 m作为储罐的初始扰动。图 14a显示储罐罐壁上2.98 m处失稳的时间分别为43.6、40.0和15.0 s,局部初始扰动超过某一范围时,初始扰动值越大,储罐发生屈曲失稳的时间越早。为验证这一结论,同时取南北夹角30°方向罐壁5.96 m处的3号节点作为对比(见图 14b),其结果基本一致。
|
| 图 14 节点等效应力时程图 Fig.14 Time-history curve of equivalent stress of nodes |
由于地震最大激励载荷的来源方向是在南北向,在初始扰动下,储罐屈曲部位与震源方向的角度也是设计和建造中的重点。分别取初始扰动0.005和0.020 m 2种工况分析第1圈罐壁有效应力(见图 15)。分析结果表明:在三向地震激励下有效应力变化最大的3个区域分别为15°~30°、70°~80°和160°~170°。这3个方位实际上与EI人工波南北向和东西向合成加速度极值方向较为一致。这说明储罐的屈曲破坏与地震来源方向有一定关系,如果在设计建造时能够加强这些部位的抗震性能,将大大降低地震造成的损害。

|
| 图 15 含有不同初始缺陷屈服前、后有效应力变化 Fig.15 Effective stress of tank with different initial defects before and after yielding |
4 结论
(1)地震激励下,浮盘可有效降低波高,地基对波高影响不大;储罐的液面晃液波高呈余弦函数,多向地震激励比单向激励产生波高更加不规律,靠近罐壁的波高更大。
(2)储罐罐壁上的动压力呈现抛物线函数,浮盘和地基会使罐壁动压力呈现不规律的抛物线形。地震最大震源方向北偏0°、北偏90°和北偏180°是动压力最大的角度,储罐中上部动压力是轴向最大的部位。
(3)在三向激励和初始扰动下模拟得到了储罐的象足屈曲现象,模拟结果与实际案例吻合。分析表明高频的地震激励和有上、下地震激励情况下,储罐更容易发生屈曲失稳,设计建造中应当注意这一点。
(4)分析不同初始扰动下的罐壁稳定性,发现较大初始扰动会导致储罐提前屈曲失稳,最大地震激励源方向和初始缺陷都会影响储罐的稳定性。
| [1] | 伍开松, 蔡灿, 吴霁薇, 等. 20万m3原油储罐的关键结构参数设计与优化分析[J]. 机械科学与技术, 2013, 32(11): 1604–1609. |
| [2] | 岳宝增, 祝乐梅, 于丹. 储液罐动力学与控制研究进展[J]. 力学进展, 2011, 41(1): 79–92. |
| [3] | 沈利英, 沈士明. 大型储罐地震动力响应研究综述[J]. 压力容器, 2008, 25(9): 49–53. |
| [4] | 张瑞甫, 翁大根, 倪伟波, 等. 特大型LNG储罐抗(减)震研究发展综述[J]. 结构工程师, 2010, 26(5): 164–171. |
| [5] | 孙建刚, 宫克勤, 齐含兵, 等. 水平地震作用下无锚固储罐应力与应变响应分析[J]. 地震工程与工程振动, 2007, 27(3): 110–115. |
| [6] | 朱劲平, 陈志平, 蒋家羚.地震中非锚固油罐罐内压力及液面晃动的数值模拟[C]//第十届全国高等学校过程装备与控制工程专业教学改革与学科建设成果校际交流会论文集.北京:化学工业出版社, 2006:351-355. |
| [7] | 陈志平.大型非锚固储罐应力分析与抗震研究[D].杭州:浙江大学, 2006. http://cn.bing.com/academic/profile?id=2691768068&encoded=0&v=paper_preview&mkt=zh-cn |
| [8] | NATSIAVAS S, BABCOCK C D. Buckling at the top of a fluid filled tank during base excitation[J]. ASME Journal of Pressure Vessel Technology, 1987, 109(4): 374–380. 10.1115/1.3264919 |
| [9] | SHRIMALI M K., JANGID R S.. Earthquake response of liquid storage tanks with sliding systems[J]. JSEE:Summer and Fall, 2002, 4(2/3): 51–61. |
| [10] | 孙颖, 孙建刚, 崔立富, 等. 浮顶储罐在地震载荷作用下数值模拟分析[J]. 科学技术与工程, 2011, 11(19): 4657–4659. |
| [11] | 孙颖, 崔利富, 孙建刚, 等. 三向地震激励下浮顶储罐动力屈曲[J]. 大连海事大学学报, 2012, 38(3): 121–125. |
| [12] | 李扬, 李自力, 张艳. 不同类型场地对隔震储罐地震响应的影响[J]. 中国石油大学学报(自然科学版), 2008, 32(5): 108–113. |
| [13] | 李自力, 李扬, 李洪波. 大型LRB隔震储罐地震反应参数研究[J]. 四川大学学报(工程科学版), 2010, 42(5): 134–141. |
| [14] | 程旭东, 胡晶晶, 徐剑. 大型储罐地震作用下罐壁抗失稳可靠度分析[J]. 中国石油大学学报(自然科学版), 2011, 35(3): 140–143. |
| [15] | 吴灵宇.考虑液体晃动和罐底提离的立式储罐地震反应分析[D].哈尔滨:哈尔滨工业大学, 2005. http://www.cnki.com.cn/Article/CJFDTotal-HEBX200702001.htm |
| [16] | 沈建民.大型油罐的静强度及动力响应分析[D].杭州:浙江大学, 2006. |
| [17] | HOUSNER G W. The dynamic behaviour of water tanks[J]. Bulletin of the Seismological Society of America, 1963, 53(2): 381–387. |
| [18] | ROSENBLUETH E, NEWMARK N M. Fundamentals of earthquake engineering[M]. Englewood Cliffs, NJ: Prentice Hall, 1971 . |
| [19] | SHRIMALI M K., JANGID R S.. Seismic response of liquid storage tanks isolated by sliding bearings[J]. Engineering Structures, 2002, 24(7): 909–921. 10.1016/S0141-0296(02)00009-3 |
| [20] | 王文志, 蔡良仁. 化工容器设计[M]. 北京: 化学工业出版社, 2009 : 148 -151. |
| [21] | El-ZEINY A.Nonlinear time-dependent seismic response of unanchored liquid storage Tank[D].California:University of California, 2000. |



