2. 广西南宁市北部湾航空有限公司;;
3. 辽河油田塔里木项目部;;
4. 中原石油工程公司;;
5. 辽河油田欢喜岭采油厂采油作业三区;
2. Guangxi Beibu Gulf Airlines ;
3. Tarim Project Department of Liaohe Oilfield ;
4. Zhongyuan Petroleum Engineering Company ;
5. Huanxiling Oil Production Plant of Liaohe Oilfield
0 引言
弯壳体螺杆钻具是定向井和水平井施工的关键工具,其造斜率是否满足钻井设计要求是定向井和水平井轨迹控制成败的关键[1]。弯壳体螺杆钻具最早于1985年由H.KARISSON等人开始研究,并提出了3点定圆法;1990年,R.STUDER等[2]提出了双半径法;2004年,刘修缮提出了3点定圆的改进方法,首次考虑结构弯角位置对导向钻具造斜率的影响。
笔者在上述研究成果的基础上,基于最小势能原理,对螺杆钻具几何造斜率进行了研究。钻具组合达到稳定的力学平衡状态时,钻头的侧向力会趋于0,此时钻具组合的几何形状决定了工具最大的造斜率(极限造斜率)。准确地设计螺杆钻具的造斜率是实现滑动导向钻井的关键技术。笔者考虑下稳定器与井壁的间隙对双弯壳体钻具几何造斜率的影响,定义了间隙影响产生的附加造斜率,改进了几何造斜率计算公式,并用改进公式分析了影响造斜率的几个因素,所得结果符合现场实际,可为螺杆钻具的现场应用提供指导。
1 螺杆钻具几何造斜率的计算由于底部钻具组合与井壁的接触情况不规则,扶正器与井壁的接触点动态变化,所以圆上的点通常在扶正器和钻头的中心线上[3]。现场常常使用欠尺寸的扶正器[4],即扶正器与井眼之间存在间隙,这会对螺杆钻具的造斜率产生较大影响。因此,必须考虑间隙对螺杆钻具造斜率的影响。造斜率计算公式为:
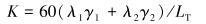
|
(1) |
式中:K为双弯螺杆钻具产生的造斜率,(°);λ1为下弯角位置影响因子,λ1=(L3+L4)/LS; LS为两扶正器间的长度,LS=L2+L3+L4,m;λ2为上弯角位置影响因子,λ2=4/LS; γ1为双弯螺杆钻具的下结构弯角,(°);γ2为双弯螺杆钻具的上结构弯角,(°);LT为造斜钻具总长度,LT=L1+LS,m。
文献[5]考虑间隙对造斜率影响的公式为:
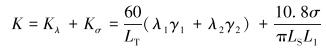
|
(2) |
式中:σ为下稳定器与井眼间隙,mm;Kλ为弯角产生的造斜率,(°);Kσ为间隙影响产生的附加造斜率,(°)。
式(2)以其计算简单而被广泛应用,但是有2个缺点:①仅考虑了2扶正器间钻具的长度LS,不够全面,应以造斜钻具总长度LT来代替,以下会给出证明;②当间隙σ增大时,式(2)计算得出的造斜率K随之增大,与现场实际不符。文献[4]准确指出,下稳定器磨损即间隙变大,会造成极限曲率减小。另外,在相关的导向螺杆钻具使用说明书中也查到,弯壳体螺杆钻具添加垫块(减小间隙)有助于提高造斜率。因此,采用式(2)计算的极限造斜率不够准确,有必要进行改进。
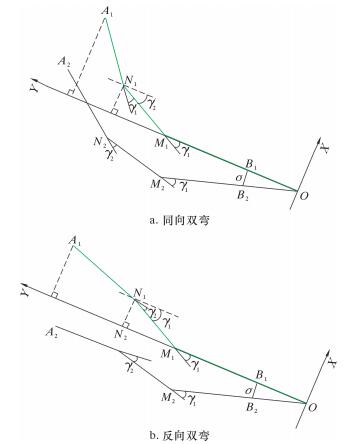
2 间隙对造斜率影响公式的改进依据最小势能原理[6],下入井中的螺杆钻具由于刚度大,不会发生形变。在双弯螺杆钻具上加入近扶正器与井眼的间隙,黑色线表示受间隙影响的螺杆钻具位置,如图 1所示。
|
| 图 1 双弯螺杆钻具简化示意图 Fig.1 Simplified schematic diagram of double tilt positive displacement motor |
C点表示钻头中心点,相当于第1点;Bi(B1和B2,以下类似)表示下稳定器的中心点,相当于第2点; Mi表示双弯螺杆钻具的下弯点;Ni表示双弯螺杆钻具的上弯点;Ai表示远离钻头扶正器的中心点,相当于第3点。σ表示B1、B2间的距离,β表示间隙引起的偏移角。定义间隙影响产生的附加造斜率Kσ等于间隙影响产生的偏移角度β与3点定圆弧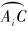
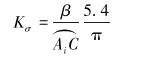
|
(3) |
针对中长半径水平井,造斜半径R一般超过100 m,故造斜钻具总长度LT«R。因此有β=σ/L1,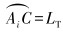
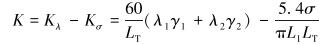
|
(4) |
保持L1=1.15 m、L2=0.81 m、L3=4.27 m、L4=1.20 m、σ=2 mm不变,由程序计算得出γ2与γ1不同组合下钻具的造斜率,结果如表 1和表 2所示。
| γ1/(°) | γ2=1.50° | γ2=1.25° | γ2=1.00° | γ2=0.75° | γ2=0.50° |
| 1.75 | 14.22 | 13.84 | 13.45 | 13.06 | 12.78 |
| 1.50 | - | 12.08 | 11.69 | 11.30 | 10.92 |
| 1.25 | - | - | 9.93 | 9.55 | 9.16 |
| 1.00 | - | - | - | 7.79 | 7.40 |
| 0.75 | - | - | - | - | 5.64 |
| γ11/(°) | γ2=-1.50° | γ2=-1.25° | γ2=-1.00° | γ2=-0.75° | γ2=-0.50° |
| 1.75 | 9.59 | 9.98 | 10.36 | 10.75 | 11.13 |
| 1.50 | - | 8.22 | 8.60 | 8.99 | 9.38 |
| 1.25 | - | - | 6.85 | 7.23 | 7.62 |
| 1.00 | - | - | - | 5.47 | 5.86 |
| 0.75 | - | - | - | - | 4.10 |
对表 1中的数据分析可得以下结果:①同行比较,上弯角γ2以0.25°差值递减,每30 m造斜率以0.38°的差值递减;②同列比较,下弯角γ1以0.25°差值递减,每30 m造斜率以1.76°的差值递减;③γ1与γ2差值为0.25°(0.50°、0.75°和1.00°)时,随着弯角的减小,每30 m造斜率均以2.15°的差值递减。
对表 2中的数据分析可得以下结果:①同行比较,上弯角γ2以0.25°差值递增,每30 m造斜率以0.38°的差值递增;②同列比较,下弯角γ1以0.25°差值递减,每30 m造斜率以1.76°的差值递减;③γ1+γ2=0.25°(0.50°、0.75°和1.00°)时,随着弯角γ1的减小,每30 m造斜率均以1.37°的差值递减。
(1)通过①和②结果比较,下弯角γ1对造斜率的影响是上弯角γ2的4.6倍。因此,下弯角对造斜率的影响非常显著,符合现场实际。
(2)通过对③结果的分析得出,造斜工具2个弯角的差值对造斜率的递减值并没有影响,这可以用来快速求得任意2个结构弯角组合的螺杆钻具的造斜率。
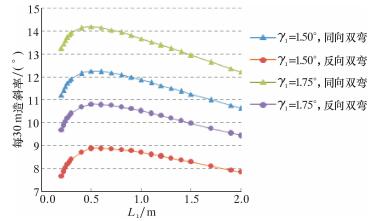
3.2 下稳定器至钻头的距离L1对造斜率的影响采用控制变量法,保持L2=0.81 m、L3=4.27 m、L4=1.20 m、γ1=1.50°(γ1=1.75°)、γ2=±1.00°、σ=2 mm不变,考虑间隙情况下,绘出双弯螺杆钻具造斜率K与L1的关系曲线,如图 2所示。图中L1的范围参考了胜利油田水平井所用的下稳定器距钻头的范围[8-11],并在此基础上适当放宽范围,使L1,取值在0.2~2.0 m之间。
|
| 图 2 造斜率K与L1的关系曲线 Fig.2 Curve of the relationship betweenbuild-up rate K and L1. |
由图 2可知:①在L1 < 0.5 m时,双弯螺杆钻具的造斜率K随着L1的增加急剧增大;当L1>0.5 m时,双弯螺杆钻具的造斜率K随着L1的增加缓缓减小。②无论是同向双弯还是反向双弯,曲线都有对应的最优造斜率,2个最优造斜率对应的L1=0.5 m。因此,在考虑间隙影响的情况下,理论上L1应选择在0.5 m左右。但是,钻头与下扶正器之间一般放有测斜仪器,故在现场L1一般选择在1.0~1.5 m之间。
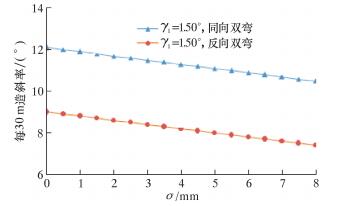
3.3 下稳定器与井壁的间隙σ对造斜率的影响保持L1=1.15 m、L2=0.81 m、L3=4.27 m、L4=1.20 m、γ1=1.5°、γ2=±1°不变,考虑间隙的情况下,绘出双弯螺杆钻具的造斜率K与σ的关系曲线,如图 3所示。图中,σ的范围是0.5~8.0 mm。
|
| 图 3 造斜率K与σ的关系曲线 Fig.3 Curve of the relationship betweenbuild-up rate K and σ |
由图 3可知,对于同向和反向双弯螺杆造斜工具,当下稳定器与井壁的间隙σ增加时,造斜率K都呈线性减小,这与现场实际情况相符合。在造斜时为了保证造斜率不发生变化,必须采用高耐磨材质的下稳定器,减少下稳定器的磨损。反之,也可采用易磨损材质的扶正器来增大间隙,减小工具造斜率。
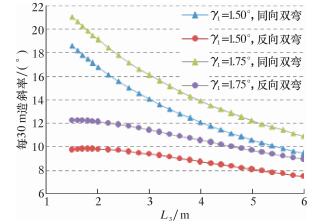
3.4 两弯角之间的距离L3对造斜率的影响采用控制变量法,保持L1=1.15 m、L2=0.81 m、L4=1.20 m、γ1=1.50°(γ1=1.75°)、γ2=±1.00°、σ=2 mm不变[9],考虑间隙情况下,绘出双弯螺杆钻具的造斜率K与L3的关系曲线,如图 4所示。图中L3的取值范围是1.5~6.0 m[10]。计算得出在K=19°时,螺杆钻具的最大长度(LT)max=5.70 m,而LT=4.61 m;在K=8°时,(LT)max=8.77 m,而LT=8.36 m。因此,设计的螺杆钻具能顺利下入井中。
|
| 图 4 造斜率K与L3的关系曲线 Fig.4 Curve of the relationship betweenbuild-up rate K and L3 |
由图 4可知:①对于反向双弯螺杆钻具,两弯角间的距离L3=2 m时有较高的造斜率;当L3 >2 m时,其造斜率近似呈线性减小。②对于同向双弯螺杆钻具,造斜率K随着L3的增加而减小。通过曲线拟合,满足对数函数K=AlnL3+B关系式,相关系数均为0.999,其中A、B均为参数。
4 现场实例计算实例一采用辽河油田静33-侧平71套管侧钻水平井数据,采用的螺杆钻具型号为5LZ95×7Y7。给出螺杆钻具基本参数:L1=1.13 m、L2=0.13 m、L3=2.80 m、L4=0.30 m、γ1=3.0°、γ2=1.8°,控制钻压在50~70 kN,间隙σ=2 mm。计算的每30 m造斜率如表 3所示。
实例二采用辽河油田静59侧钻水平井数据,采用的螺杆钻具型号为5LZ95×7.0。给出螺杆钻具基本参数:L1=0.77 m、L2=0.13 m、L3=2.60 m、L4=0.30 m、γ1=1.0°、γ2=1.0°,控制钻压在2~3 kN,间隙σ=4 mm。计算的每30 m造斜率见表 4。
通过以上2则实例验证得出,经过笔者改进的造斜率计算公式其精度比文献[4]的精度高,误差小。这说明改进的造斜率计算公式更加符合现场实际。
5 结论(1)在钻井导向工具的设计中,造斜率是主要的参考依据。笔者在借用修正3点定圆原理的基础上,改进了扶正器与井眼间隙对造斜率影响的计算公式,考虑了间隙产生的附加造斜率与偏移角度的关系,提高了计算精度,通过实例验证符合现场实际。
(2)在改进公式计算的基础上,对螺杆钻具的结构弯角、下稳定器至钻头的距离、下稳定器与井壁的间隙及两弯角之间距离的敏感性做了相应分析,得出了相应的有实质性的结论,所得结论可对螺杆钻具的现场应用提供指导。
| [1] | MURPHEY C E. Hole deviation and drill string behavior[J]. Society Petrdeum Engineers Journal, 1966, 6(1): 44–54. 10.2118/1259-PA |
| [2] | STULERT R, SIMON C, GENEVOIS J M, et al.Learning curve benefits resulting from the use of a unique BHA directional behavior drilling performances post-analysis[R].SPE 110432, 2007. |
| [3] | 刘修善. 导向钻具几何造斜率的实用计算方法[J]. 天然气工业, 2005, 25(11): 50–52. |
| [4] | 刘修善, 王成萍, 程安林. 弯壳体导向钻具的设计方法[J]. 石油钻采工艺, 2005, 27(4): 18–23. |
| [5] | 唐雪平, 陈祖锡, 汪光太, 等. 中短半径水平井弯壳螺杆钻具造斜率预测方法研究[J]. 钻采工艺, 2000, 23(3): 13–18. |
| [6] | 刘修善, 何树山, 邹野. 导向钻具几何造斜率的研究[J]. 石油学报, 2004, 25(6): 83–87. |
| [7] | WARREN T M. Steerable motors hold their own against rotary steerable systems[R].SPE 104268, 2006. https://www.researchgate.net/publication/254525777_Steerable_Motors_Hold_Their_Own_Against_Rotary_Steerable_Systems |
| [8] | 苏义脑. 螺杆钻具研究及应用[M]. 北京: 石油工业出版社, 2001 : 205 -208. |
| [9] | 王宝新, 许岱文, 程存志. 弯壳动力钻具造斜率的几何分析与计算[J]. 石油钻采工艺, 1994, 16(1): 32–37. |
| [10] | KARISSON H, BRASSFIELD T, KRUGER V.Performance drilling optimization[R].SPE 13474, 1985. |
| [11] | 石晓兵, 李黔, 施太和, 等. 双弯螺杆降斜时的钻柱强度分析[J]. 石油钻采工艺, 2001, 23(4): 7–9. |




