2. 西南石油大学石油工程学院;
2. College of Petroleum Engineering, Southwest Petroleum University
0 引言
近年来,随着冀东油田勘探开发力度的加大,复杂井钻探工作量呈逐年上升的趋势,钻具失效事故率也随之增加。钻具失效会导致钻井周期延长、钻井成本增加,甚至导致填眼侧钻,造成巨大的经济损失[1-10]。
通过对近几年冀东油田钻具失效事故进行分析,发现钻具失效事故发生井段多为“S”形井上部井段“狗腿”(井眼曲率)较大处。前期在“S”形井和大斜度井等复杂轨迹井眼钻具设计时,绝大部分只考虑钻具所受的扭矩、起下的拉伸载荷以及是否发生屈曲变形,而关于井眼弯曲处对钻具应力的影响没有充分考虑。实践证明,在“S”形复杂轨迹井眼中,井眼弯曲会对钻具产生疲劳破坏,从而严重影响钻具寿命,是钻具设计中不可忽略的要素。鉴于此,笔者对“S”形井眼钻具组合进行力学分析,并计算井眼曲率限制下的最大轴向拉力及复合应力下钻具的疲劳系数,对钻压、钻具刚性及钻具组合等进行优化和调整,这样可预先将疲劳系数控制在合理范围,从而大幅降低钻具失效事故率。
1 钻具失效力学分析若井眼曲率较大,则钻具受到的弯曲应力较大,同时也受下部钻具重力引起的轴向拉力;在大斜度井中,钻具还受到较大的扭矩产生的剪应力。其中钻具所受的弯曲应力越大,就越容易产生疲劳破坏而导致失效。因此,笔者提出疲劳系数的概念,即钻具所受的弯曲应力与最大允许弯曲应力的比值。当疲劳系数大于1时,钻具发生疲劳破坏的可能性大大增加。
1.1 井眼曲率限制下的最大轴向拉力Lubinski研究指出,当钻杆在井眼曲率渐变的井眼中旋转时,弯曲应力与井眼曲率及钻杆所受的轴向力有关。
假设在井眼曲率较大井段只讨论2个钻杆接头之间的钻杆,其自身重力与所承受的纵向拉力(或压力)相比可以略去不计,另外在承受拉力时,钻杆轴线是一个平面弹性曲线[2-3]。
钻杆在弯曲井眼中的受力分析如图 1所示。图中OA表示钻杆轴线的一部分,坐标原点为O,X轴在O处与管轴线相切。设T为拉力,So为O点的剪力,Mo是O点的内力矩,在OA的端点处设钻杆的内力矩为M,则有:
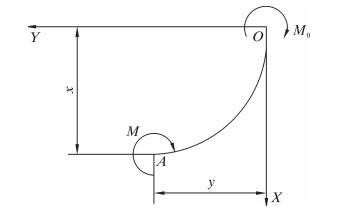
|
| 图 1 钻杆在弯曲井眼中的受力分析 Fig.1 Force analysis of drill pipe in curved borehole |
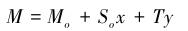
|
(1) |
由材料力学可知,O点的力矩与该点的曲率Co的关系为:
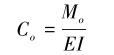
|
(2) |
式中:E为弹性模量,Pa;I为截面惯性矩,m4。
承受弯矩梁的线弹性微分方程为:
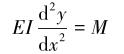
|
(3) |
由式(1)、式(2)和式(3)可得:
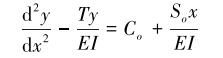
|
(4) |
微分方程(4)满足O点的边界条件的解为:
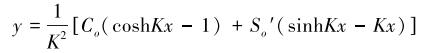
|
(5) |
式中:
假设钻杆在渐变的井眼曲率上受拉力,如图 2所示。
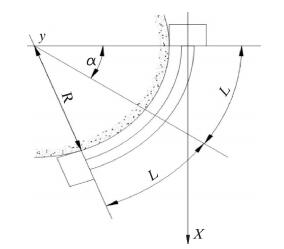
|
| 图 2 弯曲钻杆与井眼曲率之间的几何关系 Fig.2 Geometrical relationship between the curved drill pipe and borehole curvature |
由材料力学可知,受弯矩Mo作用的梁,其弯曲应力为:
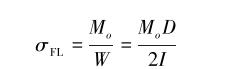
|
(6) |
将式(6)带入式(2)可得:
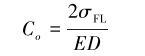
|
(7) |
式中:D为钻杆外径, mm;σFL为通过古德曼曲线求得的钻具最大允许弯曲应力,MPa。
设2L代表钻杆2接头之间的长度,由于对称,所以x=L处的管子变形弹性线与井眼轴线平行。设α表示L长度内的井眼偏斜角,R代表曲率半径,则L=Rα[2-3]。
令C代表井眼曲率,则有C=1/R,α=LCo,中点的边界条件
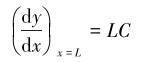
|
(8) |
对式(5)求导可得:
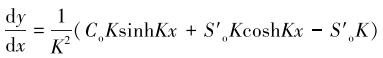
|
(9) |
将式(9)带入式(8)可得:
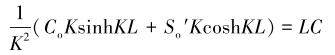
|
(10) |
对式(5)3次求导得:
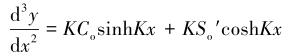
|
(11) |
将式(11)分别带入式(8)和式(10)并化简,得:
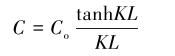
|
(12) |
式中:C为边界条件下允许的每30 m最大井眼曲率,(°)。
将式(7)带入式(12)并化简得:
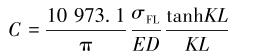
|
(13) |
式中:L为钻杆接头之间长度的½,m;L=4.572 m;I为钻杆的惯性矩,
最大允许弯曲应力可以通过古德曼公式求得:
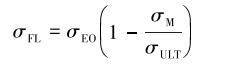
|
(14) |
式中:σEO为钻杆耐受极限,MPa;σM为井眼曲率下部钻杆产生的轴向应力,MPa;σULT为钻杆抗拉强度,MPa。
轴向应力计算式为:
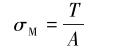
|
(15) |
式中:A为钻杆横截面积,m2。
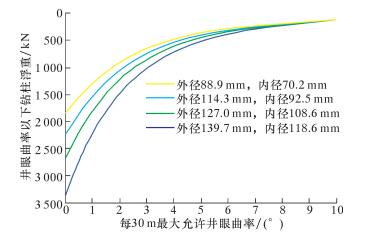
现场常用钻杆为G105钻杆,通过式(13)计算得到不同规格钻杆在不同井眼曲率下部钻具轴向拉力(浮重),结果如图 3所示。
|
| 图 3 钻杆在不同井眼曲率时下部钻具浮重 Fig.3 BHA buoyant weight with the drill pipe under different borehole curvature |
图中曲线左边为安全区域,右边为可能导致钻杆疲劳失效的区域。
1.2 复合应力下钻具的疲劳系数根据疲劳系数定义有:
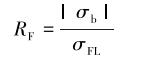
|
(16) |
式中:RF为钻具疲劳系数;σb为钻具所受的弯曲应力,MPa。
当疲劳系数大于1时,钻具发生疲劳破坏的可能性大大增加,为降低钻具疲劳破坏的可能性,应使疲劳系数尽可能小于1。通过兰德马克软件可以计算钻具每米处的疲劳系数[10]。
2 钻具设计优化实例由上述分析可知,存在较大井眼曲率的上部井段在钻具设计时既需要尽量减小疲劳系数,还需考虑到井眼曲率下部钻具的拉力对钻具失效的影响,下面以南堡3-35井为例进行分析。
2.1 优化前钻具疲劳系数该井上部井段最大井眼曲率在井深995.37 m处,每30 m井眼曲率为3.88°。常规三开钻具组合为:Ø215.9 mm钻头+直螺杆+浮阀+Ø158.8 mm无磁钻铤×1+MWD短节+Ø158.8 mm无磁钻铤+Ø127.0 mm加重钻杆×140 m+Ø127.0 mm钻杆。钻井液密度1.40 g/cm3,复合钻进钻压40 kN。
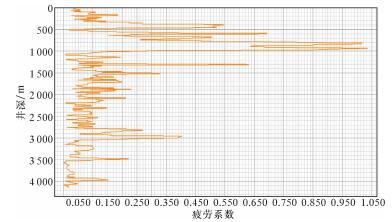
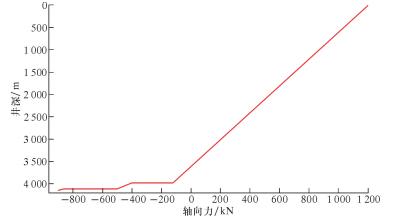
计算得南堡3-35井钻具疲劳系数及上部井段井眼曲率较大处下部钻具轴向拉力,结果如图 4和图 5所示。
|
| 图 4 南堡3-35井钻具疲劳系数随井深变化曲线 Fig.4 The fatigue coefficient of drill tool of WellNanpu 3-35 versus well depth |
|
| 图 5 南堡3-35井钻具轴向力随井深变化曲线 Fig.5 The axial force of drill tool of Well Nanpu3-35 versus well depth |
从图 4和图 5可以看出,南堡3-35井上部钻具疲劳系数较大,最大值超过1,位于井眼曲率较大井深位置附近;南堡3-35井上部井段最大井眼曲率处钻具所受力为轴向拉力,其值为856.6 kN,通过式(13)可计算该井眼曲率下Ø127.0 mm的G 105钻杆所能承受的极限轴向拉力为525.6 kN,故发生钻具疲劳失效事故可能性大大增加。
2.2 影响钻具疲劳系数的参数优化 2.2.1 钻压假设钻具不发生弯曲,计算不同钻压下上部井眼曲率较大处下部钻具所受拉力,结果见表 1。
| kN | |||||||
| 钻压 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| 拉力 | 888 | 878 | 868 | 858 | 848 | 838 | 828 |
由表 1可知,在上部井眼曲率一定的情况下,随着钻压的增大,井眼曲率下部钻具所受拉力逐渐减小,疲劳系数亦减小。因南堡3-35井下部为直井段,钻压不宜过大,建议旋转钻进钻压范围控制在50~60 kN。
2.2.2 下部钻具假设钻具不发生弯曲,调整下部钻具中加重钻杆和钻杆的长度,分别对井眼曲率较大处下部钻具所受拉力进行计算,结果见表 2。
| 加重钻杆长度/m | 220 | 200 | 180 | 160 | 140 | 120 | 100 |
| 拉力/kN | 847.2 | 839.5 | 831.9 | 824.2 | 816.6 | 809.0 | 803.0 |
由表 2可知,保持上部钻具组合方式不变,调整底部钻具组合质量,使底部钻具组合质量减小,井眼曲率下部钻具所受拉力逐渐减小,疲劳系数亦减小。
2.2.3 上部钻具考虑到上部井眼曲率较大井段疲劳系数较高,可以在上部疲劳系数较大的井段增加钻具刚性,即使用大尺寸且刚性更强的Ø139.0 mm钻杆。
假设钻具不发生弯曲,只调整上部钻具中Ø139.0 mm钻杆的长度,分别对井眼曲率较大处钻具的疲劳系数进行计算,结果见表 3。
| Ø139.0 mm钻杆长度/m | 0 | 900 | 950 | 1 000 | 1 050 | 1 100 | 1 150 |
| 疲劳系数 | 0.991 | 1.076 | 1.034 | 0.927 | 0.924 | 0.903 | 0.897 |
由表 3可知,当钻杆全部选择Ø127.0 mm钻杆时疲劳系数较大;当使用Ø139.0 mm钻杆长度小于较大井眼曲率井段井深时,疲劳系数增大;当使用Ø139.0 mm钻杆长度大于较大井眼曲率井段井深时,疲劳系数大幅减小。
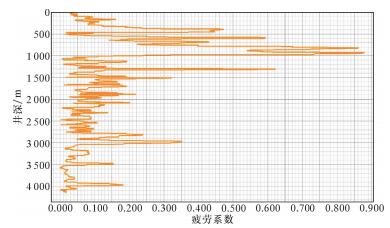
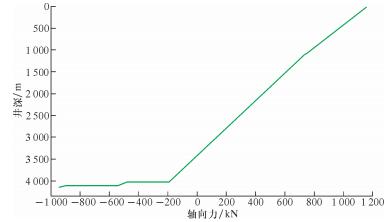
2.3 优化设计后钻具疲劳系数根据上述优化结果,对南堡3-35井钻具设计进行改进。改进后的钻具组合为:Ø215.9 mm钻头+直螺杆+浮阀+Ø158.8 mm无磁钻铤×1+MWD短节+Ø158.8 mm无磁钻铤×1+Ø127.0 mm加重钻杆×90 m+Ø127.0 mm钻杆×2 917 m+Ø139.0 mm钻杆,钻压控制为60 kN。改进后的钻具疲劳系数与井眼曲率较大处下部钻具所受轴向拉力如图 6和图 7所示。
|
| 图 6 改进钻具设计后南堡3-35井钻具疲劳系数随井深变化曲线 Fig.6 The fatigue coefficient of improved drill tool of Well Nanpu 3-35 versus well depth |
|
| 图 7 改进钻具设计后南堡3-35井钻具轴向力随井深变化曲线 Fig.7 The axial force of improved drill tool ofWell Nanpu 3-35 versus well depth |
从图 6和图 7可以看出,改进钻具设计后南堡3-35井上部钻具疲劳系数大幅减小,最大值小于1,上部井段钻具所受轴向拉力有所减小,较大井眼曲率井深处下部钻具所受轴向拉力为728.6 kN。通过式(13)计算可知,外径139.7 mm的G 105钻杆所能承受的极限轴向拉力为756.8 kN,低于在该井眼曲率下钻具所能承受的极限轴向拉力。最终在调整钻具组合后,该井三开完钻顺利,未再发生钻具疲劳失效事故。
3 结论(1)针对“S”形井和大斜度井,通过钻具力学分析并对钻井参数及钻具组合进行相关设计及优化,可以大大降低现场钻具疲劳失效事故率。
(2)在前期井眼轨迹设计中,为避免随着井眼曲率的增大,钻具疲劳系数增加,钻具能承受的极限拉力减小,现场钻井时应尽量减小浅层井段井眼曲率。
(3)优化设计后的钻具失效事故率大大降低。研究结果为今后钻具设计提供了理论和技术支持,对缩短钻井周期,节约钻井成本具有重要意义。
| [1] | 赵国珍, 龚伟安. 钻井力学基础[M]. 北京: 石油工业出版社, 1988 : 120 -125. |
| [2] | 徐灏. 疲劳强度设计[M]. 北京: 机械工业出版社, 1981 : 79 -86. |
| [3] | 刘鸿文. 材料力学[M]. 北京: 高等教育出版社, 2004 : 138 -159. |
| [4] | 石晓兵, 施太和. 弯曲井眼内下步钻柱失效研究[J]. 西南石油学院学报, 2001, 23(5): 54–57. |
| [5] | 陈绍安. 苟西003-H1井钻具失效分析报告[M]. 重庆: 中国石油川庆钻探公司川东钻探公司, 2012 |
| [6] | 潘联艺. 钻具失效情况及建议[M]. 湛江: 中海石油湛江分公司, 2012 |
| [7] | 唐继平, 梁红军. 英深1井钻柱优化设计[M]. 乌鲁木齐: 塔里木油田公司勘探事业部, 2006 |
| [8] | 王新虎. 中海油服钻杆失效[M]. 西安: 中国石油集团石油管工程技术研究院, 2013 |
| [9] | 李鹤林, 李平全, 冯耀荣. 石油钻柱失效分析及预测[M]. 北京: 石油工业出版社, 1995 |
| [10] | ZOANNI R, EVERAGE S, WADSWORTH T M, et al.Further developments in drill pipe fatgue management:A case study[R].SPE 119903, 2009. |



