2. 上海海隆石油管材研究所;
2. Shanghai Engineering Research Center for Petroleum Tubular Goods
0 引言
随着石油钻探技术的发展,陆地深层和深海油气资源相继进入勘探开发阶段,钻具的服役环境和工况变得越来越复杂,这直接推动了油田对钻具智能化管理系统的需求。基于该需求,通过应用钻柱力学分析和钻具疲劳寿命理论,形成综合考虑井眼轨迹、钻具组合、钻井液性能和操作参数等因素的钻具疲劳寿命评估技术,建立智能化钻具管理系统,实现钻具的智能评价管理、监控预警和跟踪追查,从而减少钻具失效事故的发生,减低钻井成本。钻具疲劳寿命的智能化管理将是工业4.0发展下智能钻井的一个重要分支,而钻具疲劳寿命评估模型则是钻具智能化管理系统的核心方法。
长期以来,国内外学者对钻杆疲劳寿命预测方法[1]的研究主要集中在采用小试样模拟试验研究、钻杆实物疲劳试验研究及理论计算研究等方法上,但能将多种方法相互结合形成完整的预测系统并应用的报道较少。这些钻杆疲劳寿命预测方法的研究理论基础实质上主要基于累积疲劳损伤理论和断裂力学理论。在各种方法中,以文献[2]中的方法最为经典,即认为钻具经过“狗腿”井段时受循环弯曲作用力,当弯曲应力足够大时,钻具在每一个旋转周次中都将发生疲劳损伤。基于该疲劳累积经典理论,文献[2]提出一种简易的方法来估算钻杆通过狗腿段后的累积疲劳损伤,定制了腐蚀介质和非腐蚀介质中E钢级在不同狗腿严重度和拉力下消耗的寿命。但该方法使用局限性较大,仅针对E钢级,未考虑高钢级情况,并且只能作为“卡片式”计算,不满足对整口井钻杆动态累积疲劳损伤的评估。之后国内很多学者也相继进行研究[3-5],但与现场数据对接情况和模型应用成果均未见报道。笔者通过研究近年来国外石油钻杆疲劳寿命预测系统模型和应用情况,分析了现有模型存在的问题,并提出钻杆疲劳寿命预测系统模型发展的新趋势,以期为我国在钻具智能管理系统的研究提供参考。
1 国外主要钻杆疲劳寿命预测系统模型及应用 1.1 基于Miner法则的疲劳累积损伤模型与应用疲劳累积损伤理论的基本假设是:构件在任何循环应力幅下工作都将产生疲劳损伤,疲劳损伤的严重程度和在该应力幅下工作的循环周次有关,且与无循环损伤的试样在该应力幅下产生失效的循环数有关[6-7]。疲劳累积损伤理论总体上可分为线性疲劳累积损伤理论和非线性疲劳累积损伤理论。在石油钻具上应用较多的是基于Miner法则的线性累积疲劳损伤[2, 8-9]。该法则认为,材料在各级应力下的疲劳损伤是独立的,因而总损伤可以按线性形式累加起来。模型主要理论包括材料S-N曲线、等寿命公式、疲劳损伤累积法则和失效准则。材料的S-N曲线为应力-疲劳寿命曲线,是金属材料在弹性范围内发生的疲劳失效。S-N曲线的表达式一般通过光滑试样在恒幅载荷下的旋转弯曲疲劳试验数据拟合获得。而钻具实际服役过程中所受到的载荷为变幅载荷,工程应用上常用等寿命法则计算变幅载荷下的平均应力。
U.B.SATHUVALLI等[10]通过机械设计方法研究总结了一种S-N曲线的表达式,并通过与钻杆经典疲劳试验数据拟合对比,拟合结果曲线与文献[2]推荐的W.S.BACHMAN[11]试验数据符合,S-N曲线在无腐蚀环境中的具体表达式为:

|
(1) |
式中:Sf(Sm,N)为在N次循环和平均应力Sm下的疲劳强度,MPa;a、b为常数,分别由下式计算得到:
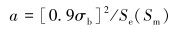
|
(2) |
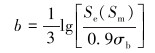
|
(3) |
式中:σb为材料的抗拉强度,MPa;Se(Sm)是当N=1×106时的疲劳强度,即Se(Sm)=Sf(Sm,106)。
钻杆在实际应用过程中,给定钻具在每个计算步长的井段内所受到的平均应力Sm不同,应考虑平均应力的影响。而S-N曲线是恒幅载荷条件下试验或设计得到的曲线关系,不能直接将平均应力带入S-N曲线公式求该应力水平对应的疲劳强度。工程上常采用Goodman法则[6]计算任意平均应力幅下对应的疲劳强度Sf(Sm,N):
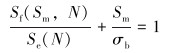
|
(4) |
式中:Se(N)为疲劳极限,MPa。
将式(4)得到的本井段的平均应力幅对应的疲劳强度Sf(Sm,N)带入S-N曲线中,可以得到在第i个该平均应力作用下材料达到破坏的极限循环次数N。
将整口井钻具按一定步长划分,第i个计算步长井段内钻具所受到的平均应力Sm(i)所对应的旋转周次为ni,在该应力水平下钻杆材料极限循环次数为Ni,旋转周次计算式为:
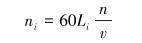
|
(5) |
式中:Li为第i个平均应力水平Sm(i)作用下钻杆所钻深度,m;n为转盘转速,r/min;v为机械钻速,m/h。
则在该级应力水平下钻杆的疲劳损伤Di为:
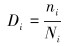
|
(6) |
各级应力对材料的损伤总和Dm为:
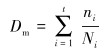
|
(7) |
式中:t为应力级数。
当Dm=1时认为钻杆将发生失效。
该计算方法最重要的部分在于正确评估钻杆特定部位所受到的平均应力。A.LUBINSKI[12]早前提出了受拉情况下钻杆在狗腿段的弯曲应力的计算,P.R.PASLAY[13]考虑了受压情况并提出改进。W.JIANG[14]提出了综合2种情况接头附近管体的最大弯曲应力计算:
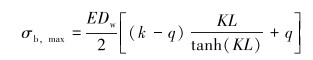
|
(8) |
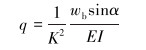
|
(9) |
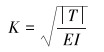
|
(10) |
式中:σb,max为最大弯曲应力,MPa;E为钢的弹性模量,MPa;Dw为井眼直径,m;k为每30 m的井眼曲率,(°);α为井眼井斜角,(°);wb为单位长度钻杆的浮重,N/m;T为轴向力,N;I为钻杆管体的转动惯量,m4;L为钻杆半长,m。
A.SIKAL等[15]在上述研究的基础上,认为循环弯曲应力幅值由轴向载荷类型(拉或压)、轴向载荷幅值和钻杆与井眼的接触情况有关。A.LUBINSKI和P.R.PASLAY建议的计算特定狗腿段钻杆应力的方法是基于钻杆与井壁接触的假设上的,具有一定局限性,提出了采用数值模型方法计算钻杆不同位置的应力分布。对于任何给定的钻杆,如已知钻杆弯矩和施加的轴向载荷后,循环应力Scyclic为:
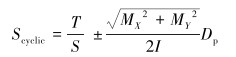
|
(11) |
式中:S为钻杆截面积,m2;Dp为钻杆外径,m;MX和MY分别为钻杆所受弯矩沿X、Y方向的分量,N·m。
将循环应力Scyclic分为2部分:轴向应力分量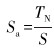
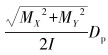
在实际应用中,结合拉力扭矩模型或数值模型分析软件ABIS[16-17]可以确定钻杆上任何给定区域的应力,且不用做任何钻杆和井眼接触的假设。这种数值模型可分析从井口到钻头的钻柱受力情况,可计算沿钻柱任何位置的受力情况。
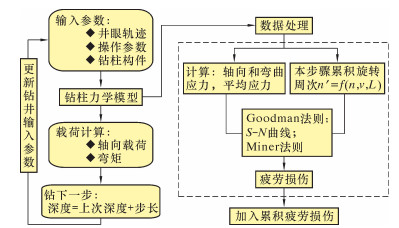
软件迭代计算流程如图 1所示。将钻杆钻井过程的最初深度Lmin到目标深度Lmax按照给定的步长增量进行迭代计算,即将第i个步长的钻井参数导入钻柱力学模型(ABIS)软件,计算该级拉伸载荷和弯矩,得到的受力结果导入到数据处理/疲劳寿命分析程序中,计算平均应力和该级应力水平下的旋转周次ni,通过Goodman法则和S-N曲线计算出失效循环周次N,采用Miner法则计算累积疲劳损伤。
|
| 图 1 软件迭代计算流程 Fig.1 Software iterative calculation process |
该软件模型应用的第1口井是水平井,井深4 000 m,造斜段每30 m狗腿度为6°,水平段长约1 000 m。所追踪评价的钻杆为从700 m (造斜点附近)处一直钻到目标井深。按照上述迭代计算流程进行各项计算,其中被追踪钻杆的弯曲应力分别采用A.LUBINSKI/P.R.PASLAY的计算方法与数值分析软件进行计算对比。经累积疲劳损伤程序计算,弯曲应力用ABIS模型分析的累积损伤结果为48%,而用A.LUBINSKI/P.R.PASLAY计算弯曲应力方法得到的累积损伤为6%,相差8倍,研究者认为这个差别是由传统弯曲应力计算将钻杆弯曲曲率与井眼曲率视为一致引起的。
日本海洋研究开发机构(JAMSTEC)在“Japan Trench Fast Drilling Program (FAST)”项目[18-20]中利用地球号钻井船(CHIKYU)对海槽地震带钻探研究海洋强流对钻杆疲劳损伤中,结合实物疲劳试验也采用累积疲劳损伤理论进行评估。该系统提前计算了弯曲应力的分布,存入数据库中,与实时钻井参数共同应用于实时评价系统中。这种方法虽然简便,但实际钻井中钻杆的受力情况与预测的有所差别,疲劳累积损伤计算结果将受到影响。
1.2 基于疲劳寿命标准化的断裂力学模型和应用线弹性断裂力学模型主要针对稳态阶段疲劳裂纹扩展寿命的计算,常用于钻具疲劳寿命预测的模型主要有Paris模型和Forman模型[21]。近几年的研究中,我国学者考虑了扭矩对钻杆的影响,逐渐出现拉、弯、扭复合载荷作用下裂纹的扩展速率公式[22-23],即Ⅰ型(张开型)和Ⅲ型(撕开型)裂纹扩展速率公式的线性叠加。但这些研究仅停留在研究层次,尚未有相关现场实际应用成果的报道。
国外使用线弹性断裂力学模型进行钻具疲劳寿命评估效果最为突出的是美国T.H.Hill Associates lnc.公司。其所用的模型已经成功在油田现场上使用,部分计算方法已载入DS-1标准[24]中。该系统模型的核心部分在于钻具弯曲指数的计算算法和与拉力扭矩计算程序的联合应用[25-26],模型首先计算井壁曲率c和临界曲率cc,并进行比较,用于选择钻杆弯矩的计算公式。
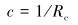
|
(12) |
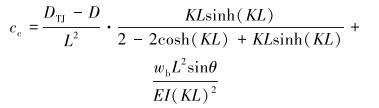
|
(13) |
式中:Rc为井眼曲率半径,m;DTJ、D分别为钻杆接头和管体外径,m;θ为钻杆管体的平均倾斜角,rad。
当c < cc,钻杆管体没有接触井壁,采用式(14)计算M0;当c≥cc,钻杆管体接触井壁,则采用式(15)计算M0。
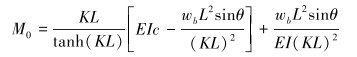
|
(14) |

|
(15) |
式中:rc为接头和井眼的径向间隙,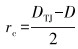
计算钻杆受到的弯曲应力σb和轴向应力σa:
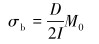
|
(16) |
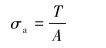
|
(17) |
式中:A为钻杆管体横截面积,m2。
则裂纹尖端的应力强度因子计算式为[27]:
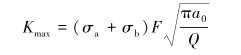
|
(18) |

|
(19) |
式中:a0为假设已存裂纹的最大深度,m;F为裂纹形状校正因子;Q为构件几何校正因子;Kmax、Kmin分别为最大应力强度因子和最小应力强度因子,MPa·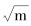
计算应力比R的计算式为:
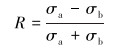
|
(20) |
若R>0时,ΔK=Kmax-Kmin;若R≤0时,ΔK=Kmax。当ΔK≤0,裂纹不扩展;当ΔK>0,则裂纹发生稳态扩展,其扩展速率采用Forman公式:
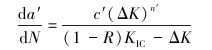
|
(21) |
式中:c′为公式系数;n′为公式指数;ΔK为应力强度因子变化幅值,MPa·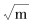
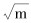
此时可计算钻杆达到失效的旋转周次N:
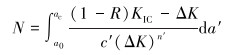
|
(22) |
式中:ac为临界裂纹深度,m。
以弯曲指数CI为代表的标准化疲劳寿命计算式为:
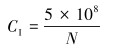
|
(23) |
则在该应力状态下的累积疲劳损伤点DPi为:
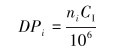
|
(24) |
全井段单根钻杆上累积的疲劳损伤点为钻杆在所有位置受到的疲劳损伤点的线性累加,即有:
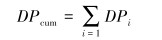
|
(25) |
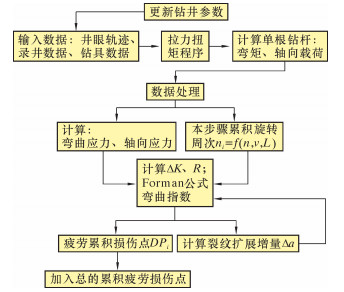
该模型在计算某时刻某一位置钻杆的轴向载荷和弯矩需要借助拉力扭矩程序进行计算。软件的计算思路框图如图 2所示。
|
| 图 2 软件计算思路框图 Fig.2 Software calculation block diagram |
软件中可规定一个计算步长以循环迭代计算,输入每一步的钻井参数、录井数据及钻具参数等,通过拉力扭矩程序计算出某一时刻某一位置计算点钻杆的弯矩和轴向载荷,经数据处理输出弯曲应力、轴向应力以及对应步长的旋转周次,计算应力因子变化幅值、应力比、失效循环周次和弯曲指数等中间参数,进而可计算对应计算步骤的疲劳损伤点,最终线性累加至总的疲劳损伤点中。在循环计算中需计算裂纹增量。该软件最终结果呈现每个井段和全井段钻具累积疲劳损伤与井深的分布曲线。
这种模型累积疲劳损伤点临界值的确定采用失效追算的方法验证,即将多口钻具失效井数据带入软件中进行计算,得到发生失效时的临界损伤点。DS-1标准推荐,启动检测的触发点为500~700个损伤点之间。经计算机程序编写形成软件,并作为设计阶段的预测和钻井实时监测使用。阿根廷Pluspetrol石油作业公司在秘鲁Pagoreni油田56号区块的钻探中,因1003D井多次发生刺漏失效,在其余3口井Pag1004D井、Pag1005D井和Pag1006D井采用累积疲劳损伤评估软件对所用的钻杆进行钻前预测和实时监测,并成功指导Pag1006D井的钻具倒换和检测[27]。
值得注意的是,由于模型是建立在假设预先存在裂纹的基础上,对钻具要求极严格的钻前检测以确保钻杆可能存在的裂纹尺寸小于目前设备的可检测极限。该模型在循环期间或在钻井中机械钻速低于设计值且有过多的倒划眼和旋转,则可能发生疲劳损伤急剧增加,并大大超过钻前预测值。
2 智能化钻具疲劳寿命评估管理系统的未来发展趋势基于Miner法则的累积疲劳损伤模型主要基于经典疲劳强度理论,方法简单且易于执行。其缺点在于:①没有考虑应力集中系数。实验室S-N曲线的测定在抛光试样上进行,实际上钻杆在使用过程中将不可避免地受到划伤和腐蚀等作用形成缺口,引起应力集中。②没有考虑腐蚀对疲劳的影响。③加载顺序对失效准则的影响。高低载荷的加载次序不同,Dm值大小也不相同,通常采用的Dm=1发生失效,仅为平均载荷的结果,国内学者[28]曾对该值修正为0.68。
将疲劳寿命标准化的断裂力学模型假设预先存在微裂纹,以疲劳裂纹的第Ⅱ阶段稳态扩展为基础进行迭代计算,并以裂纹扩展到临界深度ac或裂纹尖端应力KIC场强度因子达到为失效依据。这对于新钻杆可能会导致计算结果偏于保守,造成过早进行钻具检测而导致检测费用较大。此外,模型中断裂力学参数的确定为难点,可通过经验公式、仿真模拟以及试验获得,但数值的准确性有待深究。该模型通过计算弯曲指数将疲劳寿命标准化,即将5×108视为极限疲劳寿命,在软件实现迭代计算中,与拉力扭矩程序相互作用并循环计算。
国内外对钻具疲劳问题的研究持续了将近100 a,但钻具疲劳失效仍然是引起钻具失效的主要原因。在工业4.0发展背景下,钻具疲劳寿命的智能化管理将是提高钻具管理效率和减少钻具发生疲劳失效的重要手段。
通过研究目前国外石油钻具疲劳寿命预测模型,认为今后钻具疲劳寿命智能化管理系统的研究应建立在前人研究的基础上,同时结合各种理论模型的优缺点,着重考虑以下几个发展方向:①考虑腐蚀对疲劳寿命评估的影响,腐蚀对疲劳寿命的影响很难量化,但可以通过实物试验研究和设计不同环境的系数来表征腐蚀对疲劳寿命的影响。②无论采用哪种模型,应重点考虑将各种预测方法有机结合形成完整的疲劳寿命预测及管理系统。可先由实验室小试样疲劳试验得到S-N曲线或进行断裂韧性试验得到模型的参数公式,并由实物疲劳试验验证,修正软件系统的各种参数算法,提高模型准确性。③与接头的疲劳寿命评估相结合,得到钻具的完整性疲劳寿命评估和管理。④与有限元分析方法相结合,从理论上进一步验证。钻杆疲劳寿命的计算分析常采用有限元分析方法,但因钻井井况复杂,不同位置、不同时刻的钻杆受到的边界条件不一样,软件设计中通过有限元方法分析钻具动态疲劳特点,有助于模型的建立和修正。断裂力学参数可通过有限元仿真计算确定。⑤与RFID (射频识别技术)相结合,详细记录各种使用信息,实行智能化全方位钻具管理。⑥钻具的疲劳寿命评估最终应作为钻具倒换、检测频次要求及钻杆分级的重要理论依据之一。
3 结束语国外石油钻杆疲劳寿命预测系统的模型主要有基于Miner法则的疲劳累积损伤模型和基于疲劳寿命标准化的断裂力学模型,2种模型均已在现场试用或应用,后者被纳入DS-1标准作为重新制定钻具检测的依据。
钻具疲劳寿命智能化管理的研究方向应重点考虑腐蚀对疲劳寿命的影响,同时与接头疲劳寿命评估、RFID、有限元分析方法以及钻具检测分级要求相结合,形成智能化管理系统,力求达到钻具疲劳寿命完整性、智能化评估和管理。
| [1] | 李方坡, 王勇. 钻杆疲劳寿命预测技术的研究现状与展望[J]. 材料导报A, 2015, 29(6): 88–95. |
| [2] | HANDSFORD J E, LUBINSKI A. Cumulative fatigue damage of drill pipe in dog-legs[J]. Journal of Petroleum Technology, 1966(3): 359–363. |
| [3] | 路永明. 水平钻井钻柱疲劳损伤的评估[J]. 石油学报, 1999(6): 73–76. |
| [4] | 林元华, 罗宏志, 邹波, 等. 钻柱失效机理及其疲劳寿命预测研究[J]. 石油钻采工艺, 2004(1): 19–22. |
| [5] | 李文飞. 基于可靠性理论的钻柱疲劳寿命预测[J]. 石油钻采工艺, 2008, 30(1): 12–14. |
| [6] | 郑修麟, 王泓, 鄢君辉, 等. 材料疲劳理论与工程应用[M]. 北京: 科学出版社, 2013 : 124 -126. |
| [7] | 刘伟建. 疲劳累积损伤理论发展概述[J]. 山西建筑, 2008, 34(23): 76–78. |
| [8] | MORGAN R P, ROBLIN M J.A method for the investigation of fatigue strength in seamless drillpipe[C]//1969 ASME Conference.Tulsa, 1969:227. |
| [9] | AMRO M M. Equations predict drill pipe fatigue[J]. Oil and Gas Journal, 2000(7): 36. |
| [10] | SATHUVALLI U B, PAYNE M L, PATTILLO P D, et al.Advanced assessment of drillpipe fatigue and application to critical well engineering[R].SPE/IADC 92591, 2005. |
| [11] | BACHMEN W S. Fatigue testing and development of drill pipe to tool joint connection[J]. World Oil, 1951, 12(1): 104. |
| [12] | LUBINSKI A. Maximum permissible doglegs in rotary boreholes[J]. Journal of Petroleum Technology, 1961, 13(2): 175. 10.2118/1543-G-PA |
| [13] | PASLAY P R.Bending stress magnification in constant curvature doglegs with impact on drill string and casing[R].SPE 22457, 1991. |
| [14] | JIANG W.Drill-pipe bending and fatigue in rotary drilling of horizontal wells[R].SPE 37353, 1996. |
| [15] | SIKAL A, MENAND S, SELLAMI H.Drill pipe stress and cumulative fatigue analysis in complex wells drilling:New approach in fatigue optimization[R].SPE 116029, 2008. |
| [16] | SIKAL A, MENAND S, SELLAMI H J.How drillstring rotation affects critical buckling load[R]. IADC/SPE 112571, 2008. |
| [17] | MENAND S, SELLAMI H J, STAB O, et al.Advancement in 3D drillstring mechanics:From the bit to the topdrive[R].IADC/SPE 98965, 2008. |
| [18] | INOUE T, OZAKI M, MIYAZAKI T. Maximum stress and fatigue strength of drill pipe in presence of strong ocean current[J]. International Journal of Offshore and Polar Engineering, 2010, 20(1): 15–17. |
| [19] | INOUE T, KYOM, SAKURA K.Fatigue strength evaluation of drill pipe for challenging deep drilling project-Japan trench fast drilling (JfAST)[C]//2013, Proceeding of 2013 International Offshore and Polar engineering.Alaska, 2013:128-134. |
| [20] | INOUE T, FUKUI K S.Fatigue strength investigation of drill pipe for challenging scientific deep drilling and utilization of drilling data to estimate cumulative fatigue[R].OTC-25140, 2014. |
| [21] | 张杰, 马永亮. 3种疲劳裂纹扩展速率模型比较[J]. 实验室研究与探索, 2012, 31(8): 35–38. |
| [22] | 艾池, 盖伟涛, 王黎明. 钻柱在扭转、纵向振动下的疲劳寿命估算[J]. 大庆石油学院学报, 2006, 30(4): 9–11. |
| [23] | 夏天果, 朱红钧, 王攀, 等. 一种预测钻柱疲劳失效的新方法[J]. 石油矿场机械, 2011, 40(9): 6–9. |
| [24] | HILL T, ELLIS S, KAN L, et al.An innovative design approach to reduce drillstring fatigue[R]. IADC/SPE 87188, 2004. |
| [25] | GOKHALE S R, ZOANNI R, ZHENG N J, et al.Advances in drillpipe fatigue management[R]. SPE 110076, 2007 |
| [26] | BERT D, STRAUNE A, ZHENG N J.Case study:Drillstring failure analysis and new deep-well guidelines lead to success[R].SPE 110708, 2007. |
| [27] | ZOANNI R F, EVERAGE S D, WADSWORTH T M, et al.Further developments in drill pipe fatigue management:A case study[R].SPE/IADC 119903, 2009. |
| [28] | 李文飞, 管志川, 赵洪山, 等. 钻柱疲劳累积损伤的计算方法[J]. 中国石油大学学报(自然科学版), 2008, 32(3): 60–62. |




