0 引 言
弯管是管路系统的重要管件之一,主要作用有2方面:一方面根据需要改变管线的方向;另一方面提高管路柔性,通过弹性或塑性变形减小管路系统中由于热膨胀等因素产生的力和力矩[1-3]。弯管在实际工作中除承受内压外,还承受弯矩、扭矩和自重等载荷的作用,是管路系统中的薄弱环节[4]。弯管应力的理论计算方法中一般将其理想化为均匀壁厚,但是实际弯管受制造工艺限制,壁厚具有不均匀性[5]。笔者提出一种新的弯管建模方法,建立新的壁厚不均匀弯管有限元模型,通过实例分析在内压与弯矩联合作用下弯管的应力分布,以期为实际弯管的设计制造及安全评价提供依据。
1 弯管模型的建立对于壁厚不均匀的弯管,文献[6]利用偏心圆法建立有限元模型。该方法将截面内壁圆的圆心向外侧偏移定值e,所建立的弯管有限元模型仅体现了弯管横截面上的壁厚不均匀性。工程用弯管不仅经向存在不均匀性,而且周向也存在不均匀性。定偏心距建模方法会使弯管与直管连接处的壁厚不连续,导致出现附加边缘力。
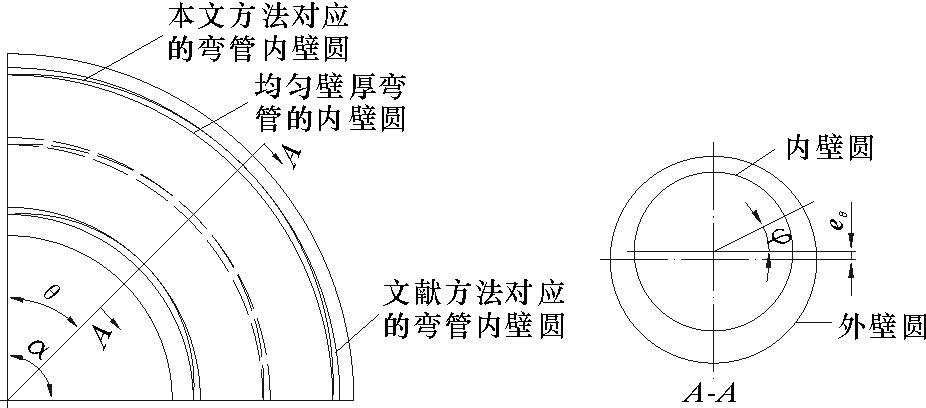
均匀壁厚弯管的中面可以看成是以圆为经线的回转薄壳的一部分,为严谨起见,笔者将φ方向称为经线方向,θ方向称为周向,不沿用工程上的“环向”和“轴向”称谓,弯管模型见图 1。通过对偏心圆法进行改进,使偏心距e随弯管周向角度θ而变化。根据生产用热煨弯管的壁厚测量结果,偏心距eθ可近似表示为:
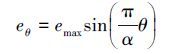 (1)
(1) 式中:eθ弯管任意周向角度θ对应的偏心距,m;α弯管的转角;emax弯管的最大偏心距,等于弯管壁厚的最大增厚值或最大减薄值,m,该值与弯管平均壁厚的比值可表征弯管壁厚的不均匀程度。
|
| 图 1 改进偏心圆法对应的弯管模型示意图 Fig.1 Schematic of elbow model corresponding |
依据SY/T 5257—2004《油气输送用钢制弯管》中壁厚最大减薄率应不大于9%的规定,笔者研究弯管的壁厚不均匀程度不超过9%。
2 模型可靠性验证 2.1 建模方法及模拟条件建立不均匀壁厚弯管有限元模型时选择3D实体单元——20node的Solid95单元,选用映射网格,并对弯管以及与其相连的直管部分的网格疏密进行有差别控制[7-8]。网格划分:径向为10等分,经向为72等分,弯管段周向为90等分,直管段轴向为20等分,模型共划分了79 200个单元。
采用国内某特大型高含硫气田所用弯管作为算例,外径D=0.508 m,设计壁厚t0=0.022 2 m,曲率半径R=2.03 m,转角α=90°。为了消除端部效应,选取与弯管相连的直管段长度L=2 m,大于3倍的管径。管材弹性模量E=205 GPa,泊松比ν=0.3,最低屈服强度σs=360 MPa,材料服从各向同性假设及小变形假设。
长输管道工程中的弯管主要受到内压与弯矩的联合作用,其他载荷相对较小,可以忽略,因此笔者对内压与弯矩联合作用下的弯管进行分析。模拟的边界条件:弯管一端施加约束进行固定,另一端自由。由于考虑内压作用,需在自由端施加等效周向拉应力pri2/(r2o-ri2)[9]。由于考虑弯矩作用,需在自由端建立Mass21单元节点,并与端部横截面耦合形成刚性整体[10]。
为方便与理论值进行对比验证,不妨设eθ=0,弯矩M=0。此时相当于纯内压作用的均匀壁厚弯管。内压作用下均匀壁厚弯管中性面上的应力分布可以由无力矩理论求得。考虑弯管壁厚影响,基于力平衡方程可以得到更精确的均匀壁厚弯管平均应力公式[11]。 经向应力为:
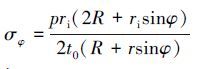 (2)
(2) 周向应力为:
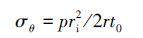 (3)
(3) 式中:σφ为经向应力,MPa;σθ为周向应力,MPa;R为弯管曲率半径,m;r为弯管中面半径,m;ri为弯管内半径,m;ro为弯管外半径,m;φ为弯管横截面上的角度,根据图 1,规定内弯侧为-90°,外拱侧为90°;p为管道内压,MPa;t0为管道壁厚,m。长输管道用弯管大多由直管弯制而成,为了方便与直管应力相比较,工程上也常将弯管的经向应力和周向应力称为环向应力和轴向应力。
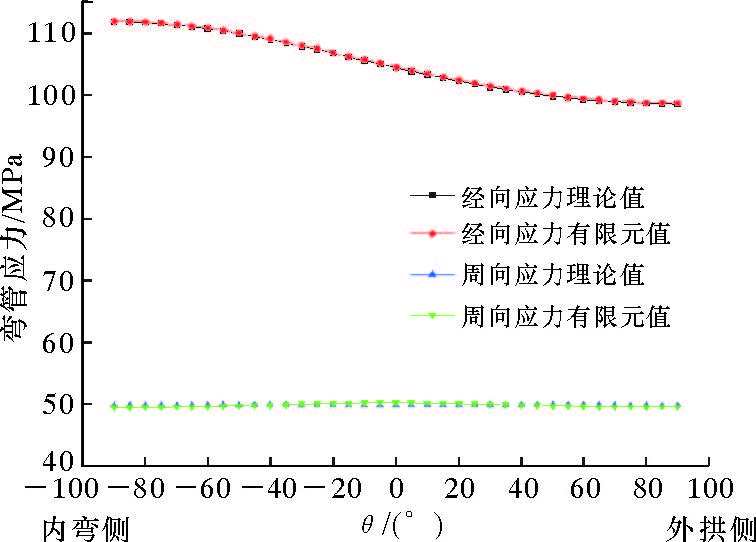
2.2 结果验证运用上述建模方法,模拟得到内压为10 MPa作用下均匀壁厚弯管的经向应力与周向应力结果,并与理论公式(2)和式(3)计算结果相比较,结果见图 2。
|
| 图 2 弯管θ=45°横截面上应力有限元值与理论值的比较 Fig.2 The finite element stress value and the theoretical value of the cross-section where elbow θ=45° |
由图 2可知,不论经向应力还是周向应力,理论值与有限元值基本一致。经向应力相对误差的平均值为0.11%,最大值为0.14%;周向应力相对误差的平均值为0.47%,最大值为0.77%。误差满足有限元模型准确度的要求,因此笔者所提出的弯管建模新方法可行,模型划分的节点足够多。
3 壁厚不均匀性对弯管应力的影响 3.1 弯管的应力分布大型工程中由直管弯制弯管时,弯制力矩造成外弧区壁厚减薄,内弧区壁厚增加,对这种壁厚不均匀的弯管,目前没有计算的精确解[12]。笔者利用上述弯管模型方法建立算例,对内压10 MPa与面内闭合弯矩0.5 MN·m联合作用下均匀壁厚与不均匀壁厚的弯管进行有限元模拟,分析得到弯管的经向应力与周向应力分布规律,如图 3所示。

|
| 图 3 弯管θ=45°横截面上的应力分布图(emax/t0=0%,9%) Fig.3 Stress distribution of the cross-section where elbow θ=45° (emax/t0=0%,9%) |
由图 3可以看出,均匀壁厚弯管与不均匀壁厚弯管应力分布的整体趋势基本一致。为了更深入地分析壁厚不均匀性对弯管应力分布的影响,将θ=45°横截面上的经向应力与周向应力分离为薄膜应力、一次弯曲应力和二次弯曲应力,结果如图 4~图 7所示。详细的分析中还会出现泊松应力和弯管曲率变化引起的附加应力,由于它们数值较小,对弯管的安全可靠性影响甚微,所以不做分析。
|
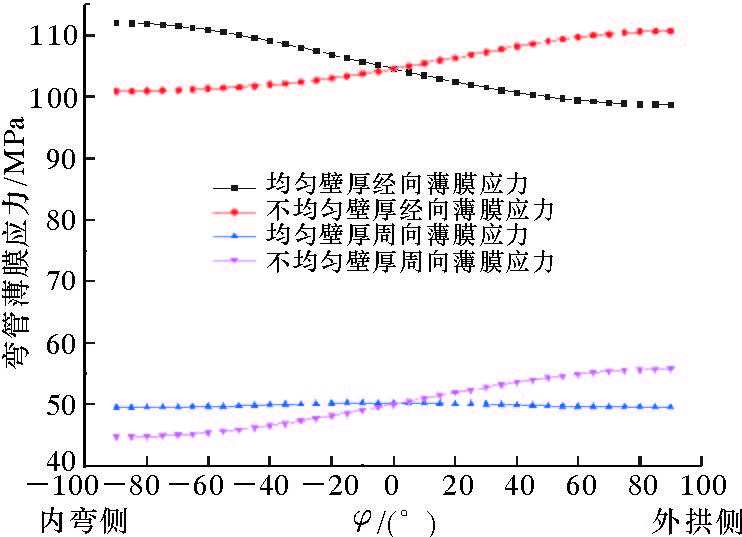
| 图 4 弯管θ=45°横截面上的薄膜应力 Fig.4 Membrane stress distribution of the cross-section |
|
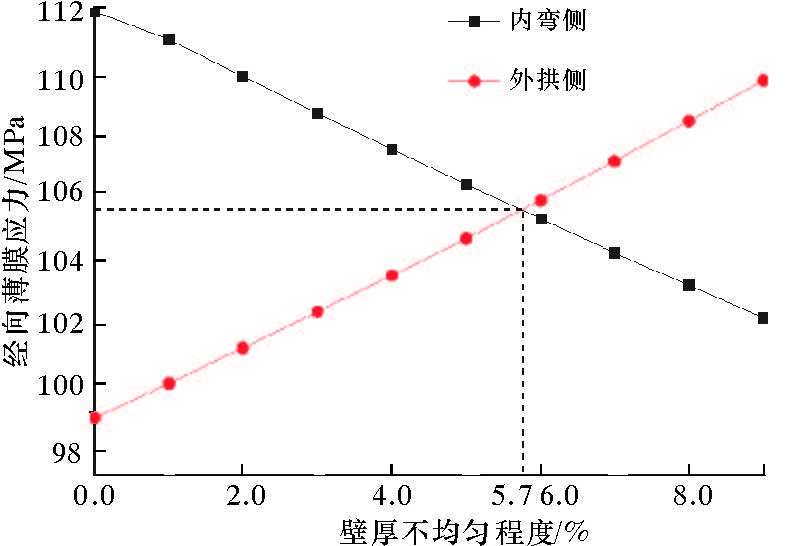
| 图 5 弯管薄膜应力与壁厚不均匀程 Fig.5 The effect of non-uniform thickness on elbow |
|
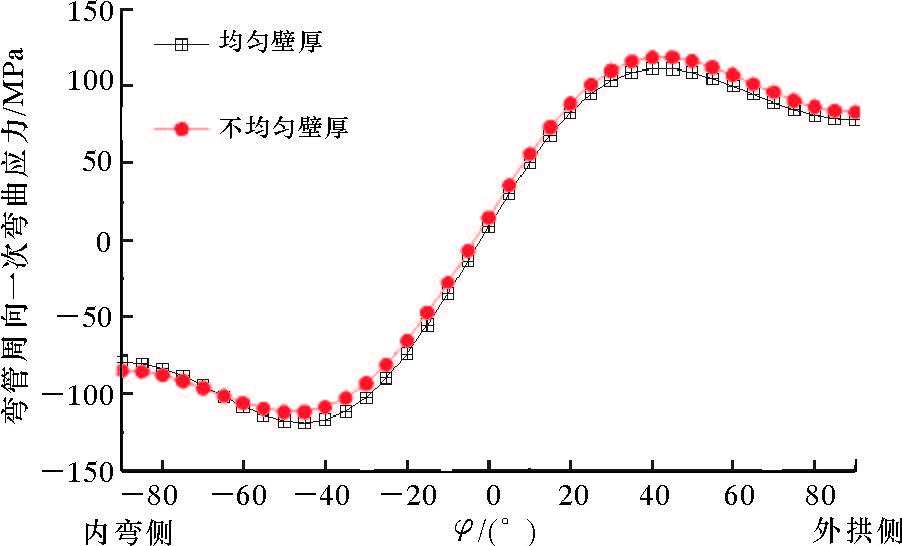
| 图 6 弯管θ=45°横截面上的一次弯曲 Fig.6 The once bending stress distribution of the cross- |
|
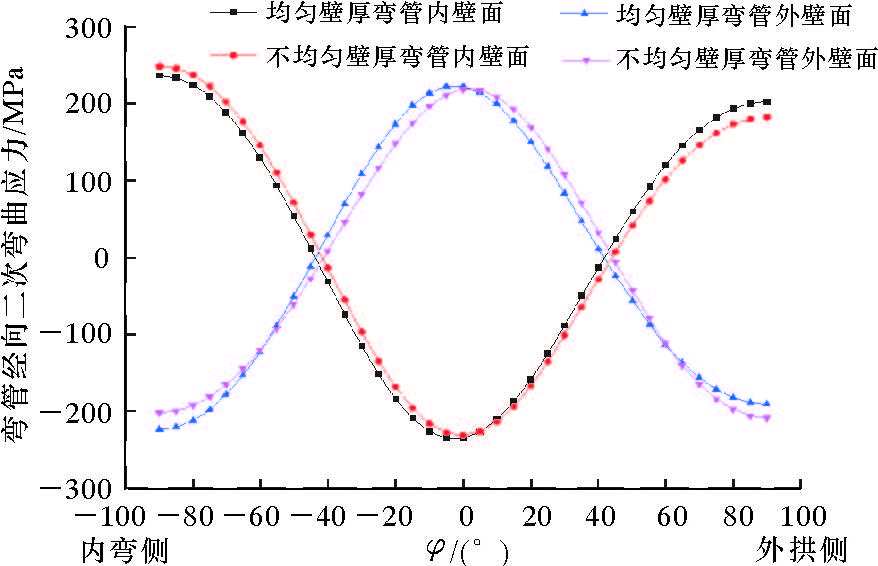
| 图 7 弯管θ=45°横截面上的经向二次弯 Fig.7 The radial secondary bending stress distribution of the |
由图 4可知,均匀壁厚弯管的经向薄膜应力由内压产生,从内弯侧到外拱侧逐渐减小,最大值位于内弯侧,周向薄膜应力基本不变。由于壁厚不均匀性的影响,外拱侧壁厚减薄,薄膜应力增大。内弯侧壁厚增加,薄膜应力减小。对于弯管肩部(φ=0°),壁厚变化很小,因此薄膜应力基本不变。
图 4所示的算例中,emax/t0=9%,最大经向薄膜应力所在位置出现在外拱侧,而均匀壁厚弯管的最大经向薄膜应力所在位置出现在内弯侧。可推知,在壁厚不均匀程度增大的过程中,弯管的内弯侧经向薄膜应力逐渐减小,外拱侧逐渐增大。当壁厚的不均匀性增大到一定程度时,最大经向薄膜应力所在位置会由内弯侧突变到外拱侧。为了确定算例中最大经向薄膜应力所在位置突变时对应的壁厚不均匀程度的准确值,笔者对emax/t0=0%~9%的弯管进行一系列模拟,提取出内弯侧与外拱侧的经向薄膜应力,结果如图 5所示。由图可知,算例中,当emax/t0=5.7%时,弯管的内弯侧与外拱侧的经向薄膜应力相等,此时的最大经向薄膜应力为 105.49 MPa。因此,适当的壁厚不均匀性有利于降低经向薄膜应力的不均匀性,也就是说,适当的壁厚不均匀有利于增强弯管承受内压的能力。
由图 6可知,由于弯管柔性的影响,从内弯侧到外拱侧的一次弯曲应力不再是线性分布,而是呈现出复杂的形态。由于本算例所示均匀壁厚弯管的特征数(h=Rt/r2=0.7638)较小,小于1.472,故最大一次弯曲应力向内侧严重偏离,出现在φ≈±43°的位置。与均匀壁厚弯管相比,不均匀壁厚弯管的内弯侧由于壁厚增大,刚度加强,最大一次弯曲压应力有所减小,位置也向外侧有所偏离。外拱侧由于壁厚减薄,刚度降低,最大一次弯曲拉应力变大,但位置变化不大。最大一次弯曲拉应力的增大使得弯管强度降低,因此用于不均匀壁厚弯管强度校核的周向弯曲应力增强系数应适当增大。
弯矩作用下弯管的圆截面呈椭圆化变形趋势,因而会产生经向二次弯曲应力(见图 7)。均匀壁厚弯管和不均匀壁厚弯管的经向二次弯曲应力的整体分布趋势一致,可以近似用正弦曲线表征,极值出现在φ=0°、180°和±90°。经向二次弯曲应力的数值远大于周向一次弯曲应力。对于弯矩作用下的弯管,经向二次弯曲应力的校核对保证弯管的强度和寿命至关重要。数值计算结果表明,对于不均匀壁厚弯管,最大经向二次弯曲应力出现在壁厚最厚的内弯侧,而不是壁厚较薄的外拱侧,比均匀壁厚弯管有所增大,因此用于不均匀壁厚弯管强度校核的经向弯曲应力增强系数应适当增大。
3.2 弯管的应力最大值及位置弯管应力最大值的位置是弯管上可能的最危险区域。算例中均匀壁厚与不均匀壁厚弯管的各项应力的最大值及位置见表 1。由表可以看出,对于均匀壁厚弯管,除了经向二次弯曲应力外,其他应力的数值解与理论解基本接近。经向二次弯曲应力一次近似解误差较大,达不到工程应用程度。根据文献和本文数值计算,最大经向二次弯曲应力的数值约等于2.1倍最大周向一次弯曲应力。
不均匀壁厚弯管的应力分布规律受很多因素影响,更详细的分析需要进一步研究,将另文详述。
| 应力名称 | 方向 | 均匀壁厚弯管理论值/MPa | 均匀壁厚弯有限元值/MPa | 不均匀壁厚弯管有限元值/MPa | |||
| 数值 | 位置 | 数值 | 位置 | 数值 | 位置 | ||
| 经向应力 | 经向 | — | — | 346.56 | φ=-90°内壁面 | 331.54 | φ=-90°内壁面 |
| 周向应力 | 周向 | — | — | 195.06 | φ=25°外壁面 | 210.64 | φ=30°外壁面 |
| 薄膜应力 | 经向 | 111.83 | φ=-90° | 111.79 | φ=-90° | 110.03 | φ=90° |
| 薄膜应力 | 周向 | 49.82 | 经向均布 | 50.20 | 经向近似均布 | 55.42 | φ=90° |
| 一次弯曲应力 | 周向 | 118.04 | φ=±43° | 111.57 | φ=±42.1° | 118.35 | φ=42.5° |
| 二次弯曲应力 | 经向 | 208.36 | φ=0°内、外壁面 | 236.59 | φ=-90°内壁面 | 246.82 | φ=-90°内壁面 |
| 注:①表中理论值依据弯管分析一次近似解并考虑压力弯矩共同作用的修正系数计算得到;②表中“—”表示理论上难以精确计算。 | |||||||
4 结 论
(1) 提出了一种新的弯管建模方法。利用该方法所建立的不均匀壁厚弯管有限元模型,同时考虑了弯管壁厚的经向不均匀性与周向不均匀性,解决了弯管模型壁厚不连续引起的附加边缘应力问题,模拟结果更加准确,可以用于弯管设计制造和安全评价分析。
(2) 建立了内压与弯矩联合作用下不均匀壁厚弯管的有限元模型。从更深层次分析可知,不均匀壁厚对弯管薄膜应力的分布有较大影响,适当的壁厚不均匀性有利于增强弯管承受内压的能力。
(3) 对于弯矩作用下的弯管,最大经向二次弯曲应力的校核对保证弯管的强度和寿命至关重要。对于不均匀壁厚弯管,强度校核时,应适当增大经向和周向的弯曲应力增强系数。
| [1] | 张足斌, 王海琴, 银永明. 油气管道与储罐设计[M]. 东营: 中国石油大学出版社, 2012 : 46 -68. |
| [2] | 徐思浩. 90°管弯头的应力分布[J]. 化工设备与管道, 2001, 38 (4) : 38–39 . |
| [3] | 孙兰萍, 赵建平. 不等厚性对弯头应力分布影响的有限元研究[J]. 南京工业大学学报(自然科学版), 2006, 28 (3) : 49–52 . |
| [4] | 段志祥, 沈士明. 平面闭合弯矩作用下弯管塑性极限载荷分析与试验[J]. 石油化工设备, 2005 (2) : 8–10 . |
| [5] | 张惠民. 输气管道中焊缝钢制弯管的试验研究[J]. 油气储运, 2004, 23 (10) : 36–39 . |
| [6] | DONG J H, BAO X F, ZHENG X Z. Comparison of two methods of finite element modeling for elbows with unequal wall thickness[J]. Physics Procedia, 2012, 33 :498–504 . |
| [7] | 修荣荣, 徐明海, 黄善波. 自动生成四边形网格的方法及其在数值模拟中的应用[J]. 中国石油大学学报(自然科学版), 2011, 35 (2) : 131–136 . |
| [8] | 王瑞, 陈海霞, 王广峰. ANSYS有限元网格划分浅析[J]. 天津工业大学学报, 2002, 21 (4) : 8–11 . |
| [9] | 段志祥, 沈士明. 内压作用下局部减薄弯管塑性极限载荷分析与试验研究[J]. 压力容器, 2005, 22 (5) : 1–3 . |
| [10] | 潘园稚.基于ANSYS的机翼机身对接接头非线性有限元分析[D].哈尔滨:哈尔滨工业大学,2013:34-35. |
| [11] | 陈孙艺, 柳曾典. 内压作用下弯管环向应力解及其分析[J]. 压力容器, 2006, 23 (2) : 38–41 . |
| [12] | 徐方成, 蒋家羚, 林兴华, 等. 内压作用下弯管应力的实验研究[J]. 厦门大学学报(自然科学版), 2000, 39 (5) : 617–621 . |



