2. 中国石油集团海洋工程有限公司工程设计院
2. CNPC Offshore Engineering Company Limited
0 引 言
柔性接头广泛应用在深水立管系统中,在连接立管和上部浮体的同时还可以增强连接部位的强度,抵抗浮体运动。柔性接头所处的环境复杂(风、浪、流、高温高压和腐蚀等),其关键部件弹性体易产生疲劳损伤。2004年5月,矿物管理局报导墨西哥湾TLP平台外输SCR柔性节点发生泄漏,泄漏检查发现平台的输油和输气柔性节点均存在可见性损伤[1]。因此,开展柔性接头疲劳特性相关研究对掌握其关键技术和打破国外技术垄断具有重要意义。
周灿丰等[2]研究了深水立管系统柔性接头的应用场合、关键构件及安装原则等基本技术问题,并分析了轴向张力、介质压力、偏角、转动刚度和尺寸等因素对柔性接头选型的影响。刘培林等[3]结合南海“荔湾3-1”深水油气田的环境特征,采用ABAQUS有限元软件对其进行了非线性分析及强度校核。K.G.HANNUS[4]分析了柔性接头在轴向张力和弯矩联合作用下钢筋夹层的应力分布情况,并与全尺寸试验结果进行对比分析。李成钢等[5]对比分析了3种不同类型的柔性接头的适用范围及设计要求,并分析了柔性接头的插座、防护罩和运输工具等系列附件性能。郑辉等[6]对钢悬链线立管进行了时域动力分析,提取立管顶端局部响应的时域谱作为柔性接头非线性分析的载荷谱,最后采用fe-safe软件对其疲劳寿命进行预测。JIN X等[7]对柔性接头在中国南海荔湾油田使用中的疲劳寿命进行预测。R.H.GUNDERSON等[8-9]采用断裂力学的方法分析了在机械载荷及橡胶老化效应的共同作用下,柔性接头弹性体的疲劳寿命,同时结合断裂力学与疲劳失效判断准则分析柔性接头的疲劳寿命,并测量柔性接头试样疲劳试验后的裂纹扩展情况。以上研究均未考虑温度对柔性接头疲劳特性的影响。为此,笔者分析了柔性接头在不同温度条件下的疲劳特性,所得结果对柔性接头的设计和使用具有指导意义。
1 深水钢悬链线立管非线性分析 1.1 有限元模型深水钢悬链线立管在位时呈现大变形状态,具有几何非线性特性,这给其有限元分析带来了困难。
笔者采用有限元软件ABAQUS建立深水钢悬链线立管有限元模型,立管采用梁单元B31来模拟,将海床定义为离散刚体。立管与海床之间定义接触,且摩擦因数为0.4。立管的初始状态定义为平铺在海床上,并通过在立管一端施加位移载荷将其提升至在位状态。为保证提升过程计算的收敛性,将此过程分为6个分析步完成。立管提升至在位状态后,利用船体运动幅值响应算子(Response Amplitude Operator,RAO)在立管顶端施加船体运动边界条件,定义纵荡RAO为1.30×10-1、横荡RAO为7.76×10-5、垂荡RAO为1.57×10-1。海流和波浪载荷通过AQUA模块加载。
建模时立管外径308.4 mm,壁厚30.84 mm,弹性模量208 GPa,泊松比0.3,密度7 850 kg/m3。立管所处的海洋环境参数为:波高3.5 m,波浪周期6.4 s,表面流速1.37 m/s,底面流速0.00 m/s,水深3 000 m,海水密度1 025 kg/m3。
1.2 有限元计算结果分析由于立管重力引起的张力作用使得钢悬链线立管在靠近顶端时应力逐渐增大,所以柔性接头工作时承受较大的应力,如图 1所示。
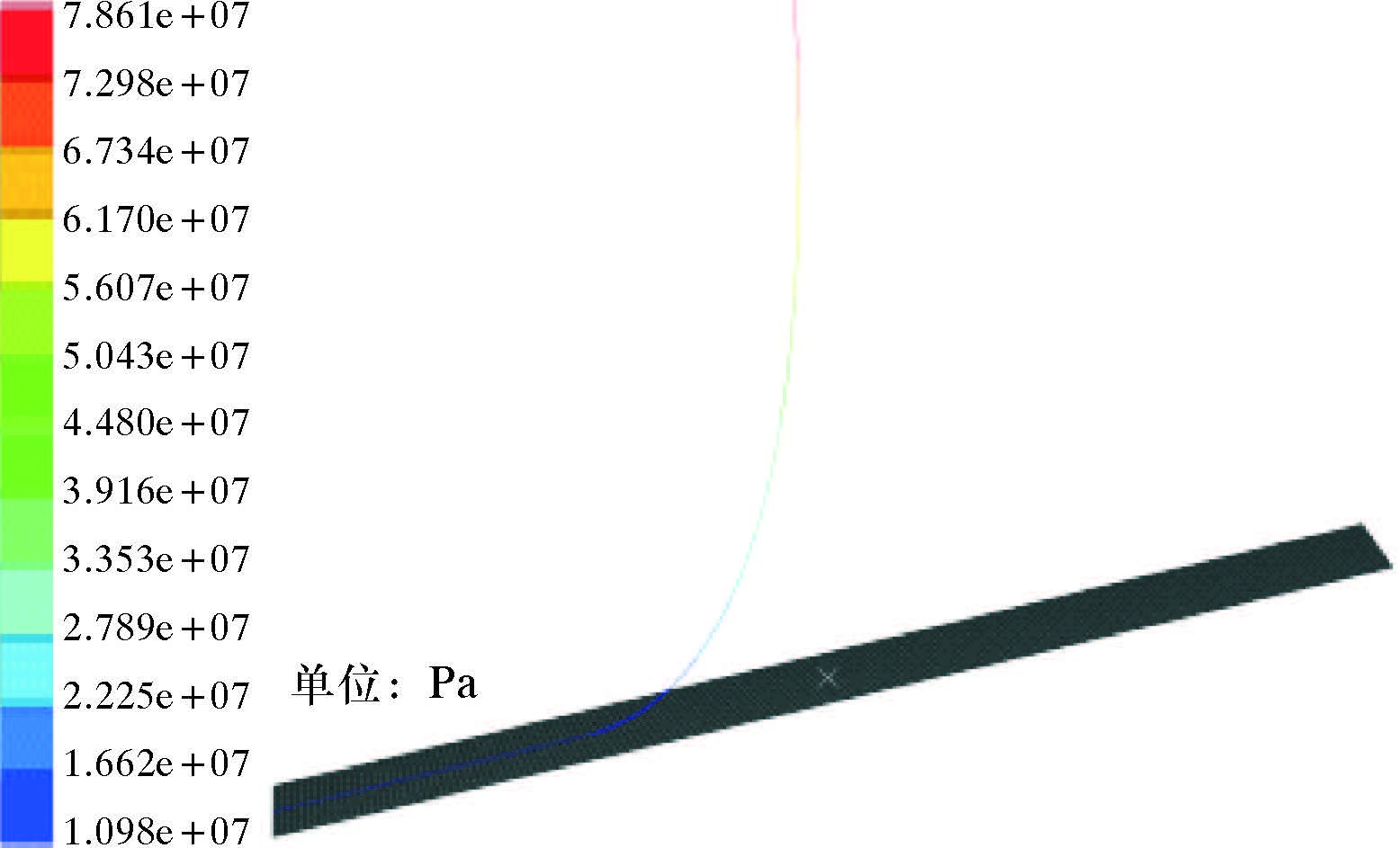
|
| 图 1 柔性接头工作时承受的应力云图 Fig.1 The stress distribution of flexjoint under working condition |
提取水面上1 m处立管截面的轴力和弯矩时间-历程曲线作为柔性接头有限元计算的边界条件,如图 2所示。
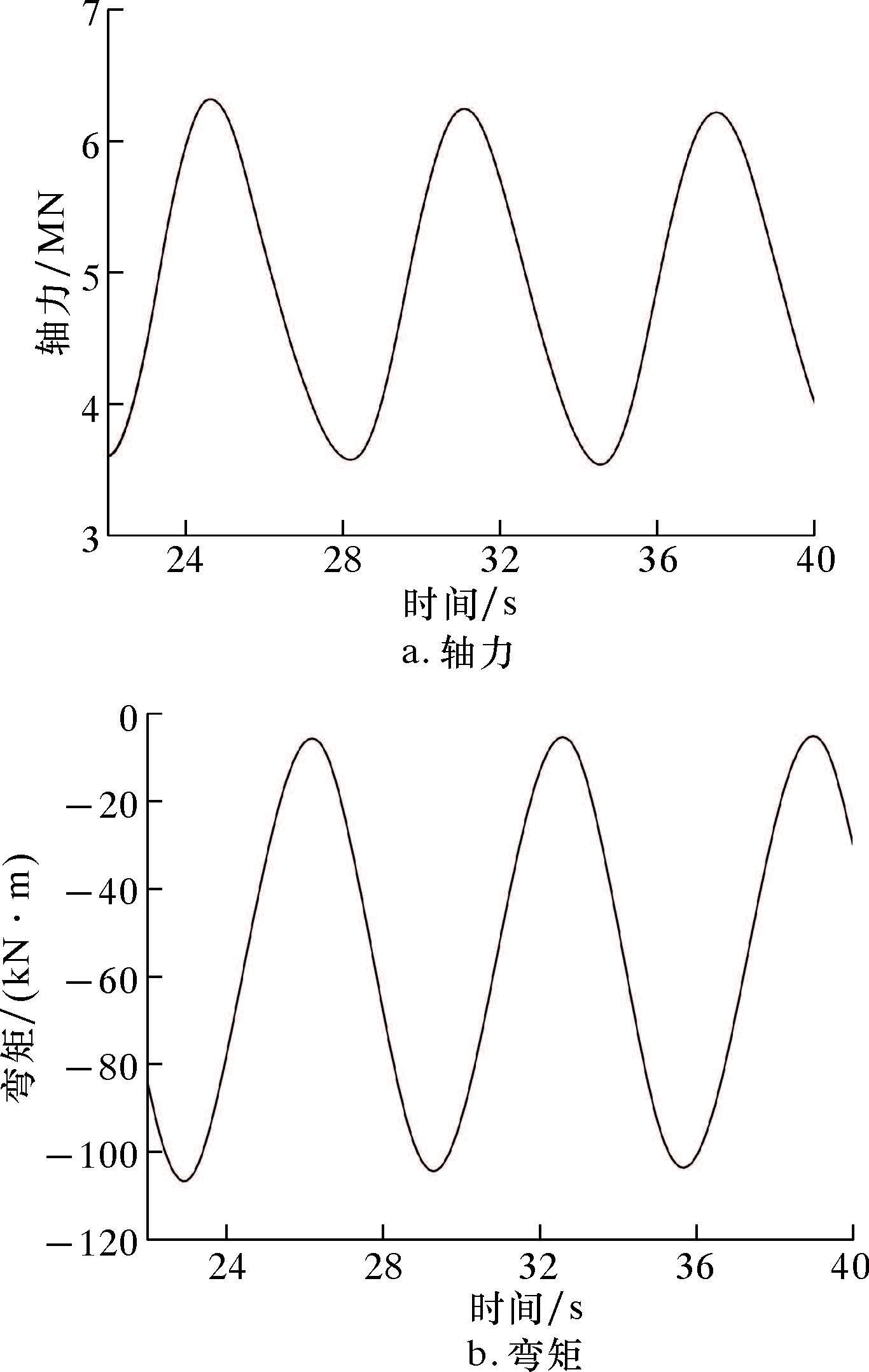
|
| 图 2 水面上1 m处立管截面轴力和弯矩时间-历程曲线 Fig.2 Time history of axial force and moment of riser section 1 m above water |
2 柔性接头非线性有限元分析 2.1 柔性接头有限元模型
柔性接头中的橡胶元件是易损元件,因此柔性接头疲劳特性分析的重点为橡胶元件。如图 3所示,柔性接头有限元模型包含3个部分:主体、延伸件和弹性体。为了减少计算工作量,对有限元模型进行适当简化,主体与延伸件均定义为离散刚体,且与弹性体的连接界面为理想界面。弹性体采用实体单元C3D8R模拟,橡胶元件单元数为6 000个,钢筋夹层单元数为5 800个。在延伸件下端定义参考点,与延伸件最下端截面耦合在一起,施加轴向力和弯矩。
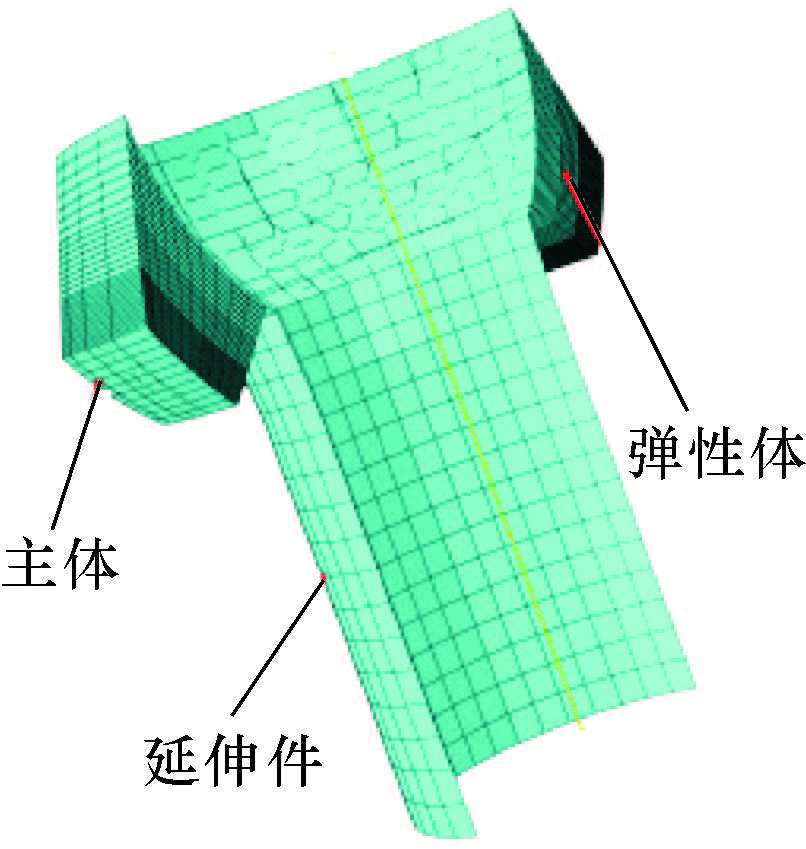
|
| 图 3 柔性接头有限元模型 Fig.3 Finite element model of flexjoint |
2.2 材料属性定义
橡胶属于超弹性材料,其力学性能非常复杂,受环境温度、加载速率和应变历史等因素的影响,在大应变条件下不能简单地用弹性模量来描述其变形性能。为此,研究人员提出了很多的橡胶本构模型,如Mooney-Rivlin模型、Ogden模型和Neo-Hookean模型[10]。其中,常用的橡胶模型是Mooney-Rivlin模型。公式(1)为2参数的Mooney-Rivlin模型。
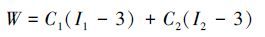 (1)
(1) 式中:W为应变能函数,I1和I2分别是第1、第2应变不变量,C1和C2为与温度相关的常数,取值见参考文献[11]。
表 1为不同温度下热膨胀系数α的取值。在40~140 ℃的温度范围内,钢筋夹层材料的性能参数变化很小,可以用一个常数值。
定义钢筋夹层的弹性模量为208 GPa,泊松比0.3,热膨胀系数1.22×10-5/℃。
| 温度/℃ | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 |
| α/(10-4-1) | 1.25 | 1.68 | 2.04 | 2.35 | 2.60 | 2.78 | 2.90 | 2.97 | 2.97 | 2.92 | 2.80 |
2.3 橡胶元件非线性有限元分析
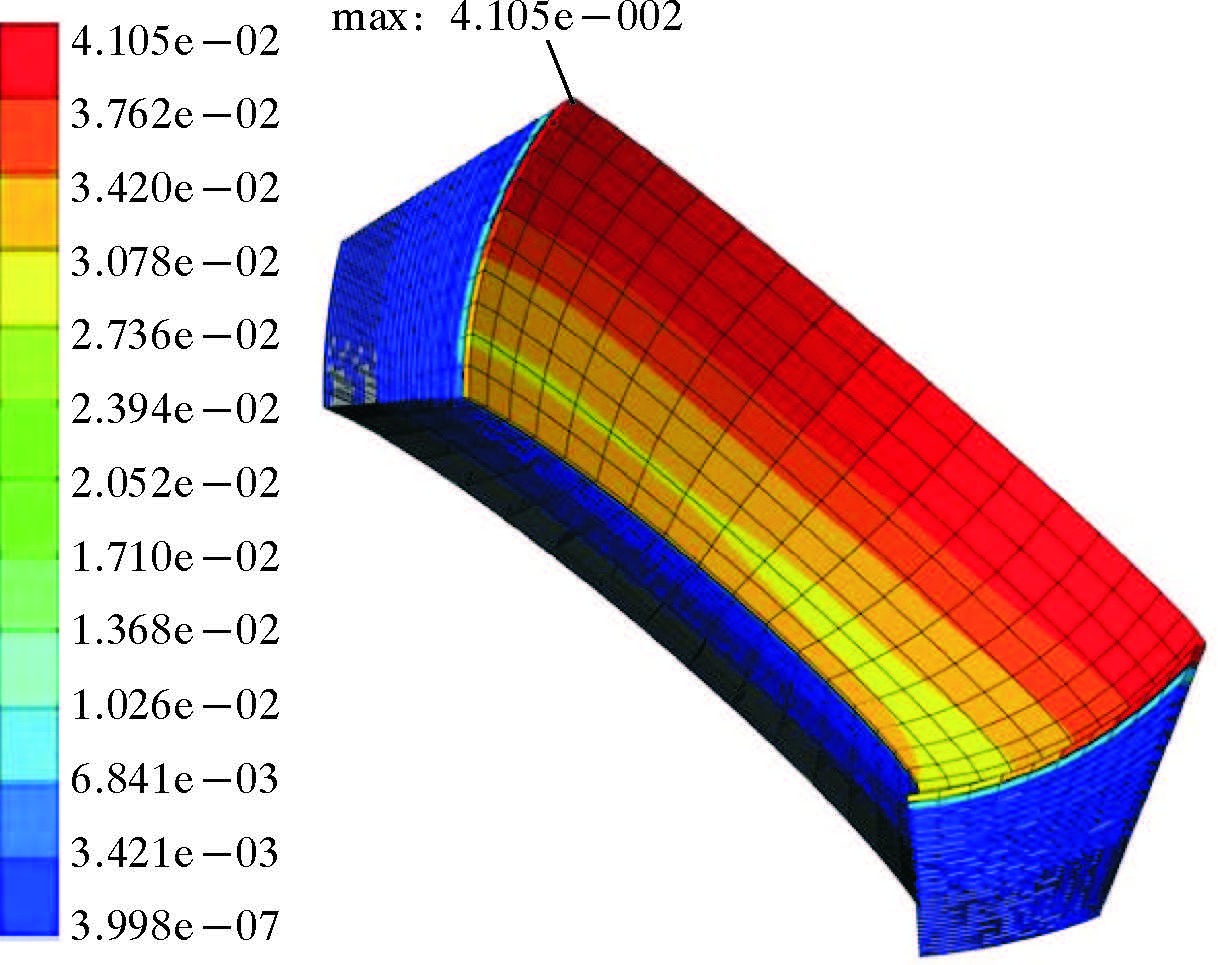
将轴力和弯矩的时间-历程曲线作为边界条件施加在柔性接头有限元模型的参考点处。通过预定义温度场来施加不同的温度场,分析橡胶元件不同温度条件下的应变变化规律。预定义温度场为40 ℃时,柔性接头橡胶元件中最上层橡胶的应变最大,如图 4所示。
|
| 图 4 柔性接头橡胶元件应变云图 Fig.4 The strain distribution of flexjoint rubber element |
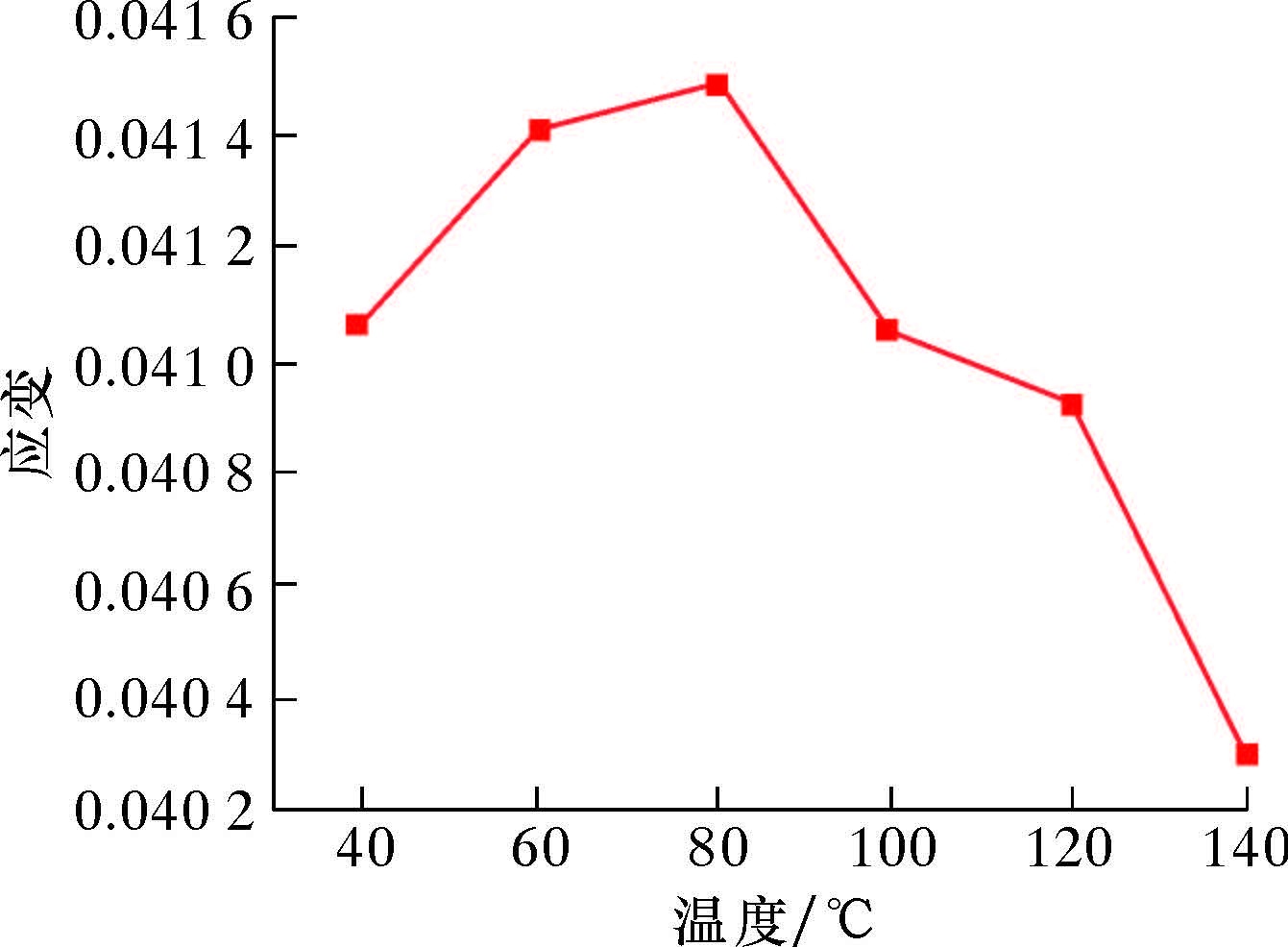
弯矩作用最大应变发生在橡胶一端,最大值为4.105×10-2。由于不同温度条件下橡胶的本构关系不同,使得橡胶元件的最大应变随着温度的变化而变化,如图 5所示。由图可知,当温度场由40 ℃变为80 ℃时,橡胶元件的最大应变逐渐增大,在80 ℃时达到最大值;当温度场由80 ℃变为140 ℃时,橡胶元件的最大应变逐渐减小。
|
| 图 5 不同温度下橡胶元件应变变化规律 Fig.5 The rubber element strain variation under different temperatures |
3 柔性接头橡胶元件疲劳寿命预测
橡胶材料的疲劳寿命预测主要有3种方法:等效应变法、等效应力法和能量法。余伟炜[12]采用现有疲劳寿命预测方法对橡胶材料进行疲劳寿命预测,并对预测的效果进行对比分析,其中等效应变法预测的疲劳寿命与试验数据拟合效果良好,又因其计算简单被广泛应用。等效应变法建立疲劳损伤参量与橡胶疲劳寿命的关系为:
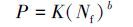 (2)
(2) 式中:Nf为橡胶完全断裂时的疲劳循环次数;K和b分别为材料常数;P为疲劳损伤参量。
在等效应变法中可选择最大主应变峰值,最大主应变量包括Green-Lagrange应变、Almansi-Euler应变、对数应变及工程应变等。笔者选择最大工程应变作为疲劳损伤参量,其中K=59.24,b=-0.34[13]。
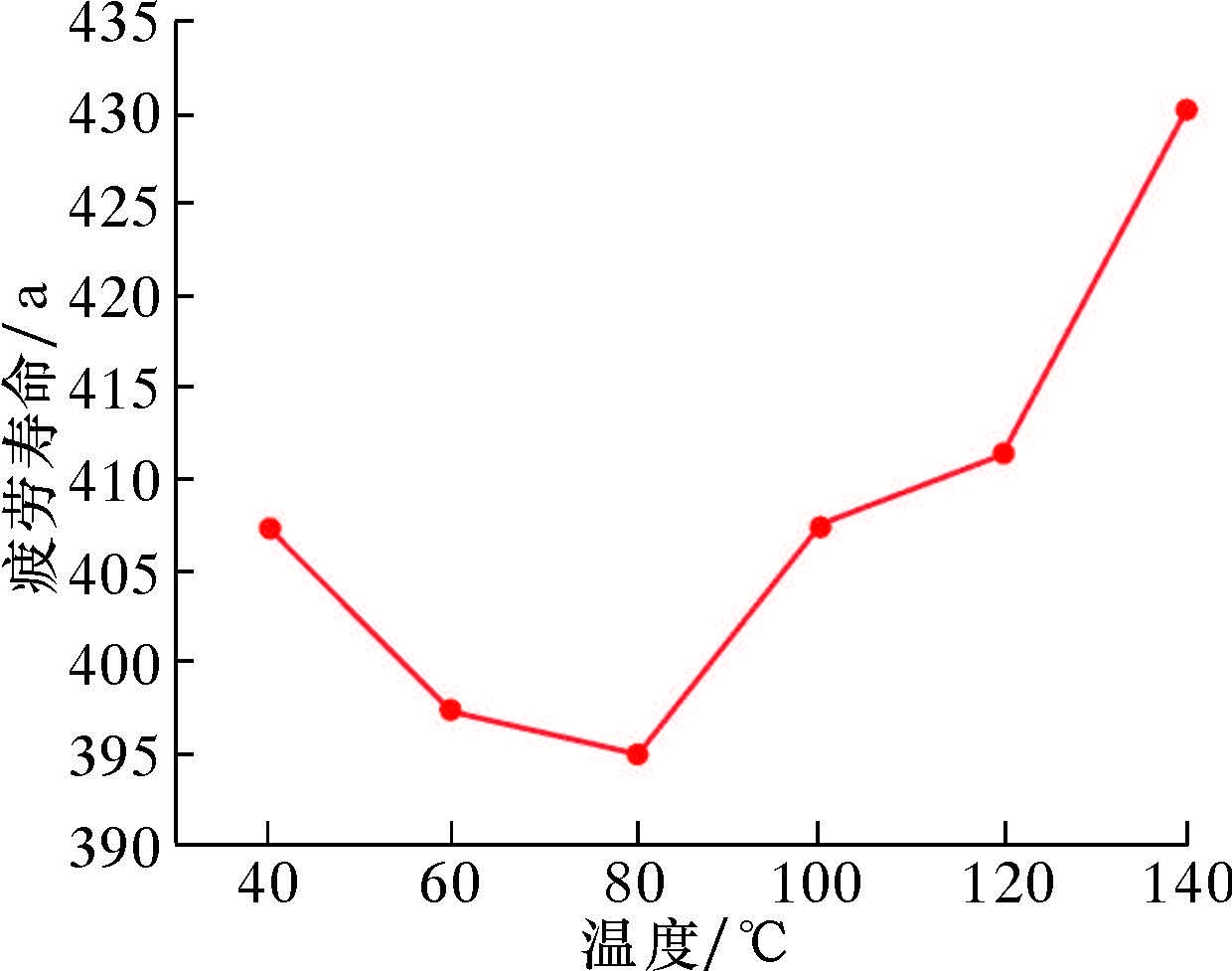
将2.3节计算出的不同温度下橡胶元件的最大工程应变代入公式(2)中,计算出橡胶元件完全断裂时的疲劳循环次数Nf,再根据循环周期为6.4s最终计算出柔性接头橡胶元件的疲劳寿命,如图 6所示。由图可知,当温度场在40~80 ℃区间时,橡胶元件疲劳寿命逐渐缩短,在80 ℃时达到最小值;当温度场在80~140 ℃区间时,橡胶元件的疲劳寿命逐渐延长。
|
| 图 6 不同温度下橡胶元件疲劳寿命变化曲线 Fig.6 The fatigue life of rubber element at different temperatures |
4 结 论
(1)柔性接头橡胶元件的最大应变发生在最上层橡胶的一端,因此在设计时应增强第1层橡胶的强度,以延长柔性接头的使用寿命。
(2)当温度场在80 ℃时橡胶元件疲劳寿命最短,因此在设计和使用柔性接头时应避免橡胶元件处在这一温度场范围内。
| [1] | MANSOUR G. Deepwater riser design, fatigue life and standards study report[M]. Washington: Minerals Management Service, 2007 . |
| [2] | 周灿丰, 焦向东, 曹静, 等. 深水立管柔性节点选型设计研究[J]. 北京石油化工学院学报, 2012, 20 (1) : 30–33 . |
| [3] | 刘培林, 金鑫, 段梦兰, 等. 深水立管顶端柔性节点设计及非线性分析[J]. 中国海洋平台, 2012, 27 (5) : 12–15 . |
| [4] | HANNUS K G. A flexelement analysis[R].OTC 6581,1991. |
| [5] | 李成钢, 金鑫, 张敬安, 等. 深水立管顶端柔性节点结构设计[J]. 石油矿场机械, 2013, 42 (7) : 38–42 . |
| [6] | 郑辉, 金鑫, 李成钢, 等. 深水立管顶端柔性节点疲劳寿命预测[J]. 海洋技术, 2013, 32 (4) : 99–103 . |
| [7] | JIN X,ZHANG J A,LI C G,et al.Fatigue life prediction for flexible joint of deepwater riser in liwan gasfield of the South China Sea[C]//Proceedings of the Twenty-fourth (2014) International Ocean and Polar Engineering Conference Busan.Korea,2014:230-234. |
| [8] | GUNDERSON R H,STEVENSON A.Ageing and fatig- ue life of structural TLP flexelements[R].OTC 8517,1997. |
| [9] | GUNDERSON R H,STEVENSON A,HARRIS J A, et al.Fatigue life of TLP flexelements[R].OTC 6898,1992. |
| [10] | 徐立, 吴桂忠. 有限元分析中橡胶应变能函数的若干形式[J]. 橡胶工业, 1999, 46 (12) : 707–711 . |
| [11] | 方庆红.纤维增强橡胶在不同温度条件下的力学性能研究[D].沈阳:东北大学,2006. |
| [12] | 余伟炜.橡胶材料多轴疲劳寿命研究[D].天津:天津大学,2007. |
| [13] | 王小莉.橡胶隔振器多轴疲劳寿命预测方法研究[D].广州:华南理工大学,2014. |



