0 引 言
海洋工程普遍采用圆柱形断面结构物,当海流流经这些圆柱形结构物后,其后方会产生周期性的交替泄涡,交替泄涡会产生较大的升力波动。对于弹性支撑或者细长柔性结构,这种升力波动产生的涡激振动会大大影响结构物的寿命,因此在海洋结构物设计时必须对涡激振动的影响加以考虑。近年来,学者们研究了多种涡激振动抑制装置。
目前,涡激振动抑制装置主要为螺旋列板、导流板、分隔器以及附属杆。L.LEE等[1]通过试验研究了导流板的阻尼特性,结果发现,导流不但可以对涡激振动起到抑制效果,而且会产生额外的水动力阻尼,这对波浪载荷会产生一定的削减作用。G.R.S.ASSI等[2]通过试验研究了不同形式的导流板对涡激振动的抑制效果。近年来,更多的学者通过数值模拟技术研究了圆柱扰流及涡激振动的抑制。ZHAO MING等[3]针对不等径的双管进行了单向流固耦合数值模拟,研究了距离和角度对流体力的影响。H.SARVGHAD[4]通过数值模拟方法研究了并列管的数值扰流问题。鞠少栋等[5]针对螺旋列板涡激振动抑制装置进行了数值模拟。沙勇等[6]通过水池试验对螺旋列板的参数进行研究,发现螺距及覆盖率对螺旋列板的抑制效果影响很大。魏泽等[7]通过单向流固耦合数值模拟方法对螺旋侧板的抑制效果进行研究。徐枫等[8]通过数值模拟方法研究了行波壁对圆柱涡激振动的抑制效果。3根附属杆作为常用的立管涡激振动抑制装置被广泛应用,但是针对3根附属杆抑制机理的研究并不深入。笔者通过数值模拟的方法在不同来流角度及多个间隙比条件下,针对3根附属杆抑制装置对立管所受流体力的抑制效果、泄涡模式及抑制机理进行深入研究,以期为海洋立管的涡激振动抑制装置研究提供参考。
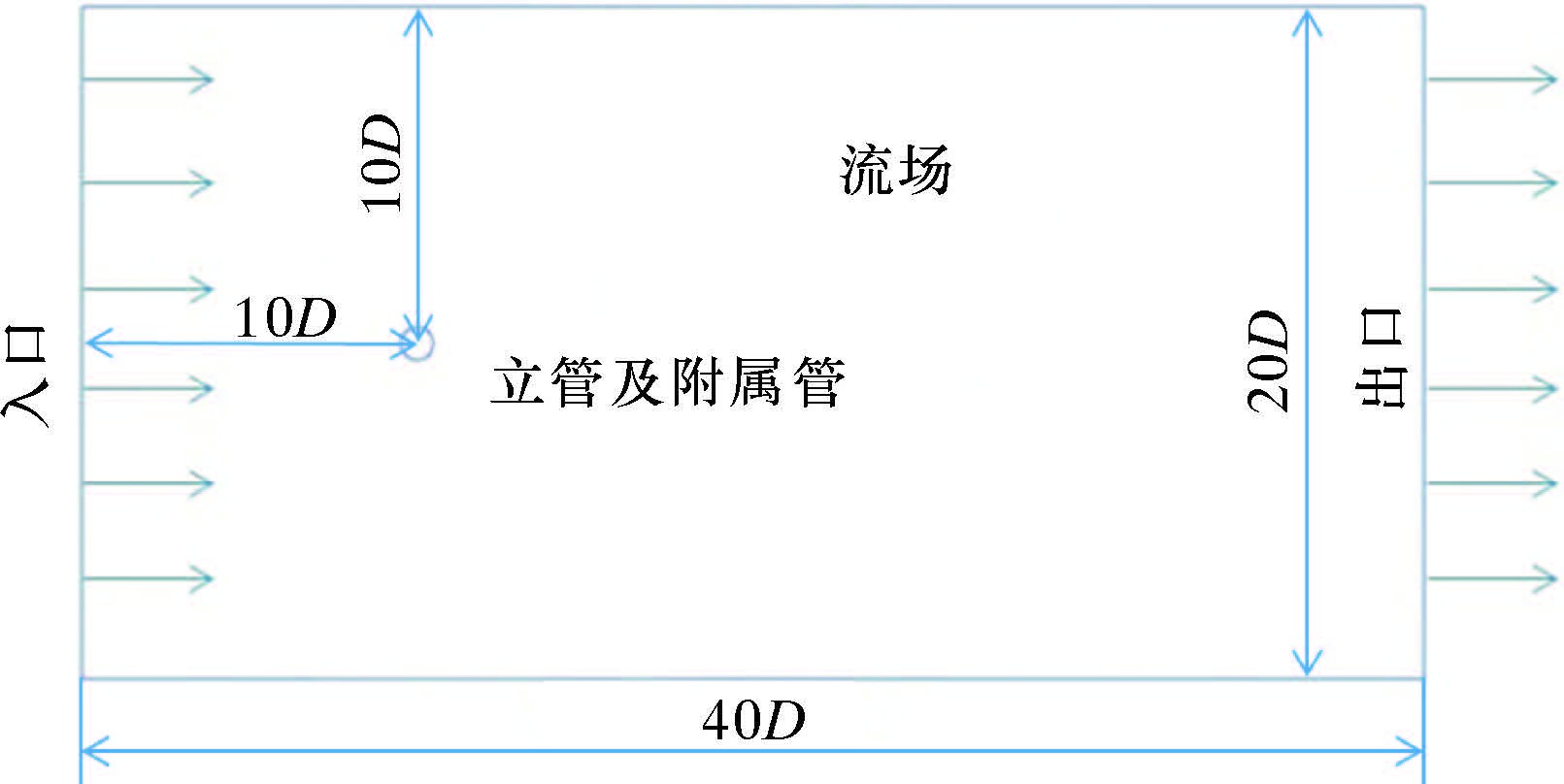
1 数值模型 1.1 数学模型计算域采用40D×20D的矩形流场。考虑入口端对立管的影响,流场入口距立管中心为10D;考虑尾流中的涡街不被出口边界影响,出口边界距离立管中心为30D;2横向边界距离立管中心均为10D。D为与来流方向垂直的特征长度,在文中D为立管直径。流场模型示意图如图 1所示。
|
| 图 1 流场模型示意图 Fig.1 Schematic of flow model |
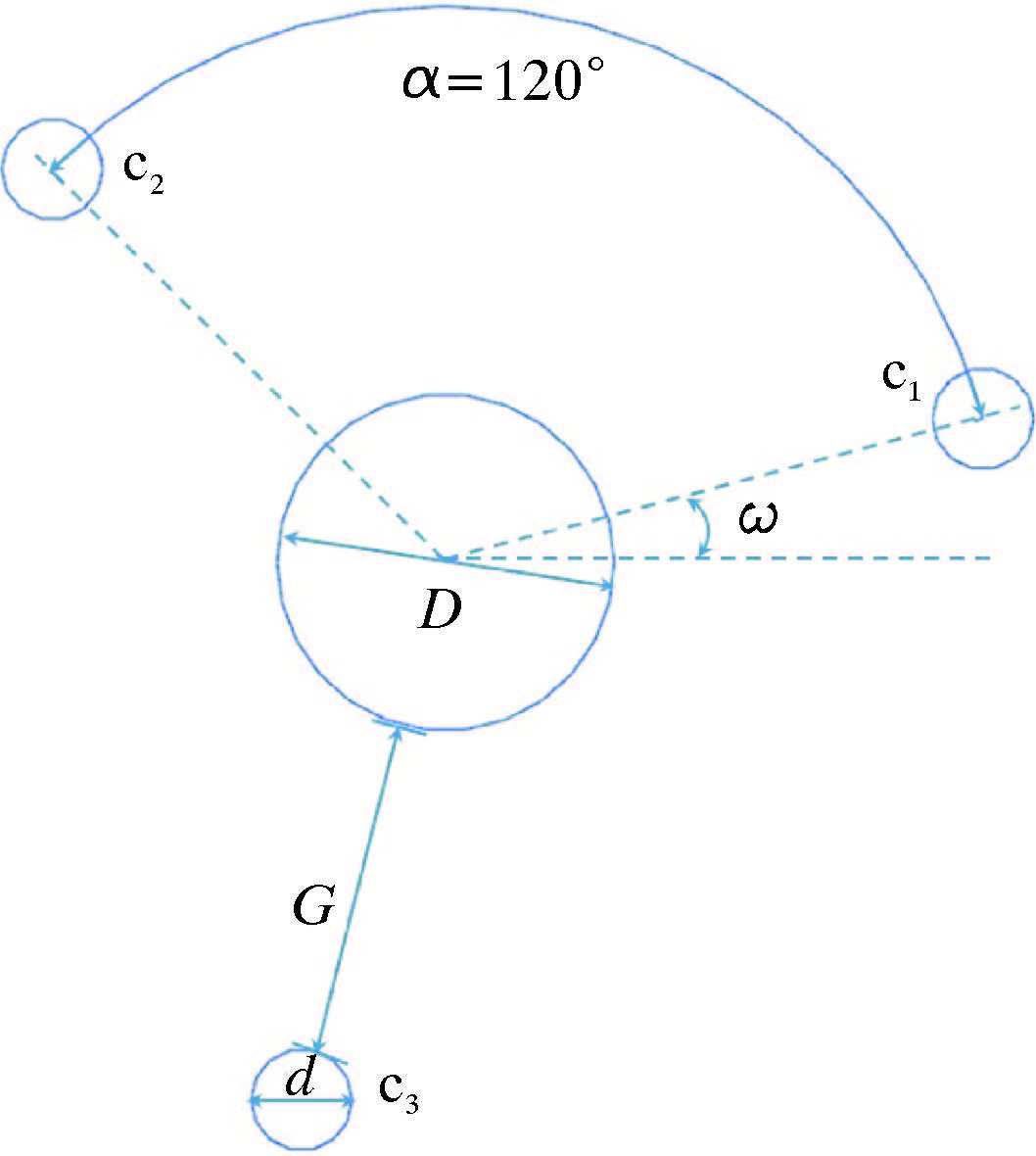
立管与附属管的位置关系如图 2所示。3根附属杆绕立管均匀布置,逆时针方向的3根附属杆依次为c1、c2、c3。
图中:D为立管直径,d为附属杆直径,ω为附属杆c1与X轴正向的夹角,ω=0~π/3,增量为π/12;α为2根附属杆之间的夹角,文中3根附属杆均匀布置在立管周围,α=120°。G为立管外壁与附属杆外壁之间的间距。
|
| 图 2 立管与附属管位置关系图 Fig.2 Positional relationship of riser and the control rod |
直角坐标系下,流体域的连续性方程和动量方程分别如下:
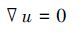 (1)
(1) 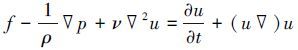 (2)
(2) 式中:ρ为流体密度;ν为流体运动的黏度系数;u为速度矢量;f为作用在单位质量流体上的质量力。
作用在立管上的升力系数CL与拖曳力系数CD分别为:
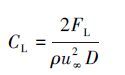 (3)
(3) 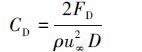 (4)
(4) 式中:FL为作用在立管上的升力,FD为作用在立管上的拖曳力,u∞为均匀来流流速。
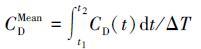 (5)
(5) 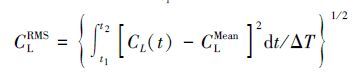 (6)
(6) 式中:CDMean为拖曳力系数均值,CLRMS为升力系数均方根值,ΔT为计算的时间步长,CMeanL为升力系数均值。
1.2 网格划分对整个流体域进行网格划分,网格的质量对计算精度和计算速度有很大影响,高精度会使结果更加准确,但当网格精度达到一定数量后,其对精度的影响有限。此时,过大的网格数量只会增加计算量,延长计算时间。
因此,应对网格数量进行合理控制。文中流体域网格总数为60万左右。为了保证计算的准确性,笔者对重要部分进行了网格加密。对于立管横流向和顺流向的方向,网格密度较高,因为立管前方是流体力作用的高压区,后方是涡街释放区,两侧是泄涡分离点。对立管周围建立边界层,以保证计算精度。图 3为近壁网格边界层。

|
| 图 3 近壁网格边界层 Fig.3 Near-wall mesh boundary layer |
2 结果分析 2.1 流体力分析
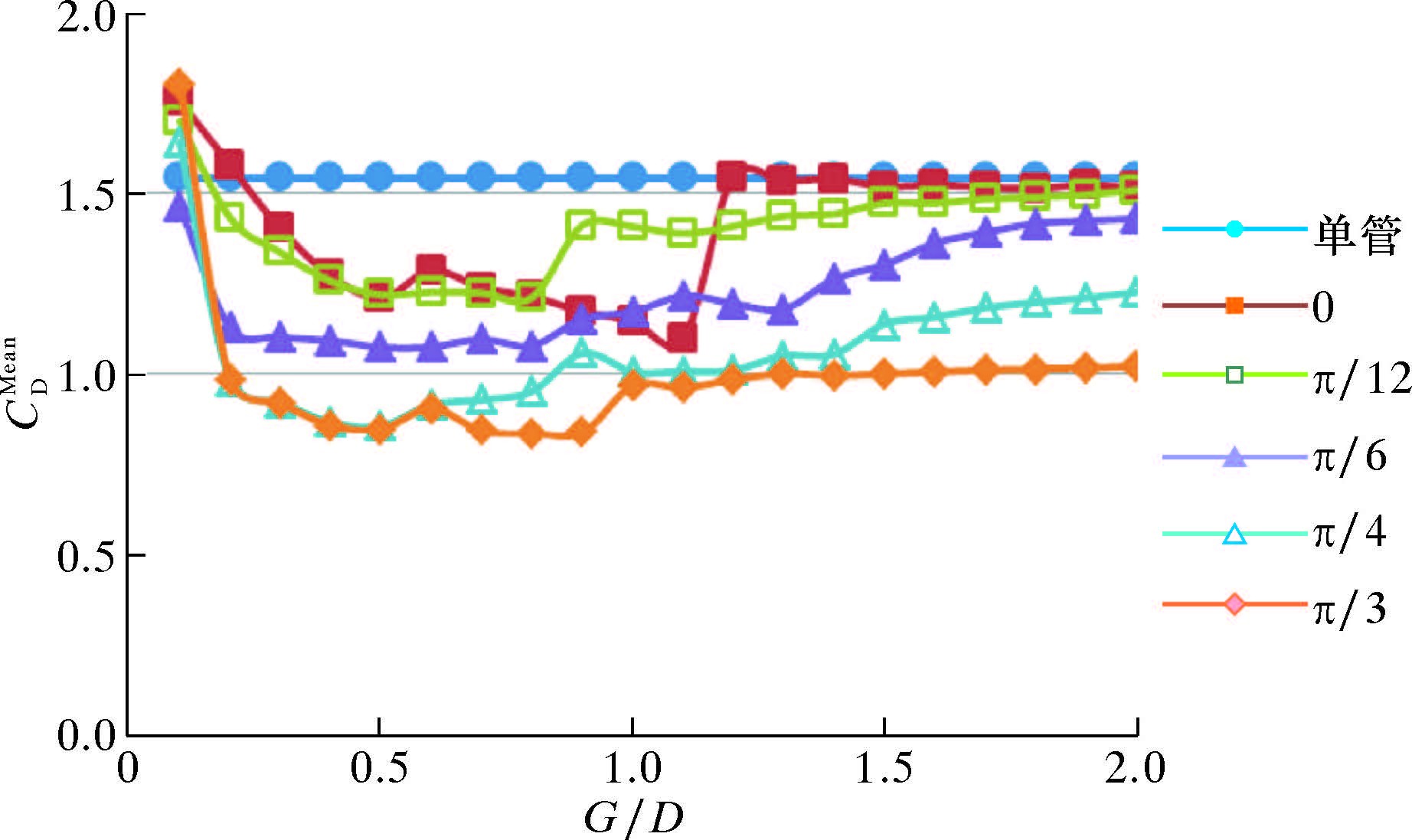
本节主要研究不同来流角度及间隙比条件下,附属杆对立管所受拖曳力系数均值CDMean和升力系数均方根值CLRMS的抑制效果。图 4和图 5分别为CDMean和CLRMS随ω变化的曲线。拖曳力系数方向与流场方向相同,代表立管受到流体顺流向的作用力。升力系数代表立管受到的垂直于流体流向的作用力。由图 4和图 5可知,来流角度ω和间隙比G/D对立管拖曳力系数均值和升力系数均方根值的影响较大。
|
| 图 4 立管CDMean随ω变化曲线 Fig.4 The effect of ω on riser CDMean |
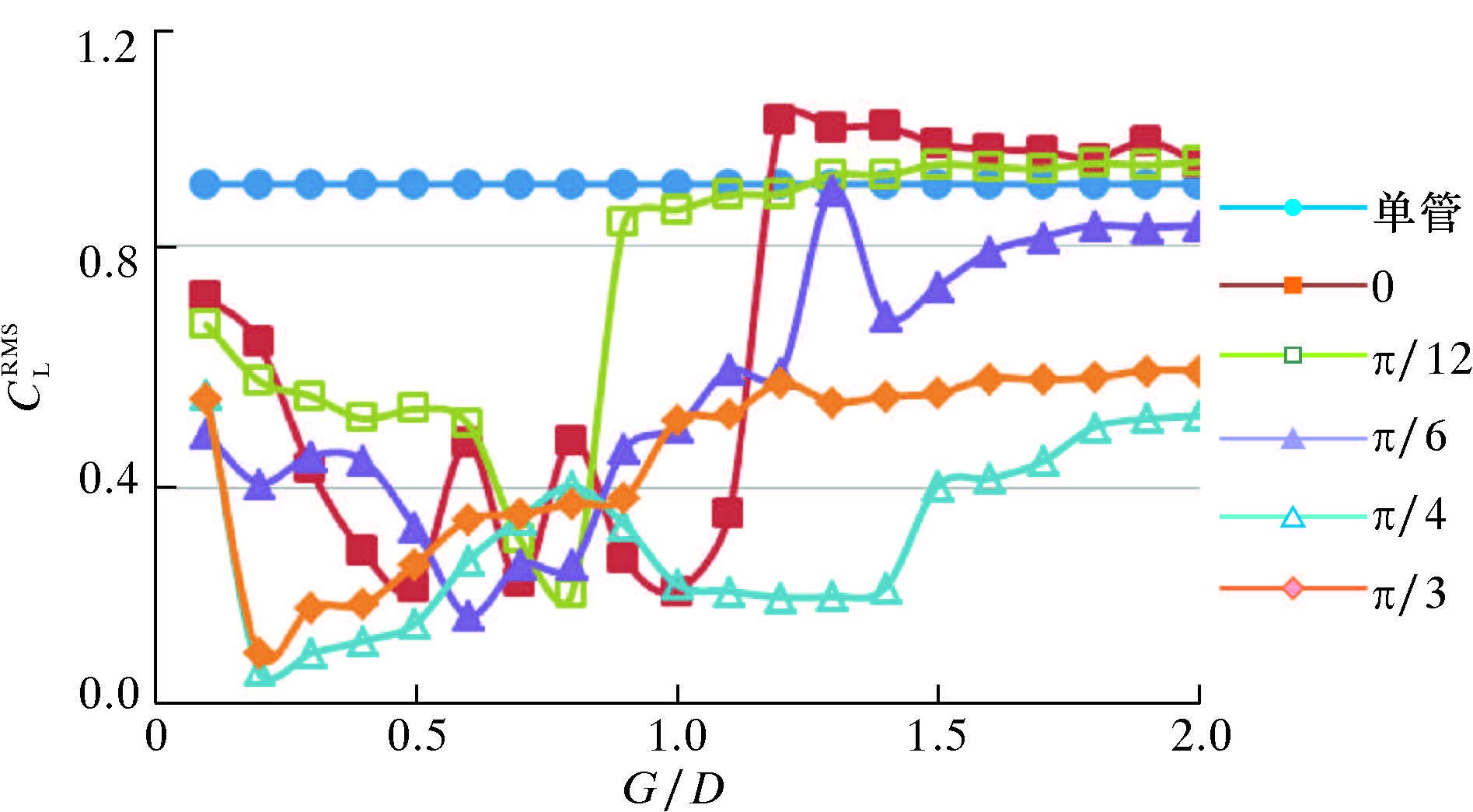
当ω=0、G/D=0.4~1.1时,对升力系数均方根值CLRMS抑制效果较好,抑制效果维持在70%左右,当G/D=1.0时抑制率为75%。
当ω=π/12、G/D=0.7~0.8时,对升力系数均方根值CLRMS有较好的抑制效果。当G/D=0.8时,对升力系数均方根值的抑制率为75%,达到此来流角度下抑制效果的最大值;而当G/D=0.9时,抑制效果仅为7%,几乎没有抑制效果,并且随着G/D的增大CLRMS略有增大,说明当G/D=0.8~0.9时CLRMS对间隙比十分敏感。
|
| 图 5 立管CLRMS随ω的变化曲线 Fig.5 The effect of ω on riser CLRMS |
当ω=π/6、G/D=0.6时,对CLRMS抑制率达到最大值79%;当G/D=0.5~1.0时,对CLRMS有较好的抑制效果。
当ω=π/4、G/D=0.2时,对升力系数均方根值CLRMS抑制效果最好,抑制率达到89%。在G/D=0.2~1.4范围内,抑制效果较好,抑制率超过70%,有效抑制区间最宽。
当ω=π/3、G/D=0.2~0.7时,抑制效果较好,抑制率超过为60%,对立管CLRMS的抑制率最高达到 86%。在G/D=0.8~2.0范围内,抑制效果持续存在,此时随着G/D的增大,抑制效果逐渐下降。当G/D>1.0后,抑制效果基本保持不变,抑制率保持在40%左右。
从各来流角度对CLRMS的抑制效果可以看出,对于不同的来流角度,3根附属杆在不同的间隙比下抑制效果不同,ω=0、π/6及π/3时,在较宽的范围内对立管CLRMS的抑制率都超过70%。而当ω=π/12和π/4时,抑制区间有限,仅在较窄的间隙比区间内有较好的抑制效果。综合来流角度及间隙比的影响,为了保证3根附属杆在各来流角度下对立管均有较好的抑制效果,间隙比G/D应在0.6~0.8之间为宜。
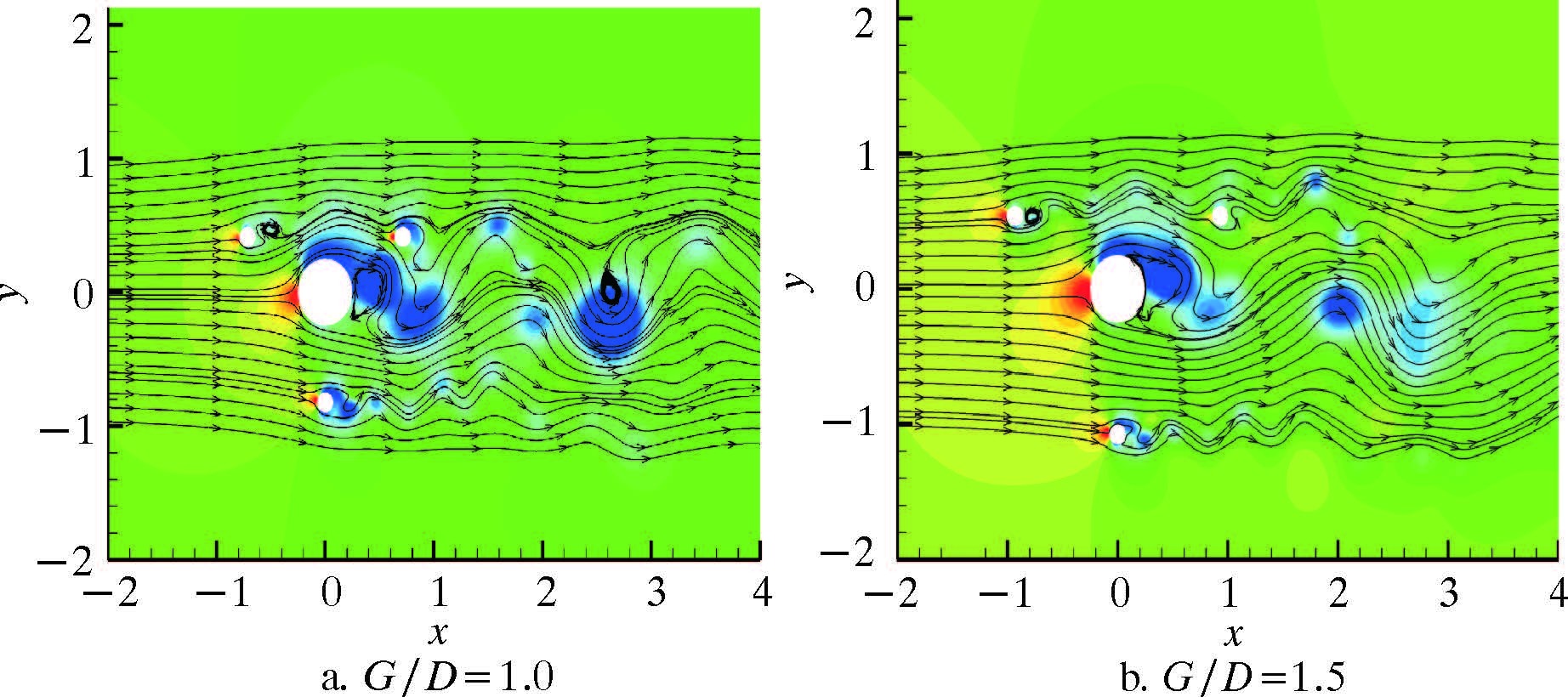
2.2 压力场分析立管附近的压力场能够直接反映立管周围的压力变化。压力的变化是导致拖曳力系数和升力系数变化的直接因素,因此本节主要分析带有附属管的立管系统在5种来流角度下压力场的变化规律。图 6~图 10分别为不同来流角度下,附属杆及立管周围压力场分布图。图中纵横坐标均为无量纲的压力场方向。G/D=0.1为附属管与立管距离最近的位置,此时CLRMS抑制效果较差且CDMean比单根立管时要大;G/D=0.7时,5种来流角度下均有较好的抑制效果;而当G/D=1.0时,某些来流角度下附属杆对立管的CLRMS抑制效果较差,而其他角度仍有较好的抑制效果,属于对来流角度较为敏感的间隙比;G/D=1.5时附属杆距离立管较远。从图 4和图 5可以看出,在此位置后,对于固定的来流角度,随着G/D的增大,立管上的流体力系数变化较小。但不同来流角度下立管受到的流体力仍然存在差异。
|
| 图 6 ω=0时附属杆及立管周围压力场分布 Fig.6 The pressure distribution around the |
|
| 图 7 ω=π/12时附属杆及立管周围压力场分布 Fig.7 The pressure distribution around the |
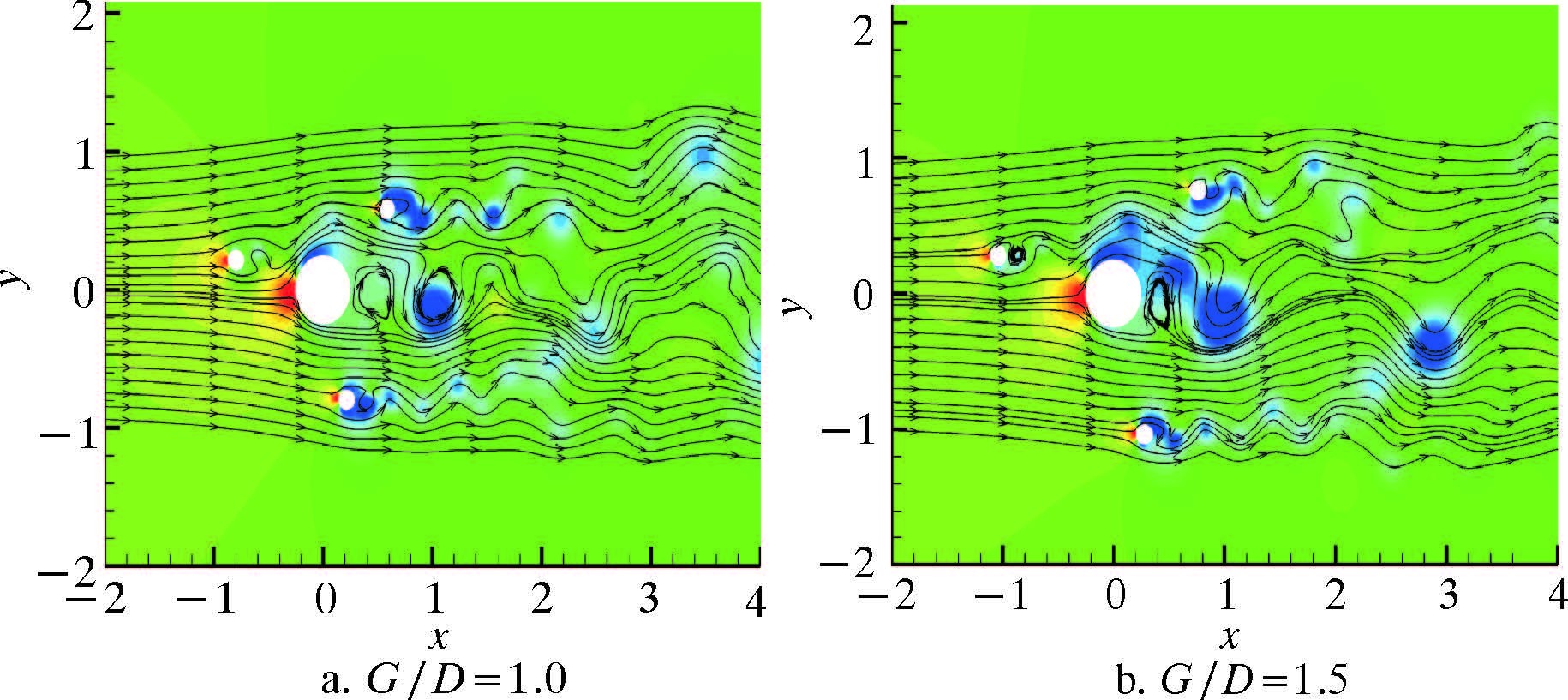
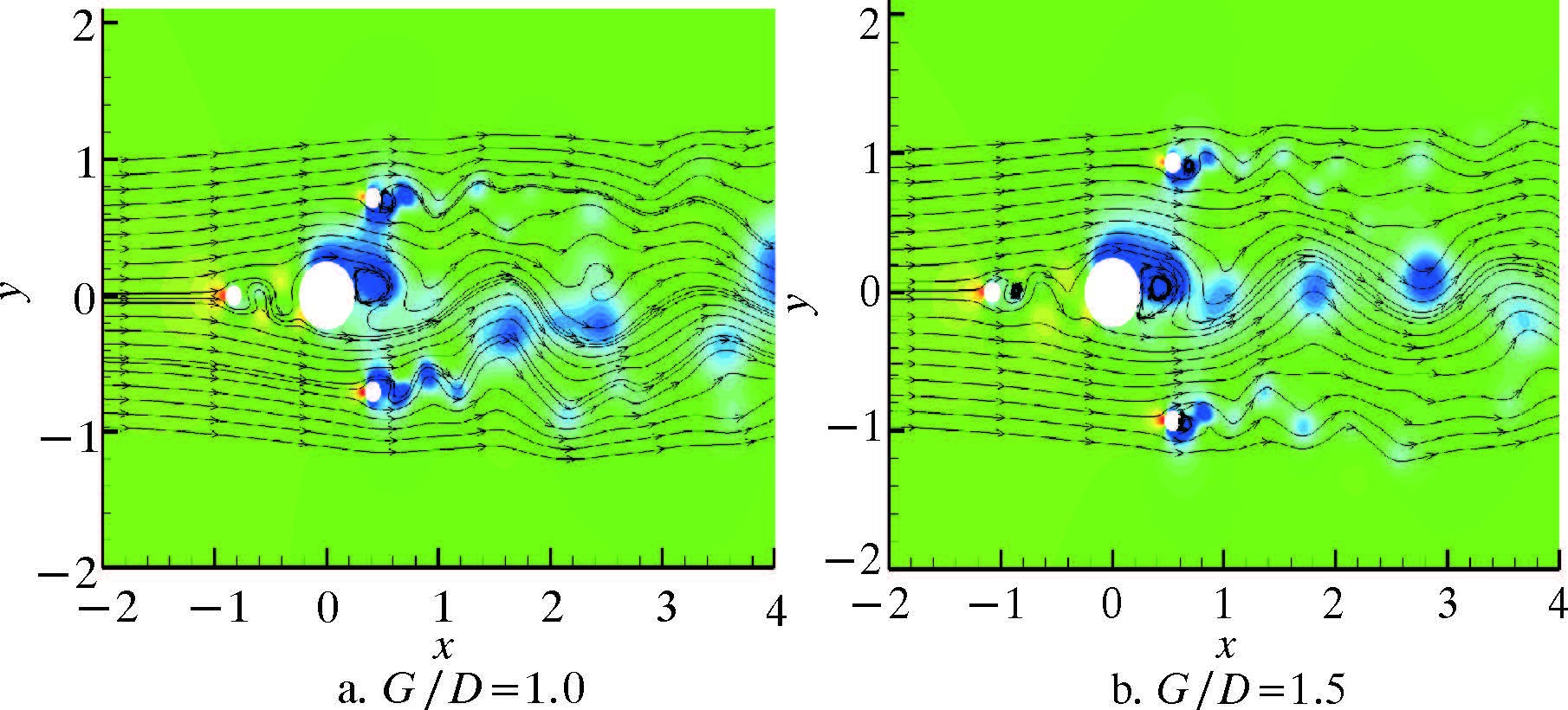
由分析可知,当G/D=0.1时,各角度下的压力场比较相似,立管前方均存在高压区,且立管两侧的压力差较大。因为此时的附属杆距离立管过近相当于增加了立管的有效直径,所以立管周围的压力分布几乎没有改变。当G/D=0.7时,带有附属杆的立管在各来流角度下的压力场表现略有差异。可以看到,随着来流角度ω的增大,立管前方的高压区越来越弱,而后方的低压区压力逐渐上升,导致前、后压力差降低,进而导致CDMean随着ω的增大逐渐降低。但可以看到此刻各角度下立管上、下两侧的低压区差别明显减小,压力差小于G/D=0.1时的压力差,因此对CLRMS有较好的抑制效果。当G/D=1.0时,图 7上、下两侧的压力差明显增大,对照图 5也可以看出,此刻立管的CLRMS与单根立管的CLRMS十分接近。而当ω=0及π/4时,由于上、下两侧的压力差比较接近,因此对CLRMS仍有较好的抑制效果。当G/D=1.5时,ω=0,π/12及π/6带有附属杆的立管周围压力场与单根立管基本相同,因此对立管CLRMS抑制效果十分微弱,ω=π/4和π/3时的抑制效果也相对有所减弱,在研究范围内随着ω的增大,抑制效果变化不大。
|
| 图 8 ω=π/6时附属杆及立管周围压力场分布 Fig.8 The pressure distribution around the |
|
| 图 9 ω=π/4时附属杆及立管周围压力场分布 Fig.9 The pressure distribution around the |
|
| 图 10 ω=π/3时附属杆及立管周围压力场分布 Fig.10 The pressure distribution around the |
综上所述,由于附属杆的存在导致立管周围的压力场在不同的间隙比及来流角度下有较大差异。对照图 4和图 5可以看出,压力场的变化直接导致了立管拖曳力系数均值CDMean及升力系数均方根值CLRMS的变化。
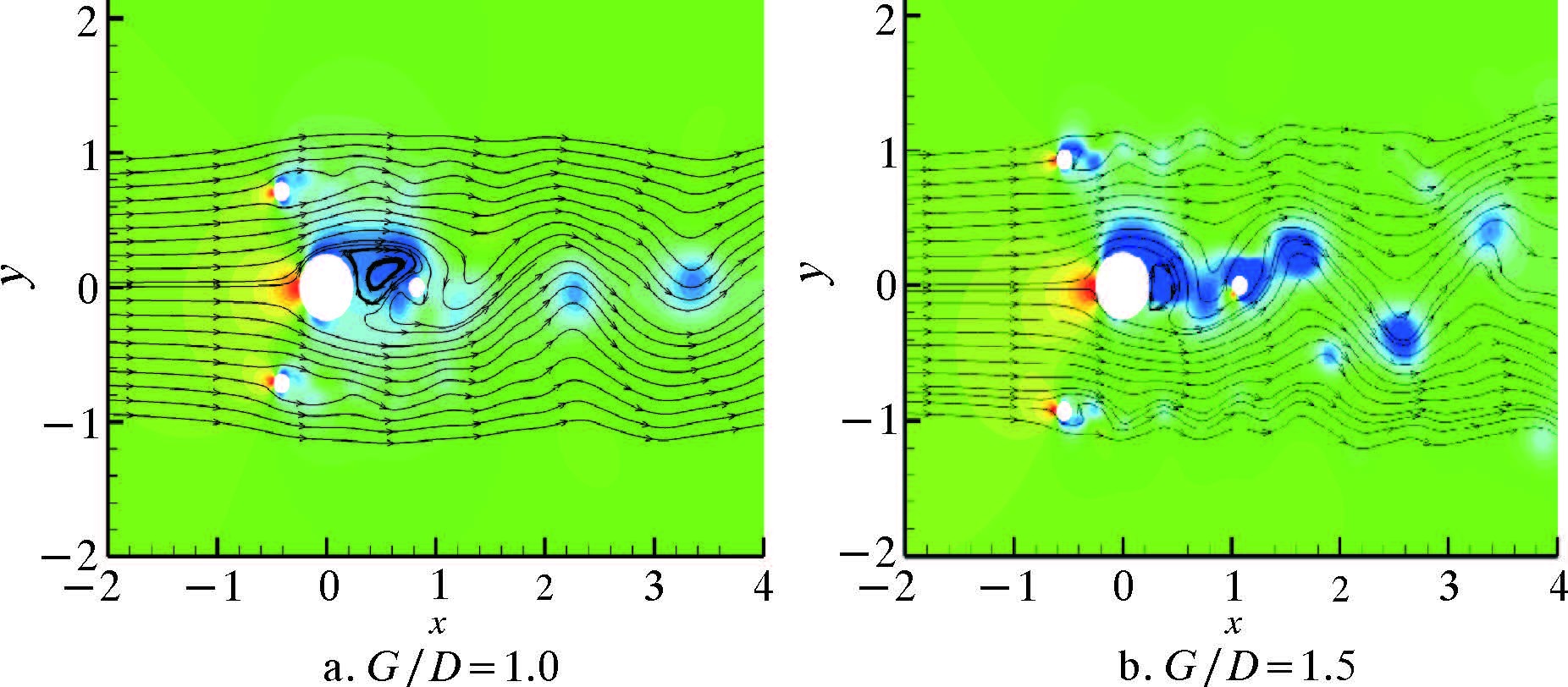
2.3 涡量场分析立管上的周期性泄涡是导致立管拖曳力及升力周期性变化的直接因素,附属杆的作用就是破坏立管周围的流场,进而破坏立管尾涡的周期性脱落,从而减小周期性泄涡对立管的破坏。本节研究附属杆对立管尾流涡街产生的影响。
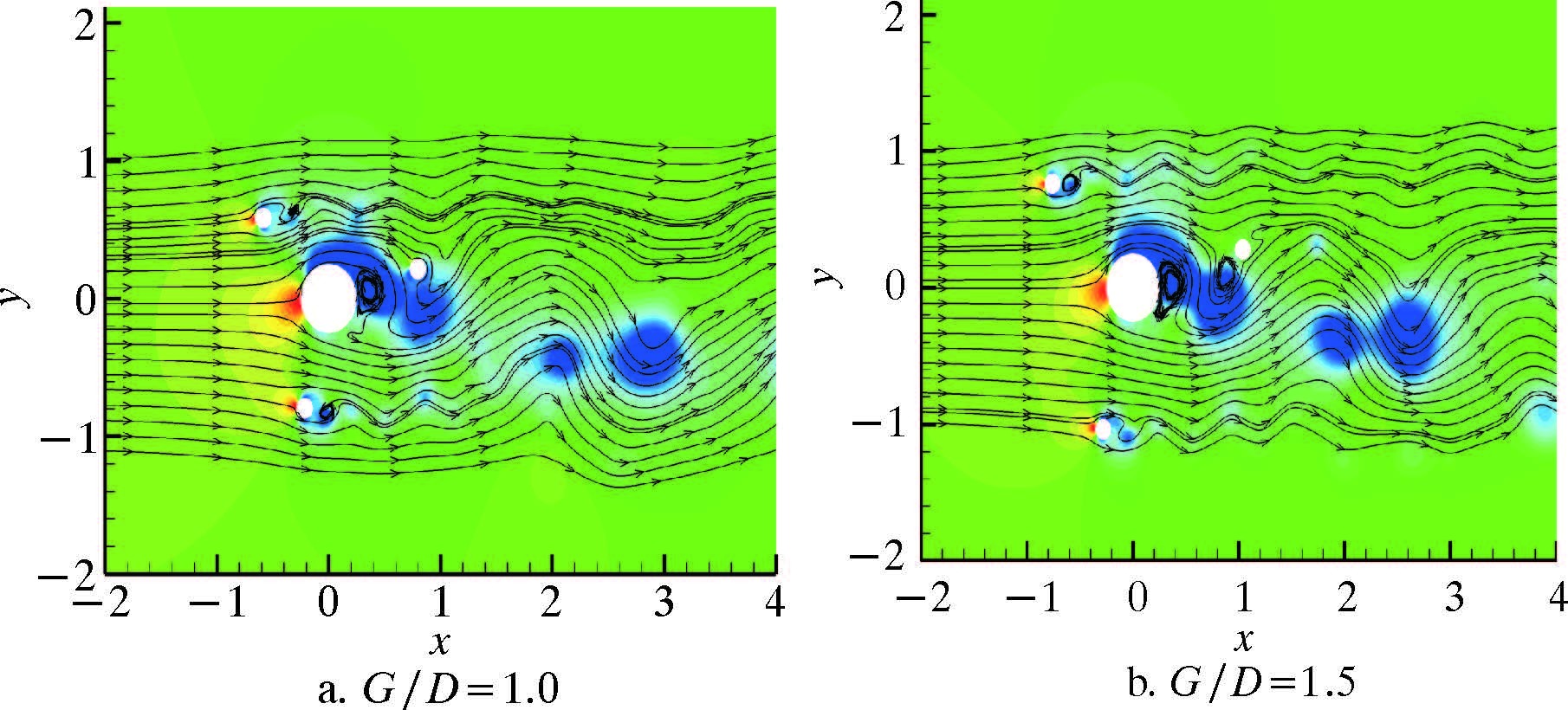
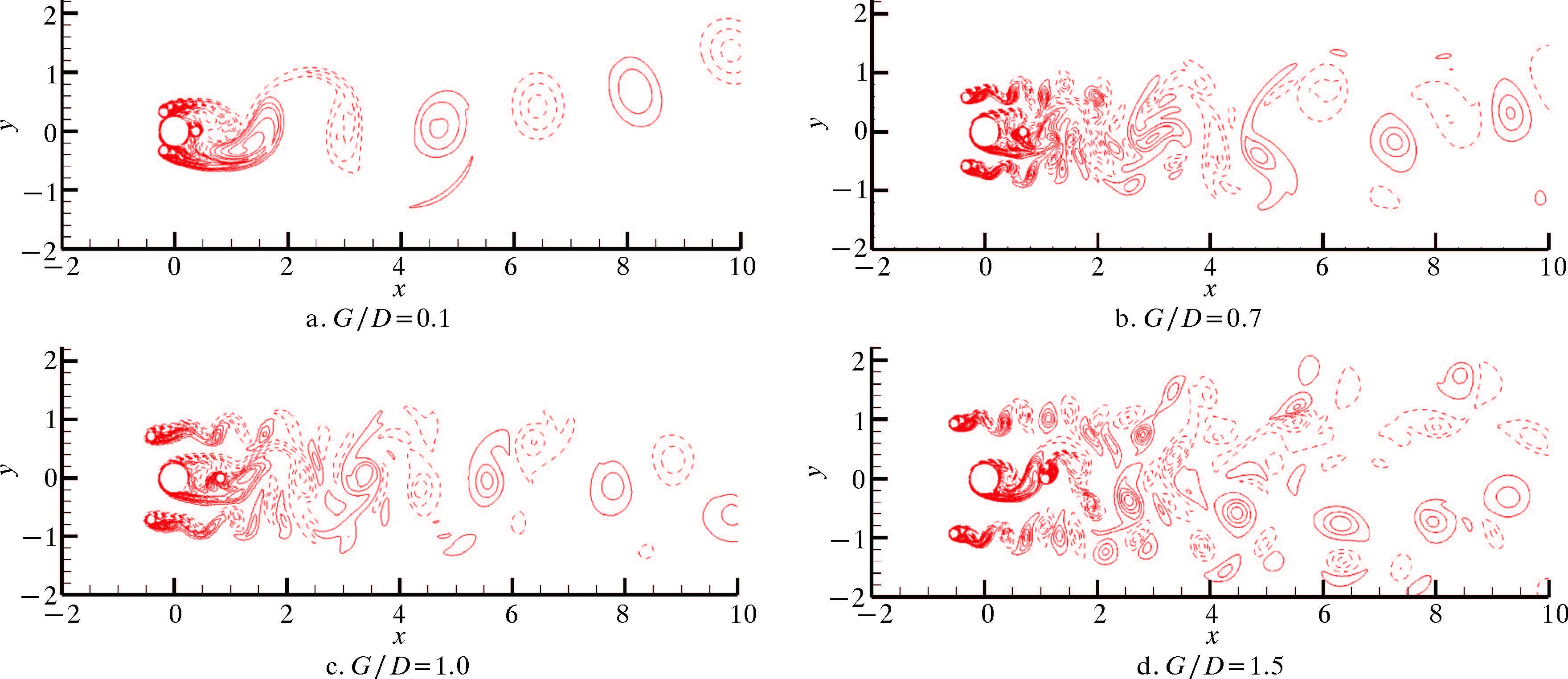
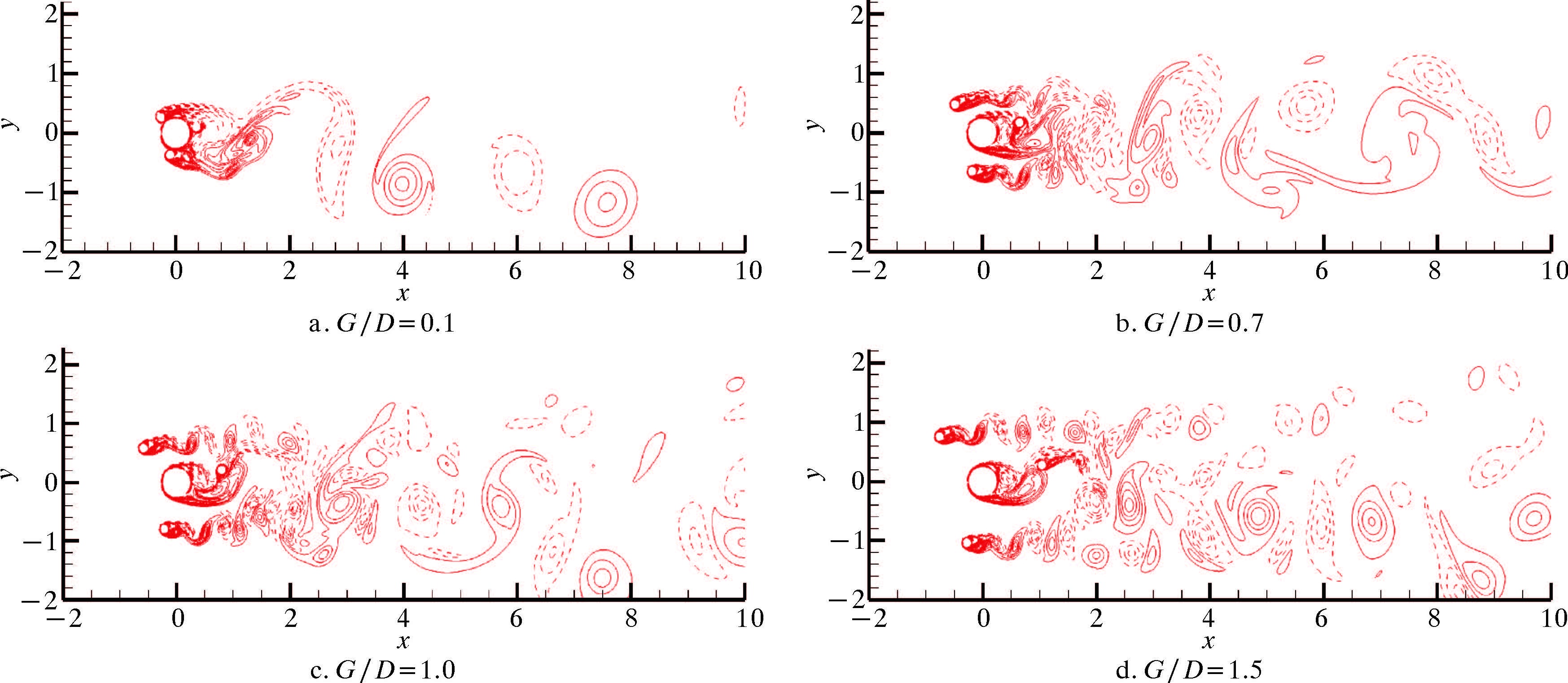
图 11~图 13是不同来流角度下,附属杆及立管周围涡量场分布。
|
| 图 11 ω=0时附属杆及立管周围涡量场分布 Fig.11 The vorticity distribution around the control rods and riser when ω=0 |
|
| 图 12 ω=π/12时附属杆及立管周围涡量场分布 Fig.12 The vorticity distribution around the control rods and riser when ω=π/12 |
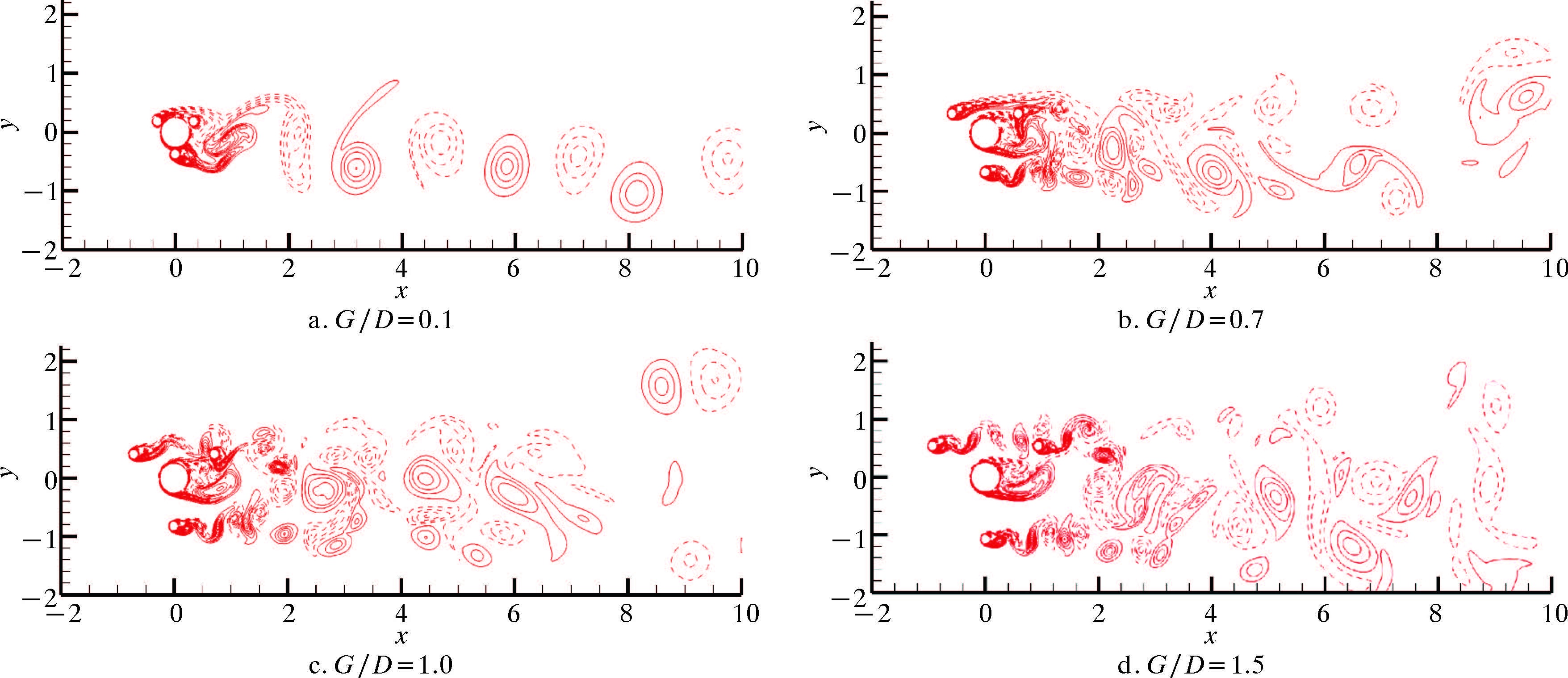
|
| 图 13 ω=π/6时附属杆及立管周围涡量场分布 Fig.13 The vorticity distribution around the control rods and riser when ω=π/6 |
从图 11~图 13可以看出,G/D=0.1时,各种角度下附属杆系统的涡量图与单根圆柱绕流涡量图几乎相同。这时由于附属杆与立管距离接近,附属杆的存在相当于增大了立管系统的有效直径,所以立管受到的CDMean大于单管。由图 11可以看出,当ω=0,G/D=0.7时,立管尾流处的涡街破坏程度较大,因此立管受到的CDMean和CLRMS均有较大程度的抑制,而随着G/D的增大,虽然有附属杆的存在,但是立管尾流中的涡街形式越来越明显,附属杆对立管泄涡的抑制效果逐渐减弱。如图 12所示,当ω=π/12、G/D=0.7时,立管后方没有规律的交替泄涡出现,而当G/D>1.0时,虽然后方有附属杆,但立管后方出现了明显的交替泄涡,从图 5也可以看到CLRMS在这2处变化很大。如图 13所示,ω=π/6与ω=π/12比较相似,只是泄涡的抑制区间更大。若ω=π/4和ω=π/3,且当G/D≥1.0时,后方的附属杆对立管的影响很小,此时的抑制机理与G/D<1.0时有所不同,主要原因是:前方的附属杆泄涡频率与立管的泄涡频率不同,从而破坏了立管的周期性泄涡,导致了CLRMS的下降。虽然立管后方存在泄涡,但涡量的大小和强度都比单根立管小。因此,附属杆的存在对立管系统的泄涡具有一定的抑制作用,导致CDMean和CLRMS的降低。
3 结 论(1) 附属杆对立管涡街及其产生的拖曳力系数平均值和升力系数均方根值有较好的抑制效果,对立管的泄涡有较好的抑制效果。当G/D=0.7~0.8时,对于不同的来流角度均有较好的抑制效果,此时对CLRMS的抑制率可以超过75%。
(2) 间隙比G/D和来流角度ω对附属杆的抑制效果影响较大,G/D过小或过大都不能达到较好的抑制效果。从G/D>1.0开始,立管受到的拖曳力均方根值CLRMS对来流角度比较敏感,不同来流角度的CLRMS相差较大。
(3) 若来流角度ω=π/3和π/4,且在不同间隙比下的抑制机理有所不同,G/D=0.4~0.8时,主要是立管后方的附属管破坏立管尾流中的泄涡从而达到抑制效果;而当G/D≥1.0后,主要是立管前方的附属杆的泄涡频率与立管不同,导致立管CLRMS的降低。
| [1] | LEE L,ALLEN D W,HENNING D L,et al.Damping characteristics of fairings for suppressing vortex-induced vibrations[C]//23rd International Conference on Offshore Mechanics and Arctic Engineering.2004:433-438. |
| [2] | ASSI G R S, BEARMAN P W, KITNEY N. Low drag solutions for suppressing vortex-induced vibration of circular cylinders[J]. Journal of Fluids and Structures, 2009, 25 (4) :666–675 . |
| [3] | ZHAO M, CHENG L, TENG B, et al. Numerical simulation of viscous flow past two circular cylinders of different diameters[J]. Applied Ocean Research, 2005, 27 (1) :39–55 . |
| [4] | SARVGHAD-MOGHADDAM H, NODVID N. Numeric- al simulation of flow over two side-by-side circular cylinders[J]. Journal of Hydrodynamics, 2011, 23 (6) :792–805 . |
| [5] | 鞠少栋, 陈国明, 盛磊祥, 等. 基于CFD的深水隔水管螺旋列板几何参数优选[J]. 中国石油大学学报(自然科学版), 2010, 34 (2) : 110–113 . |
| [6] | 沙勇, 曹静, 张恩勇, 等. 抑制涡激振动的螺旋列板设计参数研究[J]. 海洋工程, 2013, 31 (1) : 43–48 . |
| [7] | 魏泽, 吴乘胜, 倪阳. 基于正交设计和CFD模拟的Spar平台螺旋侧板水动力优化设计研究[J]. 船舶力学, 2013, 17 (10) : 1134–1139 . |
| [8] | 徐枫, 陈文礼, 肖仪清, 等. 行波壁抑制圆柱涡激振动的数值模拟研究[J]. 工程力学, 2014, 31 (9) : 104–111 . |



