2. 哈尔滨工程大学机电学院
2. College of Mechanical and Electrical Engineering, Harbin Engineering University
0 引 言
在水下生产系统发生泄漏的情况下,采用应急救援转接的控油装置可减少水下油气泄漏污染,从而为我国海洋石油开发提供重要的应急保障。
控油装置在海底转接作业过程中,横向方向受到内部泄漏载荷和海流力,竖向方向受到水压力和自重载荷,为了保证控油装置不发生失稳现象,需确定合理的控油装置入泥深度。笔者以我国南海300 m水深和黏性海土为作业背景,建立了控油装置稳定性计算模型,对地基承载力、抗滑移和抗倾覆进行研究,以期为水下设施泄漏救援转接作业提供一定的理论基础。
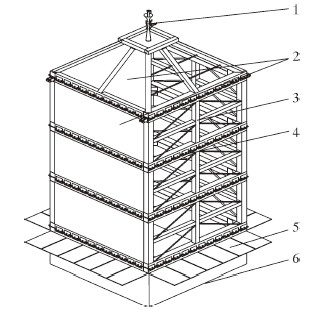
1 控油装置结构及力学模型 1.1 三维结构控油装置结构是由板结构和框架结构组成的板架体系。其主要由支撑框架、防沉板和下沉钢板基础组成。钢板的作用是使控油装置形成密闭集油空间,框架结构保证控油装置的整体强度和刚度。为了保证控油装置在深水作业所需的强度,采取减小梁柱的布置间距、人字斜撑支撑形式以及对称式结构等设计等方法。考虑到运输问题,控油装置选择分层组装,层与层之间选用丁腈橡胶垫片密封,通过外接螺栓连接,使得控油装置更易于安装。控油装置三维结构如图 1所示。
|
| 图 1 控油装置三维结构 Fig. 1 Three-dimensional structure of the oil control device |
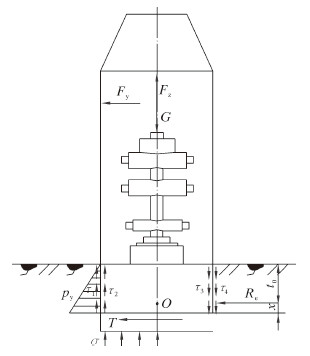
控油装置依靠自身重力克服黏性海土阻力后,下沉至防沉板底部,建立控油装置入泥后的稳定性分析模型(见图 2),由极限平衡条件求得控油装置的转动点以及满足控油装置在海底载荷下稳定的入泥深度[1]。假定控油装置防沉板与下沉钢板底部距离,即入泥深度为d,在距离海床高度h1和h2处,分别有内部泄漏载荷Fc及海流力Fl的作用,其中Fc大小由流体力学仿真分析得出,控油装置将会绕着海床下某一点O发生转动。此时,水平方向上除了Fc和Fl之外,还包括了控油装置左侧土体的水平抗力Fp,右侧土体的水平抗力Fa,海土作用于钢板底部的水平切力R,钢板底部的土反力σ,钢板内外海土对板壁的竖向作用力τ1、τ2、τ3、τ4,以及控油装置自重G和其他竖向作用力Fs[2],其中横向力大小为Fy=Fc+Fl,力臂可由等效力矩求得,受力如图 2所示。
|
| 图 2 控油装置稳定性分析模型 Fig. 2 Stability analysis model for the oil control device |
由于插入式钢板基础结构尺寸较大,而入土深度较小,一般认为在极限状态时,结构的转动点位于下沉钢板之下,在外载荷作用下,控油装置将绕O点向左发生转动。在极限状态设计方法中,可将控油装置钢板左、右两侧水平土抗力py和Rc,海土对钢板底部的摩阻力T,基底反力σ,左侧钢板内、外土体对钢板向上的竖向摩擦力τ1和τ2视为达到了极限值,若右侧钢板所受竖向力τ3和τ4也达到极限状态时的摩擦力的话,易导致不满足竖向力平衡条件,因此,右侧钢板所受摩擦力需要乘以折减系数λ[3]。
由控油装置所受水平力平衡条件可得:
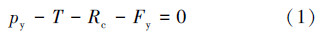
由控油装置所受竖向力平衡条件可得:
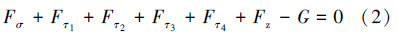
由对转动点O的力矩平衡条件得:
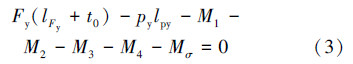
由式(1)、式(2)和式(3)联立求解可以得出3个未知量,即折减系数λ、距离t0和x,从而可计算出控油装置转动点的位置,得到满足稳定性要求的入泥深度d=t0+x。
2 控油装置稳定性分析 2.1 最小入泥深度的确定基础埋置深度是指控油装置下沉钢板底面与海床的距离,即为入泥深度。控油装置在海底环境进行转接救援工作时,若控油装置水平方向所受内部泄漏压力和底流力的载荷超过控油装置能承受的极限力矩,即发生失稳[4]。
2.1.1 海流力计算海流力是作用在控油装置上的一种流动阻力,相比海面波浪流,海流和潮流的速度变化缓慢,因此海流可看作是稳定流。根据各地学者的测量,海流速度一般在3~250 cm/s之间[5],作用在控油装置上的流水压力标准值可按照式(4)计算确定:
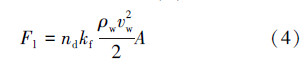
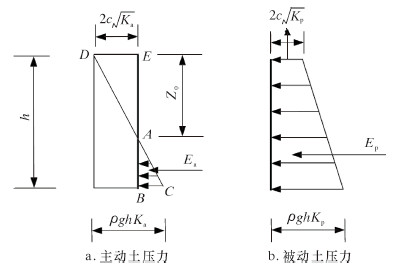
控油装置下沉钢板在黏性海土中,其左侧所受被动土压力包括因海土的自重引起的土压力和黏聚力引起的负压力,叠加后其压力沿下沉钢板呈梯形分布,作用点位于梯形面积重心上[6],如图 3b所示。右侧受到叠加的主动土压力结果如图 3a所示。
|
| 图 3 黏土侧壁土压力 Fig. 3 Sidewall pressure of the clay soil |
朗肯土压力理论根据土体所处的极限平衡状态时的最大主应力与最小主应力[7],根据控油装置下沉钢板尺寸大小,得到黏性海土中,其钢板所受主动土压力和被动土压力计算公式如下:
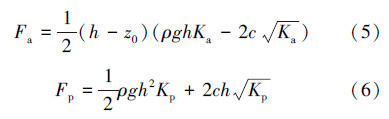
当海床土质为黏土时,采用API方法求取控油装置侧壁的摩擦力。控油装置单位面积侧壁摩擦力计算模型为:

因此,钢板单位宽度板壁的竖向摩擦力为:
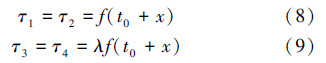
黏性土壤中f=5,由钢板结构可得Fτ1=Fτ2=Fτ3=Fτ4=fA=35λ(t0+x),lτ1=lτ2=lτ3=lτ4=3.5 m。式中:α为黏着系数;Su为黏土的不排水抗剪强度,kPa;Su<24.5 kPa,α=1.0;24.5 kPa<Su<73.0 kPa,α的大小随着Su呈直线下降趋势;如果Su>73.0 kPa,α=0.5。α值一般由经验取得,因此侧壁摩擦力一般小于200 kPa[8]。
2.1.4 土切力及基底反力计算控油装置受到海底水流力和泄漏压力的水平载荷作用,控油装置底部海土会对下沉钢板基础产生切力,可采用下式计算:
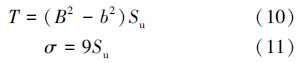
控油装置在黏土中的底部摩阻力为T=4.2 kN,lT=x。求得黏土中,σ=45 kPa,因此Fσ=σA=75.1 kN,lFσ=1.75 m。
将控油装置土作用力及力矩代入极限平衡方程式(1)、式(2)和式(3),求解控油装置在黏土中满足稳定的最小入泥深度为2.24 m,因此,设计控油装置下沉钢板深度为3 m。
2.2 稳定性分析控油装置吊装下放水下设施泄漏处,下沉钢板插入海床土层中,控油装置稳定性分析,包括竖承载力稳定、抗滑移稳定和抗倾覆稳定[9]。其中承载力稳定是控油装置抗滑移和抗倾覆的前提条件。本节选取控油装置最危险的工况进行计算,即内部泄漏方向和外部海流方向均为0°,来进行抗倾覆和抗滑的稳定性校核。满足控油装置稳定的入泥深度由2.1节计算得到为3 m。下面对控油装置进行稳定性分析。
2.2.1 地基稳定分析关于控油装置竖向极限承载力的计算,依据海洋工程经验公式,将控油装置下沉钢板与海土的侧壁摩阻力与底部桩端阻力之和视为控油装置竖向极限承载力,即Qu=Ff+Fσ,其中侧壁摩阻力和底部桩端阻力按照式(7)和式(11)计算,从而得到黏土中的竖向极限承载力[10],表达式为:
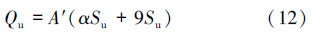
控油装置保持竖向稳定,应分为2个方向考虑。即在竖直下方向,Fz不能超过下沉钢板的竖向极限承载力,即Fz+G<8Ff+Qu;在竖直上方向,Fz应满足不能使控油装置发生漂浮,即Fz<G+8Ff。由式(12)计算出Qu=1 662 kN,由此可得到Fz保持稳定的范围是-882 kN<Fz<2 220 kN。Fz的大小由内、外压差所决定,因此可以通过调节顶端转接出口压力来调节内部压力场所引起竖向力Fz,使得控油装置保持稳定。
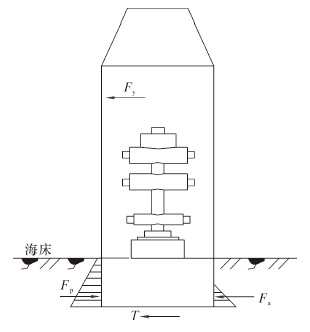
2.2.2 抗滑移分析选择控油装置下沉钢板插入海床的接触面为滑移面,底部滑动力为控油装置受到的水平力之和,由内部横向压力和底流流力组成。主被动土压力和土体对钢板底部的水平切力如图 4所示。控油装置在正常作业时,抗滑移安全系数应不小于1.4。
|
| 图 4 抗滑受力图 Fig. 4 Schematic of anti-sliding forces |
由图 4中关系可知,控油装置结构底部抗滑移稳定性按如下方法验算:

通过式(5)和式(6),由控油装置尺寸参数,可以计算得在黏土中,保持不发生滑移的极限横向力Fh=1 618.2 kN。可简化计算求得横向力Fy,在压力为4、10和16 MPa的采油树管口侧向发生泄漏的情况下,控油装置保持稳定的泄漏管口大小与海底流速度之间的关系。经计算可以得到在横向力Fy中,泄漏口的横向作用力是主要原因,海流速度是导致滑移的次要因素。若不考虑因泄漏引起发生因素时,当控油装置外部海流流速达到3.17 m/s时,控油装置发生滑移失稳,其关系整理如图 5所示。

|
| 图 5 泄漏管口直径与底流流速关系 Fig. 5 The relation of leakage pipe diameter and the bottom flow velocity |
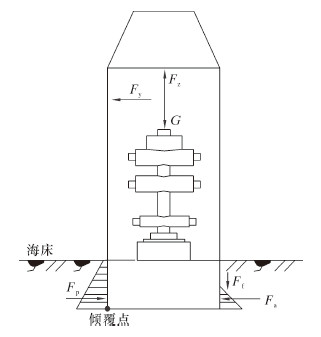
在内部泄漏油压作用下,控油装置结构的抗倾覆稳定性应具有一定的安全保证。根据《防波堤设计与施工规范》,对于插入式箱型基础,在抗倾覆稳定性计算中,选取钢板基础前趾点为抗倾覆力矩和倾覆力矩的中心点来进行抗倾覆力学分析,抗倾受力如图 6所示。控油装置在海底救援转接时,产生倾覆力矩的有横向力Fy、自重G和主动土压力Fa,产生抗倾覆力矩的有竖向力Fz、被动土压力Fp、钢板壁面摩擦力Ff和土体的黏聚力和吸附力,在计算中,可以忽略作用较小的有利因素。
|
| 图 6 抗倾受力图 Fig. 6 Schematic of anti-overturning forces |
由图 6中关系可知,控油装置结构前趾点抗倾覆稳定性按如下方法验算:

控油装置倾覆力矩为:
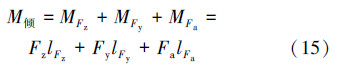
控油装置抗倾覆力矩为:
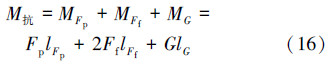
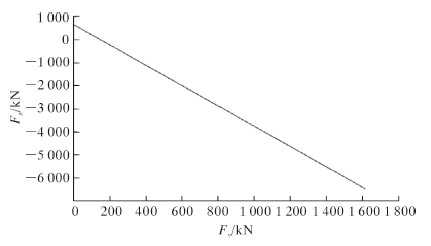
联立式(15)和式(16)可以得出关系式3.5Fz+14.5Fy-2 322 600=0,根据控油装置滑移和倾覆条件,在保证控油装置发生不发生滑移破坏的条件下,即0<Fy<1 618.2 kN时,可以得到Fz与Fy的关系,如图 7所示。
|
| 图 7 横向力与竖向力关系 Fig. 7 The relation of lateral force and vertical force |
由图 7可以看出,在保持控油装置不发生滑移破坏的前提下,随着横向力Fy增大至150.4 kN时,控油装置不发生倾覆的竖向力方向发生改变,即控油装置整体受到Fz<0,才能使其保持稳定,不发生倾覆。当横向力Fy增大至达到发生滑移的极限时,即Fy=1 618.2 kN时,需要方向向下的竖向力Fz=6 475.8 kN,才使得控油装置不发生倾覆失稳。
通过流体力学仿真分析和海流力计算可知,Fy=306.6 kN,计算出控油装置保持稳定所需要向下的竖向力Fz=662.3 kN。
按照设计要求,取海底水流速度为0.25 m/s,泄漏设施的漏口压力值为4 MPa,泄漏面积为0.11 m2,控油装置入泥深度3 m,计算控油装置所受各力值整理如表 1所示。
| 载荷名称 | 作用力/ kN | 力臂/ m | 力矩/ (kN·m) |
| 海底流力Fl | 21.60 | 14.50 | 313.20 |
| 主动土压力Fa | 235.20 | 0.40 | 94.10 |
| 被动土压力Fp | 1 028.40 | 0.97 | 997.20 |
| 侧壁摩擦力Ff | 90.00 | 7.00 | 630.00 |
| 竖直向下力Fz | 662.30 | 3.50 | 2 318.00 |
| 控油装置自重G | 1 176.00 | 3.50 | 4 116.00 |
| 横向力Fy | 285.00 | 18.20 | 5 214.20 |
(1)以我国南海300 m水深和黏性海土为作业背景,建立了水下井口控油装置的力学分析模型,确定了该条件下控油装置保持稳定的最小入泥深度为3 m。
(2)对控油装置在黏性海土下的土作用力进行计算,得到了控油装置保证地基、抗滑移和抗倾覆稳定与其所受横向力和竖向力之间的关系,得到控油装置可抗海流速度极限为3.17 m/s。
(3)经计算求得,控油装置在黏土中其结构底部抗滑移安全系数为2.78,故控油装置在保持地基稳定的前提下,当入泥深度h=3 m时前趾点抗倾覆和抗滑移均满足设计预期稳定性要求。
(4)通过对控油装置稳定性进行分析研究,可为实际工程作业提供理论支持。
| [1] | 黄志全,周进.单桩桩土作用及其理论计算方法研究[J].山西建筑,2008,34(1):3-4. |
| [2] | 封晓伟.波浪循环荷载作用下防波堤-地基稳定性研究[D].天津:天津大学,2010. |
| [3] | 王元战,董少伟,王玉红.沉入式大圆筒结构入土深度计算方法研究[J].水利学报,2004(4):96-100. |
| [4] | 张雯雯.插入式箱型进海路结构研究[D].天津:天津大学,2012. |
| [5] | 王泽中.海洋学研究的新知——深海底流沉积[J].大自然探索,1997,16(3):86-89. |
| [6] | 李镜培,赵春风.土力学[M].北京:高等教育出版社,2004:159-167. |
| [7] | 王元战,郭富林,刘旭菲,等.格型钢板桩结构抗倾覆稳定性与地基承载力的计算方法[J].港工技术,2013,50(2):32-35. |
| [8] | BRANDON T L,ROSE A T,DUNCAN J M.Drained and undrained strength interpretation for low-plasticity silts[J].American Society of Civil Engineers,2006,132(2):250-257. |
| [9] | 何德磊.崖城13-4气田水下井口强度和稳定性分析研究[D].北京:中国石油大学,2011:9-13. |
| [10] | 张连丽.软土地基上新型港工结构承载特性与稳定性分析方法研究[D].天津:天津大学,2013:21-23. |



