0 引 言
随着钻井技术的发展,井下牵引器在测井和修井等井下作业领域得到了广泛应用。受工况条件限制,井下牵引器的胀闸、伸缩和扶正等主要结构以串联方式连接,其径向尺寸远小于轴向尺寸[1, 2],在运动和工作过程中,易发生弯曲变形。因此采用弹性元件作为扶正机构的扶正臂,依靠其弹性变形实现扶正作用,同时对机器人的运动进行定位和支撑[3, 4, 5]。
井下牵引器扶正机构扶正臂的弹性系数与其结构参数密切相关,在设计时需进行优化。一般地,解决此类柔性机构的结构参数设计、受力与变形等问题通常采用椭圆积分和非线性有限元法[6, 7]。陈智等[8]采用平面曲杆受力与变形模型结合ANSYS有限元分析软件对弓形弹簧进行了分析。艾池等[9]利用卡氏定理和莫尔定理对弹性限位扶正器的扶正力和位移做了分析,计算结果在小变形条件下比较理想,没有分析弹性杆件的大变形情况。这些方法侧重于选定设计时的参数验算,不适用于优化设计阶段。笔者采用“伪刚体模型”法[10]进行研究,利用刚性构件的位移和转角来近似替代柔性部件的变形,避免了对非线性弹簧函数进行复杂的微积分运算,结合虚功原理,分析扶正臂受力、变形及结构参数之间的关系,对其结构参数进行优化设计。笔者的研究为分析、设计非线性大变形弹性机构提供了一种简单的解决方法。
1 扶正臂构型分析图 1所示为井下牵引器结构简图。牵引器由2个胀闸机构、2个扶正机构和1个关节机构串联组成,每个扶正机构具有4条沿圆周方向对称布置的扶正臂,支撑牵引器使其位于油管轴线附近。

|
| 图 1 井下牵引器结构简图 Fig.1 Structural schematic of downhole tractor 1、8-胀闸机构;2、6-扶正机构; 3-扶正臂;4-关节机构;5-铰支座;7-销轴。 |
井下牵引器进入管道以后,扶正臂受到管道内壁压迫产生弹性变形。取1条扶正臂作为分析对象,设A、B为扶正臂两端铰接点,A端固定铰支,B端为活动铰支可在AB连线方向运动。以A点为原点,AB——为x轴,建立直角坐标系,受力变形情况见图 2。图中:D为油管内壁直径,mm;d为扶正臂铰支座直径,mm:w、h为扶正臂横截面的宽度及高度,mm;R0、R为扶正臂初始及受力变形后的半径,mm;a0为端面初始距离,mm;a为变形后端点距离,mm;b0、b分别为扶正臂初始与受力变形后弧的高度,mm;θ0、θ分别为扶正臂端部初始和受力后的变形角,rad;l为扶正臂长度,mm。
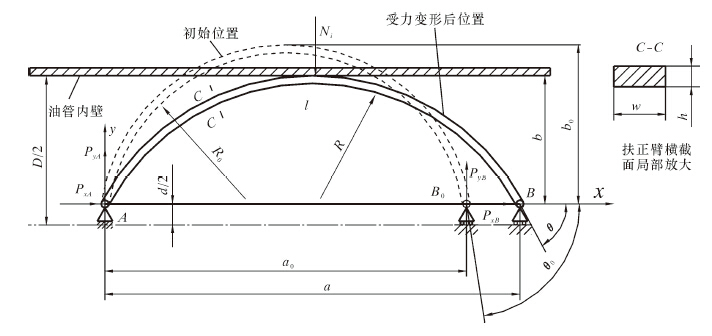
|
| 图 2 扶正臂受力变形简图 Fig.2 The forces and deformation of the centralizer arm |
若扶正臂在其与油管内壁接触处受到径向压力为Ni,A点支反力为PxA、PyA,B点支反力为PxB、PyB,则有PxA=PxB=0,PyA=PyB=Ni/2。
用伪刚体模型法对扶正臂受力变形进行构型,如图 3所示。图中:Θ0、Θ分别为AC杆与水平方向上的初始与运动后的夹角,rad;K为特征铰链的弹簧常数,N/m;γ为特征半径系数,无量纲;ρl/2为伪刚体杆长度,mm。
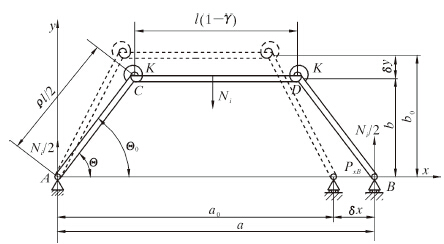
|
| 图 3 扶正臂的伪刚体构型示意图 Fig.3 Schematic pseudo-rigid-body configuration of centralizer arm |
用AC、BD和CD 3段伪刚体杆来模拟扶正臂,AC、BD 2段长度均为ρl/2且关于扶正力Ni作用线对称。 C、D点处加入刚度系数为k的特征铰链来模拟扶正臂在弯曲时所产生的反力,其力矩T=k(Θ-Θ0)。
2 扶正臂伪刚体构型的扶正力方程 2.1 扶正臂变形与扶正力关系根据虚功原理,扶正臂处于平衡状态时,总虚功为0,则有:







如图 2所示,根据Bernoulli-Euler方程1/R0=dθ/ds,有2R0θ0=l,求得扶正臂B端在水平和垂直方向上的初始位置表达式为:

根据文献[10],特征铰链刚度系数kΘ、特征半径系数γ和弹簧常数K的表达式分别为:



由图 3所示几何关系可得:

设扶正臂横截面为宽w、高h的矩形,整理得单条扶正臂伪刚体构型的扶正力方程:
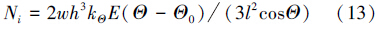
此时,扶正臂半段可视为悬臂梁,其最大应力发生在扶正臂的中间位置,其数值为:

由于管道存在局部缩颈、错位和扩径,设计时考虑管径扩大率在λ=±10%范围内的情况。设管径扩大率为10%时,扶正臂处于初始状态,扶正力Ni为0;管径扩大率为0时,扶正臂处于正常工作状态。在进行l、R、w和h等扶正臂结构参数优化时,应保证在满足正常工作所需扶正力的条件下体积最小。
设油管内壁直径D和扶正臂铰支座直径d为常量,扶正臂横截面宽度w根据结构需要预先选定。ρl、γ、cosΘ作为中间变量由l、R表示,在Ni一定时,通过选择不同的l、R、h组合,可以得出最优的Vmin值。为此,设计变量可以表示为:

由式(13),得目标函数表达式为:



根据井下牵引器结构设计要求,扶正机构轴向长度L∈[200,600],单位为mm。因此,扶正臂变形后两端铰接点的轴向距离a应满足条件:a(200,600),即有:
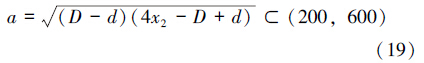
扶正臂的曲率大于0且弧长大于管道内径,其2倍弦高与铰支座直径之和应当大于管道内径,于是有:

根据式(10)成立的前提条件,可得:

扶正臂材料选定以后,最大厚度Hmax根据弹簧钢材在油中能淬透的最大厚度确定。设扶正臂材料为60Si2MnA,则材料在油中能够淬透的最大厚度[11]Hmax=25 mm。
低速运动的牵引器可视为承受静载荷,扶正臂许用应力[11]取抗拉强度[σ]b的75%,则有:

当井眼扩大率λ=-10%时,扶正臂最大应力σ2max的值为:

根据式(14)、式(22)和(23),得强度条件为:
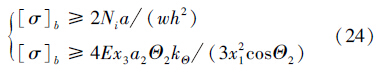



已知管道内径D=150 mm。井下牵引器具有2组扶正机构,每个扶正机构具有4条沿圆周方向对称布置的扶正臂,扶正臂材料选用60Si2MnA,弹性模量E=198.00 GPa,抗拉强度[σ]b=1 372 MPa,剪切模量G=79.84 GPa,泊松比μ=0.29,铰支座直径d=70 mm。管径扩大率为0时,1条扶正臂产生的扶正力Ni=200 N,扶正臂横截面宽度w=10 mm。
经计算,得扶正臂长度l、曲率半径R、横截面高度h及最大应力值σmax,如表 1所示。
| 数据分组 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| l/m | 0.32 | 0.44 | 0.53 | 0.53 | 0.61 | 0.61 | 0.61 | 0.61 | 0.62 | 0.62 | 0.62 | 0.62 | 0.62 | 0.62 | 0.62 |
| R/m | 0.26 | 0.50 | 0.73 | 0.73 | 0.97 | 0.97 | 0.97 | 0.97 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| h/mm | 3.00 | 4.00 | 5.00 | 6.00 | 5.00 | 6.00 | 7.00 | 8.00 | 5.00 | 6.00 | 7.00 | 8.00 | 9.00 | 10.00 | 11.00 |
| a/mm | 275 | 389 | 473 | 473 | 547 | 547 | 547 | 547 | 556 | 556 | 556 | 556 | 556 | 556 | 556 |
| σ1max/MPa | 1 060 | 831 | 642 | 446 | 739 | 513 | 377 | 289 | 751 | 522 | 383 | 294 | 232 | 188 | 155 |
| σ2max/MPa | 1 360 | 906 | 766 | 919 | 572 | 686 | 801 | 915 | 553 | 664 | 774 | 885 | 995 | 1 110 | 1 220 |
| Δσ/MPa | 300 | 75 | 124 | 473 | -167 | 173 | 424 | 626 | -198 | 142 | 391 | 591 | 763 | 922 | 1 065 |
由表 1可知,扶正臂长度l及曲率半径R确定时,随着横截面高度h的增加,管径扩大率为0时的扶正臂最大应力σ1max呈下降趋势,而井眼扩大率λ=-10%时的扶正臂最大应力σ2max不断增加,当h≥10 mm时,σ2max=1 110 MPa,超过扶正臂材料抗拉强度的75%。扶正臂最大应力值的变化幅度Δσ随之增加,若扶正臂长期工作在较大应力变化的条件下,易产生疲劳失效。
当扶正臂轴向长度a≤275 mm时,扶正臂最大应力σ2max=1 360 MPa,超过扶正臂材料抗拉强度的75%。
综合考虑扶正臂结构尺寸和应力情况,优选表 1中第2组数据作为扶正臂设计的结构参数,此时应力值变化幅度Δσ最小,同时满足尺寸最小的优化条件。
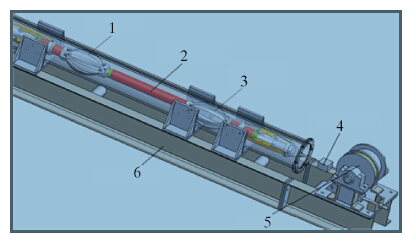
4.2 水平管道爬行扶正力测量试验扶正机构试验台如图 4所示。井下牵引器安装2个扶正机构,每个扶正机构有4条扶正臂,扶正臂的结构尺寸由前述优化计算确定。将牵引器置于地面水平管道内爬行,用拉力传感器测量牵引器通过管道时扶正机构与管道内壁之间的摩擦力。
|
| 图 4 扶正机构试验台 Fig.4 Centralizer mechanism test device 1、3-扶正机构;2-井下牵引器;4-拉力传感器;5-绞车;6-试验台底座。 |
利用绞车拉动井下牵引器,旋转绞车调节螺母调节刹带与绞车间的摩擦力,记录拉力传感器显示的数据。测得扶正机构与管道内壁之间的摩擦力F=300 N,见表 2。
| 刹带螺母旋进圈数 | 拉力传感器示数/N | 是否打滑 |
| 5 | 80 | 是 |
| 10 | 140 | 是 |
| 13 | 230 | 是 |
| 14 | 260 | 是 |
| 15 | 300 | 否 |
设1条扶正臂产生的扶正力为N,扶正臂与管道内壁之间的摩擦因数μ=0.15,则牵引器扶正机构与管道内壁产生的摩擦力之和F=8Nμ=1.2(N)。根据表 2中的试验数据,得最大摩擦力时扶正臂产生的扶正力N=F/1.2=245(N)。与优化设计时的预设条件扶正力Ni=200 N相比,较为接近。存在误差的原因在于管道内壁较为粗糙,与扶正臂之间的摩擦因数要大于0.15。
5 结 论(1)建立了井下牵引器扶正机构扶正臂的伪刚体模型并进行优化求解,得到在扶正臂长度及曲率半径不变的情况下,随着横截面高度的增加,扶正臂工作在正常管径和缩颈区域最大应力值的变化幅度随之增加的结论,优选出适用于150 mm管径的井下牵引器扶正机构扶正臂的结构参数。
(2)推导出扶正臂的优化设计模型及求解方法,在确定扶正臂受力与变形之间的关系时,避免了对非线性弹簧函数进行复杂的微积分运算,建模和计算比较简单,适合在精度要求不高的条件下使用。研究内容为分析和设计非线性大变形机构提供了一种简单的解决方法。
(3)试验结果表明了模型的正确性,对类似的井下牵引器扶正机构及油田广泛使用的弓形弹簧套管扶正器的设计具有一定的参考价值。
| [1] | 西南石油大学.连续油管爬行器及其爬行方法:201110081197.2[P].2011-10-05. |
| [2] | 高胜,孙文,倪晗,等.石油井下牵引器设计现状及几点认识[J].机械设计,2014(2):1-8. |
| [3] | 侍红岩.非线性弓形弹簧的设计与仿真[J].山东工业技术,2014(9):7-8. |
| [4] | 舒中选,陈德东,郑严,等.常用套管扶正器扶正力及其变形关系的探讨[J].石油钻探技术,2003(5):82-84. |
| [5] | 张海山,张凯敏,宫吉泽,等.不同类型扶正器对水平井下套管摩阻的影响研究[J].钻采工艺,2014(3):22-25. |
| [6] | HETRIK J A,KOTA S.An energy formulation for parametric size and shape optimization of compliant mechanisms[J].Transaction of the ASME.Journal of Mechanisms in Design,1999,121(3):229-233. |
| [7] | HOWELL L L,MIDHA A.A loop-closure theory for the analysis and synthesis of compliant mechanisms[J].Transaction of the ASME.Journal of Mechanical Design,1996,118(1):121-125. |
| [8] | 陈智,丛强,胡强法,等.一种弓形弹簧的设计与应用[J].石油机械,2010,38(8):71-73. |
| [9] | 艾池,刘国勇,冯福平.弹性限位扶正器变形量对套管居中度的影响[J].西部探矿工程,2010(2):88-91. |
| [10] | HOWELL L L.柔顺机构学[M].余跃庆,译.北京:高等教育出版社,2007:310. |
| [11] | 徐灏.机械设计手册(第四卷)[M].北京:机械工业出版社,1992:15-30. |



