0 引 言
水平井工程是近些年发展起来的技术,钻柱是决定钻井能否成功的关键因素。在钻井过程中,钻柱承受着由交变载荷引起的较大应力突变,容易导致钻柱疲劳失效,造成巨大的经济损失[1, 2]。这就要求对钻柱的动力学特性进行研究,探明水平钻柱耦合振动动力学机理及钻柱耦合振动的控制方法。当前针对钻柱的研究主要集中在底部钻具组合部分(Bottom Hole Assembly,BHA),缺少对整体钻柱运动状态的研究[3, 4, 5, 6, 7]。范永涛[8]、管志川[9]等研制了水平井底部钻柱运动状态试验装置,研究了BHA段的运动特性。笔者基于相似理论和轴承-转子系统动力学理论研制了水平受压钻柱试验装置,通过对钻柱转速、轴向力、扭矩、钻井液、激振载荷等影响钻柱动力学行为的工艺参数的控制,实现对钻柱动力学关键行为参数的定量测量,通过室内试验的方式[10]探究水平受压钻柱的运动机理。
1 水平受压钻柱试验装置所遵循的相 似准则基于相似理论研制水平受压钻柱试验平台,首先要推导出相似准则,笔者选择方程分析法中的相似转换法推导相似准则,这种方法结构严密、分析过程明确,推导出的相似准则有明确的物理意义。
1.1 确定钻柱的基本微分方程根据轴承-转子系统动力学理论[11],取oxys坐标系,转轴轴线水平沿s方向,重力沿x方向,y方向垂直于oxs平面,可以得到质量均匀分布转子的微分方程为:
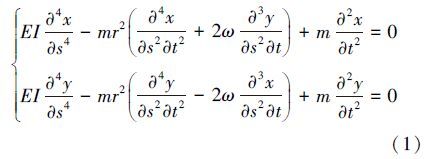
将水平受压钻柱简化成质量均匀分布、轴端受压的转轴,基于轴承-转子系统动力学,暂不考虑钻柱重力、偏心和内外阻尼的影响,考虑钻柱轴向压力的影响,则简化后的钻柱微分方程为:
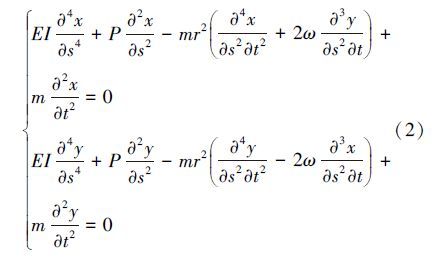
选取式(2)中第1式(每一式都可以)为原型的基本微分方程,式中分为4项,其中第1项$EI\frac{{{\partial }^{4}}x}{\partial {{s}^{4}}}$表示弯矩部分;第2项$P\frac{{{\partial }^{2}}x}{\partial {{s}^{2}}}$表示轴向力部分;第3项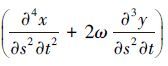 表示质量惯性矩部分;第4项$m\frac{{{\partial }^{2}}x}{\partial {{t}^{2}}}$表示惯性力部分。
表示质量惯性矩部分;第4项$m\frac{{{\partial }^{2}}x}{\partial {{t}^{2}}}$表示惯性力部分。
以式(2)中第1式为原型,将模型中的物理量以上标“′”表示,则模型的基本微分方程为:
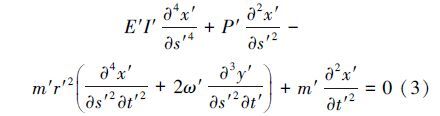
单值性条件是将现象群的通解转变为特解的具体条件,写出单值性条件并写出模型与原型物理量间的相似变换式(带上标“′”的为模型参数)。
密度比${{c}_{\rho }}=\frac{\rho '}{\rho }$,弹性模量比${{c}_{E}}=\frac{E'}{E}$,时间比${{c}_{t}}=\frac{t'}{t}$,质量比${{c}_{m}}=\frac{m'}{m}$,截面惯性矩比${{c}_{t}}=\frac{t'}{t}$,质量比${{c}_{I}}=\frac{I'}{I}$,转速比${{c}_{\omega }}=\frac{\omega '}{\omega }$,轴向力比${{c}_{P}}=\frac{P'}{P}$,井斜角比${{c}_{\alpha }}=\frac{\alpha '}{\alpha }$。
根据几何相似要求,单值性条件中的长度单位的物理量有相同的几何比cl,如钻柱外径D、内径d,钻柱长度l等。
利用相似变换式对基本微分方程进行相似转换。将相似变换式代入到基本微分方程式(3)中,将式(3)中所有带符号“′”的参量全部置换,整理后得到:
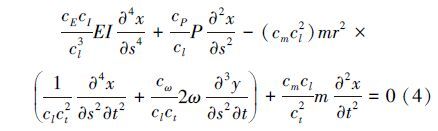
根据相似现象所具有的相似性质,使式(4)与原型微分方程(2)的对应相似常数相等,可以得到:
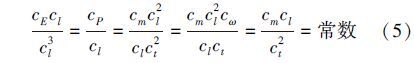
其中有质量表达式m=ρπ(D2-d2)/4,则模型质量表达式为m′=ρ′π(D′2-d′2)/4,通过相似转换式可以得到cm=cρcl2;钻杆为中空的圆柱体,截面惯性矩为$I=\frac{\pi \left( {{D}^{4}}-{{d}^{4}} \right)}{64}$,模型截面惯性矩表达式为$I'=\frac{\pi \left( D{{'}^{4}}-d{{'}^{4}} \right)}{64}$,通过相似转换式可以得到cI=cl4。
通过上述物理量中相互独立的相似变换式,可以导出其他不独立的相似变换式。由式(5)中$\frac{{{c}_{E}}{{c}_{I}}}{c_{l}^{3}}=\frac{{{c}_{P}}}{{{c}_{l}}}$可以得到${{c}_{P}}=\frac{{{c}_{E}}{{c}_{I}}}{c_{l}^{2}}$,因为cI=cl4,则可推出cP=cEcl2,整理得到相似指标方程$\frac{{{c}_{P}}}{{{c}_{E}}c_{l}^{2}}$=1。
由式(5)中$\frac{{{c}_{E}}{{c}_{I}}}{c_{l}^{3}}=\frac{{{c}_{m}}c_{l}^{2}}{{{c}_{l}}c_{l}^{2}}$可以得到cEcI=cmcl4cω2,因为cI=cl4,cm=cρcl2,则可推出cω=$\frac{1}{{{c}_{t}}}=\sqrt{\frac{{{c}_{E}}}{{{c}_{\rho }}c_{l}^{2}}}$,整理得到装置的相似指标方程$\frac{{{c}_{\rho }}c_{l}^{2}c_{\omega }^{2}}{{{c}_{E}}}$=1。
综上所述,水平受压钻柱试验装置与原型之间的相似准则为:
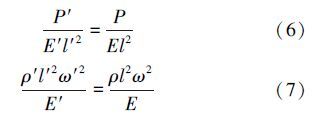
水平受压钻柱试验装置以水平井中钻柱为原型,在水平井钻采中,常用加重钻柱的外径127 mm,内径76 mm,单根长度8~12 m。选取单根钻柱长度10 m,钻柱总长度根据不同的水平井深来确定,该装置模拟总长度为50 m的钻柱,钻头外径311 mm。
2.1 模型与原型几何相似所有单值性条件中具有长度单位的物理量取相同的几何比,如钻柱的内外径和长度等,模型建立中几何比取cl≈1∶10。单值性条件中具有角度单位的物理量保持不变,如井斜角α,取cα=1[12]。
实际钻柱外径D=127 mm,内径d=76 mm,单根长度l=10 m,钻头外径Dz=311 mm。
模拟钻柱外径D′≈14 mm,内径d′≈8 mm,钻头外径D′z≈32 mm,钻柱单根长度l′=1 m,试验装置模拟钻柱总长度为5 m。试验装置通过内壁摩擦处理的井筒模拟井壁,井筒的内径由钻头外径确定,井筒内径d′t=D′z=32 mm。根据试验要求,为防止井筒磨漏,将井筒外壁加厚,因而选择井筒外径D′t=52 mm。
2.2 模型与原型物理学相似试验平台的主体-模拟钻柱的材料需要与真实钻柱的材料具有相同或者相近的应力-应变特性曲线,这样才能通过模拟试验呈现真实钻柱的运动状态。
钻柱的材料为高级合金钢,密度ρ=7.85 g/cm3,弹性模量E=210 GPa。模拟钻柱材料选用与钢材有相似应力-应变曲线的ABS工程塑料,密度ρ′=1.10 g/cm3,弹性模量E′=2.30 GPa,则密度和弹性模量的相似比为cρ≈0.140、cE≈0.011。
2.3 应用相似准则确定试验参数当井筒内径和钻具结构确定时,最关键的试验参数是钻杆的转速ω和钻压P,通过调节这2个参数,可以改变钻柱的运动状态[13]。由上述的相似指标方程可得到模拟试验和实际工况关于转速ω和钻压P 2个关键参数的对应关系为:

将几何相似比(cl≈1∶10)和物理相似比(cρ≈0.140、cE≈0.011)代入式(8)和式(9)中,得到试验参数和现场参数的对应关系为cω=2.80、cP=1/9 130。现场钻压为50~220 kN,现场转速为20~110 r/min,根据相似比可以得到试验钻压为5~25 N,试验转速为50~300 r/min。由此可得到结论:当试验转速是现场转速的2.80倍,试验钻压是现场钻压的1/9 130时,模拟现象与现场现象相似,可以通过模拟试验近似呈现钻柱的实际工况。
3 水平受压钻柱试验装置的研制及模 拟方案水平受压旋转钻柱试验装置由钻压系统、旋转系统、井液循环系统、杆柱系统、井下模拟系统和检测系统组成。该试验装置针对整体水平井钻柱展开研究,能够模拟多种井下环境,诸如钻压、转速、扭矩、不规则井底和井壁、径向阻尼和循环井液,可以进行固体和流固耦合的动力学行为研究,也可以进行不同钻压、转速和扭矩条件下的钻柱运动状态的试验研究,为清晰准确地了解分析水平井钻柱的动力学状态提供了可靠有效的试验装置。该试验装置的整体结构如图1所示。

|
| 图1 水平受压钻柱试验装置 Fig.1 Horizontal well drill string test apparatus 1—钻压系统和旋转系统; 2—井液循环系统; 3—杆柱系统; 4—井下模拟系统。 |
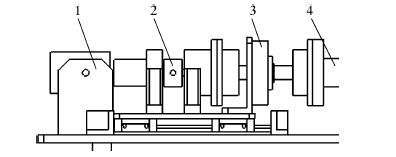
钻压系统(见图2)由1号伺服电机、1号行星轮减速器、丝杠、滑座和轴承座组成。伺服电机与行星轮减速器相连,减速器输出轴通过弹性联轴器与丝杠相连,丝杠上的滑座与平台相连。装置设计中选用行星轮减速器,因为该种减速器无自锁功能,当轴向力过大时,可以对装置起到保护作用,弹性联轴器对钻压系统同样也会起到一定的缓冲保护作用。
伺服电机通过行星轮减速器减速,增加扭矩,带动丝杠旋转,再由滑座带动平台做轴向移动,为钻柱系统施加轴向力,可以模拟水平井钻井过程中的钻压因素。由相似比得到试验钻压5~25 N,试验中将钻压分为5、10、15、20和25 N,对水平钻柱试验装置施加不同钻压,检测钻压对钻柱动力学状态的影响。钻压大小可以通过伺服电机调整。
3.2 旋转系统旋转系统(见图2)由2号伺服电机、2号行星轮减速器、扭矩传感器和钻柱组成。伺服电机与行星轮减速器相连,减速器与扭矩传感器通过对接法兰相连,扭矩传感器通过对接法兰与钻柱相连,扭矩传感器在检测扭矩时,也可以为钻柱系统传递转速和扭矩。

|
| 图2 钻压系统和旋转系统 Fig.2 WOB System and rotating system 1—钻柱;2—对接法兰;3—扭矩传感器;4—2号行星轮减速器;5—2号伺服电机;6—1号伺服电机;7—1号行星轮减速器;8—弹性联轴器;9—丝杠;10—滑座;11—轴承座;12—平台。 |
伺服电机通过行星轮减速器减速,增加扭矩,通过扭矩传感器传递转速和扭矩,带动钻柱旋转,可以模拟水平井钻井过程中钻柱上施加的转速和转矩因素。由相似比得到试验转速50~300 r/min,试验中将转速分为50、100、150、200、250和300 r/min,对水平钻柱试验装置施加不同转速,检测转速对钻柱动力学状态的影响。转速大小可以通过伺服电机调整。
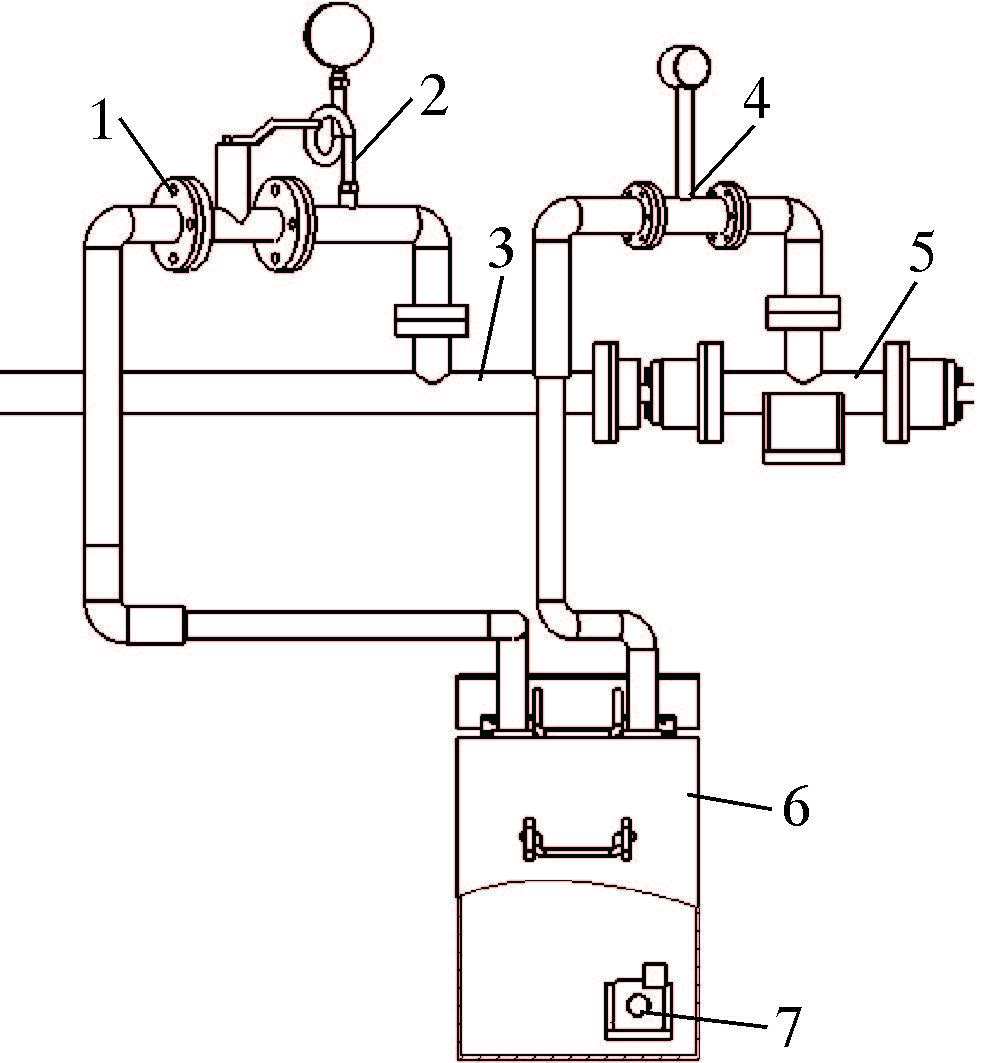
3.3 井液循环系统井液循环系统(见图3)的水箱中内置水泵,流量计通过出水管线和进水转换头接入循环系统,压力表和球阀通过进水管线和有机玻璃管接入循环系统,钻柱和有机玻璃管组成了井液循环通道。
水泵抽汲钻井液,钻井液由出水管线经流量计进入钻柱内部,流至钻柱和有机玻璃管的环形空间后,经压力表和球阀回到水箱,完成井液循环模拟过程。
|
| 图3 井液循环系统 Fig.3 Drilling fluid circulation system 1—球阀; 2—压力表; 3—有机玻璃管; 4—流量计;5—进水转换头;6—水箱;7—水泵。 |
杆柱系统(见图4)是水平受压钻柱试验装置的关键系统,既是钻压系统和旋转系统的主体,同时又构成了井液循环系统,更是检测系统的检测对象。杆柱系统包括钻柱,钻柱之间通过螺纹连接,外部套有有机玻璃管,可以有效模拟水平井中的钻柱。

|
| 图4 杆柱系统 Fig.4 Drill string system 1—电涡流位移传感器; 2—有机玻璃管; 3—钻柱。 |
井下模拟系统见图5,其激振器安装在钻柱底部,通过产生不同频率的激振力模拟不规则井底对钻柱的轴向激振;磁粉制动器与钻柱同轴安装,为钻柱施加一定的反向扭矩,模拟钻柱受到径向阻尼;井筒采用透明的有机玻璃管,能够直观地观察钻柱的运动状态,井筒内壁经过粗糙处理,可以有效地模拟不规则井壁,实现钻柱与井壁之间的碰摩。
|
| 图5 井下模拟系统 Fig.5 Downhole simulation system 1—激振器; 2—压力传感器; 3—磁粉制动器; 4—有机玻璃管。 |
检测系统用于检测钻柱扭矩、径向位置和钻压,通过数据采集卡采集信号,由Labvierw进行界面编程,获得试验数据。检测系统包括1只扭矩传感器、3组9只电涡流位移传感器和1只压力传感器。扭矩传感器通过对接法兰接入旋转系统,可检测钻柱受到的扭矩;3组9只电涡流位移传感器呈x、y方向安装在钻柱3个不同的径向截面上,可检测3个截面上的钻柱径向位置;压力传感器安装在钻柱底部,可检测钻柱所承受的轴向力,即钻压。
4 试验研究 4.1 转速、钻压、扭矩和激振频率等因素的影响在其他试验参数不变的情况下,改变单一因素,并记录传感器的检测数据。通过对2只径向安装的电涡流位移传感器采集信息的耦合处理,确定钻柱的径向振动轨迹。通过轴向安装的电涡流位移传感器的采集信息,确定钻柱纵向振动的运动状态。通过压力传感器的采集信息,确定杆柱与井底的接触情况。通过扭矩传感器的采集信息,确定杆柱的扭转状态。
调节2号伺服电机,对杆柱系统施加转速50、100、150、200、250和300 r/min;调节2号伺服电机,对系统施加扭矩10、15、20、25和30 N·m;调节1号伺服电机,对平台施加钻压5、10、15、20和25 N;调节激振器,对钻柱系统施加激振频率2.5、5.0、7.5、10.0、12.5和15.0 Hz。
研究结果表明,随着转速的增加,径向振动幅度增大,纵向振动有减弱趋势;在其他参数保持一定的情况下,提高钻压有利于减轻钻柱的纵向振动;扭矩变化对钻柱振动影响不大,但与钻柱的粘滑状态相关,增加扭矩有助于克服粘滑现象;在不同参数条件下,存在某一激振频率范围,使得振动幅度加大,钻井过程中应当避开这一频率范围。
4.2 钻井液对钻柱运动状态的影响调节水箱水泵,创造有水和无水2种环境,依次改变转速、钻压、扭矩和激振频率单一因素,对比有水与无水2种情况的试验数据;在有水环境下,调节水泵控制水液流速,记录流速改变对钻柱运动状态的影响。研究结果表明,有水环境相对无水环境更贴近实际工况,因其考虑了流固耦合的影响,有水环境下钻柱运动状态分析较为复杂,试验数据还有待进一步对比研究。
5 结 论(1)基于相似理论和轴承-转子系统动力学推导出的钻柱相似准则,能够有效地指导试验装置的研制和试验研究工作的开展。
(2)基于相似理论研制的水平钻柱试验装置能够通过室内试验的方法探究钻柱的运动机理,并与理论分析相互印证,现场中钻柱承受的钻压并非恒定,有必要改进试验装置,通过模拟试验进一步探究变化的轴向力对水平井钻柱的影响。
| [1] | 林元华,邹 波,施太和.钻柱失效机理及其疲劳寿命预测研究[J].石油钻采工艺,2004,26(1):19-22. |
| [2] | 李方坡,刘永刚,王新虎.钻柱失效原因中的制造因素分析[J].钻采工艺,2013,36(6):86-88. |
| [3] | 范永涛,高德利.底部钻具组合力学特性模拟试验研究[J].石油机械,2013,41(3):80-84. |
| [4] | Yigit A S,Ghristoforou A P.Coupled torsional and ending bending vibrations of activity controlled drill strings[J].Journal of Sound and Vibration,2000,234(1):67-83. |
| [5] | 管志川,靳彦欣,王以法.直井底部钻柱运动状态的试验研究[J].石油学报,2003,24(6):102-106. |
| [6] | Sampaio R,Piovan M T,Lozano G V.Coupled axial/torsional vibrations of drill-strings by means of non-linear model[J].Mechanics Research Communications.2007,34:497-502. |
| [7] | Fernandez M A,Inciarte G,Ramones R.Halliburton-landmark graphics corporation,dynamic analysis of stabilized drilling strings performance in low-dip wells[C]//SPE Latin American and Caribbean Petroleum Engineering Conference,Texas:Society of Petroleum Engineers,2003:12-13. |
| [8] | 范永涛,高德利.底部钻具组合动力学特性模拟试验方法研究[J].石油机械,2013,41(4):6-10. |
| [9] | 管志川,邵冬冬,温欣.水平井眼中旋转钻柱运动特性的试验研究[J].工程力学,2013,30(5):340-345. |
| [10] | 章扬烈.钻柱运动学与动力学[M].北京:石油工业出版社,2001. |
| [11] | 虞烈,刘 恒.轴承-转子系统动力学[M].西安:西安交通大学出版社,2001:51-53. |
| [12] | 徐挺.相似理论与模型试验[M].北京:中国农业出版社,1982:49-56. |
| [13] | 魏文忠,管志川,刘永旺.直井眼钟摆钻具纵向振动特性的试验研究[J].中国石油大学学报:自然科学版,2007,31(2):64-68. |



