2. 重庆前卫海洋石油工程设备有限责任公司
2. Chongqing Qianwei Offshore Petroleum Engineering & Equipment Co., Ltd.
0 引言
密封结构作为水下井口连接器的重要组成部分,其性能直接决定采油树工作的安全性与可靠性[1]。水下采油树工作过程中面临着复杂的操作工况,如安装、生产、完井和修井等,同时还有恶劣的环境工况,包括波浪、海流、钻井船的漂流及隔水管的张力和弯矩等,这些因素直接影响密封结构的密封性能,密封一旦失效,将造成井口连接器无法正常工作,严重时还将导致灾难性事故[2, 3, 4, 5, 6]。
目前国内有关金属密封圈的研究不多,处于起步阶段。如饶松海[7]对VX形金属密封圈的密封原理进行了分析与试验,分析了密封圈的受力与变形;李志刚等[8]对密封面角度进行了改进,提出了复合式密封结构;王川等[9]对水下井口连接器在不同工况下的结构性能进行了研究,分析了不同工况下密封圈的密封性能。国外研究起步较早,已经掌握了先进的密封技术,如M.Badicioiu等[10]运用理论与试验相结合的方式对金属密封圈的密封性能进行了研究。目前关于水下井口连接器密封性能分析的研究[11]具有一定的局限性,主要表现在:①主要针对预紧或生产单一工况进行分析,没有针对井口连接器在多种复杂工况下的性能分析;②在进行井口连接器弯矩工况分析时,大多采用二维轴对称模型,将弯矩转化为力的方式施加,无法有效地模拟弯矩工况下各部件的相互作用,影响了计算结果的准确性。
为此,笔者以井口连接器为研究对象,运用Abaqus手动编写inp程序的方法进行有限元计算,首先分析安装预紧工况井口连接器密封圈接触应力及径向压缩量等参数影响规律,随后研究生产工况接触应力、介质内压、毂面力和本体井口相对间隙等参数相互影响规律,最后分析完井/修井工况接触应力的变化规律,以期为其他类型井口连接器的密封性能研究提供参考。
1 井口连接器结构及工作原理如图 1所示,井口连接器主要由本体、壳体、驱动环、卡爪、金属密封环、解锁活塞、锁定活塞及底板组成。连接器安装时,液压油通过锁定活塞带动驱动环向下运动,通过驱动环斜面挤压卡爪斜面,从而锁紧本体与井口。通过本体与井口的密封槽斜面对金属密封圈轴向预紧,从而完成金属密封圈的预紧密封。锁紧后,为了防止连接器在振动和外载等作用下发生解锁,要求卡爪与驱动环的接触面具备自锁能力。井口连接器的自锁能力与接触面的摩擦因数无关,只与接触面的摩擦角有关。
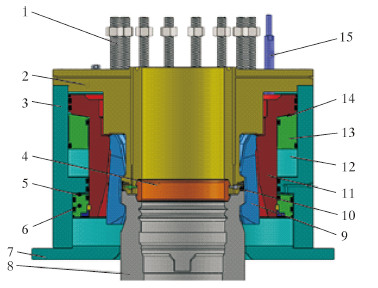
|
| 图 1 井口连接器结构示意图 Fig.1 Structural schematic of wellhead connector 1—上部设备连接螺栓;2—本体;3—壳体;4—金属密封圈;5—锁定密封腔;6—锁定活塞;7—底板;8—井口;9—锁块;10—金属密封圈固定机构;11—驱动环;12—二次解锁密封腔;13—二次解锁活塞;14—首次解锁密封腔;15—位置指示器。 |
井口连接器工况复杂,根据环境要求和作业内容,具体分为以下3个工况:工况1为安装预紧模式;工况2为生产模式;工况3为完井/修井模式。该井口连接器的主要参数为:额定工作压力34.5 MPa,水下井口直径476.25 mm,水下作业深度500 m,最大锁定液压20.7 MPa。
2 井口连接器数学模型 2.1 有限元模型井口连接器整套设备部件复杂,为了有限元计算方便,需对模型进行简化。根据力平衡准则,液压油作用于驱动环的推力等于本体在轴线方向上的受力,因此,在分析井口连接器的密封性能时,仅取本体、金属密封圈和井口为分析对象。连接器简化模型如图 2所示。
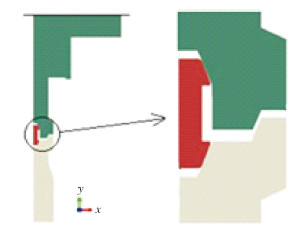
|
| 图 2 井口连接器简化模型 Fig.2 Simplified model of wellhead connector |
图 3给出了本体、金属密封圈和井口的网格模型。为保证计算精度,3个部件全部采用四边形轴对称单元CAX4R进行分析。金属密封圈采用304不锈钢,弹性模量195 GPa,泊松比0.3,屈服强度302 MPa。在本体上部建一解析刚体,对解析刚体参考点施加向下的强制位移来模拟锁紧过程,并通过输出轴向接触力得到轴向位移所需的轴向预紧力。分别在解析刚体与本体之间、本体与井口之间、金属密封圈与本体之间、金属密封圈与井口之间建立面-面接触,采用拉格朗日法描述4对接触间的法向行为,用罚函数定义切向行为,将摩擦因数设为0.15。井口底面在x、y和z方向上施加固定约束。
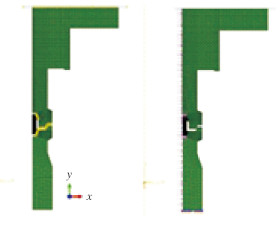
|
| 图 3 连接器有限元模型 Fig.3 Finite element model for wellhead connector |
以上模型适用于工况1与工况2,工况3由于受弯矩的影响,需要通过Abaqus的手动inp编程,将简化后的2D模型转化成3D模型,如图 4所示。工况3模型的边界条件与工况1相同。模拟施加弯矩载荷条件时,在本体上端面圆心处施加逆时针方向弯矩,弯曲弧度为0.015 rad。

|
| 图 4 井口连接器3D有限元模型 Fig.4 3D finite element model of wellhead connector |
安装预紧模式下,通过文献[12]中的公式
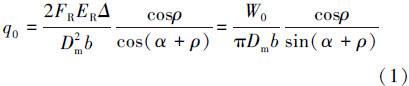
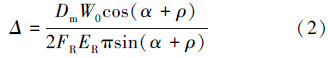
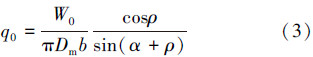
由式(2)和式(3)可知,金属密封圈的径向压缩量Δ与轴向预紧力W0成正比,密封圈接触面的接触应力q0与轴向预紧力W0也成正比。
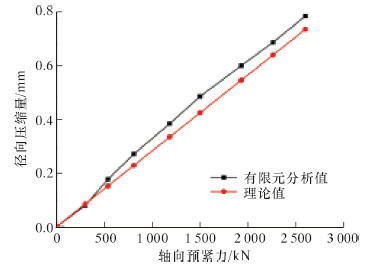
3 结果分析与讨论 3.1 安装预紧工况通过Abaqus软件得到有限元分析结果和公式推导理论值的对比曲线,如图 5所示。由图可知,有限元分析值与理论值误差较小,且有限元分析值大于理论值。产生此种情况的原因是在理论计算时,井口连接器的金属密封圈被简化为刚体,即密封圈的接触中径是定值,而实际情况是密封圈的密封中径是变化的,且随着轴向预紧力的增大密封圈发生了弹塑性变形,密封圈与本体的密封接触从开始的环线型接触变成环带型接触。另外,图中径向压缩量随轴向预紧力增加而增大,而在1 500 kN后直线上升较缓,这是因为在开始阶段发生了弹性变形,到达屈服强度时材料发生了塑性变形,因此径向压缩量的增长率变小。
|
| 图 5 径向预紧压缩量与轴向预紧力关系曲线 Fig.5 Relation curve of the radial compression and axial preload |
在工况1中,金属密封圈的接触应力云图如图 6所示。随着本体向下预紧,金属密封圈受到本体与井口轴向预紧作用,接触面的接触应力从两端逐渐向中间移动,预紧初期最大的接触应力出现在金属密封圈下表面,这是因为在预紧过程中金属密封圈的下表面最先与井口接触,随后才与本体的锥形表面接触,且井口底面约束了6个自由度。

|
| 图 6 密封圈预紧状态接触应力云图 Fig.6 Contact stress of gasket ring in preloading condition |
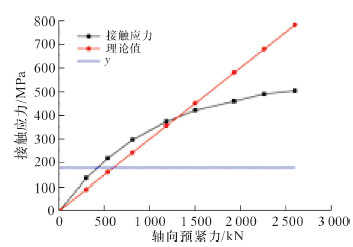
图 7是密封圈接触应力有限元分析值与公式(3)理论值对比曲线。图中y值为预紧密封比压。由GB 150—2010可知,垫片系数为6.5,密封比压y为179.3 MPa,接触应力大于密封比压,即金属密封圈满足密封要求。图中接触应力的理论值随轴向预紧力呈线性增加,接触应力有限元分析值呈非线性增加,说明接触应力增加的速度变缓。产生接触应力非线性增加的原因在于本体与金属密封圈接触的初始状态为环线型接触,随着轴向预紧载荷的增大,密封接触面积增大,成环带型接触。另外,有限元分析值比理论值先达到密封比压,而后随着轴向预紧力的增加,理论值大于有限元分析值,原因是预紧初期密封圈接触中径小于理论密封中径,而后接触中径大于理论中径。
|
| 图 7 接触应力与轴向载荷关系图 Fig.7 Relation of contact stress and axial load |
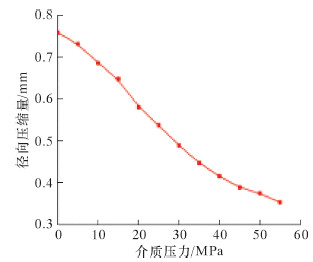
在生产工况下,井口连接器主要受到内部介质流体的作用。根据标准ISO 13628-4,整个系统应能承受1.5倍额定工作压力。如图 8所示,在介质压力开始增大时,密封圈径向压缩量最大,随着介质压力的增大,径向压缩量逐渐减小,密封圈逐渐发挥本身的回弹能力。在介质压力达到最大时,金属密封圈还存在径向压缩量。可以看出预紧状态时压缩量没有完全释放,金属密封圈具有密封性。
|
| 图 8 径向压缩量与介质压力关系曲线 Fig.8 Relation of radial compression and operating pressure |
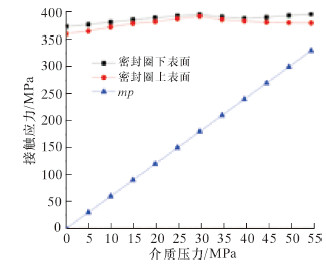
图 9为接触应力与介质压力关系图。由图可知,经过预紧状态后,随着内部介质压力增大,接触应力呈缓慢增大趋势。若持续增大介质压力,mp直线将与密封圈上、下表面的直线相交,在相交点之后密封圈将不再满足密封条件,而交点横坐标值即为密封圈所能承受的最大介质压力。另外,密封圈下表面的接触应力大于上表面,这是因为在井口连接器介质压力增大过程中发生了翘曲变形。
|
| 图 9 接触应力与介质压力关系曲线 Fig.9 Relation of contact stress and operating pressure |
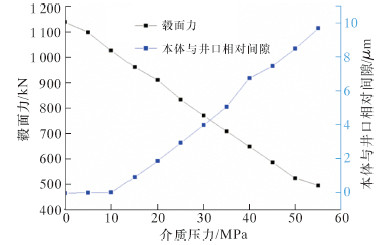
图 10是毂面力和井口本体相对间隙与介质压力关系图。由图可知,在生产工况下,随着内部介质压力的增加,井口与本体接触面的毂面力逐渐减小,本体与井口的相对间隙逐渐增大。产生这种情况的原因是,由于内部介质流体作用于金属密封圈的径向方向,引起接触面产生轴向载荷分量,且流体作用于连接器内部流道也形成轴向载荷,由此形成的2个轴向载荷使得井口与本体具有相对分离的趋势,从而使井口与本体接触面的毂面力减小且相对间隙增大。
|
| 图 10 毂面力和井口本体相对间隙与介质压力关系图 Fig.10 The effect of operating pressure on hub surface force and the hub surface separation distance |
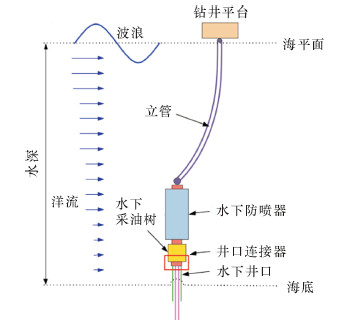
水下井口连接器在钻完井和修井工况下,不但要承受张力管内部介质流体的压力,还受到弯矩的作用,如图 11所示。
|
| 图 11 井口连接器弯矩示意图 Fig.11 Schematic of wellhead connector bending moment |
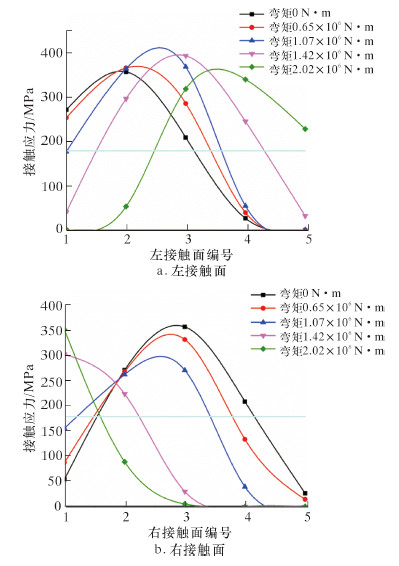
图 12为5种弯矩条件下金属密封圈左、右接触面(图 13)接触应力变化曲线。图中平行于X轴的直线为金属密封圈的密封比压。从图 12a可以看出,弯矩曲线的波峰对应的横坐标随着弯矩的增大而逐渐向右移动,表明随着弯矩的增大,接触面的密封中心逐渐向外径方向(即编号增大方向)移动。由内径至外径方向,接触面的接触应力在5种弯矩载荷下均大于密封比压。弯矩曲线与密封比压直线相交点之间的长度为密封圈的有效接触宽度,且由于密封圈的接触宽度先减小后增大,导致最大接触应力先增大后减小。从图 12b可以看出,由于对井口连接器施加了逆时针方向的弯矩,随着弯矩的增大,密封圈右端接触面接触应力最大值逐渐向左端移动,接触面的接触中心逐渐向内径方向(即编号减小的方向)移动。同样,弯矩曲线与密封比压直线2个交点之间的有效接触宽度先增大后减小。
|
| 图 12 弯矩条件下金属密封圈接触应力图 Fig.12 Contact stress of the gasket ring under bending moment |
|
| 图 13 密封圈节点编号 Fig.13 Node number of the gasket ring |
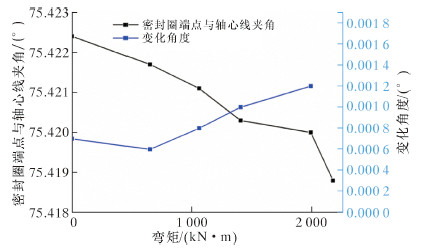
随着弯矩的增大,金属密封圈发生了翘曲变形,如图 14所示。图中左边Y轴为密封圈的上表面端点与金属密封圈的中心线的夹角,由于井口连接器施加的逆时针弯矩,夹角随着弯矩的增大逐渐减小,且图中蓝色线为夹角变化值,从图中可看出变化最大值为0.001 2°,最小值为0.000 6°。
|
| 图 14 翘曲角度变化图 Fig.14 Buckling angle variation |
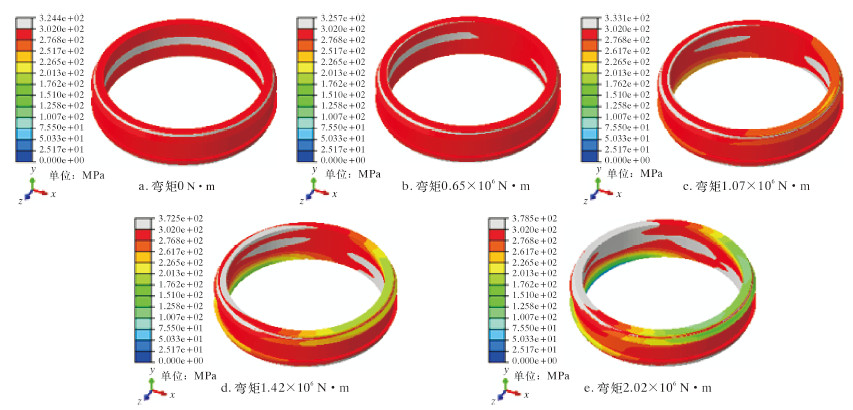
图 15为5种弯矩载荷下金属密封圈的应力云图。从图可看出,金属密封圈左端应力随着弯矩的增大而增大。金属密封圈的材料屈服强度为302 MPa,图中灰色区域为发生屈服的区域。在预紧阶段,屈服区域出现在金属密封圈的上、下接触面及内表面中间区域。在0.65×106 N·m弯矩条件下,密封圈接触应力增大,最大值为325.7 MPa,密封圈右端屈服区域减小,左端增大;在1.07×106 N·m弯矩条件下,密封圈左端接触应力增大,最大值为333.1 MPa,密封圈右端上表面接触发生了回弹,下表面接触存在屈服;在1.42×106 N·m的弯矩条件下,接触应力最大值为372.5 MPa,密封圈左端上表面屈服区域增大,右端下表面还存在屈服现象,右端上表面接触应力减小;在弯矩2.02×106 N·m弯矩条件下,密封圈左端下表面屈服消失,接触应力减小,上表面屈服面积增大,右端下表面存在屈服现象。图 15的应力云图及图 14的曲线表明,即使金属密封圈发生大面积的屈服现象,但其仍然能够保证井口连接器在水下的密封性。但为了保证水下密封的安全性,金属密封圈只能使用1次。
|
| 图 15 金属密封圈应力云图 Fig.15 The stress distribution of the gasket ring |
(1)安装预紧工况时,径向压缩量与轴向预紧载荷关系密切,密封圈接触面的接触应力随着轴向预紧载荷的增大而增大,且能够实现密封圈的有效密封。
(2)生产工况时,金属密封圈径向压缩量随着内压的增大而减小,密封圈发生了回弹,表明其具有自紧性。在内部流体压力影响下,密封圈的上、下接触面的接触应力不均匀,密封圈发生了翘曲变形,且受内压作用时,本体与井口毂面力减小,井口与本体具有分离的趋势。
(3)完井与修井工况时,在不同弯矩条件下,金属密封圈左、右接触面的接触应力均超过密封比压,接触面的中心和有效接触宽度均发生变化。井口连接器在承受2.02×106 N·m弯矩条件时,密封圈接触面内、外径方向均发生屈服,密封圈仍然具有密封性。
| [1] | Larson E D,Keosoff K G.Marginal subsea development with existing subsea trees[R].OTC 16533,2004. |
| [2] | 吴时国,袁圣强.世界深水油气勘探进展与我国南海深水油气前景[J].天然气地球科学,2005,16(6):693-699,714. |
| [3] | Kelly T P,Strauss R H.Agbami field development: Subsea equipment systems,trees,manifolds and con- trols[R].OTC 19919,2009. |
| [4] | Lonnes S.Successful subsea interventions in North Sea Beryl Field[R].OTC 125258,2009. |
| [5] | Stright S.Regeneration of first-generation subsea fields:The challenges of new wells in old infrastructure[R].SPE 151202,2012. |
| [6] | Buitrago J,Krishnan V R,Sommerfield P M.Fatigue assessment of subsea tree connectors and wellheads[C]. International Conference on Ocean,Offshore and Arctic Engineering,Rotterdam,OMAE2011-49853,2011. |
| [7] | 饶松海.VX钢圈密封原理探索[J].中国海洋平台,1998,13(3):30-33,29. |
| [8] | 李志刚,运飞宏.水下连接器密封性能分析及实验研究[J].哈尔滨工程大学学报,2015,36 (3):389-393. |
| [9] | 王川,朱宏武.螺栓连接式水下井口连接器结构性能分析[J].石油机械,2013,41(12):48-52. |
| [10] | Badicioiu M,Teodoriu C.Sealing capacity of API connections-theoretical and experimental results[R].SPE 106849,2007. |
| [11] | Kurokouchi S,Okabe M,Morita S.Taper-seal type metal sealing system and available applications[J]. Applied Surface Science,2001(169/170):799-802. |
| [12] | 陈晓芳,赵宏林.水下卧式采油树井口连接器VX钢圈力学特性分析[J].石油机械,2014,42(8):62-67. |



