0 引言
随着我国对环境和能源问题的重视,天然气(LNG)作为一种清洁能源逐步受到人们的关注和重视。绕管式换热器[1, 2]的换热管是螺旋形状,其结构紧凑,换热效率高,耐高压,可实现多种介质的传热。绕管式换热器的安全运行直接影响到整个LNG工厂。在横向流的作用下,缠绕管管束很容易振动。振动会引起换热管的碰撞、折流板切割换热管、管与管板连接处的泄漏、换热管的疲劳破坏以及噪声等。只有认识缠绕管的振动机理,才能有效合理地控制振动,从而使绕管式换热器安全运行。
关于缠绕管的振动,美国阿贡实验室的S.S.Chen[3]做过缠绕管在横向水流冲刷下的试验。Wang Lin等[4]用数值计算的方法研究了缠绕管在运动约束和简谐激励下的动力特性。Yan Ke等[5]用有限元法研究了螺旋锥的振动特性。薄涵亮等[6]通过试验研究得到缠绕管管束与直管管束之间存在一些差别。刘瑞兰等[7]通过试验测定了缠绕管流体力的系数,了解到缠绕管管束在横向气流激励下的响应。国内外对流体诱发振动也制定了一些相应的标准,如美国管式换热器制造商协会(TEMA)标准[8]、ASME锅炉与压力容器规范第三篇附录N-1300[9, 10]、美国焊接研究委员会公报(WRC Bulletin)372号[11]以及我国的GB/T151—2014附录C[12]。这些标准的制定对控制换热器振动起到了很大的作用。
由于国内外对LNG缠绕管的振动研究较少,所以笔者通过数值模拟的方法对LNG绕管式换热器中单根缠绕管进行绕流分析。因国内外对圆柱体绕流的问题研究较多,所以笔者借鉴圆柱体绕流的方法,研究LNG缠绕管在雷诺数、管径和螺旋角的不同参数组合下,压力系数、脉动升力系数、漩涡脱落频率和斯特罗哈数的变化规律,从而得到缠绕管的绕流特性。
1 数值模拟 1.1 基本方程采用Fluent6.3商业软件进行模拟,对不可压缩黏性流体,在直角坐标系中,可用N-S方程来描述,连续性方程和动量方程为:
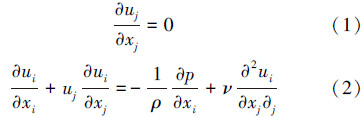
图1为换热器缠绕管剖面图。由图可知,缠绕管与圆柱的明显区别在于缠绕管的剖面图为椭圆。管径和螺旋角的变化使得椭圆截面的尺寸也发生变化。由文献[11]可知,在横向流作用下单根管的主要振动机理应考虑漩涡脱落激振。笔者研究的是单根缠绕管的绕流问题,其计算模型如图2所示,计算区域长800 mm、宽600 mm。椭圆中心距速度入口200 mm,距离壁面300 mm。将雷诺数换算成流速,因此将进口设为速度进口,出口设为自由出口,椭圆边界和上、下边界设为壁面。

|
| 图 1 缠绕管剖面图 Fig.1 Cross sectional view of the pipe |

|
| 图 2 单根缠绕管绕流计算模型 Fig.2 Calculation model of flow around a single spiral pipe |
用于LNG绕管式换热器的缠绕管管径D=8~25 mm,螺旋角α=5°~20°。在LNG中绕管式换热器壳程流体的流速较小,雷诺数Re的变化范围为200~1 000。
1.3 离散方式及网格划分在Fluent中设置非定常流动对缠绕管绕流进行分析。非定常流动的格式设置为一阶隐式,压力和速度耦合采用Simpliec算法;为了在保证精度的前提下加快收敛速度,对压力的离散采用二阶格式,对动量的离散采用二阶迎风格式。各参数的残差收敛标准为1×10-5。计算时间步长设为0.1 s,时间步数设为1 000,即迭代时间为100 s,每个时间步长迭代30次。当升力系数曲线呈现周期性变化时,可以保证迭代的收敛。
对计算区域采用非结构三角形网格进行网格划分,并在椭圆周围进行网格加密,如图3和图4所示,通过网格检测工具能得到很高质量的网格。文献[14, 15, 16, 17, 18, 19]也是用这种方法进行模拟,得到的数据与试验数据吻合。

|
| 图 3 计算区域网格划分 Fig.3 Mesh generation in calculation area |

|
| 图 4 网格加密 Fig.4 Mesh refinement |
缠绕管边界层分离点的位置随着螺旋角、管径和雷诺数的变化而变化。下面分别讨论螺旋角、管径和雷诺数对压力系数的影响。鉴于篇幅所限,如考虑螺旋角的影响时,则管径和雷诺数保持不变。对管径和雷诺数分析时也采用这种方法。压力系数的变化曲线范围是θ=0°~360°,并且变化曲线关于θ=180°对称,因此选取θ=0°~180°之间的曲线进行分析。根据图5边界层分离现象可知,θ表示壁面上某点和O点的连线与OA的夹角。

|
| 图 5 边界层分离现象示意图 Fig.5 Schematic of boundary layer separation |
当Re=200和D=16 mm时,不同螺旋角的缠绕管表面压力系数的变化情况如图6所示。由图可见,在θ=75°左右压力系数最小;在θ=130°左右出现边界层分离现象。螺旋角越大,压力系数的最小值越小,且分离点后移。

|
| 图 6 不同螺旋角缠绕管表面压力系数 Fig.6 Surface pressure coefficient of spiral pipe with different helix angles |
由图7可知,当Re=600、螺旋角α=10°时,曲线同样经过一个增速减压的过程,在θ=75°左右压力系数最小;在θ=125°左右出现边界层分离现象。管径越大,压力系数的最小值越小,且分离点前移。

|
| 图 7 不同管径缠绕管表面压力系数 Fig.7 Surface pressure coefficient of spiral pipe with different pipe diameters |
不同雷诺数缠绕管表面压力系数如图8所示。由图可知,当D=16 mm、α=15°时,曲线经过一个增速减压过程,在θ=75°左右压力系数最小;在θ=120°左右出现边界层分离现象。随雷诺数增大,压力系数的最小值越大,且分离点后移。

|
| 图 8 不同雷诺数缠绕管表面压力系数 Fig.8 Surface pressure coefficient of spiral pipe with different Reynolds number |
由文献[20]可知,当Re≥40时,圆管背后两侧产生交替漩涡。交替脱落的漩涡会在圆管上产生横向交变作用力,迫使圆管振动。脉动升力系数频率即为漩涡脱落频率。通过模拟得到的缠绕管脉动升力系数的频率即为漩涡脱落的频率。
捷克物理学家斯特劳哈尔通过试验得到从单管表面脱落的漩涡频率计算公式:

斯特劳哈尔数是分析漩涡脱落频率很重要的基本数据,为此许多科研人员做了大量的试验。目前使用最广泛的是陈延年[21]根据声共振得到的(当300≤Re≤2×105时)斯特劳哈尔数在0.2左右。由公式(3)可知,Sr=fsd/v0。
当漩涡周期性脱落时,脉动升力频率等于漩涡脱落频率。此时,求出脉动升力频率,就能求出漩涡脱落频率fs,从而求出Sr。螺旋角对脉动升力系数的影响如图9所示。由图可以看出,螺旋角对漩涡脱落频率影响不大,管径D和雷诺数Re对其影响较大。

|
| 图 9 螺旋角对脉动升力系数的影响 Fig.9 The effect of helix angle on the fluctuating lift coefficient |
当管径D=8 mm,雷诺数Re分别为200、400、600、800和1 000时,升力系数-时间历程曲线如图10所示。从图可以看出,漩涡脱落频率随着雷诺数的增加而增加,脉动升力系数幅值随着雷诺数的增加而减小,并且逐渐趋于稳定。当雷诺数增加到800、1 000时,升力系数的波动逐渐减小直至趋于稳定,并且Re=1 000趋于稳定的时间比Re=800趋于稳定的时间短。此过程为稳态流动过程,因为管后两侧同时产生1对漩涡,此时缠绕管上不会产生横向交变作用力。圆管背后两侧产生1对稳定的漩涡,此时15≤Re<40。而D=8 mm的缠绕管管后产生1对稳定漩涡时,Re可以取1 000,即缠绕管管后要产生1对稳定的漩涡要比圆柱的流速更高。因此,螺旋管管后要产生稳态流动的流速比圆管大。

|
| 图 10 管径D=8 mm,不同雷诺数下升力系数-时间历程曲线 Fig.10 The lift coefficient-time history plot under different Reynolds numbers when pipe diameter is of 8 mm |
当管径D=12 mm,Re分别为200、400、600、800和1 000时,升力系数时间历程曲线见图11。从图可见,漩涡脱落频率随着管径的增加而减小,随着雷诺数的增加而增加;随着雷诺数的增加,脉动的升力系数波动的幅值减小,且有趋于稳定的趋势;管径越大,脉动升力系数波动的幅值也就越大。

|
| 图 11 管径D=12 mm,不同雷诺数下升力系数-时间历程曲线 Fig.11 The lift coefficient-time history plot under different Reynolds numbers when pipe diameter is of 12 mm |
图12和图13分别为漩涡脱落频率和斯特劳哈尔数与雷诺数的关系。从图中可以看出,当200≤Re≤1 000时,漩涡脱落频率随Re的增大而增大,随管径的增大而减小。随着Re的增大,斯特劳哈尔数先增大后减小,且随着管径的增大而减小。斯特劳哈尔数在0.150~0.185之间,比圆管的Sr小。因此,缠绕管漩涡脱落频率比圆管的小。

|
| 图 12 漩涡脱落频率与雷诺数的关系 Fig.12 The relation of vortex shedding frequency and Reynolds number |

|
| 图 13 斯特劳哈尔数与雷诺数的关系 Fig.13 The relation of Strouhal number and Reynolds number |
笔者通过数值模拟方法对绕管式换热器中单根缠绕管在Re=200、400、600、800和1 000,螺旋角分别为5°、10°、15°和20°,管径D=8、12、16和20 mm的参数组合下,研究压力系数、脉动升力系数、漩涡脱落频率和斯特劳哈尔数的变化规律,得到如下结论。
(1)表面压力系数在θ=75°左右最小,在θ=120°~130°时,发生边界层分离。
(2)当螺旋角和雷诺数增大时,边界层分离点位置向后移动;当管径增大时,边界层分离点位置向前移动。
(3)螺旋角对漩涡脱落频率的影响不大,漩涡脱落频率随雷诺数的增加而增加,随管径的增加而减小。
(4)随着雷诺数的增加,斯特劳哈尔数先增加后减小,且最大斯特劳哈尔数Sr=0.185,因此缠绕管漩涡脱落频率小于圆管的脱落频率。
| [1] | 张周卫,李跃,汪雅红,等.低温液氮用系列缠绕管式换热器的研究与开发[J].石油机械,2015,43(6):117-122. |
| [2] | 张周卫,薛佳幸,汪雅红,等.LNG系列缠绕管式换热器的研究与开发[J].石油机械,2015,43(4):118-123. |
| [3] | Chen S S.Tube vibration in half-scale sector model of helical tube steam generator[J].Journal of Sound and Vibration,1983,91(4):539-569. |
| [4] | Wang Lin,Ni Qiao,Huang Yuying.Dynamical behaviors of a fluid-conveying curved pipe subjected to motion constraints and harmonic excitation[J].Journal of Sound and Vibration,2007,306(3):955-967. |
| [5] | Yan Ke,Ge Peiqi,Bi Wenbo,et al.Vibration characteristics of fluid-structure interaction of conical spiral tube bundle with FEM[J].Journal of Hydrodynamics,2010,22(1):121-128. |
| [6] | 薄涵亮,宋志坚,沈时芳,等.螺旋管管束流体诱发振动的实验研究[J].核动力工程,1993,14(3):232-237. |
| [7] | 刘瑞兰,沈时芳.在横向气流激励下螺旋管管阵流体力系数的实验测定[J].应用力学学报,1994,11(1):76-81. |
| [8] | Standards of TEMA[S].9th ed,2007. |
| [9] | ASME boiler and pressure vessel code[S].SectionⅢ,Appendix N(N-1300 series),1995. |
| [10] | ASME boiler and pressure vessel code[S].An International Code,SectionⅢ,Division 1-Appendices,Rules for Construction of Nuclear Power Plant Components,2010. |
| [11] | Sandifier J B.Guidelines for flow induced vibration prevention in heat exchangers[R].WRC Bulletin 1992,372:1-27. |
| [12] | GB/T 151-2014 热交换器[S].北京:中国标准出版社,2015. |
| [13] | Pettigrew M J.Flow-induced vibration:Recent findings and open questions[J].Nuclear Engineering and Design,1998,185(2):249-276. |
| [14] | 杨烁,吴宝山.二维圆柱绕流数值模拟[J].中国造船,2007,48(增刊1):533-540. |
| [15] | 吴言超,陆晓峰.低雷诺数圆柱绕流特性的数值模拟[J].大庆石油学院学报,2011,35(5):73-78. |
| [16] | 金思宇,张治国,吴琦.流速对圆柱绕流旋涡脱落的分析[J].化学工程与装备,2012(12):48-52. |
| [17] | 莫同鸿,段文益,伍远平,等.气旋浮高效油水分离器试验研究[J].石油机械,2010,38(12):5-8. |
| [18] | 鞠少栋,陈国明,盛磊祥.波状圆柱绕流流场CFD分析[J].石油机械,2009,37(3):35-37. |
| [19] | 毕继红,余华军,任洪鹏.静止方柱和圆柱绕流的二维数值分析[J].三峡大学学报:自然科学版,2012,34(1):41-45. |
| [20] | 聂清德,谭蔚.管壳式换热器流体诱发振动[M].北京:中国石化出版社,2013. |
| [21] | Chen S S.Flow-induced vibration of circular cylindrical structures[M].New York:Hemisphere Publishing,1987. |




