2. 重庆前卫海洋石油工程设备有限责任公司;
3. 长江大学机械工程学院
2. Chongqing Qianwei Offshore Petroleum Engineering & Equipment Co., Ltd.;
3. School of Mechanical Engineering, Yangtze University
0 引 言
SCM(水下控制模块)是采油树的水下控制中心,其安装及维护是整个水下系统正常运行的有力保障。因此,在安装、拆除或维修SCM时,下放和回收工具必不可少。国内关于海洋水下控制模块的研究仍处于起步阶段且多限于理论[1]。目前的SCM都无需安装指导,只要在水下遥控机器人(ROV)辅助下用简单的起重钢丝就能安装和维修[2]。SCM作为单独的模块,必须由单独的回收和下放工具即SCMRT(SCM下放工具)来实现[3],而整个SCMRT最关键的部分是锁紧机构。SCMRT与SCM通过SCMRT上锁紧机构进行连接,在SCMRT锁紧至SCM的过程中,SCMRT上锁块应作为主要研究对象,对其进行受力分析,判断其锁紧过程中是否发生屈服。因此,笔者利用ABAQUS有限元软件对SCMRT的锁紧机构在锁紧工况中所受到的应力进行分析,以期得到满足实际强度要求的锁块结构。
1 锁紧机构接触分析的理论模型 1.1 锁紧机构简介锁紧机构是SCM下放装置的核心部件。当对SCM进行安装时,主要应用ROV进行监测,利用下放装置中的锁紧机构将SCM锁紧下放到安装基座附近,并利用ROV操作手把SCM准确地安装在基座上。锁紧机构由锁紧外壳、锁块、锁紧指示器、ROV把手和锁紧机制(锁紧滑块、锁紧连杆、锁紧曲柄和ROV驱动杆、ROV接口)组成。锁紧机构的优劣直接关系到整个下放工具的功能是否能够实现,因此要重点分析。
1.2 锁紧过程中的接触问题锁紧机构的锁紧和解锁过程应简单易行,能够保证操作的顺利完成;锁紧机构锁紧后,要保证锁块在SCM内稳定可靠,不会上、下移动而发生失效;锁紧机构不仅要有足够的强度和刚度,而且要有足够的韧性,这是因为锁紧机构要承受SCMRT和SCM的所有重力。
锁紧机构有液压式和机械式2种。机械式锁紧机构采用安装机具直接推动安装的形式,操作方便,结构形式简单,因此,笔者采用机械式锁紧机构。锁紧时,锁紧滑块在锁紧连杆作用下向下移动,锁块在锁紧滑块的挤压作用下向外滑动,进入SCM锁槽,实现锁紧[4]。在锁紧过程中,锁块与锁紧滑块的接触面上会发生挤压,产生应力集中,这也是笔者的主要研究内容。
1.3 接触分析的基本理论有限元分析中的结构非线性分析主要可分为状态(接触)非线性、几何非线性和材料非线性3种类型[5]。锁紧机构运行时,锁紧滑块沿轴向下移并挤压锁块,锁块沿径向运动,其与SCM的作用会使得锁块产生滑移,这属于典型的接触非线性问题。
锁块是锁紧机构的主要受力部件。对锁块主要考虑锁紧角度、解锁角度以及锥面角度问题。
1.3.1 锁紧角度锁紧角度定义为锁紧滑块对锁块进行锁紧时,锁块内侧上斜面与锁块移动方向的夹角。
当锁块内部上斜面倾角的正切值小于或者等于斜面上的锁块与锁紧外壳之间的摩擦因数μ时,就会形成自锁,此时无论锁紧滑块向下的推力有多大,锁块都无法向锁槽内滑动。因此在考虑锁块与锁紧滑块接触面的角度时,要避免发生自锁,否则进行锁紧操作时锁紧滑块将撑不开锁块,无法将锁块挤入锁槽而造成锁紧失败。锁块锁紧过程及锁紧面受力分析图如图 1所示。

|
| 图 1 锁紧面受力分析 Fig. 1 Forces on the locking surface |
图 1中:α为锁紧面与锁块移动方向的夹角;F1为锁紧滑块所受到的推力;F1n为F1分解得到的锁紧滑块对锁块的正压力;F1t为F1分解得到的锁紧滑块对锁块沿斜面方向的力;F1nx为F1n分解得到的沿锁块移动方向的分力;F1ny为F1n分解得到的锁块所受向下的正压力。
若锁紧滑块能够沿轴向向下移动,且锁块能够沿径向向外滑动,则须同时满足:

式中:μ1为锁紧滑块和锁块之间的摩擦因数,μ2为锁块与锁紧外壳之间的摩擦因数,整理得:

摩擦副为钢铁与钢铁时,摩擦因数为0.15[6],因此得到:
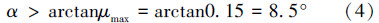
即α只要大于8.5°就不会发生自锁。
1.3.2 解锁角度解锁角度即锁紧套筒在对锁块进行解锁时,锁块外侧上斜面与锁块移动方向的夹角。
进行解锁操作时,由锁紧连杆将锁紧滑块向上拉升,当锁紧滑块位于锁紧外壳上方,锁块的约束消除,SCM锁槽内上部斜面对锁块的作用使其离开锁紧位置。锁块的解锁受力分析图如图 2所示。

|
| 图 2 解锁面受力分析 Fig. 2 Forces on the unlocking surface |
图 2中:β为解锁面与锁块移动方向的夹角;F2为锁块受到的拉力,即锁紧壳体锁槽底部对锁块向上的推力;F2t为F2分解得到的沿锁槽斜面方向的力;F2n为F2分解得到的锁块对SCM的正压力;F′2n为SCM对锁块的反作用力;F′2nx为F′2n分解得到的锁块沿水平方向上的力;F′2ny为F′2n分解得到的锁块对锁紧壳体的压力。
同理,为防止在锁紧壳体与锁块接触面上出现自锁现象,须同时满足:

整理得:
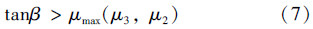
式中:μ3为SCM与锁块之间的摩擦因数,取最大值0.15,计算得到:

即解锁角度β需大于8.5°。
1.3.3 锥面角度SCMRT锁紧后,锁块受到锁紧滑块的约束而无法解锁,锁紧滑块外表面与锁块的内表面相接触,接触面设置为锥面,该锥面与轴向方向的夹角为锥面角度。
不同于锁块的锁紧角度和解锁角度是为了避免产生自锁效应,锁紧滑块上的锥面角度却是要产生自锁,利用自锁原理来实现锁紧滑块对锁块的约束。锁紧锥面受力分析图如图 3所示。

|
| 图 3 锁紧锥面受力分析 Fig. 3 Forces on the locking cone |
图 3中:γ为锁紧时锁块与锁紧滑块外壁贴合面与轴向方向的夹角;F3为锁块受到SCM的作用力;F3x为由F3分解得到的沿水平方向锁块对锁紧滑块的推力;F3y为由F3分解得到的沿轴向向下的力;F3xt为由F3x分解得到的沿锥面方向的力;F3xn为由F3x分解得到的锁块对锁紧滑块锥面的正压力。
要实现自锁,需满足以下条件:

整理得:

摩擦因数μ1取最小值0.1,计算得到:
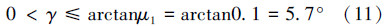
此时,只要锁紧滑块的约束存在,无论解锁力多大,锁块都不会自动解锁。但锥面角度过小会导致SCM锁紧机构锁紧不到位或锁块磨损[7]。
2 锁紧机构有限元分析 2.1 材料选用SCMRT锁紧单元主要由ROV驱动杆、锁紧连杆、锁块、锁紧外壳和锁紧滑块等组成。分析时取主要的受力部件进行分析,即锁块、锁紧滑块、锁紧壳体以及SCM。各部件材料性能如表 1所示。
| 部件 | 材料 | 弹性模量/GPa | 泊松比 | 屈服强度/MPa | 抗拉强度/MPa | 密度/(kg·m-3) |
| 下部壳体 | 8630 | 210 | 0.3 | 372 | 564 | 7 800 |
| SCM | 4340 | 210 | 0.3 | 835 | 980 | 7 850 |
| 锁块 | 8630 | 210 | 0.3 | 372 | 564 | 7 850 |
| 锁紧滑块 | 8630 | 210 | 0.3 | 372 | 564 | 7 850 |
SCM安装工具计算工况有3种:锁紧工况、提升工况和冲击工况,在这3种工况下计算模型、载荷条件、边界条件及计算方法都不同。笔者只针对锁紧工况进行分析。
锁紧工况下的载荷条件为:SCMRT在锁紧工况中,锁紧壳体和SCM是固定的,在锁紧连杆推力下锁紧滑块沿轴向下移0.04 m并挤压锁块,锁块沿径向运动锁紧到SCM锁紧槽内,即只允许锁紧滑块竖直方向的位移,限制锁块在竖直方向的位移。
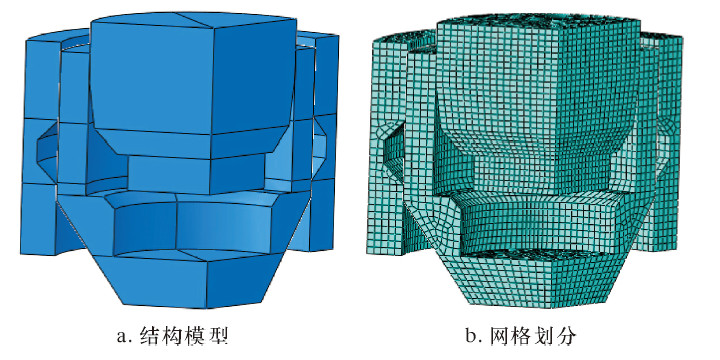
在锁紧工况中,由于锁紧机构中有3个锁块,为了方便计算,在ABAQUS中只需取其中1个,即模型的 1/3 进行分析。考虑模型各接触面的情况,定义摩擦因数为0.15。结构模型及网格划分如图 4所示。
|
| 图 4 锁紧机构结构模型及网格划分 Fig. 4 The structure model of locking mechanism and mesh generation |
锁紧单元的应力云图如图 5所示。由图可以看出,应力变化主要发生在锁块下部与锁紧外壳台阶接触的地方,应力存在集中,此处也是最大应力存在的地方,最大应力值为201.9 MPa,小于材料的许用应力248.0 MPa,满足设计的强度要求,可以实现锁紧。

|
| 图 5 锁紧机构应力云图 Fig. 5 Mises stress distribution of the locking mechanism |
在ABAQUS后处理模块中,提取出最大Mises应力随时间变化的曲线,如图 6所示。其中横坐标为锁紧过程时间点,此处设置2个分析步,每个分析步的时间为1 s。从图 6可以看出,当接触发生后,应力在后端发生突然增大。这是因为此时锁紧滑块下端斜面与锁块下端斜面刚发生接触,应力变化较大,当锁紧滑块向下移动到位时,锁块则被锁紧到SCM锁紧槽内。

|
| 图 6 最大应力处应力随时间变化曲线 Fig. 6 The maximum stress over time |
图 7为不同角度时应力随时间变化的曲线。图中红色曲线代表锥面角度大于5.7°、锁紧/解锁角度大于8.5°;黑色曲线代表锥面角度小于等于5.7°、锁紧/解锁角度大于8.5°;绿色曲线代表锁紧/解锁角度小于8.5°、锥面角度小于等于5.7°。从图中可以看出,当锥面角度大于5.7°,应力在分析步2时达到屈服强度372 MPa,锁块此时出现屈服。当锁紧/解锁角度小于8.5°,应力在50 MPa,此时无论锁紧滑块向下的推力有多大,锁块都无法向锁槽内滑动,即锁紧面发生自锁,这与理论分析结果一致。

|
| 图 7 锁紧/解锁角度和锥面角度随时间的应力变化曲线 Fig. 7 The locking / unlocking angle and cone angle over time |
(1)锁块锁紧角度α只要大于8.5°就不会发生自锁;解锁角度β需大于8.5°;锥面角度γ大于5.7°锁块就不会自动解锁。
(2)建立了SCMRT锁紧工况模型,分析得出最大Mises应力发生在锁块下部与锁紧外壳台阶接触的地方,所建立的有限元模型分析结果可靠。
| [1] | 张鹏举,梁斌,刘康,等.水下控制模块总体设计的研究[J].机电产品开发与创新,2014,27(6):113-115. |
| [2] | 张丰功,王定亚,李磊,等.水下控制模块的技术分析与发展建议[J].石油机械,2013,41(6):59-62. |
| [3] | 朱高磊,赵宏林,段梦兰,等.水下采油树控制模块设计要素分析[J].石油矿场机械,2014,42(10):1-6. |
| [4] | Vick J D,Mille J W.A wireline-retrievable wellhead plug system for use with horizontal trees[R].OTC 7917,1995. |
| [5] | 王焕定,王伟.有限单元法教程[M].哈尔滨:哈尔滨工业大学出版社,2003:45-50. |
| [6] | 成大先.机械设计手册[M].北京:化学工业出版社,2004:8-10. |
| [7] | Vick J,Robb E,Thomson D.A static slickline-retrieva ble wellhead plug system for use with horizontal trees in offshore systems[R].SPE50591,1998. |



