0 引 言
提高钻进效率是降低油气井钻井成本最有效的途径,水射流辅助破岩被认为在提高钻速、防止漏失和提高钻井系统可靠性等方面效果显著[1]。为了提高射流在井底的作用效率,钻井研究者们相继设计并开发了加长喷嘴、空化喷嘴和自激振荡喷嘴等[2],研究结果证明,水力脉冲射流比连续射流有更大的瞬时速度和冲击压力[3]。
脉冲射流在井底能够产生瞬时负压和脉冲冲击等作用[4],减小岩屑的压持效应,提高破岩和清岩效率。目前,水力脉冲射流研究主要集中在脉冲射流的瞬时速度和冲击压力等方面,以及水力脉冲射流对岩石破碎[5]或表面清洗的作用效果,缺乏水力脉冲射流压力波动特性的研究。然而,脉冲射流波动特性及其作用范围对于井底压力预测与控制,保持井壁稳定等有着重要影响。笔者拟研究水力脉冲射流压力波动随管路变化的趋势,通过数值模拟分析管路长度和粗糙度等因素对脉冲压力波动特性的影响,并通过室内试验进行验证。
1 水力脉冲射流特性计算模型建立水力脉冲射流发生器主要由本体、弹性挡圈、导流体、叶轮总成和自激振荡腔室等组成[6],钻井作业时,水力脉冲射流发生器安装在钻头上部,将流体的扰动作用和自振空化效应耦合,将进入钻头的常规连续流动调制成振动脉冲流动,在钻头喷嘴出口形成脉冲空化射流,产生3种效应[7, 8, 9]: ① 水力脉冲。改善井底流场,提高井底净化和清岩效率,减少压持和重复破碎。② 空化冲蚀。辅助破岩,提高破岩效率。③ 瞬时负压。井底瞬时负压脉冲,局部瞬时欠平衡。
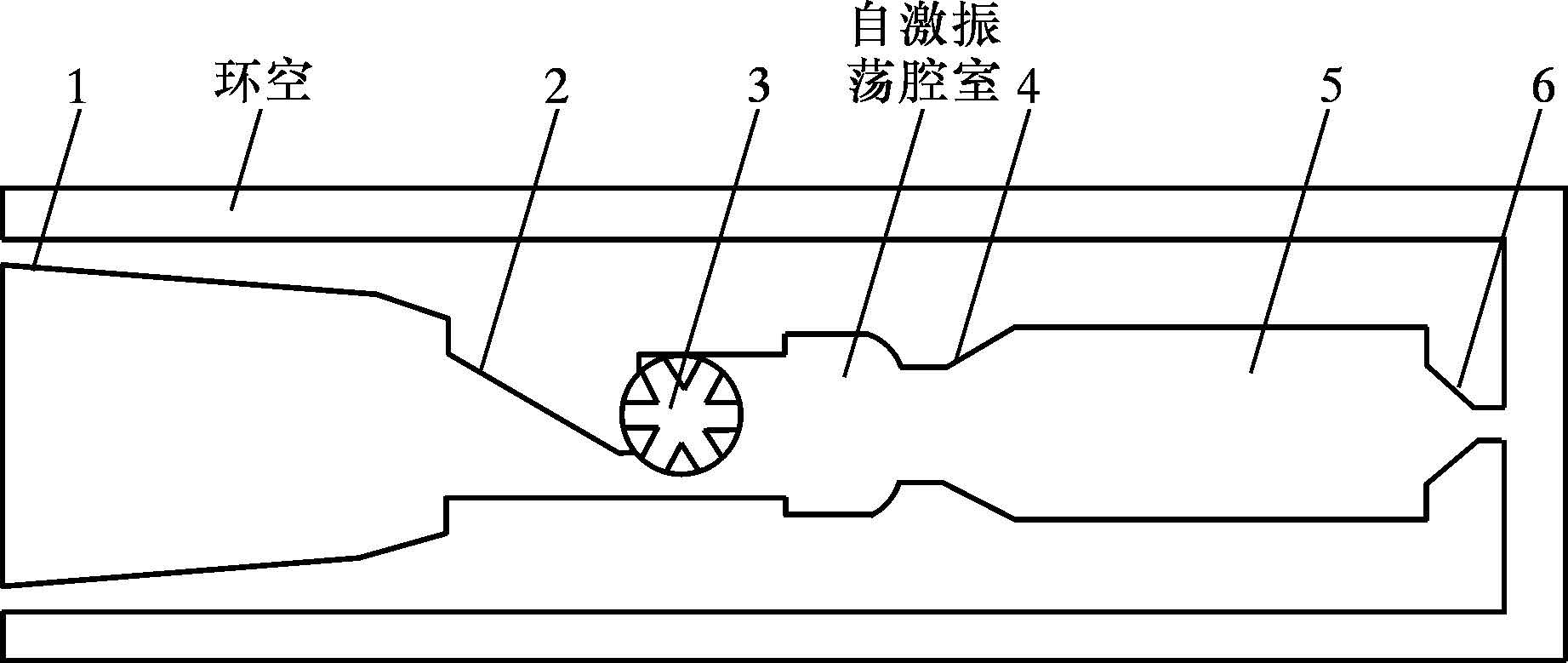
1.1 求解域网格划分及边界条件为开展水力脉冲射流压力波动特性数值研究,水力脉冲射流发生器需将连续流体流动调制为脉冲射流,以确定起始脉动压力幅值、波动周期等初始条件。射流发生器的流场区域从上内接头入口开始,经导流体、叶轮、自激振荡腔室及喷嘴、下内接头和等效钻头喷嘴等,最终到环空出口处。由于水力脉冲射流发生器的结构近似为平面对称结构,故采用二维数值模拟方案。流体从左端上内接头进入,先后流经导流体、叶轮、自激振荡腔室及喷嘴和下内接头等部件,再由等效钻头喷嘴喷出后进入环空。利用Gambit软件对计算域采用结构化网格模型进行划分[10],并在叶轮旋转区域进行局部网格加密,以提高计算精度。所建的水力脉冲射流发生器物理模型如图 1所示。
|
| 1—上内接头;2—导流体;3—叶轮;4—自激振荡喷嘴;5—下内接头;6—等效钻头喷嘴。 图 1 水力脉冲射流发生器物理模型 Fig.1 Physical model of hydraulic pulsed jet generator |
边界条件:入口为速度(排量)边界条件;出口为自由出流边界条件。利用滑动网格法模拟叶轮的流场,叶轮表面采用速度无滑移条件,脉冲发生器的外壁为固定壁面,叶轮为旋转壁面[11]。
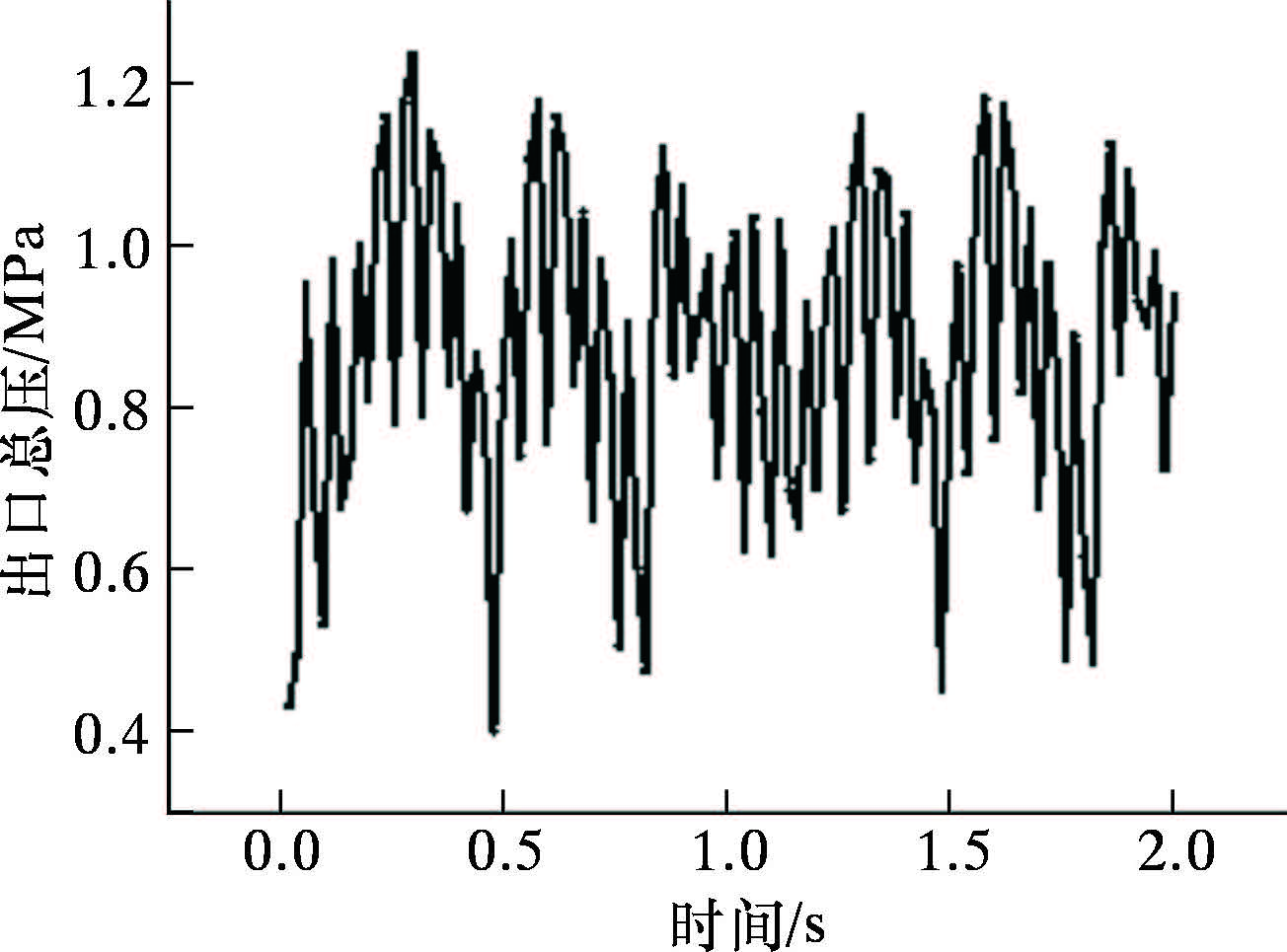
1.2 水力脉冲射流压力波动特性初始条件在Fluent软件中预先设定叶轮的旋转速度,由于入口排量和叶轮转速存在一定关系,这里设定入口排量10 L/s,旋转速度180 r/min,监测发生器振荡喷嘴出口处的压力波动情况,结果如图 2所示。
|
| 图 2 振荡喷嘴出口总压随时间变化的规律 Fig.2 Total pressures at self-oscillation nozzle outlet over time |
6叶片叶轮脉冲工具的振荡喷嘴出口处出现明显压力波动,从图 2可以看出,波动幅度为0.5~0.8 MPa,6个叶片周期性对来流施加扰动,叶轮每旋转 1/6 圈为1个波动周期。出口的压力波动频率与叶轮转速相关,叶轮每转动1圈,出口压力波动发生6个周期性变化。
为了探究稳定周期性脉动压力在后接管路中的波动特性,主要分析管路长度和粗糙度对出口压力波动的影响规律。根据压力脉动的数值模拟结果可以看出,波动周期T=0.055 s,即频率f=18 Hz,压力最小值约为0.4 MPa,压力最大值约为1.2 MPa。因此,可在Fluent中编译UDF函数来模拟叶轮脉冲工具产生的脉动压力,设定管路入口压力随时间发生周期变化,入口压力满足关系式p=0.4sin(114t)+0.8,时间单位为s。通过改变管路长度和粗糙度等参数,分别在距入口不同距离处测量总压、脉动压力幅值和速度等参数,分析不同参数的影响规律。
2 数值模拟计算模拟水力脉冲发生器在入口排量10 L/s时的工作情况,在Fluent中设定管路入口压力满足p=0.4sin(114t)+0.8的正弦变化,出口压力为0 MPa,长度为19 m,粗糙度为0.04 mm,监测距离管路入口1、3、5、7和9 m截面处的压力波动情况,模拟结果如图 3所示。

|
| 图 3 距入口不同位置处总压随时间变化的规律 Fig.3 Total pressures at different positions from inlet over time |
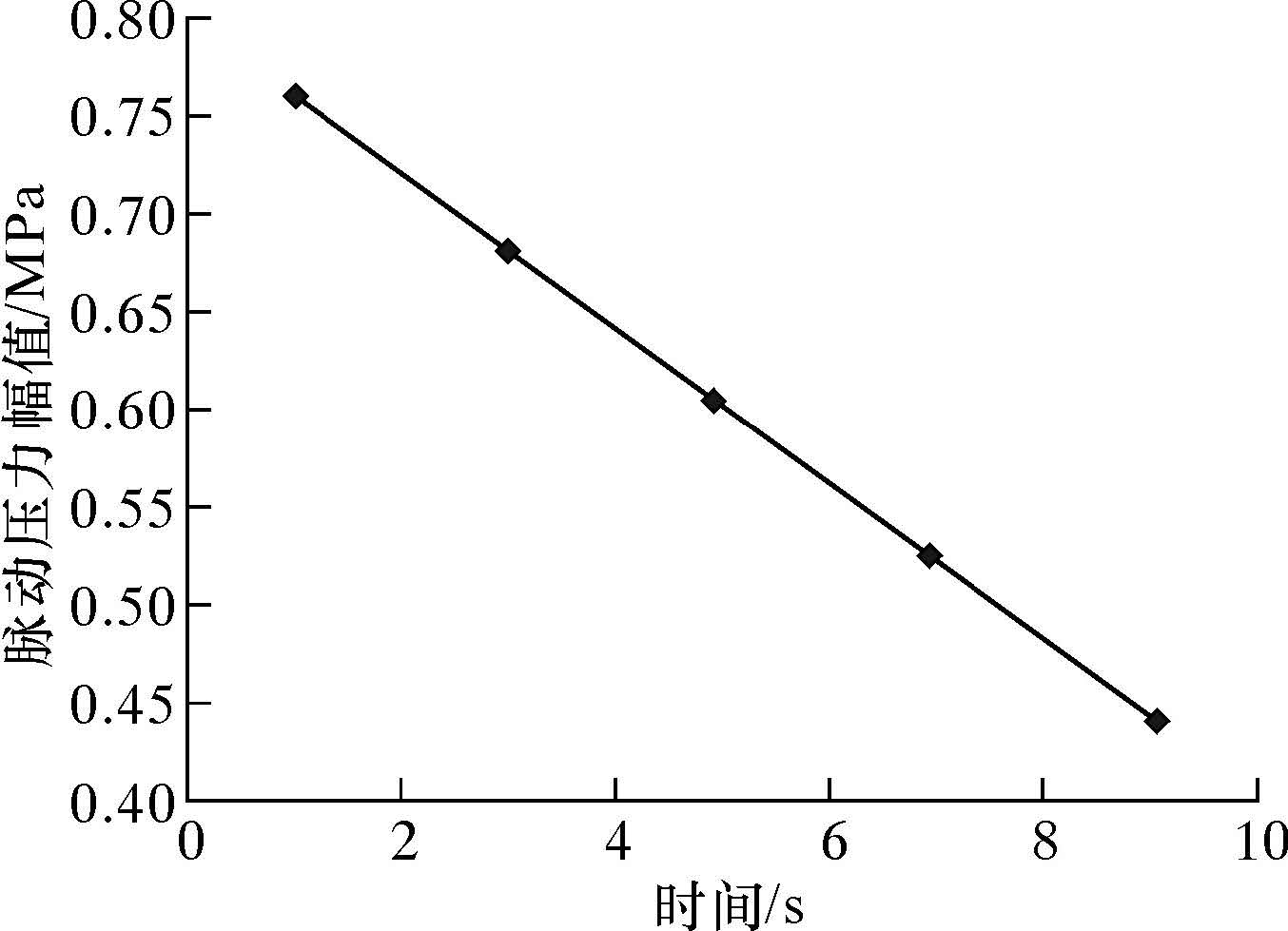
稳定后的压力脉动幅值在1、3、5、7和9 m处分别为0.76、0.68、0.60、0.52和0.44 MPa,即在管路长度和相对粗糙度一定的条件下,脉动压力幅值随流体距入口距离的增大呈线性衰减,如图 4所示。在该条件下,脉动压力幅值随流体在管路内流动的变化关系式为:Δp=Δpini+cd1,Δpini=0.80 MPa,c=-0.04 MPa/m。其中,Δp=pmax-pmin,MPa;d1为测点距压力入口的距离,m。
|
| 图 4 脉动压力幅值随流体距入口距离变化的规律 Fig.4 The effect of fluid distance from inlet on the pressure fluctuation amplitude |
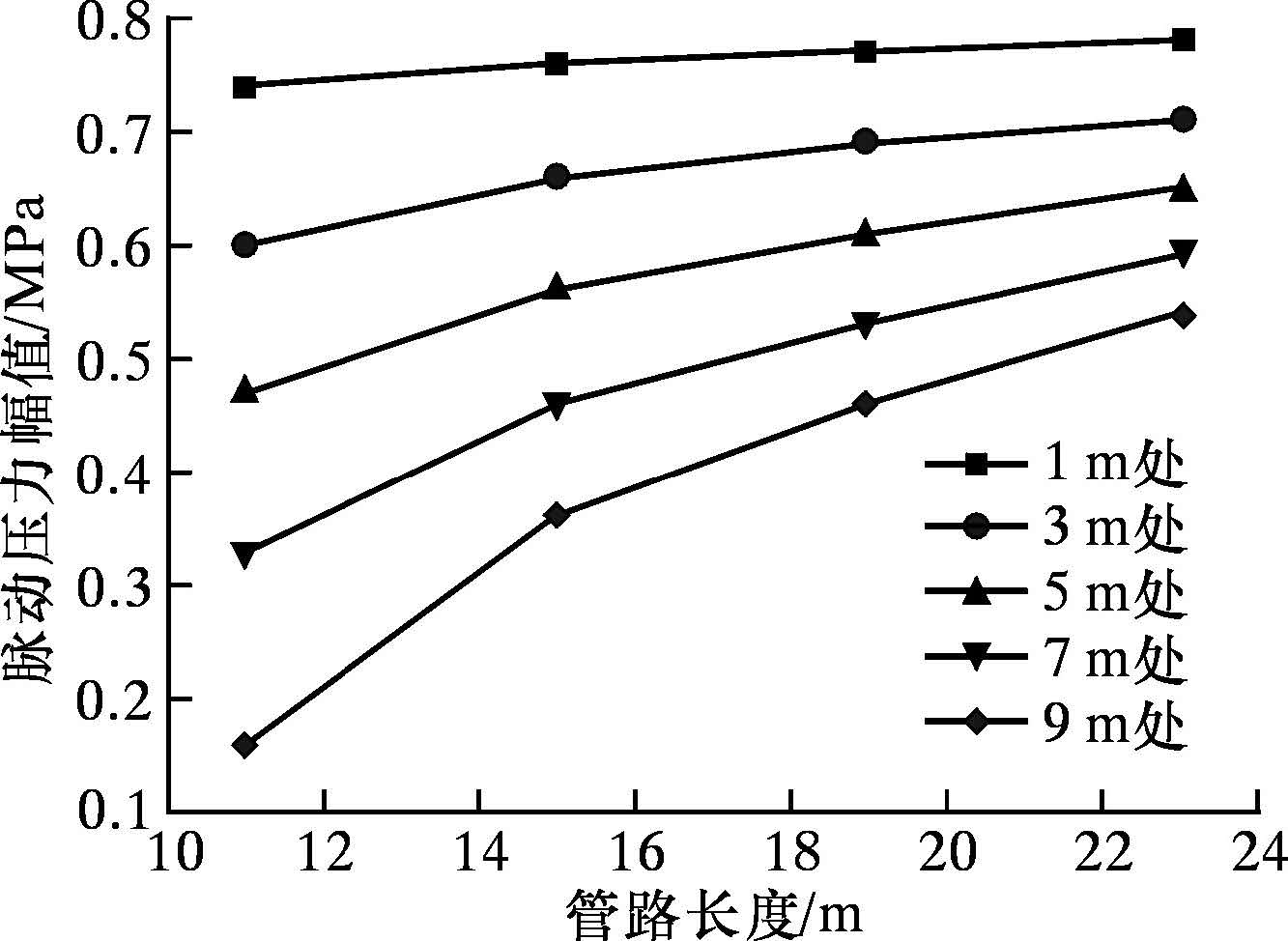
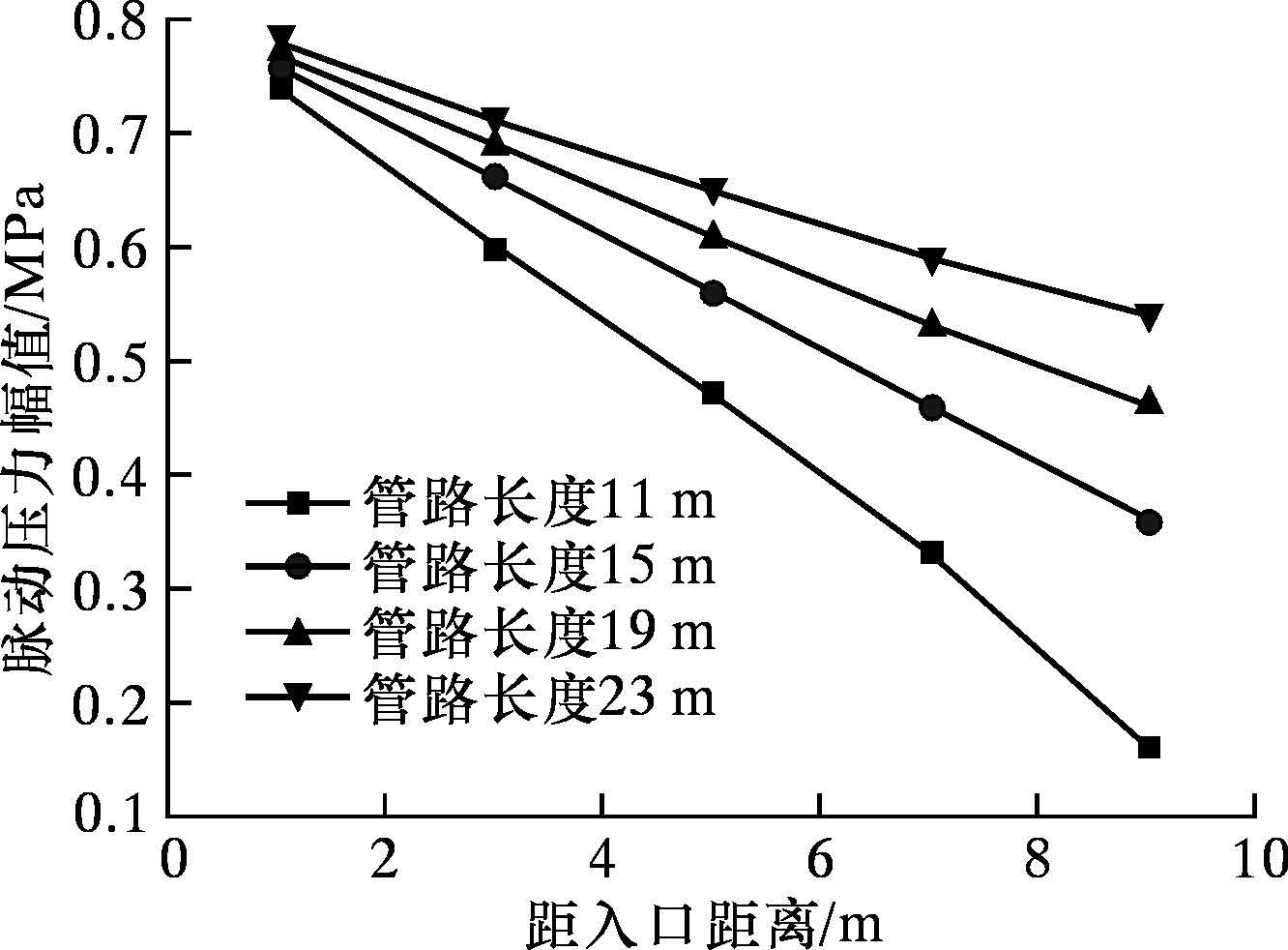
在管路进、出口压力一定的情况下,管路长度是影响压力脉动幅值的主要因素之一。入口压力满足p=0.4sin(114t)+0.8,出口压力为0 MPa,设定管路长度分别为11、15、19和23 m,测定管路不同位置截面处(1、3、5、7和9 m)的压力脉动变化规律。图 5表示相同压力入口的脉冲射流在管路中距入口1、3、5、7和9 m处的脉动压力幅值随管路长度变化关系曲线。由图可知,随着管路长度的增加(11~23 m),相同位置处脉动压力幅值逐渐增大。
|
| 图 5 脉动压力幅值随管路长度变化曲线 Fig.5 The effect of hose length on the pressure fluctuation amplitude |
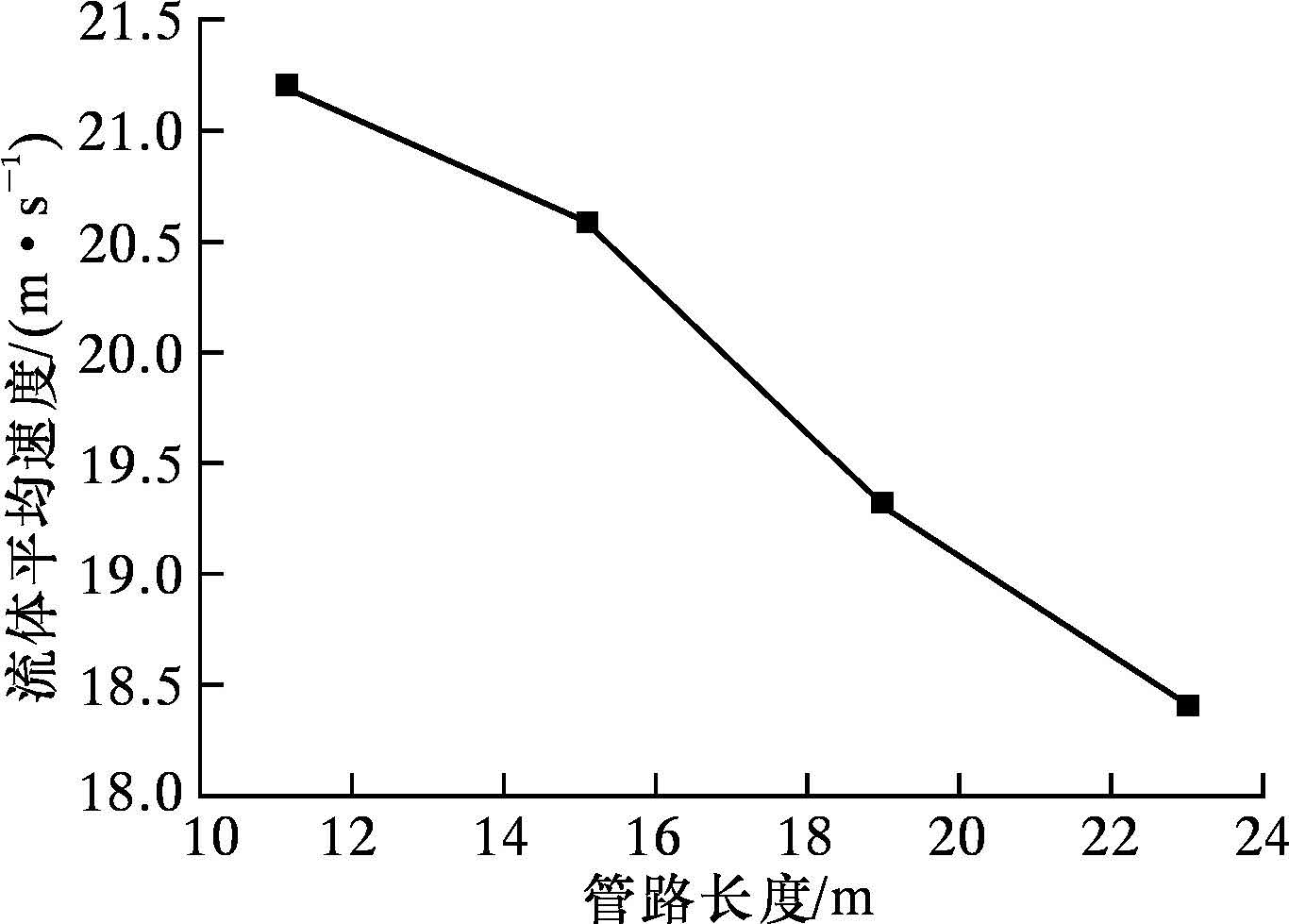
液体的流动状态可以用雷诺数来判断,所有管路中的雷诺数均满足Re=vd/μ,Re∈(2 100,100 000),故流体流动为非定常湍流。流体平均流速无法通过显式方程得到,可采用数值模拟方法得到不同长度圆管中流体平均流速,如图 6所示。由图可知,管路越长,流体平均速度v越小。
|
| 图 6 流体平均速度随管路长度变化的趋势 Fig.6 The effect of hose length on the average fluid velocity |
取不同长度的2根水平管,长度分别为L1和L2(L1<L2),且相对粗糙度ε/d=0,压力入口与压力出口设定同上,则2管中平均流速满足v1—>v2—,Re在2 100~100 000之间。下面分析距2管入口l处的压力情况。根据Blassius公式绘制的简单诺模图和管道水力光滑摩阻曲线,将Fanning公式变形后可得圆管中紊流的摩阻损失公式(工程单位)为[12]:
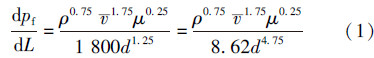
式中:ρ表示流体密度,d表示圆管直径,μ表示动力黏度。
因此,1、2管中距离流体入口l处的压力损失可表示为:
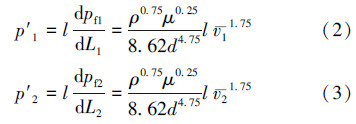
由于v1>v2,故p′1>p′2,即相同位置处,1管压力损失大于2管压力损失,流体遇到的流动阻力增大,脉动压力下降幅度增大,脉动压力衰减值增大。由此可以证明,相同位置处脉动压力幅值随着管路长度的增加而增大。
此外,随着流体在管路中前进,脉动压力幅值呈线性衰减。管路越长,脉动压力幅值衰减越慢,即脉动压力幅值的衰减随管路长度的增加而逐渐减小,如图 7所示。11~23 m 4种不同长度圆管中,脉动压力幅值随流体在管路内流动的变化关系式均满足Δp=Δpini+cid1,其中Δpini=0.80 MPa,ci中i=1、2、3、4,分别对应管路长段为11、15、19和23 m,取值分别为-0.07、-0.05、-0.04和-0.03 MPa/m。
|
| 图 7 不同长度管路脉动压力幅值随距离变化的规律 Fig.7 The effect of distance from inlet on the pressure fluctuation amplitude under different hose length |
出现上述规律是因为脉动压力幅值的衰减主要由流体在管路中的压力损失决定,即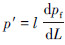 =
=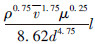 。由此可以看出,在流体平均速度一定的情况下,p′∝l,即脉动压力幅值衰减随测点到压力入口距离l的增加而线性变化。而管路越长,流体平均流速越小,单位长度压力损失越小,所以脉动压力幅值衰减越慢。
。由此可以看出,在流体平均速度一定的情况下,p′∝l,即脉动压力幅值衰减随测点到压力入口距离l的增加而线性变化。而管路越长,流体平均流速越小,单位长度压力损失越小,所以脉动压力幅值衰减越慢。
管壁粗糙度对流动阻力的影响主要是由于流体在管道中流动时,流体质点与管壁凸出部分相碰撞而增加了流体的能量损失。本节将模拟长度为19 m的圆管中不同粗糙度对脉动压力幅值的影响规律。如图 8所示,在管路长度一定、相对粗糙度在0~4.211×10-3范围内,不同粗糙度圆管内相同位置处的脉动压力幅值基本一致,且随着流体在各个管路中前进,脉动压力幅值呈线性衰减。
|
| 图 8 各测点脉动压力幅值随管路粗糙度变化的规律 Fig.8 The effect of hose roughness on the pressure fluctuation amplitude at different measure points |
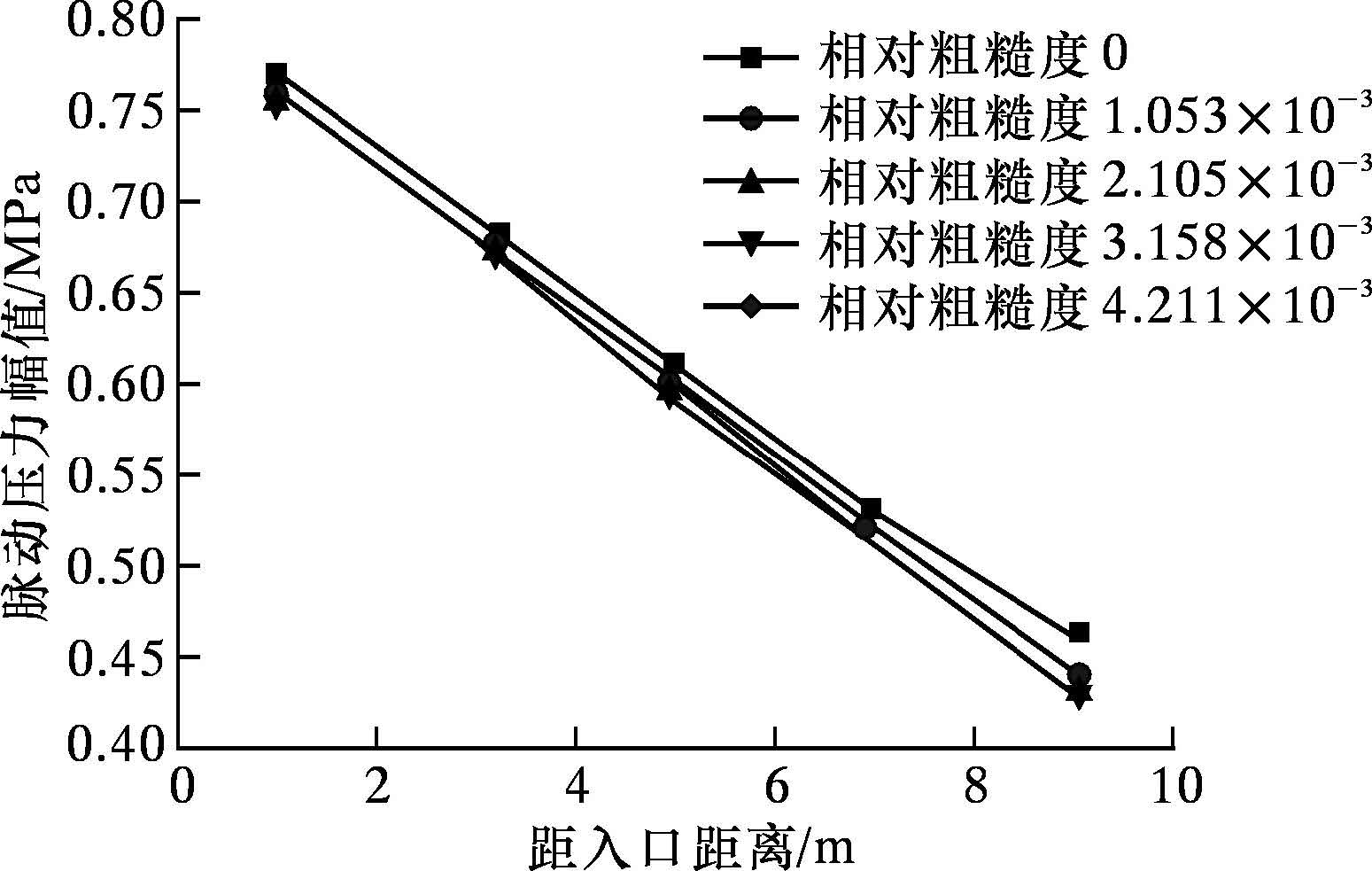
由于粗糙度不为0,故不能采用公式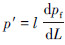 来计算压力损失,可用Moody摩擦因数图计算管内压力损失[13]。下面分别以粗糙度0.08和0.12 mm圆管、距离入口5 m处的压力波动情况进行示例,其他情况处理方法相同。
来计算压力损失,可用Moody摩擦因数图计算管内压力损失[13]。下面分别以粗糙度0.08和0.12 mm圆管、距离入口5 m处的压力波动情况进行示例,其他情况处理方法相同。
粗糙度为0.08 mm时,数值模拟得出19 m长的圆管内平均速度v=13.3 m/s,雷诺数为:
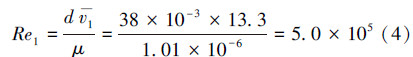
流动为湍流。相对粗糙度ε1/d=0.000 08/0.038=2.105×10-3,根据Re和相对粗糙度,查Moody图得到λ1=0.024。因此距离入口5 m处的能量损失为:
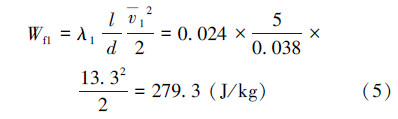
压力损失为:
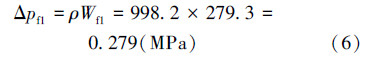
粗糙度为0.12 mm时,19 m长的圆管内平均速度v2=12.5 m/s,采用相同的处理方法可以得到:
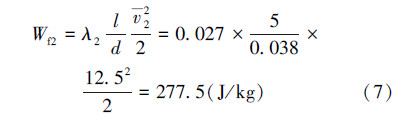
压力损失为:
由计算结果可以得出,不同粗糙度圆管相同位置处压力损失基本相同,因此脉动压力下降幅度基本相同,脉动压力衰减值也类似。此外,在各管中平均速度一定的条件下,能量损失与l成线性正相关,脉动压力幅值呈线性衰减。
3 室内试验为了进一步分析水力脉冲射流发生器的脉动特性,笔者通过室内试验研究了不同排量对水力脉冲射流压力波动幅值的影响。
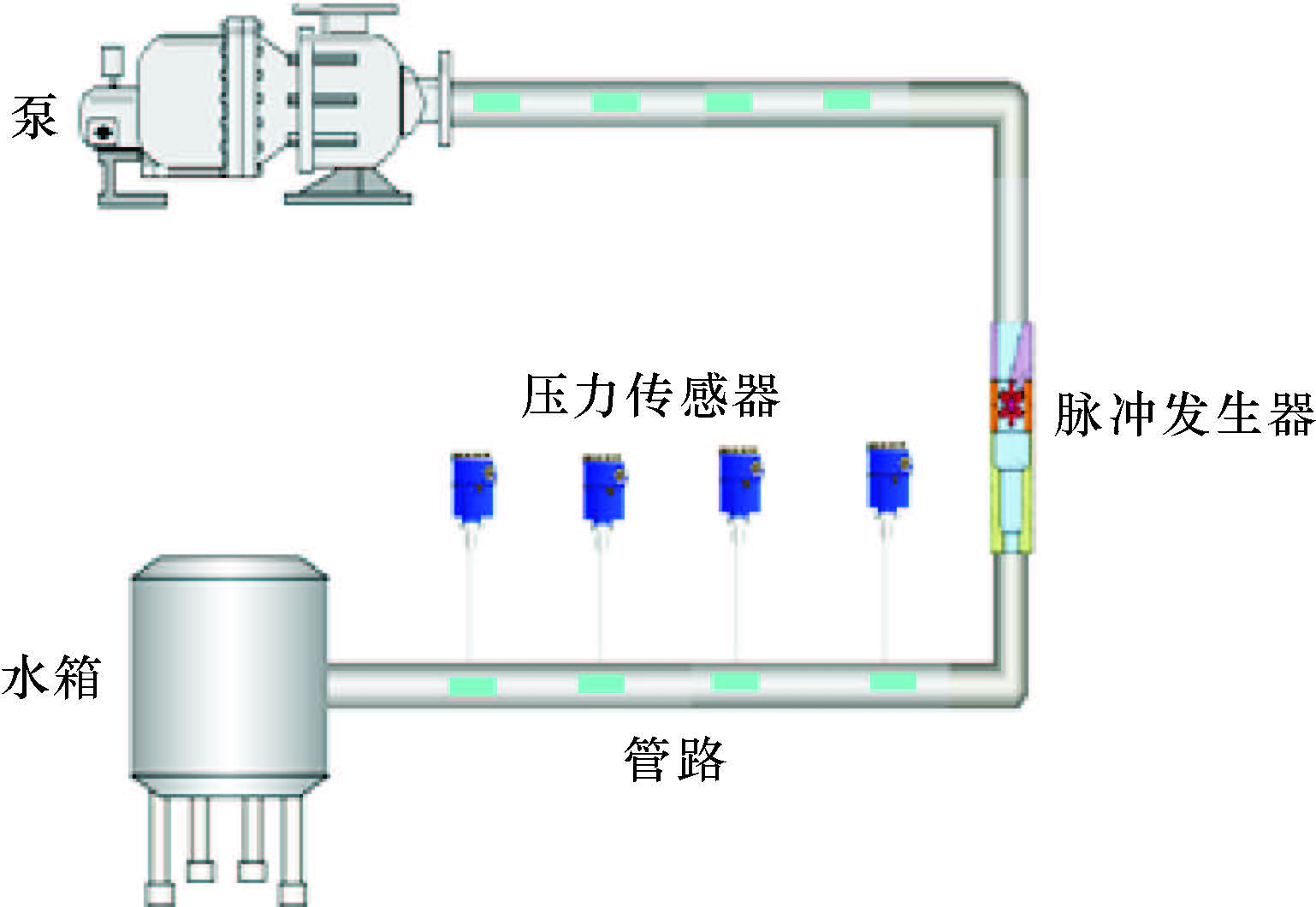
3.1 试验设备水力脉冲射流压力波动特性室内试验在中国石油大学(北京)高压水射流与完井实验室进行。试验设备主要有:①橇装式三缸柱塞高压泵1台,最高可实现压力70 MPa,最大排量650 L/min,柴油机功率383 kW;②127 mm叶轮式水力脉冲射流发生器1个;③高压胶管,总长度20 m,内径38 mm,最大承压30 MPa;④压力传感器6个,传感器量程30 MPa,输出电流4~20 mA;⑤数据采集系统,美国NI公司生产的PCI-6259数据采集卡及配套的数据采集系统。
3.2 试验方案试验装置连接如图 9所示。试验介质为水,连接叶轮式水力脉冲射流发生器和高压胶管,高压流体被泵入水力脉冲射流发生器,经谐振腔喷嘴产生脉冲射流后流入高压胶管。在脉冲射流发生器出口以及高压胶管中距离发生器出口1、3、5、7及9 m处安装压力传感器,可通过数据采集系统监测各测点的压力变化,得到水力脉冲射流压力波动幅值在后接管路中的衰减规律。
|
| 图 9 水力脉冲射流压力波动特性试验装置连接图 Fig.9 Connection of experimental apparatus for hydraulic pulsed jet pressure fluctuation characteristic test |
采样时间分别取0.05、0.02和0.01 s,在泵排量10 L/s的试验条件下进行初步试验。结果显示在采样时间0.02和0.01 s 时,相同时间间隔内出现的脉动周期已经一致,因此采样时间取0.02 s。试验过程中,通过调节柱塞高压泵挡位,在安全压力范围内测试5组流量(6、7、8、9和10 L/s)条件下各测点的压力变化。
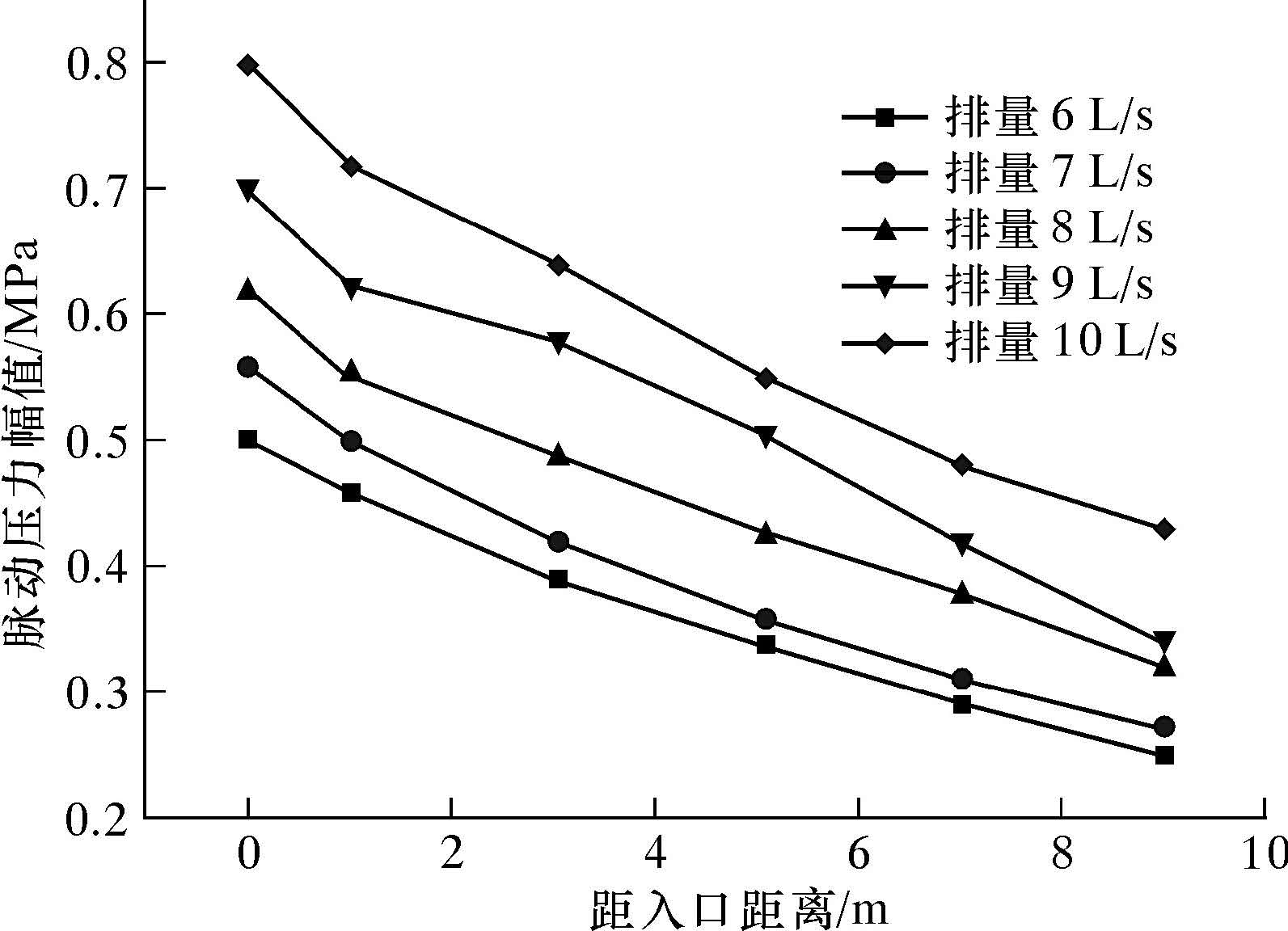
3.3 试验结果通过室内试验,得到不同排量下各测点脉动压力幅值变化规律,如图 10所示。由图可以看出,在不同排量下,脉动压力幅值均随测点距脉冲工具出口距离增加而呈近似线性衰减,从而验证了上节数值模拟结果的正确性,且排量越大,相同测点的脉动压力幅值越大。
|
| 图 10 不同测点脉动压力幅值随排量变化的规律 Fig.10 The effect of displacement on the pressure fluctuation amplitude at different measure points |
这是因为水力脉冲射流发生器的出口压力是由入口压力减去压耗得出的,随着入口流量的增大,入口压力也随之增大,同时由于入口速度的增大,叶轮的摩擦阻力增大,从而使水力脉冲射流发生器的摩阻增大,但摩阻及压降的增大幅度远小于发生器入口压力的增大幅度,所以出口压力幅值随着入口流量的增大而增大,后接管路中相同测点的脉动压力幅值也随之增大。
4 结 论(1)水力脉冲射流发生器能将连续射流调制成脉冲射流,并在后接管路中形成周期性压力波动。在管路入口相同起始波动压力和相同出口压力条件下,管路越长,管内相同位置处脉动压力幅值越大。
(2)随着流体在管路中前进,脉动压力幅值呈线性衰减,且脉动压力幅值的衰减随管路长度的增加而逐渐减小。
(3)在管路长度、入口及出口压力条件相同的情况下,管路相对粗糙度在0~4.211×10-3范围内,不同粗糙度圆管内脉动压力幅值基本一致。
(4)在后接管路长度和粗糙度一定的条件下,管路中的脉动压力幅值随水力脉冲射流发生器入口排量的增大而呈增大趋势。
| [1] | Cohen J H,Deskins G.High-pressure jet kerf drilling shows significant potential to increase ROP[R]. SPE96557,2005. |
| [2] | Fu J,Li G,Shi H,et al.A novel tool to improve the rate of penetration hydraulic pulsed cavitating-jet generator[J].SPE Drilling and Completion,2012,27(3):354-361. |
| [3] | Liu Shuang,Li Gensheng.Application of hydraulic pul-sed jet generator for ROP enhancement in shale gas well[C]//12th Offshore Mediterranean Conference and Exhibition.Italy,March 25-27,2015. |
| [4] | 史怀忠,李根生,沈忠厚,等.水力脉冲空化射流发生器配合Power V防斜打快技术[J].石油机械,2009,37(1):14-17. |
| [5] | Wei Minghui,Li Gensheng.Theories and applications of pulsed-jet drilling with mechanical specific energy[R].SPE174550-PA,2015. |
| [6] | 李根生,史怀忠,沈忠厚,等.水力脉冲空化射流钻井机理与试验[J].石油勘探与开发,2008,35(2):239-243. |
| [7] | 王智锋.负压脉冲钻井技术理论及方法[J].石油钻采工艺,2005,27(6):13-15. |
| [8] | 李根生,沈忠厚,张召平,等.自振空化射流钻头喷嘴研制及现场试验[J].石油机械,2003,31(5):11-12. |
| [9] | 李根生,沈忠厚,周长山,等.自振空化射流研究与应用进展[J].中国工程科学,2005,7(1):27-32. |
| [10] | 朱红钧,林元华,谢龙汉.Fluent12流体分析及工程仿真[M].北京:清华大学出版社,2011. |
| [11] | 余华兵,康士廷,胡仁喜,等.Fluent14.5流场分析从入门到精通[M].北京:机械工业出版社,2014. |
| [12] | 吴望一.流体力学[M].北京:北京大学出版社,1983. |
| [13] | 汪志明,崔海清,何光渝.流体力学[M].北京:石油工业出版社,2006. |




