2. 中国石油大学(北京)地球物理与信息工程学院
2. College of Geophysics and Information Engineering, China University of Petroleum(Beijing)
0 引 言
声波测井仪上,隔声体位于接收器和发射器之间,是声波测井仪器的关键部件之一。隔声体的主要功能是隔离纵向和横向的振动,有效地衰减和延迟有害的直达声波干扰[1, 2]。隔声体的性能直接影响声波测井仪器的性能,因此研究出隔声性能好的隔声体对研发现代测井仪器具有重大意义。
国外对声波测井仪的理论研究经历了如下几个阶段。1952年,Biot孔隙介质理论提出;20世纪70年代末,声波测井理论发展起来;从几何声学到理论声学(波动理论),通过数学分析、数值模拟和试验测量使声波测井理论得到完善。近几年,北京航空航天大学和中石化胜利石油工程有限公司钻井工艺研究院等单位已开始着手进行测井仪隔声体方面的理论研究和生产应用,并已卓有成效。2007年,中国石油集团测井有限公司研制出了多极子阵列声波测井仪MPAL[3]。
笔者对声波测井仪的外壳声传播特性建模计算方法进行了研究。首先研究无隔声槽圆筒的声传播特性和建模计算方法,并与理论值进行对比,以检验建模计算方法的正确性;再对有隔声槽圆筒(声波测井仪的外壳)进行隔声特性分析,并将计算结果与无隔声槽的圆筒的结果进行对比。结果表明,笔者的建模计算方法正确,且有隔声槽的圆筒性能优于无隔声槽的圆筒,满足测井要求。
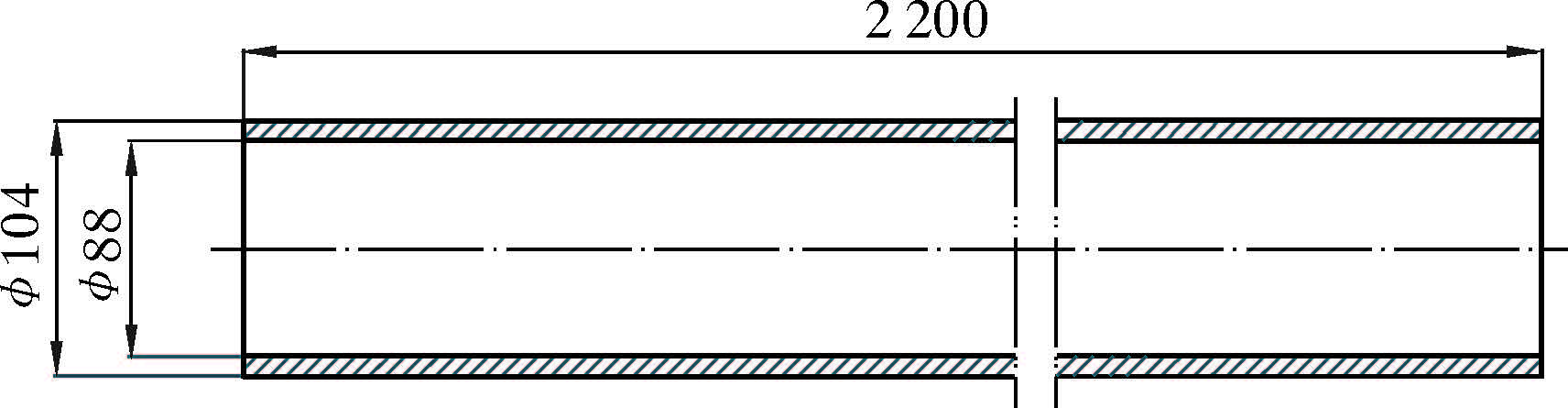
1 无槽圆筒隔声性能分析 1.1 无槽圆筒计算条件无隔声槽的声波测井仪外壳:外径104 mm,壁厚8 mm,长2.2 m(见图 1)。声波从下端(右端)传到上端(左端)。计算声波传递过程中的衰减系数和传递时间。
|
| 图 1 无槽隔声体结构图 Fig.1 Structure schematic of acoustic insulator without groove |
圆筒材料:17-4PH,属于马氏体沉淀硬化型不锈钢,易于调整强度级别。密度7 500 kg/m3,弹性模量202 GPa,泊松比0.3。
声源:频率f=14 kHz的雷克子波(Ricker)。它是由标准高斯函数的二阶导数取反而来,只在脉冲峰附近很短的一段时间内有能量分布。
声源加载在主应力节点上,声源为雷克子波(Ricker wavelet)函数,表达式为:
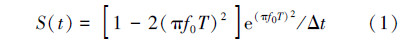
其中
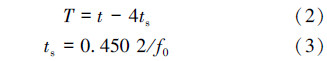
式中:ts是时移参数,f0为声源中心频率,Δt为时间步长。
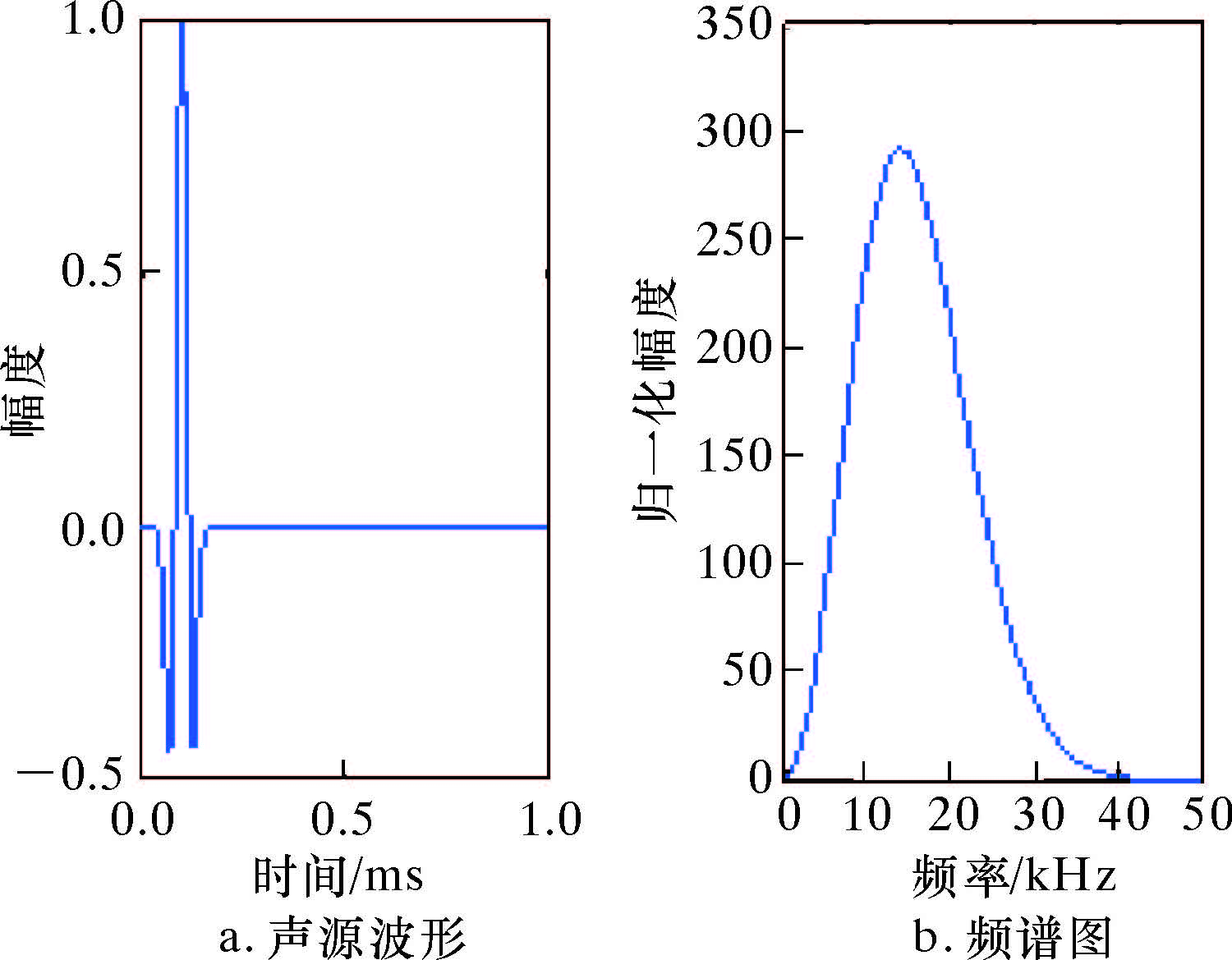
声源中心频率f0=14 kHz时的声源波形及其频谱图如图 2所示。
|
| 图 2 中心频率为14 kHz的声源波形及其频谱图 Fig.2 The waveform and spectrum of sound source with the center frequency of 14 kHz |
声波的传递也是一种振动,因此可以利用ANSYS软件将声波的振动转化为振动载荷施加在波测井仪外壳的一端,通过对声波传递过程的分析,得到声波传递到外壳另一端的衰减和延迟状况。
在测量隔声体的性能时,应在隔声体的两端各连接一定长度的补偿管用于模拟隔声体上、下两端的部件和消除边缘效应[4]。因此,希望得到一个不受反射波干扰的首波,须将隔声体的两端加长。
雷克子波的周期约为7.143×10-5 s,需要的距离为0.43 m,因此,在隔声体的两端至少加长L/2,约为0.215 m。
1.2 无槽隔声体建模数值模拟时采用主频14 kHz的宽带Ricker子波声源函数,见式(1)。
在三维建模软件Solidworks中建立无槽隔声体的三维结构图。将三维模型导入到ANSYS中,采用Solid 185号单元划分网格。Solid 185号单元用于构造三维固体结构单元,通过8个节点来定义,每个节点有3个沿着X、Y、Z方向平移的自由度,单元具有超弹性、应力钢化、蠕变、大变形和大应变能力[5]。通过ANSYS软件设定材料的弹性模量值、泊松比和密度值。
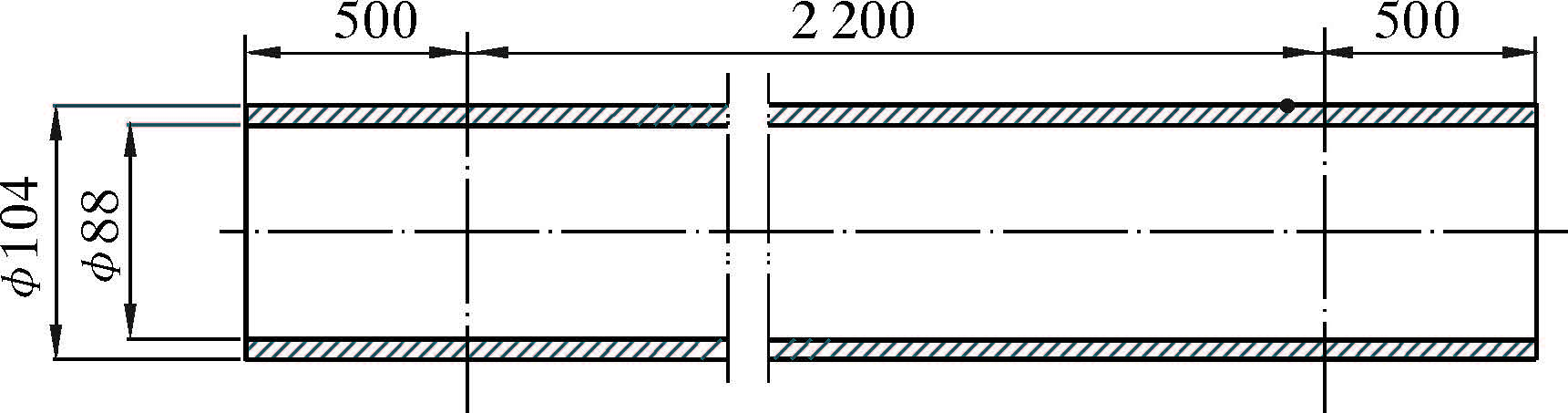
设定好参数后进行网格划分,然后进行分析。在仪器外壳上的一点施加声源振动载荷(Y方向),输入声波的振动信号(见图 3)。为了减小边界效应对结果的影响,在两端各加长大于0.215 m(L/2),为了保证首波不受反射波干扰,而且保证电脑计算内存充足,将两端加长距离设为0.5 m。声系钢外壳两端为自由端。
|
| 图 3 载荷加载示意图 Fig.3 Schematic of loading |
为了与试验情况保持一致,避开筒体边缘,在隔声体的下端距离筒体本身30 mm处设置声波发射源(图 3中圆点处),上端设置多个接收器,利用接收器获得的数据与发射源处获得的数据就可以计算隔声量及表示时延量。
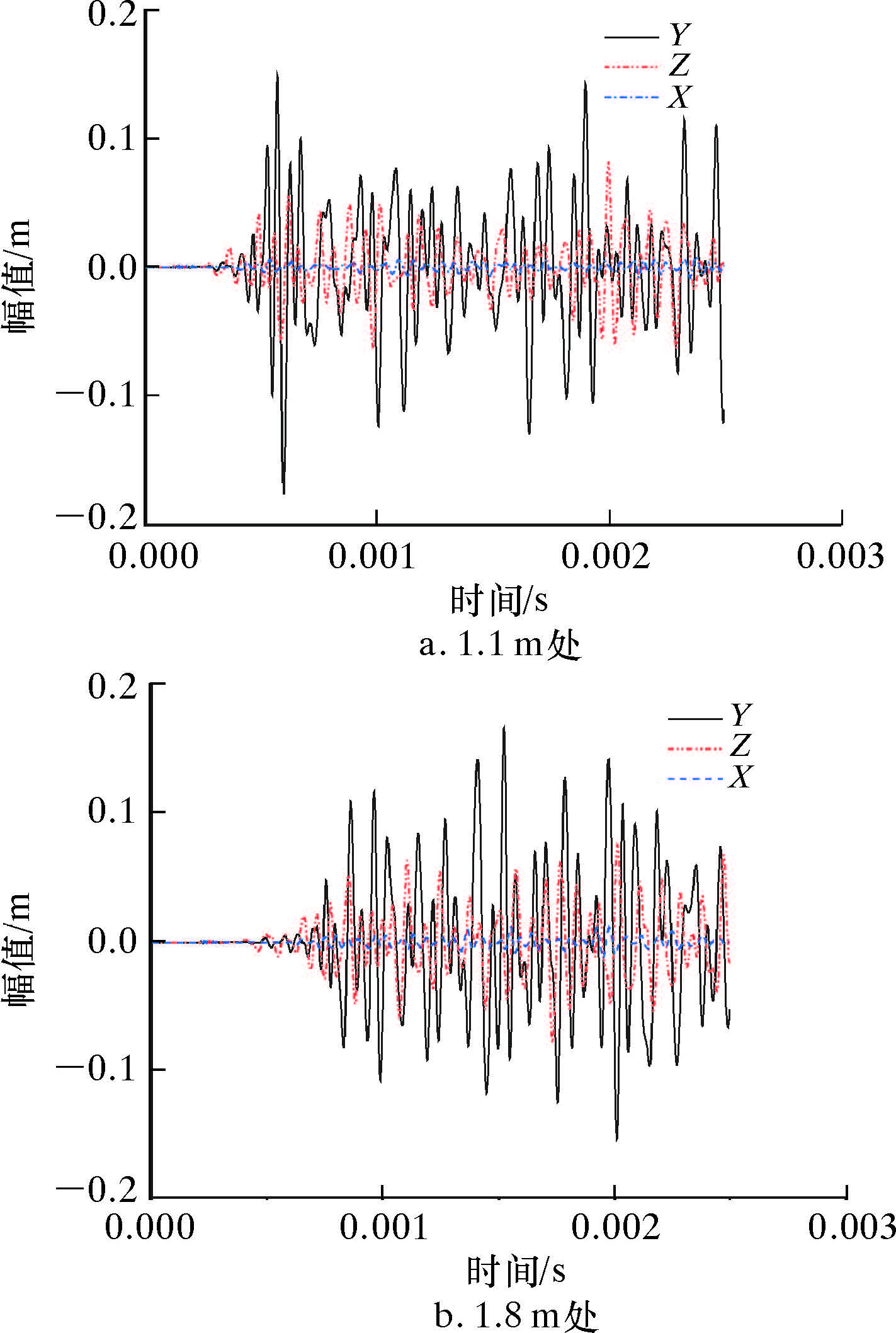
1.3 结果分析声波测井仪器的源距不能太短,否则不利于各种波形的分离,而声波会随着距离的增大而衰减,所以源距又不能太长;间距的选取不能太大,以避免空间假频及衰减,不能太小,否则会影响检测算法[6]。综合以上因素考虑,取源距为1.1和1.8 m 2处的波形图进行分析,2源距3个方向波形如图 4所示。由于声波的加载在Y方向,Y方向的首波到达时间要先于Z、X方向,并且Y方向波形的能量也比较大。由图 4可知,ANSYS分析的结果中,Y方向的波形幅值要高于Z和X 2个方向的波形幅值,而且1.8 m处的首波到达时间要迟于1.1 m处的首波到达时间。
|
| 图 4 2源距3个方向波形图 Fig.4 The waveforms from three directions of two sources |
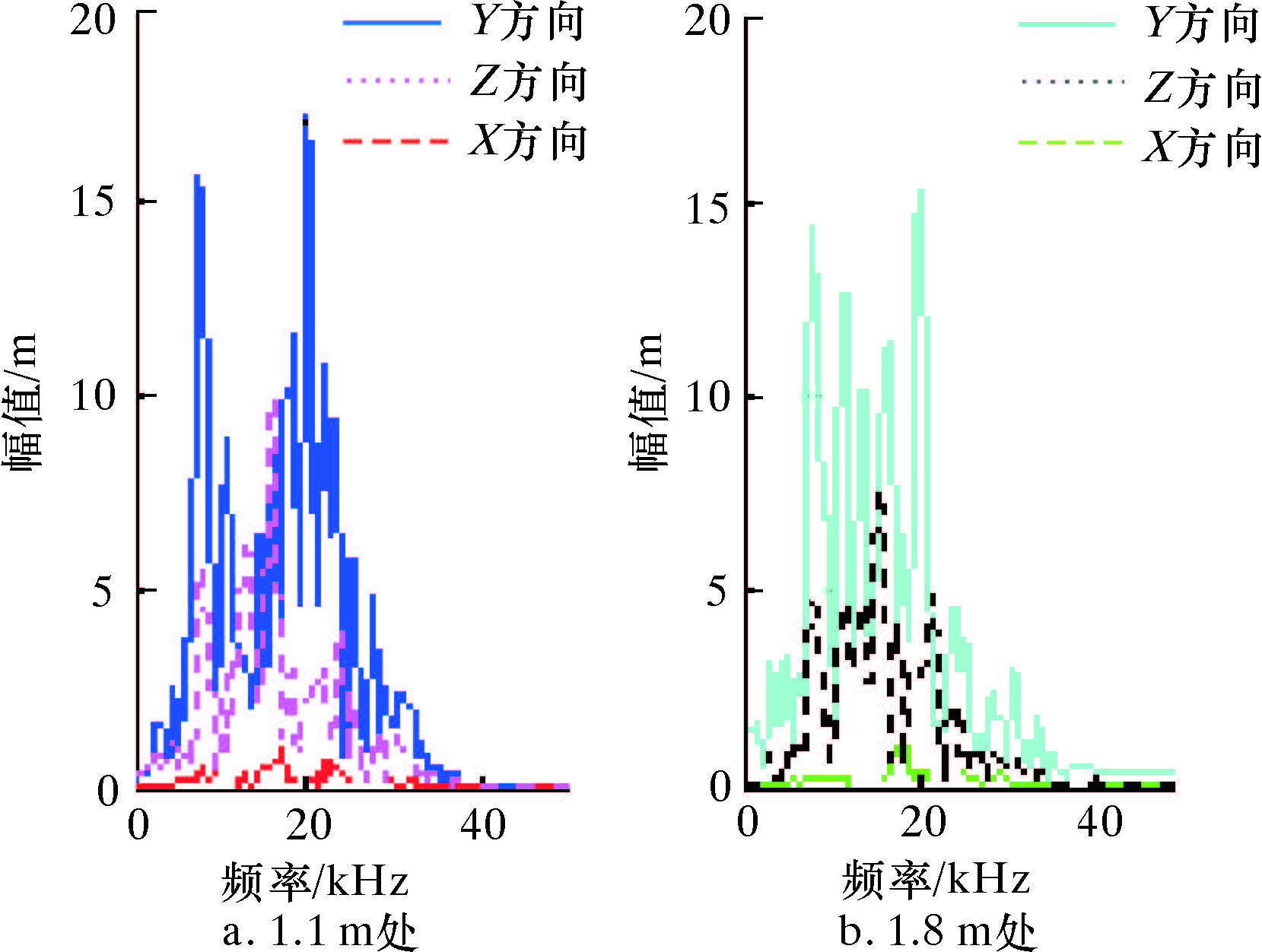
对2点处的波形数据进行快速傅里叶变化(FFT)处理[7],得到1.1和1.8 m 2处波形的频谱分析图,如图 5所示。由图可以看出,无槽隔声体的衰减程度并不明显。2点首波到达时间见表 1。由表可以看出,1.8 m处的波形与1.1 m处的波形相比,首波到时有一定的延迟,并且首波的幅值也有一定的衰减,2点处幅值对比见表 2。
|
| 图 5 2处信号波形的频谱分析 Fig.5 Spectrum analysis of the two signal waveforms |
| s | |||
| 位置 | Y方向 | Z方向 | X方向 |
| 1.1 m处 | 0.000 275 0 | 0.000 249 8 | 0.000 274 0 |
| 1.8 m处 | 0.000 408 0 | 0.000 411 0 | 0.000 488 6 |
| m | |||
| 位置 | Y方向 | Z方向 | X方向 |
| 1.1 m处(A1) | 7.641e-3 | 3.161e-3 | 2.243e-4 |
| 1.8 m处(A2) | 5.235e-3 | 1.934e-3 | 1.639e-4 |
因为当声波传播到隔声体的左、右两端,会发生多次反射,反射波和原来的波发生干涉时就会产生驻波。在某些特定的频率,其相位一致的时候,就会产生一个振幅较大的驻波,所以会出现长源距处的波形幅值高于短源距处的波形幅值的情况。
由表 1的数值可以估算纵横波的速度大小。由表 1中2点距离和波到达时间,估算出Y方向的波速为5 263 m/s,Z方向的波速为3 354 m/s,X方向的波速为3 262 m/s。
评价隔声体性能的物理量主要是隔声量,隔声量是某一振动分量的某一频率成分的幅度经过隔声体后的声衰减量[8]。
利用有限元软件ANSYS对隔声结构进行数值模拟的结果,可根据下面关于频率的隔声量计算公式进行衰减特性分析:
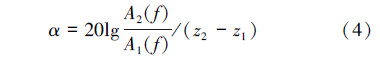
式中:α为隔声量,f表示频率,A1(f)、A2(f)分别为远、近接收器接收到频率为f的声波幅度,z1、z2为2个接收器的源距。
A1(f)、A2(f)可以由接收信号经快速傅里叶变换得到。2个接收器间距为0.1 m,选取每隔4个接收器的波形数据进行衰减分析,得到以频率为横坐标,衰减系数为纵坐标的图。对ANSYS分析得到的数据进行开窗处理,窗的起始点取首波到时,窗长取为900个数据长[6, 9]。利用Matlab软件进行编程处理。
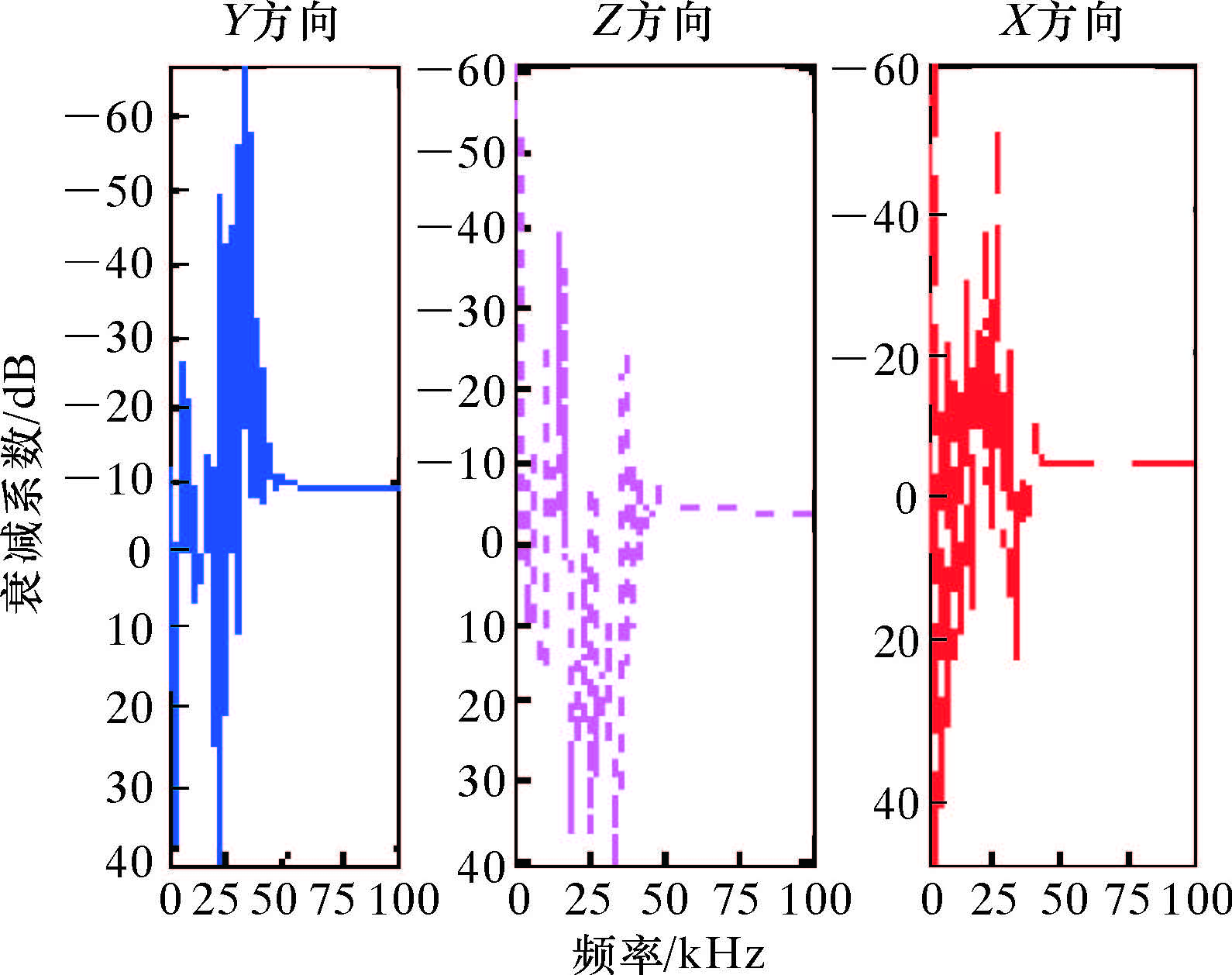
无槽隔声体的衰减系数如图 6所示。由图可以看出,Y方向的衰减系数要大于Z方向和X方向的衰减系数。由于分析结果中会有一些奇异点,所以会有衰减系数为正数的情况出现。
|
| 图 6 无槽隔声体3个方向的衰减系数 Fig.6 Attenuation coefficient of the acoustic insulator without groove in three directions |
评价隔声体性能的物理量是隔声量,隔声体结构的隔声量可由ANSYS模拟计算中的接收器接收到的时域波形信号分析得到。 声衰减量为[4]:
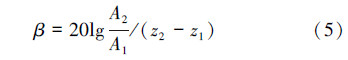
式中:A1、A2分别为远、近接收器的波形幅值。
根据公式(5)和表 2的数据,可以算出3个方向的衰减量。
计算Y方向的衰减时,取1.1和1.8 m 2处波形,A1=7.641×10-3 m,A2=5.235×10-3 m,z2=1.8 m,z1=1.1 m,代入式(5)中,得到衰减量10.804 6 dB/m。同理,得到Z方向的衰减量14.037 1 dB/m,X方向的衰减量8.946 2 dB/m。
由计算出的声波衰减系数和时延量来看,无槽筒体的隔声量不满足实际需要。因此,要对隔声体进行切槽处理或者研制其他类型的隔声体。
2 刻槽筒体隔声性能分析 2.1 刻槽筒体计算条件刻槽筒体外径104 mm,壁厚8 mm,长2.2 m。声波从下端(右端)传到上端(左端)。计算出声波传递过程中的衰减系数和传递时间。材料与声源均与无隔声槽筒体一致。
2.2 刻槽筒体建模数值模拟时,与无槽筒体一样,采用主频14 kHz的宽带雷克子波声源函数,见式(1)。
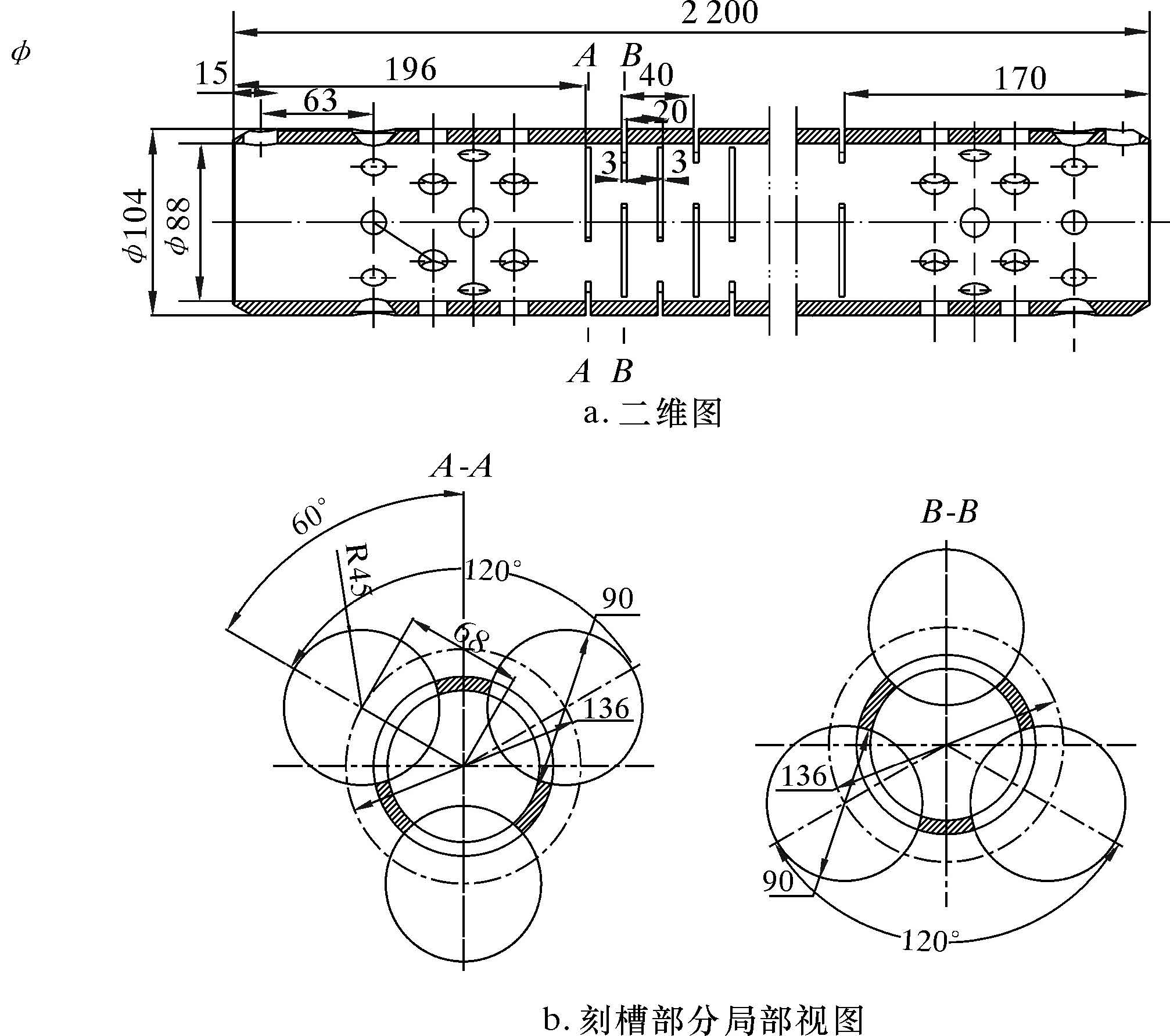
在三维建模软件Solidworks中建立刻槽筒体的三维结构图,如图 7所示。将三维模型导入到ANSYS中,同样采用Solid 185号单元划分网格。为了减小边界效应对结果的影响,与无槽筒体一样,在两端各加长0.5 m,筒体两端同样为自由端。图 8为刻槽筒体的局部图。

|
| 图 7 隔声体三维图 Fig.7 Three dimensional schematic of the acoustic insulator |
|
| 图 8 隔声体局部图 Fig.8 Partial view of the acoustic insulator |
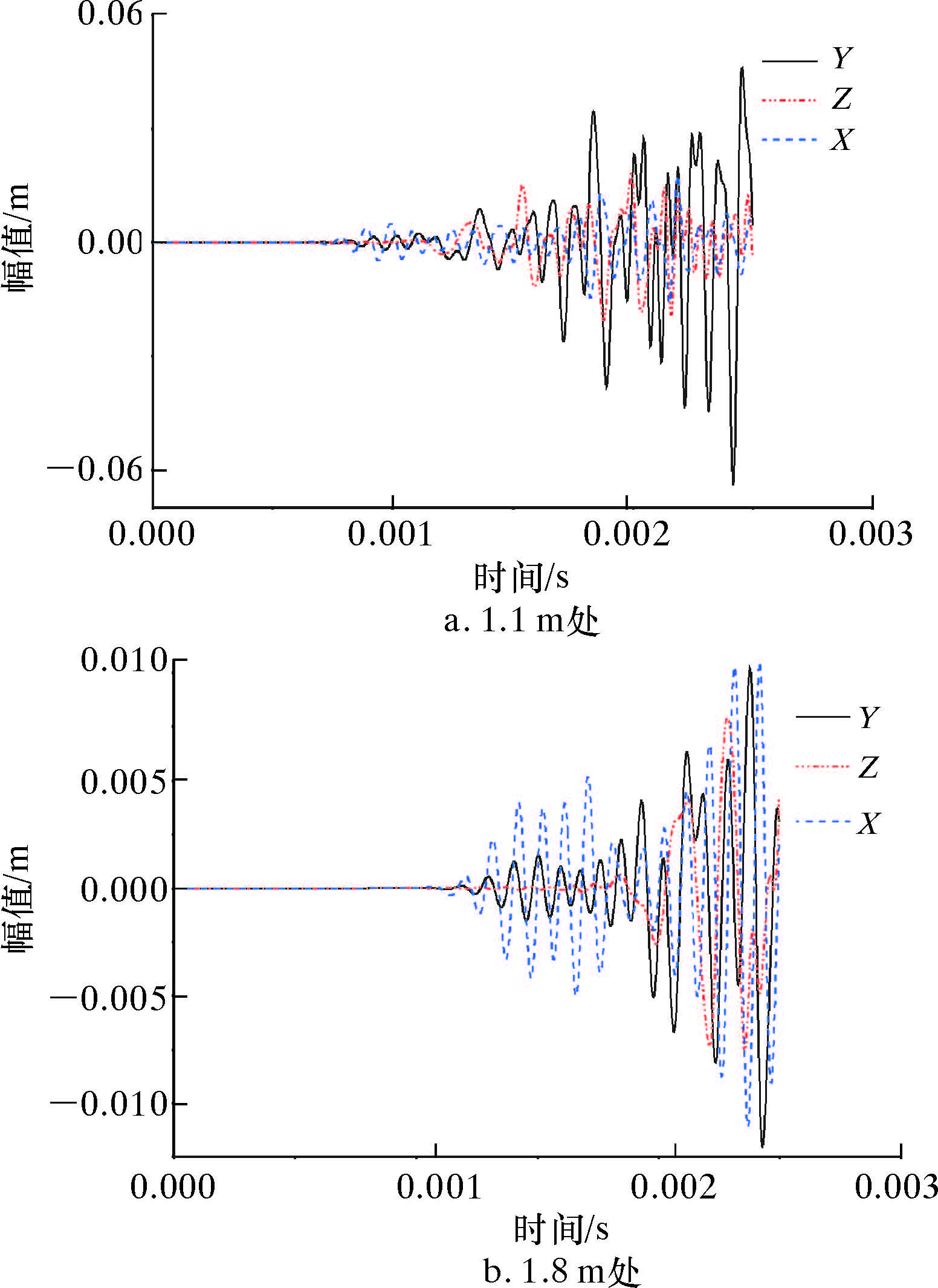
利用有限元软件ANSYS进行分析,取源距为1.1和1.8 m处的波形图,如图 9所示。由图可知2源距处首波的幅值,如表 3所示。
|
| 图 9 2源距3个方向波形图 Fig.9 The waveforms from three directions of two sources |
| m | |||
| 位置 | Y方向 | Z方向 | X方向 |
| 1.1 m处(A1) | 8.034e-3 | 5.660e-3 | 7.390e-4 |
| 1.8 m处(A2) | 3.911e-3 | 4.967e-3 | 4.242e-4 |
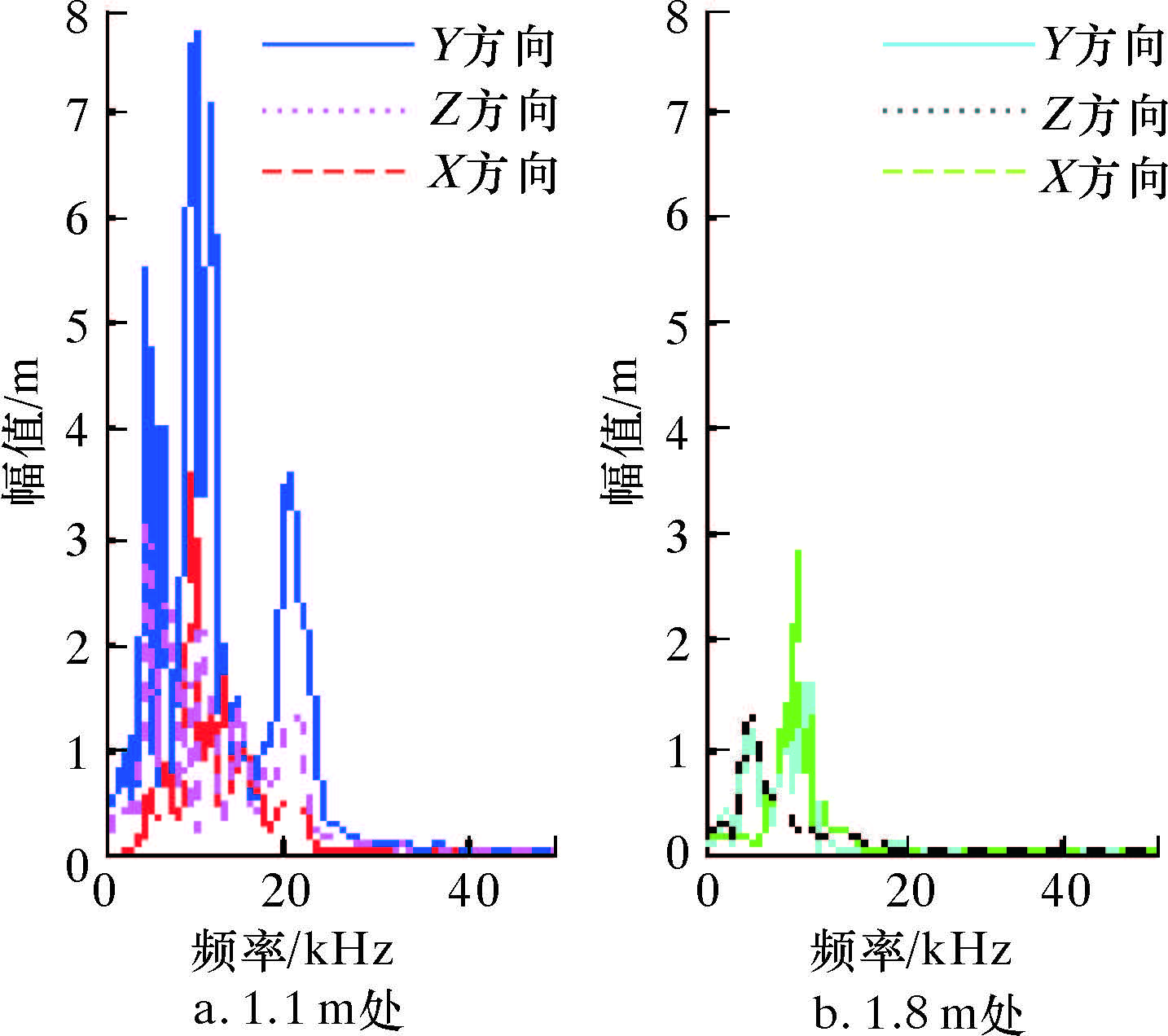
利用Matlab进行频谱分析,得到频谱分析图,如图 10所示。从图可以看出,Y方向的衰减最明显,而且高频段的衰减比低频段的衰减快。
|
| 图 10 2源距处3方向频谱分析图 Fig.10 Spectrum analysis of two sources in three directions |
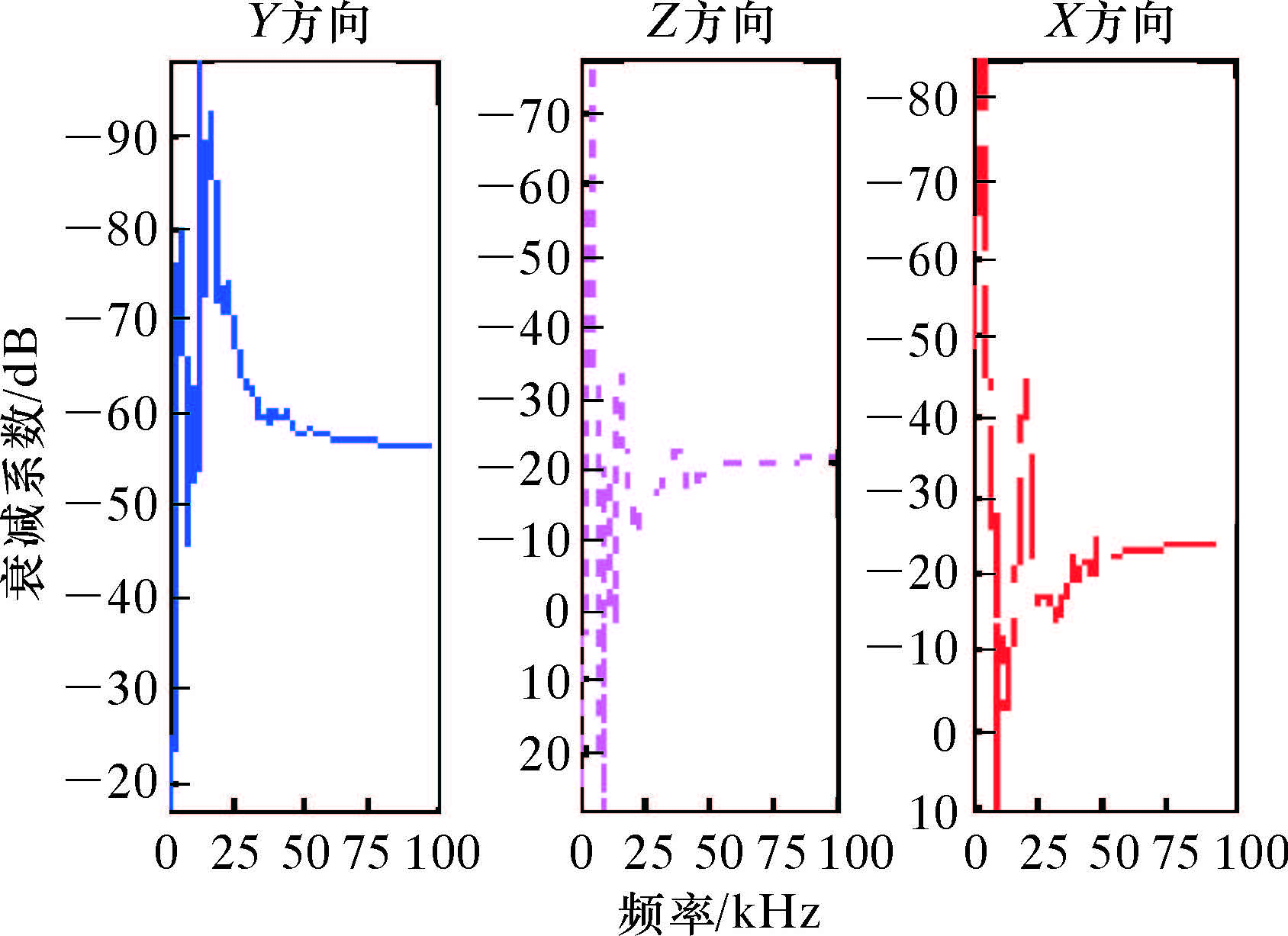
在1.1~1.8 m之间每隔0.1 m取1道波形,得到X、Y、Z 3个方向的阵列波形图,同样对ANSYS分析得到的数据进行开窗处理,窗的起始点取首波到时,窗长取为900个数据长。再利用MATLAB软件进行编程处理,可得到衰减系数图,如图 11所示。
|
| 图 11 刻槽隔声体3方向的衰减系数 Fig.11 Attenuation coefficient of acoustic insulator with groove in three directions |
由图 11可知,Y方向衰减系数大于Z方向和X方向的衰减系数。Y方向在约为14 kHz处达到最高值;Z方向在约为6 kHz处达到最高值,X方向在约为6 kHz处达到最高值。
声波在周期性刻槽隔声体上传播时在频率上会体现出通、阻带交替的状况[10]。在通带的频率范围,声波可顺利通过,在阻带的频率范围内,声波会发生衰减而不易通过。且通、阻带的位置只由周期性刻槽隔声体本身的结构参数决定[11, 12]。
根据式(5)和表 3的数据,可以算出3个方向的衰减量,得到表 4。
| 参数 | Y方向 | Z方向 | X方向 |
| 衰减量/(dB·m-1) | 43.697 0 | 24.366 7 | 15.860 5 |
| 时延量/s | 4.11e-4 | 5.03e-4 | 3.88e-4 |
声波测井仪外壳筒体是仪器受力的主体,本身要有足够的强度,但同时又希望外壳筒体能够有效隔离声波的传播,笔者主要对有、无隔声槽的外壳筒体的声传播特性进行了研究。衡量外壳筒体隔声效果的好坏有2个物理量,即隔声量和时延量[13]。隔声量是指某一振动分量的某一频率成份的幅度经过隔声体后的衰减量。时延量是指某一振动分量信号经过隔声体后的延迟时间。在2源距的波形图上可以直接读出源距为1.1 m和源距为1.8 m处的首波达到时间差值,即可作为隔声体的时延量[14]。
取有、无隔声槽上的同样长度,同样间隔的2个位置进行声波衰减的分析,分析结果如表 5所示。由表可知,有隔声槽的外壳隔声效果比无隔声槽的要好很多。加了隔声槽后,衰减系数增大了近2倍,延迟时间也有了改进。这说明带隔声槽的隔声体更能有效地阻止声波在仪器内部或仪器表面直接从发射端向接收端传播。
| 条件 | 衰减系数/(dB·m-1) | 时延量/s | ||
| X方向 | Y方向 | Z方向 | ||
| 无槽 | 8.946 2 | 10.804 6 | 14.037 1 | 1.29e-4 |
| 有槽 | 15.860 5 | 43.697 0 | 24.366 7 | 3.88e-4 |
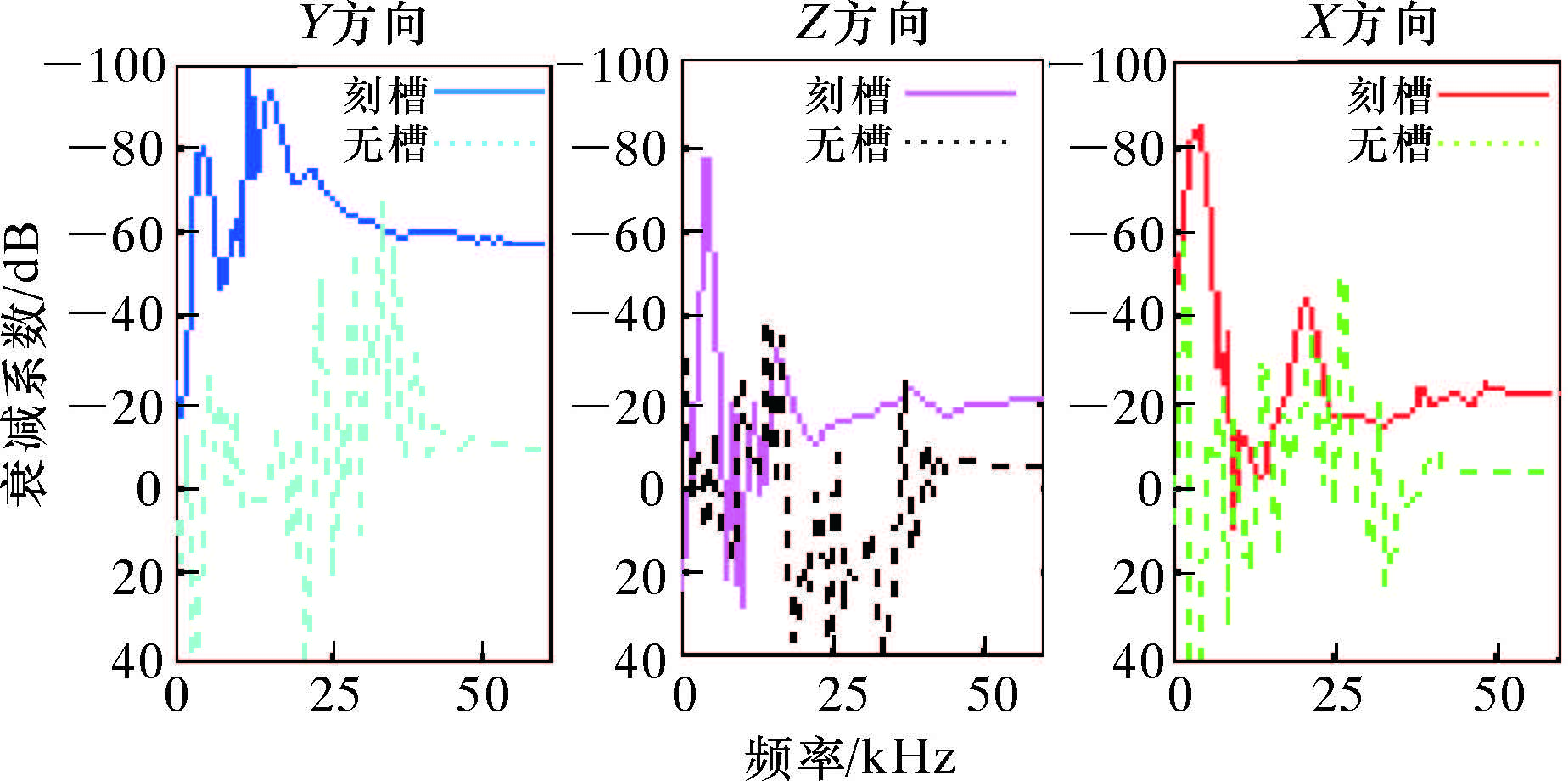
图 12为无隔声槽和有隔声槽的衰减系数曲线对比。由图可知,刻槽的隔声体的隔声效果明显优于无槽隔声体。
|
| 图 12 3方向衰减系数对比图 Fig.12 Comparison of attenuation coefficients o the acoustic wave from three directions |
声波测井最常使用的频率是2 kHz以上的频段,筒体的隔声量基本上达到40 dB/m以上;在2 kHz以下的频段内,特别是在500~1 000 Hz频段内,筒的隔声量最小值处不到10 dB/m[4]。因此,刻槽筒体的隔声性能满足要求。对于无槽筒体,可通过改变槽的宽度或者一周的隔声槽数量来改善筒体的声传播性能[15]。
4 结 论(1)建立了声波测井仪外壳筒体声传播特性计算模型,计算分析了有、无隔声槽的外壳筒体的声传播特性。
(2)无隔声槽的外壳筒体的隔声效果不满足实际需要,有隔声槽的外壳筒体的隔声效果很好,对声波的延时也满足要求。
(3)有隔声槽外壳筒体的隔声效果明显优于无隔声槽外壳筒体的隔声效果,并满足测井要求。
| [1] | 张晓波,高辉,张剑.现代声波测井技术应用[J].石油仪器,2014,28(1):1-1. |
| [2] | 罗学东,李玉霞,王国锋,等.MPAL多极子阵列声波测井仪新型隔声体研究[J].石油仪器,2009,23(5):16-18. |
| [3] | 李玉霞,李亚敏.MPAL多极子阵列声波测井仪[J].测井技术,2008,32(5):439-442. |
| [4] | 乔文孝,马文中.隔声体性能评价的方法研究[J].测井技术,2002,26(2):104-106. |
| [5] | 张秀辉,胡仁喜,康士廷.ANSYS 14.0有限元分析从入门到精通[M].北京:机械工业出版社,2013. |
| [6] | 钟剑.阵列声波测井属性信息提取方法研究[D].成都:西南石油大学,2011. |
| [7] | 张丰德.详解MATLAB数字信号处理[M].北京:电子工业出版社,2010. |
| [8] | 闫向宏,苏远大,孙建孟,等.周期性轴对称凹槽结构隔声特性数值模拟[J].计算物理,2010,27(6):869-876. |
| [9] | 王华,陶果,张绪健.随钻声波测井研究进展[J].测井技术,2009,33(3):197-203. |
| [10] | 张美玲.随钻声波测井仪器隔声体的数值模拟研究[D].东营:中国石油大学(华东),2011. |
| [11] | 庄春喜.随钻声测井隔声体数值模拟与实验研研究[D].东营:中国石油大学(华东),2011. |
| [12] | 苏远大,庄春喜,唐晓明.随钻声波测井钻铤模式波衰减规律研究与隔声体设计[J].地球物理学报,2011,54(9):2419-2428. |
| [13] | 苏远大,庄春喜,邓林,等.随钻声波测井隔声体性能评价实验研究[J].测井技术,2011,35(5):402-405. |
| [14] | 刘彬,王芳,陈德华,等.周期性非轴对称孔槽结构隔声性能数值模拟研究[J].应用声学,2012(5):3. |
| [15] | 杨勇,车小花,张菲,等.用三维时域有限差分法研究随钻声波测井仪器隔声体的设计[J].科学技术与工程,2009,9(3):565-567. |



