0 引 言
海洋天然气增压集输技术的发展对海洋大功率往复式压缩机的振动性能提出了更高的要求,对低振幅振动特性的需求更加迫切。然而,往复式压缩机曲轴对其整机振动特性具有重要影响,大功率工况下低振幅振动特性的曲轴将逐渐成为各国学者的研究热点。
为缩短设计周期和降低成本,国内外学者多采用计算机仿真技术来模拟往复式压缩机曲轴的振动特性。例如,A.Okamura[1]首先应用有限单元法研究了曲轴的振动特性。Z.P.Mourelatos[2]采用有限单元法研究了曲轴系统的振动特性。马星国等[3]使用有限单元法研究了一个工作循环周期内曲轴的动态响应。李小华等[4]则采用有限单元法对曲轴的振动特性进行了预测。 从目前的研究工作来看,往复式压缩机曲轴的优化设计研究相对较少。H.Simon等[5]在建立曲轴有限元模型的基础上,用最优化的方法对系统的振动特性进行了修改。李磊等[6]建立了曲轴-连杆-活塞的三维参数化模型,采用多学科优化方法对系统进行了结构轻量化设计,但没有考虑曲轴的振动特性。
在有限元分析中,模态是设计参数的隐式函数,二者之间没有明确的表达式,因而难以对其直接进行优化。针对上述问题,笔者考虑了润滑油道直径的影响,对海洋大功率往复式压缩机曲轴进行动态建模,通过拉丁超立方试验方法采样,结合椭圆基网络构建曲轴振动特性的神经网络代理模型,以曲轴几何结构参数和润滑油道直径为设计变量,以曲轴第3阶、第5阶和第7阶模态振型最大振型因子为设计目标,采用具有多岛效应的遗传算法对神经网络代理模型进行优化。研究结果表明,采用该方法对曲轴进行优化能够有效改善曲轴的振动特性。
1 曲轴的建模与计算 1.1 海洋大功率往复式压缩机结构海洋大功率往复式压缩机结构如图 1所示。工作时,曲轴动作,通过连杆带动活塞做往复直线运动,依靠活塞室和进、排气管道压差的变化实现进、排气阀的动作,最终实现天然气的压缩。

|
| 图 1 海洋大功率往复式压缩机 Fig.1 The ocean high-power piston compressor 1—机体; 2—十字头; 3—连杆; 4—曲轴; 5— 活塞杆;6—进气阀;7—活塞;8—排气阀。 |
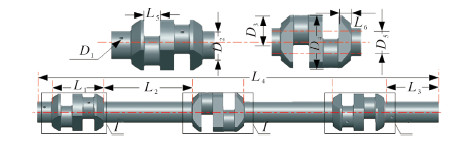
海洋大功率往复式压缩机曲轴模型如图 2所示。基体材料为42CrMo,弹性模量210 GPa,泊松比0.3,密度7.9 g/cm3。
|
| 图 2 往复式压缩机曲轴模型 Fig.2 The model of piston compressor crankshaft |
曲轴的自由模态由其材料属性和结构尺寸共同决定[6]。设计L1=439.00 mm,总长L4=3 263.00 mm,D2=171.45 mm,D3=177.80 mm,其他结构参数包括L2、L3、L5、L6;截面直径D4、D5,润滑油道直径D1。根据以上结构参数可以确定往复式压缩机曲轴的结构。考虑到标准件尺寸,最终确定设计优化模型的变量为:
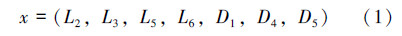
曲轴振动属于多自由度受迫振动,可用基于达朗贝尔原理的受迫振动方程来描述:
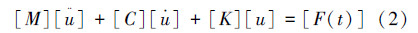
使用模态叠加法解此方程,需变换坐标对其进行解耦。首先需要求解出系统的固有频率和振型:

当体系有N个自由度时,ωi和{φ}i 分别表示第 i 阶自振圆频率和振型,i=1,2,……,N。
由于线性方程的齐次性,式(3)无法求得振型向量元素的绝对值,只能求得振型的形状。按特定元素归一化方法得到振型分布的振型因子,即有:

对于不同的i、j可以任意选定。归一化后依次排列成矩阵[φ],并对式(2)进行变换后可得:
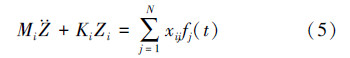
式中,Mi为模态质量矩阵[M]=[φ]T[M][φ]第i行的元素,Ki为模态刚度矩阵[K]=[φ]T[K][φ]第i行的元素,Zi为模态坐标矩阵[Z]第i行的元素,xij为振型归一化矩阵[φ]中对应元素,fj(t)为激励力矩阵[F(t)]中对应的j列元素,t为时间。
由式(5)可得模态坐标响应,逆变换后可得物理坐标下的响应[u]。由式(1)~式(5)可知,模态振型分布对于响应[u]计算有着重要影响。由于模态振型由一系列无量纲的模态振型因子决定,故初步选取往复式压缩机曲轴前7阶模态振型最大振型因子为优化目标,以改善模态振型分布。
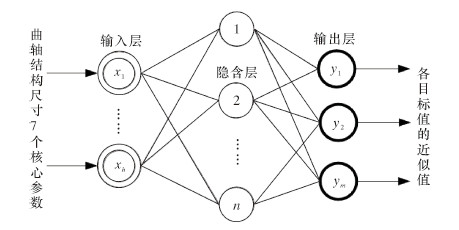
2 曲轴优化设计 2.1 构建神经网络代理模型基于有限元的曲轴模态模拟计算工作量大,抽样点太多,因此采用拉丁超立方试验设计方法获取样本点[7, 8]。椭圆基网络具有很强的逼近复杂非线性函数的能力、黑箱特点和极好的泛化能力,无需数学假设,学习速度快[9],故构建曲轴振动特性关于其结构尺寸的椭圆基网络代理模型,见图 3。
|
| 图 3 椭圆基神经网络结构模型 Fig.3 The ellipse based neural network model |
由构建的h个输入值、n个隐层节点和m个输出值得椭圆基网络代理模型表达式为:
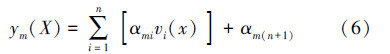
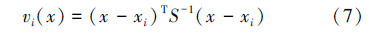
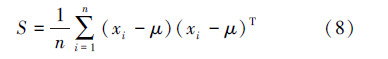
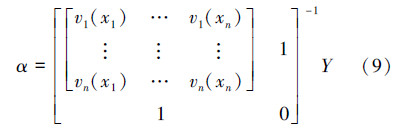
结合式(1)和式(6)~(9)即可求得曲轴自由模态振型关于其结构尺寸的椭圆基神经网络代理模型。在曲轴的设计域内选择20组样本点,如表 1所示。对照样本点修改曲轴结构尺寸并进行模态分析,得到前7阶模态振型最大振型因子,见图 4。
| mm | |||||||
| 试验次数 | L2 | L3 | L5 | L6 | D1 | D4 | D5 |
| 1 | 726.8 | 435.7 | 97.0 | 73.5 | 15.575 | 330.2 | 76.75 |
| 2 | 718.0 | 441.1 | 99.8 | 74.1 | 16.175 | 334.2 | 76.45 |
| 3 | 720.4 | 441.7 | 95.0 | 74.3 | 14.075 | 334.6 | 75.55 |
| 4 | 719.6 | 433.3 | 98.2 | 71.7 | 15.875 | 335.4 | 77.95 |
| 5 | 730.0 | 437.5 | 96.2 | 71.9 | 14.375 | 332.2 | 73.45 |
| 6 | 727.6 | 438.1 | 93.4 | 72.3 | 16.925 | 336.2 | 77.35 |
| 7 | 730.8 | 440.5 | 98.6 | 73.3 | 15.725 | 335.8 | 78.25 |
| 8 | 722.8 | 439.3 | 97.4 | 72.1 | 16.775 | 337.4 | 73.15 |
| 9 | 716.4 | 444.1 | 93.0 | 71.1 | 14.975 | 333.8 | 77.05 |
| 10 | 718.8 | 433.9 | 99.0 | 74.7 | 14.825 | 336.6 | 74.05 |
| 11 | 717.2 | 438.7 | 94.6 | 72.5 | 15.275 | 335.0 | 73.75 |
| 12 | 728.4 | 439.9 | 99.4 | 71.3 | 14.675 | 331.4 | 74.95 |
| 13 | 731.6 | 436.9 | 92.2 | 74.5 | 15.425 | 337.0 | 74.65 |
| 14 | 723.6 | 442.3 | 95.4 | 74.9 | 16.325 | 330.6 | 75.25 |
| 15 | 721.2 | 434.5 | 92.6 | 73.9 | 15.125 | 333.4 | 78.85 |
| 16 | 725.2 | 435.1 | 95.8 | 71.5 | 16.625 | 332.6 | 75.85 |
| 17 | 726.0 | 444.7 | 93.8 | 73.1 | 16.475 | 333.0 | 74.35 |
| 18 | 724.4 | 442.9 | 96.6 | 73.7 | 16.025 | 331.0 | 77.65 |
| 19 | 722.0 | 436.3 | 94.2 | 72.9 | 14.525 | 331.8 | 76.15 |
| 20 | 729.2 | 443.5 | 97.8 | 72.7 | 14.225 | 337.8 | 78.55 |
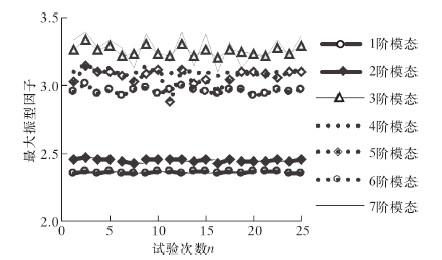
|
| 图 4 前7阶模态振型最大振型因子试验结果 Fig.4 The test results of the maximum modal shape factor of the first seven order modal shape |
由图 4可知,受曲轴结构尺寸影响较大的为第3阶模态振型最大振型因子,2阶弯曲振动;第5阶模态振型最大振型因子为3阶弯曲振动与扭转振动的组合;第7阶模态振型最大振型因子为3阶弯曲振动。而其余模态振型最大振型因子基本上保持不变,故选取第3阶、第5阶和第7阶模态振型最大振型因子为设计目标,构建关于其结构尺寸的椭圆基神经网络代理模型。
2.2 模型拟合优度分析由于椭圆基函数近似模型无法直接给出具体的输入变量与相应目标之间的函数关系,为获得最佳的近似模型,引入复相关系系数R2来评价各模型的近似程度。R2越接近1时,说明代理模型的拟合优度越好。复相关系系数为:
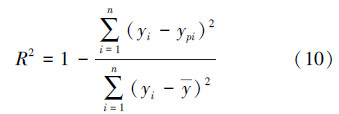

将设计目标响应值和预测值代入式(10)与式(11),得各模型拟合优度,如图 5所示。
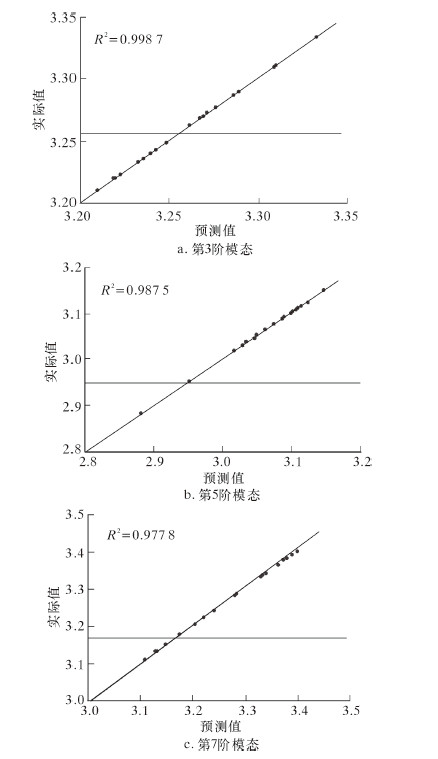
|
| 图 5 各阶模态振型最大振型因子近似模型的拟合优度效果图 Fig.5 The fit goodness of the maximum modal shape factor approximate model of each order modal shape |
从图 5可见,第3阶、第5阶和第7阶的椭圆基神经网络近似模型的决定系数都在0.97以上,表明基于椭圆基神经网络建立的近似模型能够很好地映射设计变量与设计目标之间的关系,各设计变量近似模型精度较高,可直接用于下一步的优化设计。
2.3 优化设计以曲轴几何结构参数和润滑油道直径为设计变量,以曲轴第3阶、第5阶和第7阶模态振型最大振型因子为设计目标,则海洋大功率往复式压缩机曲轴的优化数学模型可表示为: minf3(x),f5(x),f7(x)
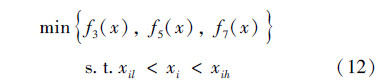
| mm | |||||||
| 设计变量 | L2 | L3 | L5 | L6 | D1 | D4 | D5 |
| 初始值 | 724.0 | 439.0 | 96.0 | 73.0 | 16.0 | 334.0 | 76.2 |
| 上限 | 716.0 | 433.0 | 93.0 | 71.0 | 14.0 | 330.0 | 73.0 |
| 下限 | 732.0 | 445.0 | 99.0 | 75.0 | 17.0 | 338.0 | 79.0 |
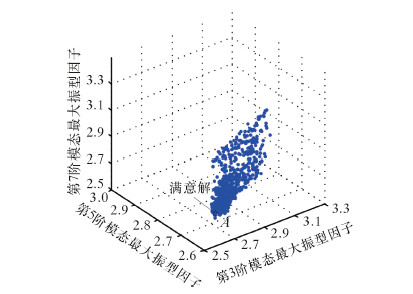
多目标优化问题各子目标可能存在交互作用,无法同时达到最优,只能通过折中处理,获取Pareto最优解集[10]。采用具有多岛效应的遗传算法寻优,求取Pareto前沿。设定各子目标权重均为1,初始种群数量20,岛数10,最大遗传代数10,交叉概率1.0,变异概率0.01,移民概率0.01,移民间隔5。经过2 000次迭代后得到的Pareto前沿解分布如图 6所示。
|
| 图 6 Pareto前沿解分布图 Fig.6 Distribution of the Pareto frontier solutions |
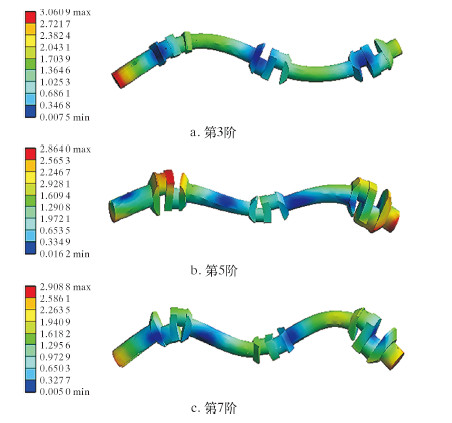
选取A点作为满意解,优化后最终结果如表 3所示。结果显示,采用具有多岛效应的遗传算法对椭圆基神经网络近似模型寻优并值调整,代入有限元模型,造成第3阶、第5阶和第7阶模态振型最大振型因子误差分别为0.26%、9.00%和10.40%,这表明该优化方法有效。与初始值相比,第3阶、第5阶和第7阶模态振型最大振型因子分别下降了6.0%、6.9%和11.9%。曲轴的前7阶模态振型分布得到了有效改善。 优化后曲轴第3阶、第5阶和第7阶模态振型如图 7所示。第3阶模态为2阶弯曲振动,第5阶模态为3阶弯曲振动与扭转振动的组合,第7阶模态为3阶弯曲振动。振动频率依次为168.57、282.91和452.22 Hz。
| mm | |||
| 设计变量 | 初始值 | 寻优值 | 最终取值 |
| L2 | 724.00 | 731.22 | 731.20 |
| L3 | 439.00 | 434.73 | 434.70 |
| L5 | 96.00 | 93.03 | 93.00 |
| L6 | 73.00 | 73.76 | 73.80 |
| D1 | 16.00 | 14.72 | 14.72 |
| D4 | 334.00 | 336.74 | 336.74 |
| D5 | 76.20 | 73.03 | 73.00 |
| f3 | 3.258 | 3.069 | 3.061 |
| f5 | 3.098 | 2.646 | 2.884 |
| f7 | 3.300 | 2.634 | 2.909 |
|
| 图 7 第3阶、第5阶和第7阶模态振型图 Fig.7 The shape diagram of the third-order,fifth-order and seventh-order modal |
(1)将椭圆基神经网络引入到海洋大功率往复式压缩机曲轴模态振型优化设计中,构建了以曲轴几何结构参数和润滑油道直径为设计变量,曲轴第3阶、第5阶和第7阶模态振型最大振型因子为设计目标的曲轴优化近似模型,减少了计算工作量。
(2)对曲轴的分析和优化结果表明,基于椭圆基神经网络的海洋大功率往复式压缩机曲轴模态振型优化设计,可有效降低曲轴模态振型的最大振型因子,改善曲轴模态振型的分布,为整机振动特性分析和样机试验提供设计参数和理论依据。
| [1] | Okamura A.Experimental study of the correction between crankshaft vibration,engine-structure vibrations and engine noise in high speed engines[R].SAE951290,1995. |
| [2] | Mourelatos Z P.A crankshaft system model for stuctural dynamic analysis of internal combustion engines[J].Computers & Structures,2001,79:2009-2027. |
| [3] | 马星国,尤小梅,闻邦椿.基于虚拟样机技术的曲轴多体动力学仿真[J].振动与冲击,2008,27(9):155-157. |
| [4] | 李小华,沈贝,蔡忆昔,等.4105型柴油机曲轴计算模态与试验模态的振型相关性[J].农业工程学报,2011,27(11):51-55. |
| [5] | Simon H,Yung-Li L,Hong-Tae K,et al.Optimization of a crankshaft rolling process for durability[J].International Journal of Fatigue,2009,39:799-808. |
| [6] | 李磊,张建润,陈琳.柴油机运动机构多学科协同优化设计[J].农业机械学报,2013,44(3):33-36. |
| [7] | Koetniyom S,Brooks P C,Barton D C.The development of a material model for cast iron that can be used for brakesystem analysis[J].Proc.Instn.Mech.Engrs,Part D:JAutomobile Engineering,2002,216:349-362. |
| [8] | 吕辉,于徳介,谢展,等.基于响应面法的汽车盘式制动器稳定性优化设计[J].机械工程学报,2013,49(9):56-59. |
| [9] | 贾志新,张宏斌,郗安民.基于径向基函数神经网络的电火花线机床可靠性数据模拟生成[J].机械工程,2010,46(2):145-149. |
| [10] | 雷德明,严新平.多目标智能优化算法及其应用[M].北京:科学出版社,2009:1-33. |



