2. 中国石油天然气勘探开发公司;
3. 中国石油大学(北京);
4. 中石油昆仑燃气有限公司(涿州)
2. China National Oil & Gas Exploration and Development Corporation;
3. China University of Petroleum (Beijing);
4. PetroChina Kunlun Gas Co., Ltd.(Zhuozhou)
0 引 言
钻井参数优化设计是指在实际钻井生产作业过程中,有许多需要考虑和设置的参数,包括机械参数(如钻压、转速等)和水力参数(如泵压、排量、泵冲等),寻找到这些参数的最优组合,使得钻井工程的经济效益最大化的设计方案。钻井参数优选作为钻井设计中重要的环节,对于提高钻井经济效益具有重要作用。传统方法是用经验公式修正杨格模式,解析性较好,与实际钻井情况符合率较高,但数学推导计算较为复杂,需要人工干预,效率较低。近年来也有学者提出基于可钻性表示的钻速模型和钻井参数实时优选目标函数[1, 2, 3, 4],但应用结果都不太理想。笔者通过分析数据挖掘分类算法,提出了解决非线性多元函数优化问题的改进算法。基于模式搜索的遗传混合算法改善了自适应遗传算法局部寻优精度较差的缺陷,既具有较强的全局搜索能力,又提高了局部寻优精度。采用遗传算法和模式搜索的组合模型对钻井参数优化方法进行研究,结合遗传算法较强的全局搜索能力和模式搜索法局部寻优精度高的特点,寻找出最优的钻井参数组合。相比常规设计中根据经验试算并优选方案的方法,新方法更加高效,可直接确定给定条件下的最优方案。
1 钻井参数优化模型钻井参数优选目的是找寻使钻井过程达到最佳的技术经济效果的钻井参数配合,因此需要确立最优钻井目标函数,既能反映各参数对钻井过程的影响规律,又可以衡量钻井技术经济效果,满足该目标函数极值条件的参数配合即为最优钻井参数组合。
1.1 目标函数衡量钻井过程整体技术经济指标的函数有很多,比较常用和直观的是以钻井单位进尺成本作为钻井参数优选的评价指标[4],其表达式为:

式中,Cpm为进尺成本(单位),元/m;Cb为钻头成本,元;Cr为钻机作业费,元/h;t为钻进时间;tt为起下钻与接单根时间,h;H为钻头进尺。
式(1)是在只考虑了钻头成本与钻机作业费的情况下对问题进行分析与求解,不考虑钻井液和钻具组合等成本。
经过修正的杨格(F.S.Young)模式钻速方程如下:
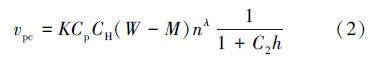
式中,vpc为机械钻速,m/h;W、M分别为钻压和门限钻压,kN;n为转速,r/min;K为地层可钻性系数;Cp、CH分别为压差影响系数和水力净化系数;λ为转速指数;C2为钻头牙齿磨损系数;h为牙齿磨损量,0≤h≤1。
式(2)可转换为钻头工作时间与钻头进尺的关系式:

钻头牙齿磨损方程表达式为:

即

式中,Af为地层研磨性系数;a1、a2为转速影响系数,由钻头类型决定;Z1、Z2为钻压影响系数,与钻头直径有关;C1为牙齿磨损减慢系数。
将以上公式进行积分变换,令 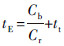 ,整理得到目标函数:
,整理得到目标函数:

式中,TE为钻头与起下钻成本的折算时间;hf表示牙齿的最终磨损量,即钻头寿命所对应的牙齿磨损量。由式(6)可以看出,在进行钻井参数优选时,应使CH和Cp的值尽量大。在目前水力喷射钻井条件下,水力喷射不仅能够满足净化井底的要求,而且能够进行水力破岩,帮助提高钻速,故可认为在满足携岩最低排量时,可近似取CH=1。而井底压差通过调节排量可以达到或趋于0,即可近似取Cp=1。这样,就得到含有钻压W、转速n、起钻时钻头磨损量hf 3个变量的目标函数:

在实际钻井工程中,目标函数所包含的自变量要满足一定的约束条件,包括各自的取值范围以及变量间的关系,只有在这些限制条件下获得的最优参数配合才有意义。
对目标函数(7)中各个变量进行约束条件分析可得:
(1)钻压W,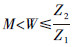 ,且W>0;
,且W>0;
(2)钻速n,0<n<nmax,其中nmax为钻井装置最大转速;
(3)牙齿磨损量hf,0≤hf≤1;
(4)钻压、转速乘积约束条件,Wn<PD,其中PD是钻头厂家推荐的最大允许Wn值;
(5)轴承磨损Bf,0≤Bf≤1。
对于同一个钻头,其工作寿命不仅是牙齿磨损量的函数,也是轴承磨损量的函数,即有:

联立式(5)和式(8)可得:

式中,b为轴承工作系数,与钻头类型和钻井液性能有关。
1.3 数学模型建立式(7)作为钻井参数优化的目标函数,求其在各变量约束条件下的最小值即得到最优参数组合,可以考虑为不等式约束条件下非线性规划问题,其多元优化数学模型为:

在遗传算法中,选定了目标函数后,需确定适应度函数,用于对当前种群中的个体优劣程度进行评价,是遗传算法个体评价的唯一指标,适应度越高的值越接近目标函数最优解。适应度函数应满足单值、连续、非负和最大化的要求。由于钻井参数优选目标函数是以求取最小值为目的,且目标函数值域为正实数空间,所以构造个体适应度函数F:

遗传算法是以达尔文的自然选择学说为其基本思想,模拟生物遗传和进化进程的一种计算模型[5, 6, 7]。遗传算法的基本理论思想是随机产生一系列待选解,即染色体(Chromosome),形成一个种群,其中每个个体代表一组解,由一组基因(Gene,染色体值)组成的串结构来表示,通过某一特定标准对个体进行评价,保留性能好的,淘汰性能差的,并且允许各组解之间通过信息交叉或变异产生新的解集,再进行评价优选,如此重复下去,直到得到符合标准要求的解。遗传算法包括选择、交叉和变异等3种基本操作,它们也被称为遗传算子。
遗传算法全局寻优搜索能力比较强,能够解决目标函数全局优化问题,但是遗传算法对于局部寻优精度较差,如果使用单一的遗传算法,很难得到最优的参数组合。而模式搜索法局部寻优精度好,并且遗传算法具有很好的可扩展性,通过这2种算法的混合使用,能够取长补短,优选出精度更高的参数组合。
2.2 模式搜索法原理模式搜索法是一种无需导数优化(Derivative Free Optimization,DFO)方法,一般沿着坐标方向集逐次循环进行搜索,并验证该方向是否为下降方向,得出下一个迭代点[8]。
2.3 改进遗传算法模型模式搜索法是一种求解效率很高的无需导数优化(Derivative Free Optimization,DFO)方法,并且不需要计算搜索方向,而遗传算法(Genetic Algorithm,GA)本身也是一种用于解决优化问题的无需导数算法,所以如果将两种算法结合,所得到的混合算法既能够拥有遗传算法的全局大范围搜索能力,也可以获得模式搜索法局部寻优能力强的能力,并且混合算法仍然是一种DFO方法。
2.4 基于改进遗传算法钻井参数优选 2.4.1 种群初始化针对所要解决的钻井参数优化问题,选用实数编码,因为这种编码方式不需要将实数数值转化为二进制等基因型串结构数据,而是直接在表现型数据上进行各个算子的运算操作,每个染色体即为一个实数向量。
2.4.2 选择操作对种群中的个体染色体分别计算适应度值,按照选择概率选取优良个体进入下一代种群。个体适应度值越高,被选中的概率就越大。笔者选取轮盘赌法进行选择操作,是基于适应度比例的选择策略,个体i被选中的概率为:

式中,Fi为个体i的适应度值;N为种群个体数目。
2.4.3 交叉操作将选择操作后的新种群中的个体两两配对,将其某个或某段基因段进行交叉互换,将父代的优秀基因得以保留,并遗传到下一代。采用实数对个体编码,用实数交叉法进行交叉操作,则第k个染色体ak和第l个染色体al在第j位的交叉操作方法为:

式中,b为[0,1]区间随机数。
交叉概率采用自适应遗传算法解决方法,按式(14)进行交叉概率取值操作:

从种群中随机选择个体,并按照变异概率让染色体基因位上的基因进行变异,模仿生物界中的变异现象,得到新的个体,以保证种群中个体的多样性。在实数编码中,第i个个体的第j个基因aij进行变异的操作方法为:

式中,amax是基因aij的上界;amin是基因aij的下界; 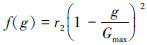 ,r2是一个随机数,g是当前迭代次数,Gmax是最大进化次数;r为[0,1]区间的随机数。
,r2是一个随机数,g是当前迭代次数,Gmax是最大进化次数;r为[0,1]区间的随机数。
变异概率自适应遗传算法解决方法,按式(16)进行变异概率取值操作:

设定一个代数计数器,每当遗传算法完成固定迭代次数后,进入模式搜索流程,进行局部寻优,将得到的局部最优值作为新个体放入遗传算法种群中,替换掉适应度最差的个体,继续进化。
模式搜索法初始化,将遗传算法得到适应度值最大的个体作为模式搜索的起始迭代点,即为:

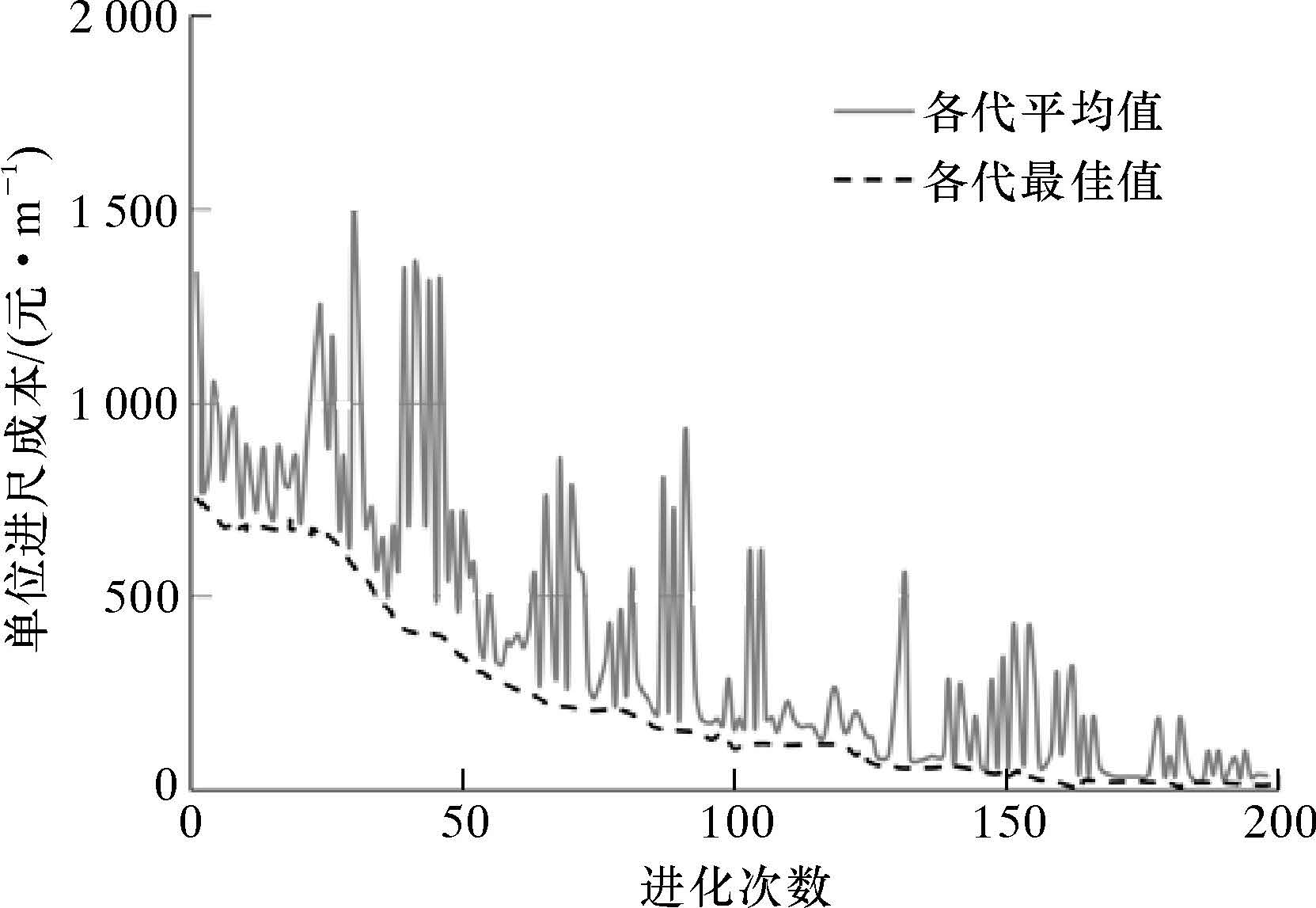
并设置初始步长为最终最优个体与最差个体差值的 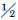 ,即为:
,即为:

在模式搜索迭代过程中,若步长缩小到低于收敛容限δtol,则终止搜索,输出此时的迭代点Rk,并将其编码为染色体个体通过替换放入遗传算法种群中继续进行进化迭代。
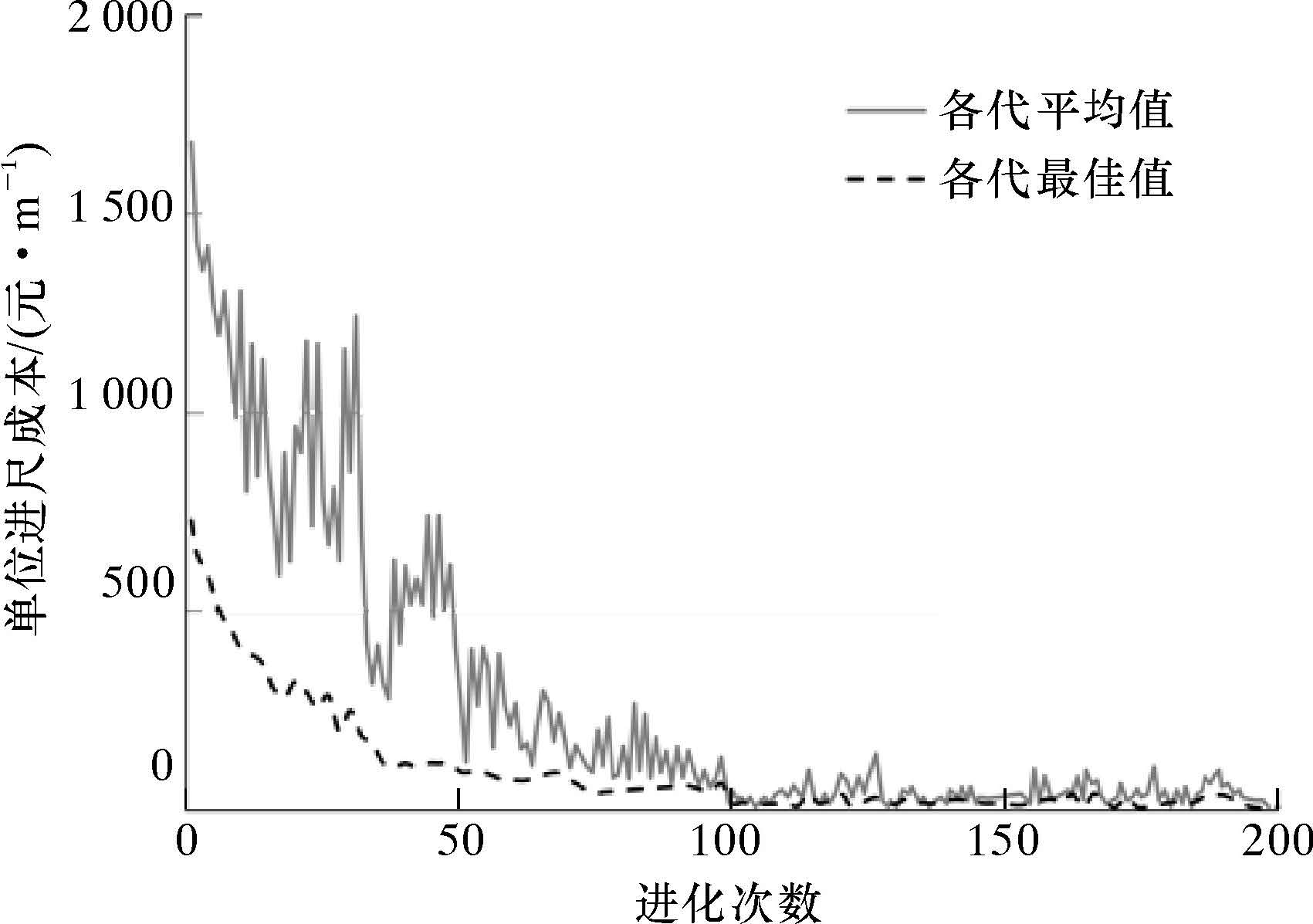
3 实例分析 3.1 仿真试验按照前文所建立的数学模型,针对具体井段的钻井参数组合,进行自适应遗传算法与模式搜索混合方法的仿真试验。以《钻井工程理论与技术》教材中的数据为例,某井段的地层可钻性系数K=0.002 3,研磨性系数Af=0.002 28,门限钻压M=10 kN,转速指数λ=0.68,采用直径为251 mm适合于中硬地层的21型钻头钻进该井段,查得钻压影响系数Z1=0.014 6、Z2=6.44,转速影响系数a1=1.5、a2=6.53×10-5,牙齿磨损减慢系数C1=5,牙齿磨损系数C2=3.68,钻头成本Cb=900元/只,钻机作业费Cr=250元/h,起下钻时间tt=5.75 h,可得出 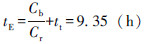 。
。
将上述各参数值代入目标函数式(7),分别选用模式搜索算法、自适应遗传算法以及笔者提出的基于模式搜索的改进遗传算法3种方法进行求解。遗传算法参数设置如下:种群规模100,进化次数200,初始交叉概率0.8,初始变异概率0.01。对迭代过程中的每代最优目标函数值和种群平均函数值进行记录,得到对比趋势曲线,如图 1所示。
|
| 图 1 模式搜索算法优化过程 Fig. 1 Pattern search algorithm optimization process |
图 1是只采用基本的模式搜索算法对问题优化,由图可知,模式搜索算法求解过程波动幅度较大,收敛过程相对缓慢,在进行150次迭代后,进化趋于最优解,但仍存在小幅波动现象。
图 2是自适应遗传算法优化过程,比模式搜索算法波动幅值衰减明显,求解过程相对平稳,在进行到约100次迭代的时候接近最优解,收敛速度比模式搜索算法有一定提升。
|
| 图 2 自适应遗传算法优化过程 Fig. 2 Adaptive genetic algorithm optimization process |
图 3是基于模式搜索的改进遗传算法对钻井参数组合的优化过程。从图可以看出,求解过程比前2种算法都更加稳定,波动幅度非常小,并且收敛速度得到显著提升,仅进行约70次种群进化后,就得到最大适应度值个体,即目标函数的最小值。综合以上分析可以得出,采用基于模式搜索的改进遗传算法求解钻井参数组合优选,可以获得更高的稳定性以及求解收敛速度。
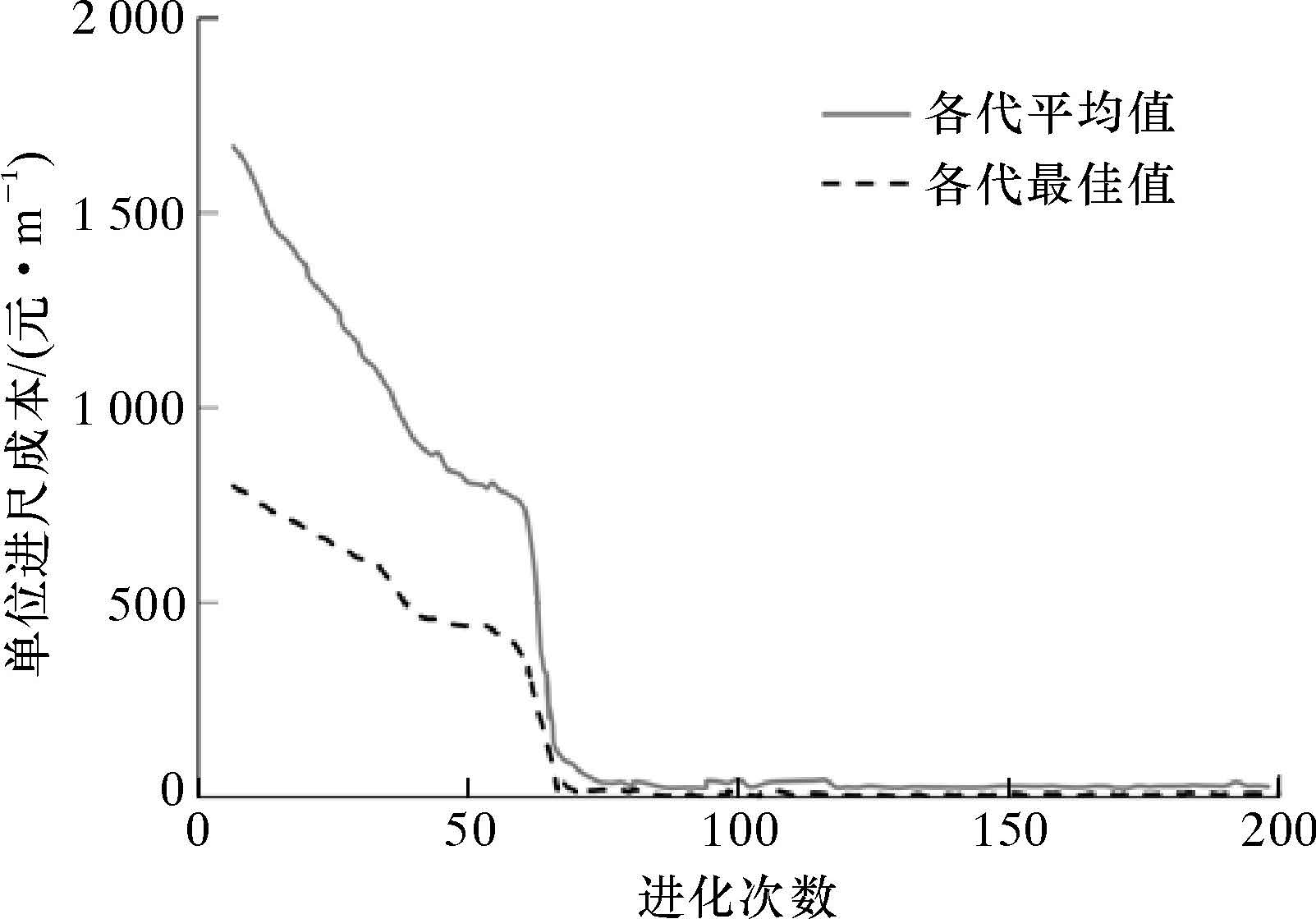
|
| 图 3 基于模式搜索的改进遗传算法优化过程 Fig. 3 Improved genetic algorithm optimization process based on pattern search |
在实例中所给条件下,用上述3种算法分别对目标函数进行求解,得到钻井参数优化组合数据如表 1所示。
| 方 法 | W/kN | n/(r·min-1) | hf | Cpm/(元·m-1) |
| 模式搜索 | 355 | 50 | 0.9 | 87.8 |
| 自适应遗传算法 | 340 | 78 | 1.0 | 80.5 |
| 混合算法 | 310 | 95 | 0.9 | 78.1 |
由表 1可以看出,基于模式搜索的改进遗传算法与自适应遗传算法和单一模式搜索算法得到的结果相近,其中模式搜索方法所得成本Cpm略高,说明模式搜索虽具有较强的局部寻优能力,但是全局寻优效果差,容易陷入局部最优,无法达到全局最优点。而基于模式搜索的改进遗传算法所得最终钻井米成本Cpm略低,用此算法可以完成钻井参数优化设计任务。
3.2 实例计算以克拉玛依某深井为例,该井3 864~4 158 m为二叠系上乌尔禾组,岩性以褐色、灰褐色泥岩与灰色砂砾岩为主,地层可钻性极值变化不大,研磨性系数取Af=2.5×10-3,设计用直径215.9 mm三牙轮钻头HJT517GK进行钻进,查得该钻头各项钻头参数为:钻压影响系数Z1=0.016,Z2=6.11,转速影响系数a1=0.5、a2=0.218×10-4,牙齿磨损减慢系数C1=2,钻头成本Cb=25 000元/只,钻井日费Cd=53 064元/d,可得钻井作业费Cr=2 211元/h。
由录井资料中选取该井段参与完全钻进的3个HJT517GK牙轮钻头,其钻进参数如表 2所示。
| 钻头编号 | 下入井深/m | 起出井深/m | 平均钻压/kN | 平均转速/(r·min-1) | 钻头磨损量 |
| 6 | 3 864.00 | 3 942.16 | 150 | 75 | 0.6 |
| 9B | 3 972.63 | 4 009.06 | 175 | 56 | 0.7 |
| 9C | 4 013.28 | 4 067.04 | 171 | 64 | 0.6 |
在确定了上述各系数以及约束条件后,用基于模式搜索的改进遗传算法对各钻头工作井段钻井参数进行优化,求取最优钻压、最优转速以及最优钻头磨损量,得到结果如表 3所示。
| 编号 | K | λ | M/kN | C2 | tt/h | Wopt/kN | nopt/(r·min-1) | hf | Cpm/(元·m-1) | Cpma/(元·m-1) |
| 6 | 0.002 4 | 0.58 | 60 | 1.69 | 43.9 | 170 | 55 | 0.8 | 2 620.2 | 3 255.6 |
| 9B | 0.002 6 | 0.54 | 55 | 1.53 | 52.3 | 180 | 51 | 0.9 | 2 523.9 | 3 405.5 |
| 9C | 0.001 5 | 0.40 | 70 | 1.76 | 14.6 | 190 | 63 | 0.94 | 5 763.3 | 7 525.6 |
表 3中,Wopt为最优钻压,nopt为最优转速,Cpm为优化后钻井成本,Cpma为实际钻井成本。
由表 3可以看出,优化钻压比实际钻压平均值略高,在该地层推荐采用高钻压进行钻进;而优化转速与实际钻速平均值相差不大;优化钻头磨损量比实际使用钻头磨损量大,若在钻头磨损量达到0.8~0.9时再起出钻头,则可提高钻头使用率,能够在一定程度上降低钻井米成本,提高钻井经济效益。
4 结 论(1)为改善自适应遗传算法局部寻优精度较差的缺陷,提出了基于模式搜索的遗传混合算法。
(2)在自适应遗传算法解决非线性规划问题的基础上,对每代种群进行模式搜索,使得该混合算法既具有较强的全局搜索能力,又提高了局部寻优精度。
(3)笔者确定了钻井参数优选的目标函数以及约束条件,并以克拉玛依油田已钻井数据对算法进行验证,结果说明该算法提高了迭代收敛的稳定性以及迭代收敛速度,提高了数据分析结果的可靠性。
(4)若基于区域三维地层岩石参数数据体[9],该优选方法可用于钻前钻井参数优选,为制定钻井设计方案提供依据。
| [1] | 刘杨,张书瑞,崔已男,等.基于随机钻井模式的钻井参数优化方法[J].石油钻采工艺,1994,16(1):38-43. |
| [2] | 王江萍,孟祥芹,鲍泽富.钻进参数实时监测与故障诊断技术[J].钻采工艺,2008,31(1):49-52. |
| [3] | 张厚美,王棠青.动态法优选钻井参数[J].石油钻采工艺,1992,14(1):13-18,36. |
| [4] | 张立刚,吕华恩,李士斌,等.钻井参数实时优选方法的研究与应用[J].石油机械,2009,37(4):35-37. |
| [5] | 伊鹏,刘衍聪,郭欣,等.基于改进自适应遗传算法的钻井参数优化设计[J].石油机械,2010,38(2):30-33. |
| [6] | 葛培明.改进的遗传算法及其在工程优化中的应用[D].成都:西南交通大学,2006. |
| [7] | 王小平,曹立明.遗传算法:理论,应用及软件实现[M].西安:西安交通大学出版社,2002. |
| [8] | 吴兴远.模式搜索法在最优化问题中的应用[J].软件导刊,2009 (8):122-123. |
| [9] | 耿智,樊洪海,陈勉,等.区域三维空间岩石可钻性预测方法研究与应用[J].石油机械,2014(5):80-84. |



