2. 中国石油大学(华东)储运与建筑工程学院
2. College of Pipeline and Civil Engineering, China University of Petroleum(Huadong)
0 引 言
我国地质灾害多发,新粤浙管道穿越新疆、甘肃宁夏、华北和华南4个不同地区时,不可避免地会穿越强震区和活动断层区等典型地质灾害区,易导致管道产生过量变形而失效破坏,造成重大的经济损失和人员伤亡。因此,对于穿越活动断层的埋地管道进行安全可靠性研究至关重要。
冯启民和赵林等[1, 2]将埋地管道简化成4节点的薄壳单元,将场地土简化成弹塑性弹簧,考虑了两者的材料非线性,分析了径厚比、断层运动形式、倾角、土体刚度和内压等参数的影响。梁瑞等[3]根据数学模型建立了地震波载荷作用下梁-土弹簧有限元分析模型,研究了埋地管道在某一Ⅶ级地震载荷作用下的位移响应。郝婷玥等[4]采用时程分析方法对管-土-流体模型进行研究,分析了地震动参数和场地条件等因素对埋地管道响应的影响规律。
由此可见,前人对地震载荷作用下埋地管道的分析主要针对地震波或者断层单独作用下管道的应力响应。然而,对于地震等位移形式载荷的作用,当埋地管道开始出现塑性变形时,管道虽然依旧可以满足安全生产的正常要求,但是由于此时管内应力超出管材的屈服极限,基于应力的设计准则就不再适用[5, 6],而采用应变作为标准,可以更方便有效地衡量和控制管道的极限状态。为此,笔者采用基于应变的方法研究地震波作用下穿越断层埋地管道的变形情况,讨论地震烈度、断层错距、管径、壁厚、埋深和土壤内摩擦角等因素对管道安全的影响,以期为地震波作用下穿越活动断层区的长输管道的可靠性设计提供依据。
1 埋地管道有限元模型及可靠性分析 1.1 有限元分析模型考虑埋地管道和场地土的材料非线性与几何非线性,采用4节点薄壳单元建立长输管道模型,用非线性弹簧单元模拟管土相互作用。壳单元任意节点均与管轴方向、水平横向和垂直方向土弹簧连接。采用加速度时程的方法输入地震波,并在每个土弹簧的节点加上活动断层相应方向上的位移分量,用以模拟管道受到的断层作用。
首先利用ANSYS中的概率设计模块,获得各随机输入变量对地震载荷作用下穿越活动断层的长输管线的可靠度的影响程度。在此基础上,深入研究影响显著的因素对地震波和断层位移双重作用下埋地管道变形情况的影响规律。管-土有限元分析模型如图 1所示。

|
| 图 1 埋地管道有限元模型 Fig.1 Finite element model of buried pipeline |
埋地管道管径1.219 m,壁厚26.4 mm,弹性模量206 GPa,泊松比0.3,设计压力12 MPa。长输管线管材选用X80钢。假设场地土为中硬土,埋深2.1 m,土壤内摩擦角35°,土壤容重1.8×104 N/m3。管道与断层交角为90°,断层错距0.7 m,断层倾角70°,地震烈度为Ⅷ度。
1.2 模型计算结果可靠性验证目前,计算埋地管道轴向最大应变的方法中,经典的有拟静力分析法和Newmark-Hall法[7, 8, 9]。拟静力分析法的核心思想是将地震波作用简化为一个惯性力,从而在静力分析的基础上展开进一步研究。拟静力分析法考虑了管土相互作用,对于地震评价报告已经给出地震系数,在项目组织实施之前预测某地区埋地管道的震害情况较为合适。Newmark-Hall法由于忽略了场地土对管道的横向作用和管道内的弯曲变形,假设埋地管道只受轴向滑动摩擦力作用,所以其计算结果偏小。
为验证有限元分析模型计算结果的可靠性,选取新粤浙管道穿越某一断裂带的基本数据,对比分析2种理论分析法和有限元法的计算结果。不同计算方法所得埋地管道轴向最大应变如表 1所示。
| 单一因素 | 地震波 | 活动断层 | ||
| 拟静力分析法 | 有限元法 | N-H法 | 有限元法 | |
| 计算结果/% | 0.017 | 0.016 | 0.120 | 0.140 |
由表 1可见,对于埋地管道在地震波作用下的轴向最大应变,拟静力分析法与有限元法计算结果的相对误差为5.9%,小于8%,满足工程需要。对于埋地管道在活动断层作用下的轴向最大应变,有限元法的计算结果比Newmark-Hall方法的结果略高(16.7%)而由于后者计算结果偏小,从而说明有限元法的计算精度更高。综上,笔者所建管土相互作用模型的计算结果具有可靠性。
1.3 应用蒙特卡罗法分析管道的可靠性长输管道在设计、施工和运输过程中存在各种不确定性,例如对管土相互作用模型进行计算时,必然要引入载荷参数、几何参数和力学参数等基本变量。但是由于存在测量误差等各种不确定性,导致这些变量的取值只能通过随机变量来表示。穿越断层埋地管道可靠性分析实际上是综合运用弹塑性力学理论和概率分析方法,首先对管道刚度特性起主要影响作用的随机变量进行抽样,其次对管道进行随机响应分析,并对结构响应进行概率统计分析,进而求得穿越断层埋地管道的可靠度。
利用ANSYS中的概率设计模块,建立了多随机因素作用下的穿越断层埋地管道可靠度模拟方法,给出了所涉随机变量的均值和分布类型。随机变量包括内压、管道外径、管道壁厚、埋深、错距、管道泊松比及地震动峰值加速度。随机变量均为正态分布,平均值为:内压12 MPa,管道外径1.219 m,壁厚26.4 mm,埋深2.1 m,错距0.7 m,管道泊松比0.3,地震动峰值加速度2 m/s2。
埋地管道在正常运行过程中,判断其是否失效的依据是管道轴向最大应变是否超过容许应变,因此建立极限状态函数DETSS=g(x1,x2,……,xk)=εmax-[ε]F,当DETSS>0时,管道处于可靠状态;当DETSS=0时,管道处于极限状态;当DETSS<0时,管道失效。由循环1 000次的分析结果得出,当设置置信水平为95%时,X80(1.219 m×26.4 mm)埋地钢质管道在12 MPa的设计压力下的失效概率为0,即可靠度为100%。
管道轴向最大拉伸应变灵敏度如图 2所示。根据灵敏性分析结果,可以判断各随机变量对DETSS的影响比重,对影响显著的因素在管道抗震设计阶段进行优化,缩小它们的波动范围,可以提高管道的可靠度,进而在满足可靠度要求的前提下降低成本。

|
| 图 2 管道轴向最大拉伸应变灵敏度图 Fig.2 Sensitivity map of the pipeline maximum axial tension strain |
由图 2a可以看出,地震烈度、埋深、管径、土壤内摩擦角、错距和壁厚为管道轴向最大拉伸应变的显著影响因素,而设计压力的影响程度相对较小。其中,地震烈度、埋深、土壤内摩擦角以及活动断层的错距等与轴向最大拉伸应变呈正相关关系,管道的壁厚、外径与轴向最大拉伸应变呈负相关关系。
由图 2b可以看出,容许拉伸应变是极限状态函数DETSS的最显著影响因素,地震烈度、埋深和壁厚的影响程度依次递减。其中,地震烈度、埋深与DETSS呈负相关关系,即地震烈度或者管道埋深越大,埋地管道的可靠度越小。管道的壁厚与DETSS呈正相关关系,即壁厚越大,管道的可靠度越大。
通过分析各因素对管道可靠度的影响程度及自身可控程度,以及结合现场实际情况,要提高埋地管道的可靠度,依次需要考虑的因素是埋深、壁厚和穿越活动断层的位置。其中,埋深方面要尽量降低管土相互作用,浅埋虽然有利于管道的抗震,在实际施工过程中还需综合考虑便于维修等因素;壁厚方面,理论上应选择大口径的厚壁钢管,但要在满足可靠度要求和安全运行的前提下降低成本,应适当减小壁厚和管径;穿越活动断层的位置方面,应根据资料与现场情况,选择活动断层错动位移量较小的位置。
2 影响埋地管道轴向应变的因素及程度 2.1 地震烈度的影响地震烈度对埋地管道轴向最大应变的影响如图 3所示。从图可以看出,随着地震烈度的不断增大,穿越断层埋地管道的轴向最大拉伸应变和轴向最大压缩应变均逐渐增大。当地震烈度为Ⅱ度、断层错距为0.7 m时,管道穿越强震区轴向最大拉伸应变值为2.28%,超过了容许拉伸应变。当地震烈度从10度增加到12度,管道轴向最大拉伸应变和最大压缩应变分别增加了24.1%和23.1%。

|
| 图 3 地震烈度对埋地管道轴向最大应变的影响 Fig.3 The impact of seismic intensity on pipeline maximum axial strain |
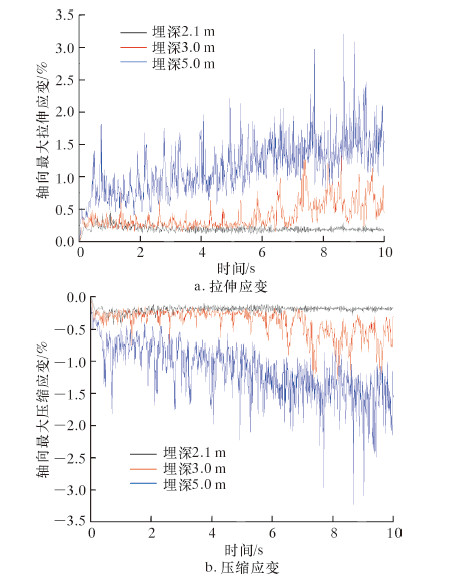
埋深对埋地管道轴向最大应变的影响如图 4所示。
|
| 图 4 埋深对埋地管道轴向最大应变的影响 Fig.4 The impact of buried depth on pipeline maximum axial strain |
从图可以看出,在断层错距不变的情况下,当管道埋深增加时,穿越断层埋地管道轴向最大拉伸应变和轴向最大压缩应变均逐渐增大。当断层错距为0.7 m时,管道埋深从2.1 m增加到3.0 m,管道轴向最大拉伸应变和最大压缩应变分别增加了201.0%和117.6%。
由此可见,埋深对埋地管道轴向应变的影响十分显著。随着埋深的增加,由于管轴方向土壤摩擦力、水平横向和垂直方向的土壤反力逐渐增加,场地土对埋地管道的约束程度不断增加。对于埋深不超过的5 m的管道而言,当埋深逐渐增加时,管道轴向最大拉伸应变及轴向最大压缩应变都越大,管道越容易发生破坏。同时,管道埋深越浅则地面波传递的能量越小,管道的破坏率也越小。因此,对管道进行浅埋既可以减轻震害造成的损失,也有利于施工维修。
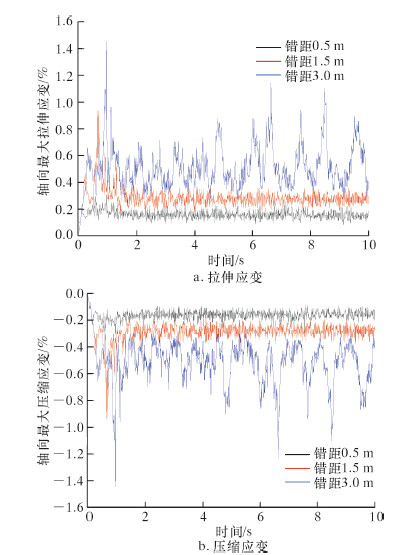
2.3 错距的影响错距对埋地管道轴向最大应变的影响如图 5所示。
|
| 图 5 错距对埋地管道轴向最大应变的影响 Fig.5 The impact of fault offset on pipeline maximum axial strain |
从图 5可以看出,随着活动断层位移错动量的增加,埋地管道的轴向应变逐渐增大。断层错距从0.5 m增加到1.5 m时,管道轴向最大拉伸应变和最大压缩应变分别增加了205.3%和208.0%。因此,为满足管道设计应变的要求,应考虑调整管道的几何尺寸和性能参数等方案。
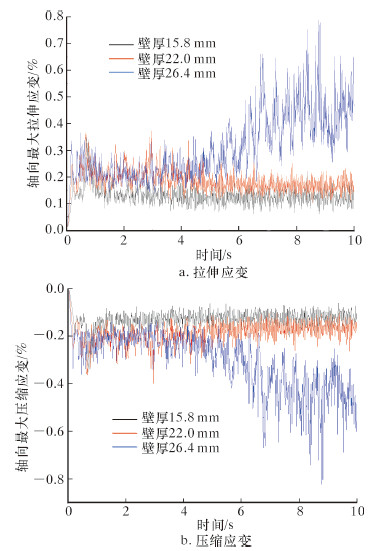
2.4 壁厚的影响壁厚对埋地管道轴向最大应变的影响如图 6所示。从图可以看出,在相同断层错距的作用下,随着壁厚的减小,埋地管道的轴向最大拉伸应变和轴向最大压缩应变都逐渐增大。当错距为0.7 m时,随着壁厚从26.4 mm减小到22.0 mm,管道轴向最大拉伸应变和最大压缩应变分别增加了5.7%和14.3%。这是因为随着壁厚的减小,管道内、外径之比增大,横截面的惯性矩减小,从而导致管道应变增大。而且薄壁钢管容易产生屈曲破坏和塑形应变集中的现象,因此对于埋地管道的抗震设计而言,选择厚壁钢管更加安全。
|
| 图 6 壁厚对埋地管道轴向最大应变的影响 Fig.6 The impact of wall thickness on pipeline maximum axial strain |
(1)地震烈度是影响埋地管道可靠度最为显著的因素,其次是埋深和壁厚。随着地震烈度的增加,埋地管道震害率增加。当地震烈度为Ⅱ度、断层错距为0.7 m时,管道穿越强震区轴向最大拉伸应变值为2.28%,超过了容许拉伸应变,易发生失效破坏。
(2)埋深、土壤内摩擦角、活动断层错距与轴向最大拉伸应变呈正相关关系,管径、壁厚与轴向最大拉伸应变呈负相关关系。
(3)建议现场设计施工时尽量避开大位错活动断层带,选择大口径、厚壁钢管并浅埋在土壤相对密实的区域。
| [1] | 冯启民,赵林.跨断层埋地管道屈曲分析[J].地震工程与工程振动,2001,21(4):81-87. |
| [2] | 赵林,冯启民.埋地管线有限元建模方法研究[J].地震工程与工程振动,2001,21(2):53-57. |
| [3] | 梁瑞,马东方,俞树荣,等.埋地管道在地震载荷作用下的动力响应分析[J].石油机械,2007,35(12):16-18. |
| [4] | 郝婷玥,陈贵清,马卫华.地震作用下埋地管道横向振动分析[J].四川建筑科学研究,2010,36(2):204-207. |
| [5] | 余志峰,史航,佟雷,等.基于应变设计方法在西气东输二线的应用[J].油气储运,2010,29(2):143-147. |
| [6] | 刘冰,刘学杰,张宏.基于应变的管道设计准则[J].天然气工业,2008,28(2):129-131. |
| [7] | 朱秀星.地质灾害环境下埋地油气管线安全性研究[D].青岛:中国石油大学(华东),2009. |
| [8] | 姜华.埋地管道在地震波作用下的响应分析[D].武汉:华中科技大学,2011. |
| [9] | 中国石油天然气股份有限公司管道建设项目经理部.Q/SY GJX 0136-2008西气东输二线管道工程强震区和活动断层区埋地管道基于应变设计导则[S].北京:石油工业出版社,2008. |



