0 引 言
穿越活动断层管道的安全性是管道建设重点关注的问题,通常采用基于应变的方法进行抗震设计校核[1, 2, 3, 4],而使用有限元方法进行管道设计时,应变计算则是其设计基础。有限元模型考虑管材、管土作用及大变形等多重非线性,能够较准确地描述管道在断层作用下的应力-应变响应。现有的有限元模型包括(梁)管单元模型[5, 6, 7, 8, 9]与壳单元模型,其中壳单元模型又分为固定边界、管(梁)-壳耦合[10, 11]和等效弹簧边界[12, 13]。近年来使用实体单元模拟土壤,部分学者使用以非线性接触描述管土相互作用的有限元模型[14, 15]。
刘爱文等[12]提出等效边界模型后,对比了固定边界与等效边界模型;Xie Xiaojian等[16]对比了基于管单元与壳单元在走滑断层作用下HDPE管道的应变响应,结果表明两者比较相近。笔者基于ABAQUS分别建立4种断层作用下管道应变计算有限元模型,使用实际工作载荷参数并考虑多种工况,从计算结果的差异性与计算效率2方面对比4种模型的优缺点,给出模型的适用范围,以期对工程应用起到一定的指导作用。
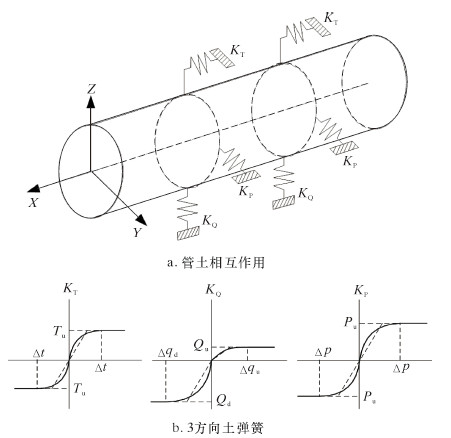
1 有限元模型 1.1 管土相互作用模型管土相互作用是复杂的非线性问题,土弹簧将管土之间作用离散为3个方向具有不同刚度的弹簧:轴向刚度KT、垂向刚度KQ和水平向刚度KP,如图 1a所示;土弹簧刚度可近似由管土极限作用力和屈服位移确定的折线表示,如图 1b所示,其数值大小可由文献[2]中公式求得。
|
| 图 1 土弹簧作用示意图 Fig.1 Schematic of soil spring |
管土之间利用Jointc单元连接并模拟土弹簧的作用。Jointc单元可以描述2个节点之间随相对位移变化产生的相互作用力。
1.2 管道模型 1.2.1 管单元ABAQUS中梁属管单元包括Pipe管单元和Elbow弯管单元:Pipe管单元截面环向有4个积分点,对应管顶、管底和管两侧;Elbow弯管单元是ABAQUS软件提供的一种类壳单元,具有壳单元的复杂变形特点,在管截面使用全壳积分,环向默认20个积分点,可以描述管道在三维空间中变形后截面椭圆化或管道翘曲等行为。Elbow弯管单元比普通梁单元计算成本偏高,但是低于壳单元。管单元模型使用Elbow31弯管单元模拟。
1.2.2 壳单元壳单元结构一个方向尺度远小于其他方向,并忽略厚度方向应力。针对大口径薄壁管道,将其离散成若干矩形壳单元,可准确描述管道在力或位移载荷作用下的变形与应力应变分布,同时壳单元可以描述管道的局部屈曲行为。壳单元模型使用ABAQUS中的线性、有限薄膜应变、完全积分的四边形壳单元S4,能够准确求解平面弯曲问题。
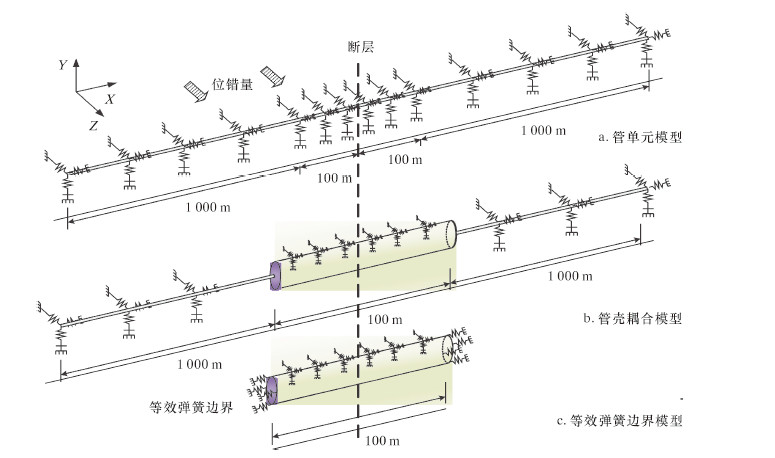
1.3 管道穿越断层有限元模型建立 1.3.1 管单元模型模型如图 2a所示,采用Elbow31单元模拟管道,Jointc单元模拟土弹簧;断层两端各100 m范围管道每0.1 m间隔1个单元,较密单元用来更准确描述管道变形,加密段两侧各1 000 m内每1 m间隔一个单元,用来描述管道远端行为。
|
| 图 2 管道穿越断层有限元模型 Fig.2 Finite element model of pipeline crossing fault |
使用壳单元模拟管道,管道分析长度2 000 m足以消除边界影响;管道沿轴向每0.4 m划分1个单元,沿环向分割24个单元;每个管道节点对应1个土节点,以Jointc单元连接模拟3个方向土弹簧。
1.3.3 管壳耦合模型模型如图 2b所示,穿越断层附近100 m内管道采用壳单元建模,管道环向24个单元,在轴向每0.4 m长度1个单元;两端采用管单元建模,长度分别取1 000 m。壳单元管道两端与管单元管道耦合,将管单元管道端部作为控制点,约束壳单元管道端部区域的全部6个自由度,此区域的各节点之间不会发生相对位移,只会随着控制点做刚性运动,即将管端行为传递给壳单元管道边界,因此缩减了单元数量,降低了计算成本。
1.3.4 等效弹簧边界模型远离断层的管土小变形段可以用非线性等效弹簧来模拟,从而代替距断层较远处直线段管道的变形影响。模型如图 2c所示,壳单元管道模型长度100 m,环向24个单元,轴向每0.4 m长度1个单元;两端连接24个弹簧单元用以描述等效弹簧。
等效弹簧外力F与伸长量ΔL之间关系为[12]:
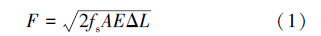
该公式假设远端管道处于弹性状态,只受到均匀分布滑动摩擦力,忽略静摩擦力影响。
2 案例分析与结果对比 2.1 管材参数采用Ramberg-Osgood模型来描述管材的弹塑性模型。该模型能对屈服应变4%以下的管材应力应变关系进行较好的拟合,适用于管道应变求解,应力-应变关系表达式如下:
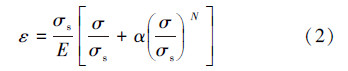
有限元模型选用我国西气东输二线断层区敷设X80HD2管道,其基本参数为:外径1 219 mm,壁厚22 mm,在Ramberg-Osgood模型中α=15.94,N=15.95。
2.2 土弹簧参数断层区管道敷设管沟采用砂土回填,砂土内摩擦角35°,管土摩擦因数0.6,土壤容重力18 kN/m3;管径1 219 mm,埋深1.8 m。根据文献[2]中公式计算得到土弹簧参数,如表 1所示。
| 方 向 | 极限抗力/(kN·m-1) | 位移/mm |
| 轴向弹簧 | 40 | 3 |
| 侧向弹簧 | 430 | 96 |
| 垂直向上 | 52 | 27 |
| 垂直向下 | 2 360 | 122 |
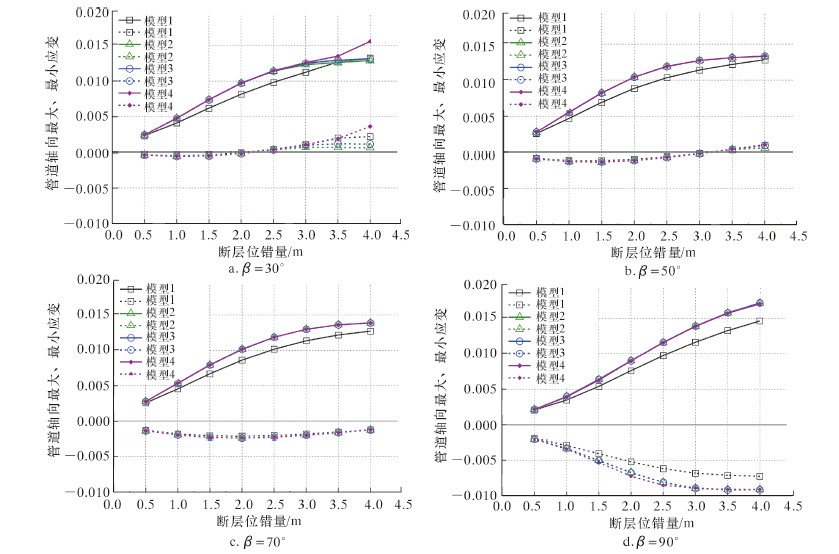
根据不同算例计算结果和计算成本研究有限元模型之间的差异。当管道穿越走滑断层时,管道与断层交角β分别取30°、50°、70°和90°,走滑断层水平位错量分别取0.5、1.0、1.5、2.0、2.5、3.0、3.5和4.0 m;提取管道以断层为中心两侧各50 m内的轴向最大应变和最小应变,结果如图 3所示。
|
| 图 3 不同算例下管道轴向应变对比 Fig.3 The pipeline axial strain under different calculation examples |
由图 3可知,管单元模型计算所得轴向最大应变略小于壳单元模型,当穿越角为30°~70°时轴向最小应变与壳单元模型相当,当穿越角为90°时略小于壳单元模型;使用管壳耦合或等效弹簧边界来模拟远端管道,计算结果与2 000 m固定边界壳单元模型较接近,其中穿越角30°、位错量3.0 m以上时采用等效弹簧边界模型计算得到的应变值偏大。
图 3中,模型1为管单元模型、2为固定边界壳单元模型、3为管壳耦合模型、4为等效弹簧边界模型;实线为最大应变,虚线为最小应变。
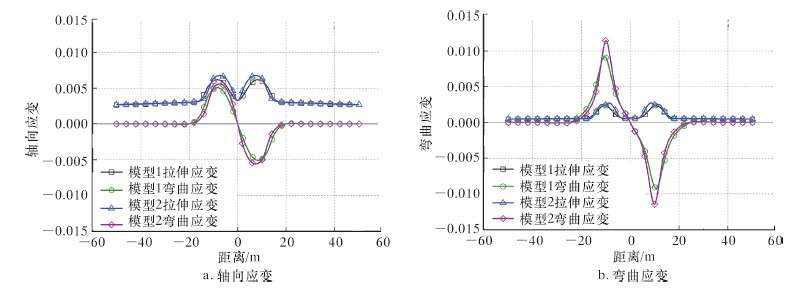
分别提取管单元模型和固定边界壳单元模型穿越角30°和90°,断层位错量3 m时断层附近100 m范围管道轴向应变与弯曲应变(见图 4)。当穿越角为30°时,管单元模型与壳单元模型轴向应变与弯曲应变较接近;当穿越角为90°时,模型之间轴向应变较接近,但基于壳单元模型管道弯曲应变较大,导致计算所得轴向最大应变和最小应变均偏大。
|
| 图 4 轴向应变与弯曲应变对比 Fig.4 The axial strain and bending strain of the pipeline |
等效弹簧边界本质是断层发生错动管土之间相互作用时,将远离断层管道(两端各50 m外)所受土壤外力与伸长量之间非线性关系用弹簧表示并加载,公式推导基于远端管道全部处于线弹性阶段。当穿越角为30°、位错量为4 m时,100 m范围内管道最小轴向应变为正,管道全部处于拉伸状态,此时壳单元两端应力为534.50 MPa,大于管道屈服强度,仍处于塑性变形状态,即远端管道并不全部处于线弹性阶段。由此可知,如果仍以远端管道线弹性计算得到非线性弹簧刚度将比真实值偏大,导致计算结果偏大[12]。将模型中壳单元管道长度由100 m增加至150 m,同算例下计算得到轴向最大应变和最小应变分别为1.47%与0.25%,与固定边界壳单元模型相符。
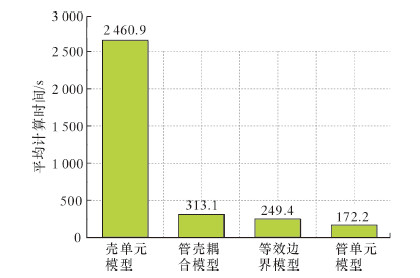
使用壳单元模拟管道在断层作用下的变形时,常采用管壳耦合或者等效弹簧边界的手段来控制计算成本。其基本思想均是通过将远离断层管土作用简化来减少单元数,控制刚度矩阵,缩减计算成本。通过算例下平均计算时间来衡量模型计算成本,计算机主频2.60 GHz,内存32 Gb,计算时占用CPU16个,结果如图 5所示。从图可见,管壳耦合模型和等效弹簧边界模型均大幅缩短了计算时间,与管单元模型相比,后者经济性更高。
|
| 图 5 不同模型平均计算时间对比 Fig.5 The average computation time of different models |
(1)对管道以不同角度穿越不同位错量走滑断层时最大与最小轴向应变进行比较可知,弯管单元模型、壳单元管道模型、管壳耦合模型和等效弹簧边界模型结果较接近,其中基于壳单元模型计算结果稍保守。
(2)在保证计算结果准确性的前提下,采用管壳耦合模型或等效弹簧边界模型可大幅缩减计算成本,后者在特殊情况(断层位错量较大)下需加长管段分析长度,以保证等效弹簧边界适用性。
(3)管单元模型具有最优计算效率,适合大批量计算时使用;管壳耦合模型具有较高计算效率、较广适用性以及较保守的计算结果,适合断层区管道抗震设计时使用。
| [1] | CSA Z662-2007 Oil and gas pipeline systems[S].2007. |
| [2] | American lifelines alliance.Guideline for the design of buried steel pipeline[S].2001. |
| [3] | GB 50470-2008油气输送管道线路工程抗震技术规范[S].2008. |
| [4] | 张宏,崔红升.基于应变的管道强度设计方法的适用性[J].油气储运, 2012, 31(12):952-954. |
| [5] | Tohidi R Z.Shakib H.Response of steel buried pipeline to the three-dimensional fault movements[J].Journal of Science and Technology, 2003, 14:1127-1135. |
| [6] | Joshi S, Prashant A, Deb A, et al.Analysis of buried pipelines subjected to reverse fault motion[J].Soil Dynamics & Earthquake Engineering, 2011, 31(7):930-940. |
| [7] | 刘学杰,孙绍平.地下管道穿越断层的应变设计方法[J].特种结构, 2005, 22(2):81-85. |
| [8] | 刘啸奔,陈严飞,张宏,等.跨断层区X80钢管道受压时的设计应变预测[J].天然气工业, 2014, 34(12):123-130. |
| [9] | Liu Xiaoben, Zhang Hong, Chen Yanfei.Strain prediction of X80 steel pipeline at strike-slip fault under compression combined with bending[C]//Proceedings of the 2015 ASME Pressure Vessels & Piping Conference, July 19-23, 2015, Boston, USA. |
| [10] | Takada S, Hassani N, Fukuda K.A new proposal for simplified design of buried steel pipes crossing active faults[J].Earthquake Engineering & Structural Dynamics, 2001, 30(8):1243-1257. |
| [11] | Liu M, Wang Y Y, Yu Z F.Response of pipelines un-der fault crossing[C]//Proceedings of the Internat-ional Offshore and Polar Engineering Conference.Vanc-ouver:ISOPE, 2008. |
| [12] | 刘爱文,胡聿贤,赵凤新,等.地震断层作用下埋地管线壳有限元分析的等效边界方法[J].地震学报, 2004, 26(增刊1):141-147. |
| [13] | 闫相祯,张立松,杨秀娟.管道穿越地震断层管土耦合大变形壳模型的应变响应规律研究[J].土木工程学报, 2010(8):132-139. |
| [14] | Vazouras P, Karamanos S A, Dakoulas P.Finite element analysis of buried steel pipelines under strike-slip fault displacements[J].Soil Dynamics & Earthquake Engineering, 2010, 30(11):1361-1376. |
| [15] | Trifonov O V, Cherniy V P.A semi-analytical approa-ch to a nonlinear stress-strain analysis of buried steel pipelines crossing active faults[J].Soil Dynamics & Earthquake Engineering, 2010, 30(11):1298-1308. |
| [16] | Xie Xiaojian, Symans M D, O'Rourke M J, et al. Numerical modeling of buried hdpe pipelines subjected to strike-slip faulting[J].Journal of Earthquake Engineering, 2011, 15(8):1273-1296. |



