2. 四川川庆石油钻采科技有限公司
2. Sichuan Chuanqing Petroleum Drilling & Production Technology Co., Ltd
0 引言
油气井的生产周期往往由石油套管的服役寿命决定,而套管和接箍间螺纹接头的损坏是造成套管失效的最主要因素,也是套管结构中最薄弱的环节。随着复杂结构井和热采井的大量应用,以及储层改造的需要,温度场和应力场会发生改变,特别是稠油热采井的蒸汽温度会达到300 ℃以上,这些都会导致套管螺纹接头面临多种不同工况,直接影响接头的可靠性。
偏梯形螺纹相比于圆形螺纹不易产生滑扣,因此在许多苛刻的井身结构中被广泛采用[1]。国内学者对套管螺纹接头的研究主要集中在圆形螺纹,主要结论包括不同过盈圈数下扣牙应力和压力分布规律以及改善应力分布的措施等[2, 3]。现有的研究方法主要包括试验解析法、测定法、数值计算法以及这几种方法的结合[4]。有限元方法是研究该问题最常用的方法,计算模型一般采用轴对称模型进行简化,研究成果集中在螺纹结构的既有参数优化以及特殊接头螺纹的性能评价[5, 6, 7]。祝效华等[8, 9]采用 1/2 尺寸模型来分析拉弯复合载荷作用下的短圆套管螺纹应力分布规律,采用全尺寸模型分析了磨损套管连接螺纹的三维力学行为,得到了不同井眼曲率下的周向接触压力分布。王树平等[10]研究了热应力对套管接头接触压力的影响,总结了不同温度载荷下的接触压力变化规律。见诸于这些文献中的套管螺纹接头研究,一般都很少关注温度场的影响。为此,笔者分析了不同工况条件下温度-应力场对套管螺纹接头的结构影响。
1 力学模型及计算方程温度-应力耦合模型所涉及的理论公式包括Von Mises 屈服准则、Prandtl-Reuss理论、热弹性位移势和收缩配合圆筒理论等。对于模型的弹性变形区采用Hook定理进行描述,对于塑性变形区采用材料力学中的第四强度理论,即Mises屈服准则进行描述。套管接头一般可视为均质金属,其平面应变过程可用Prandtl-Reuss理论进行描述,由此推导出理想弹塑性材料的增量本构方程如下。

计算模型是平面应变问题,如果采用位移法求解,则位移分量、应变分量和应力分量都可用热弹性位移势来表,其温度应力的表达式为:

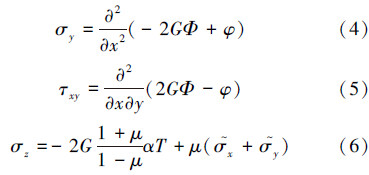
将位移势Φ和Airy应力函数φ代入式(3)~式(6)计算可得到各个温度应力分量。
螺纹过盈连接的应力计算可采用Lame应力公式和收缩配合圆筒理论作为基础[2]。Lame方程需要将问题建立在极坐标系中,最终得到套管接头受内、外压共同作用下的弹性应力和位移解。
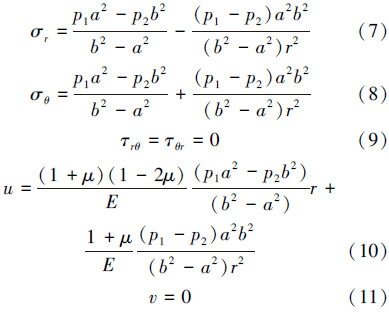
结合弹塑性力学以及弹塑性有限元理论,利用ABAQUS软件强大的系统级多物理场分析能力,对采用偏梯形螺纹接头的P110(298.45 mm×11.43 mm)套管进行不同工况下的温度-应力耦合分析。套管接头的具体结构尺寸参见API SPEC 5B标准[11]。P110套管的材料特性为:弹性模量201 GPa,泊松比0.3,热膨胀系数1.2×10-5 m/℃,导热系数48.36 W/(m·℃)。
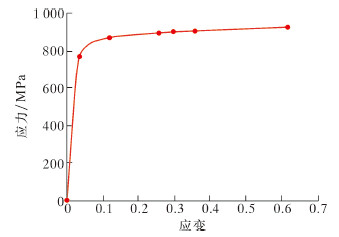
模型中用到的P110套管的真实应力-应变数据所绘制的曲线如图1所示,是通过单向拉伸/压缩试验中得到的名义应变和名义应力换算得到。在进行材料参数设置时,还考虑了温度T对套管弹性模量Et以及膨胀系数β的影响,其换算公式如下:
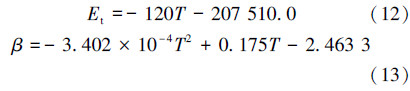
|
| 图 1 P110套管应力-应变曲线 Fig.1 The stress-strain curve of P110 casing |
为了提高计算效率和计算精度,现做出以下假设和处理:
(1)所研究型号的套管接头螺纹升角很小,对载荷分布的影响可以忽略,可将接头简化为轴对称结构;
(2)模型材料的非线性程度较小,对分析结果的影响也较小,视为均匀的各向同性体;
(3)考虑圣维南原理,建立了合理的套管管体长度,以保证位移边界和轴向施加位置能消除圣维南效应对应力敏感区的影响。
选用CAX4T单元和进阶算法来对部件进行网格单元划分。为了得到合理的网格分布以及准确的计算结果,不仅在螺纹接触对位置对网格进行了局部加密,还对每个螺纹牙齿前端进行了剖分,且沿剖分线进行了单向偏置布种。最终得到套管单元数12 484个,节点数13 067个,接头单元数13 377个,节点数14 029个。螺纹间的接触公式采用带库伦摩擦属性的小滑移公式。根据API标准,扭矩可以转化为轴对称模型中的轴向拉应力,预紧力可以通过过盈配合等效。在不同工况下施加不同的边界条件和载荷,但是套管接头的内压和外压保持不变,图2为受拉状态下的套管接头有限元模型。
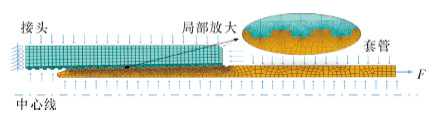
|
| 图 2 受拉状态下套管接头有限元模型 Fig.2 Finite element model of the casing joint under tension state |
套管螺纹接头承受拉应力一般有以下情况,上部靠近井口位置的石油套管所受拉伸力很大,固井过程中和固井后螺纹接头都存在较大的预拉伸载荷[6]。当套管内出现高压流体流动时,会引起套管的鼓胀效应和温度效应,进而导致轴向拉力增大[12]。根据热采井和其他井筒的变温工况,定义了套管接头受拉应力的载荷及边界条件。考虑到接头在开发工程中可能面临的温度情况,进行了20、50、100、150、200、250及300 ℃下的温度-应力耦合分析。
图3为150 ℃时拉应力作用下模型的Von Mises应力分布。由图可知,在所定义的工况下,套管的最大Von Mises应力出现在接触面20号扣牙倒角处,应力值达到832.5 MPa,出现明显的塑性变形。1号扣牙上部倒角处也有一较大的应力区,应力值达到765.0 MPa。中间部分扣牙(2~19号)应力值都较小,分布规律基本一致,即随着扣牙号的增加,对应部位应力呈一个较小的上升趋势。在中间段扣牙接触面上,高接触压力段出现在扣牙承载面的倒角部位,其他部位为低压力段。在1、20和21号扣牙的整个承载面都出现了较大的接触压力分布,最大接触压力为606.2 MPa。随着温度载荷的升高,接触压力和Mises应力都有一个小范围的增大。
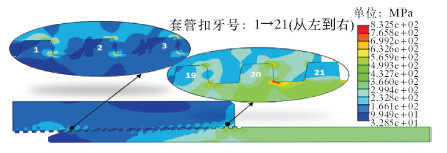
|
| 图 3 拉应力作用下模型的Von Mises应力分布 Fig.3 Von Mises stress distribution of the model under tensile stress |
温度对于轴向位移和径向位移的影响十分明显,随着温度的升高,轴向位移和径向位移值都呈上升趋势。300 ℃下接触对附近最大轴向位移达到0.859 mm,最大径向位移为1.003 mm。
产生以上情况的原因是:在螺纹接头承受拉压的工况下,轴向上可以充分地进行伸长变形,也就能充分地释放温度载荷所产生的热应力,从而导致不同温度载荷下,接头的Mises应力以及接触压力的增大都很小。
3.2 压应力作用下的耦合结果套管直接承受压缩载荷,极易产生径向变形,但是固井流程中会出现套管串底端活塞力向上作用,而且下部套管也有承受压应力的状况。除了热采井高温蒸汽的注入,高压酸化压裂作业也能导致温度载荷发生改变。如果井筒温度变化频繁,那么就有可能使管柱达到临界失稳载荷Ft。为了与受拉状态进行对比,压应力取值与拉应力相同。
图4为150 ℃时压应力作用下模型的Von Mises应力分布。
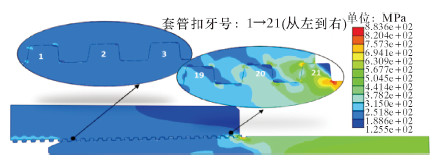
|
| 图 4 压应力作用下模型的Von Mises应力分布 Fig.4 Von Mises stress distribution of the model under compressive stress |
由图4可知,在所定义的工况下,Mises应力的最大值出现在21号扣牙齿根部,达到了883.6 MPa。接触压力的高压段出现在套管最后4扣的导向面部位,最大接触压力为966.2 MPa。温度载荷在径向位移上的作用规律与受拉工况一致,但在轴向上,热应力和压应力的作用方向相反,导致轴向位移分布不同,热应力在轴向位移上的影响比压应力和拉应力都明显,占主导地位。在温度载荷超过60 ℃以后,整个接触面的位移方向都发生改变。300 ℃时,接触面最大轴向位移为0.623 mm,比拉应力作用下小很多。Mises应力以及接触压力随着温度载荷的升高依然呈十分缓慢的增大趋势,原因是接头上的压应力不能充分约束热应力在轴向上的释放。
3.3 两端轴向位移受约束的耦合结果水泥面以上套管在固井质量良好时,其轴向位移通常受到约束,但是在这种工况下,井内的温度和压力一旦发生变化,就极易产生附加轴向力。
图5为不同温度载荷下管体的Von Mises应力分布。从图5a可以看出,随着温度载荷的升高,1、2号扣牙接触面的Mises应力逐渐增大,在温度载荷上升初期,Mises应力增大十分明显,但是150 ℃之后,Mises应力的增大速率明显减小。从图5b可以看出,20、21号扣牙接触面的Mises应力整体上也和温度载荷呈正相关,但是在某些部位,由于扣牙的轴向和径向变形速率不一致,导致Mises应力分布违反了这种规律。中间段扣牙Mises应力随温度变化的规律和首端扣牙基本一致。在两端轴向约束的工况下,升高温度载荷将导致塑性变形区域面积增大,塑性变形区主要分布在最后一扣的齿根部位。
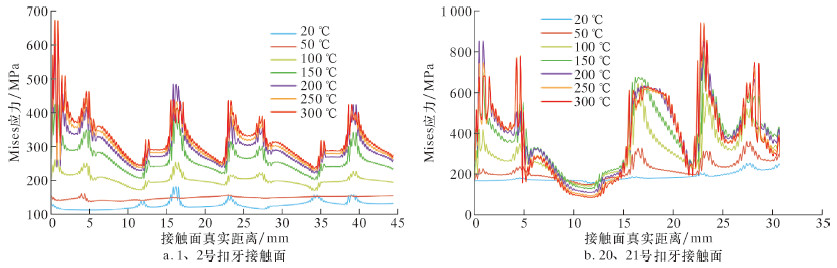
|
| 图 5 不同温度载荷下管体的Von Mises应力分布 Fig.5 Von Mises stress distribution of the casing body at different temperature loads |
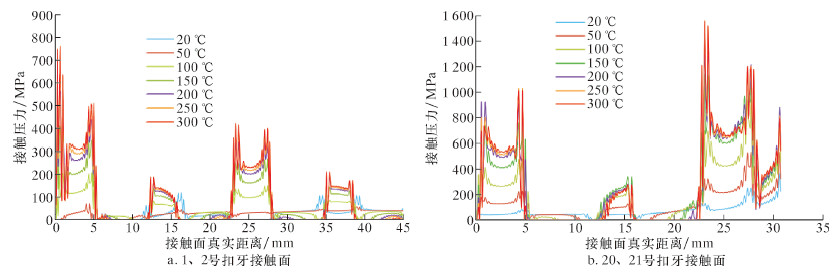
图6为不同温度载荷下管体的接触压力分布。从图可以看出,1、2、20和21号扣牙的整体接触压力都随着温度载荷的升高而增大。但是,由于轴向和径向变形速率不一致,致使某些部位接触压力分布发生改变,出现违反整体规律的现象。中间段扣牙接触压力也和温度呈正相关,在温度载荷较高时,接触压力随温度上升会增大的趋势变缓,因此200、250和300 ℃的接触压力曲线出现了近乎重叠的现象。300 ℃下,接头附近最大位移值为0.275 mm,相对于拉应力和压应力下的最大位移值1.328和1.105 mm小得多,说明热应力的释放受到了明显的约束,特别是轴向上的约束。3种工况下,套管内压和外压对径向上热应力释放的约束能力都比较有限。
|
| 图 6 不同温度载荷下管体的接触压力分布 Fig.6 The contact pressure distribution of the casing body at different temperature loads |
(1)偏梯形螺纹扣牙过盈接触时,比较不同扣牙的Mises应力和接触压力,呈现两端大、中间小的分布趋势,且在轴向受拉和受压工况下,温度载荷对Mises应力和接触压力的影响很小,接头附近位移变化十分明显。API标准偏梯形螺纹接头的接触面压力分布很不均匀,大部分扣牙接触面并没有有效地承担载荷。
(2)在螺纹接头两端轴向位移受约束的情况下,即通常水泥面以上套管所处工况下,温度载荷对于接触面的Mises应力和接触压力影响显著,两者均随着温度载荷的升高而增大,且在达到较高温度后趋势变缓。温度的升高虽然会增大接触压力,但是也会加剧扣牙接触面受力不均,使部分区域过早进入塑性变形。
(3)分析温度对套管接头力学行为的影响不能一概而论,必须考虑实际工况。热应力的有效释放是保证接头始终处于可靠状态的必要条件,在进行温度-应力耦合时必须保证边界条件的合理性,否则会对计算结果产生很大的影响。
| [1] | 练章华,韩建增,张毅,等.套管偏梯形和圆形螺纹滑脱载荷分析[J].石油机械,2004,32(5):7-9. |
| [2] | 高连新,金烨,史交齐.圆螺纹套管接头应力分布规律研究[J].机械强度,2004,26(1):42-48. |
| [3] | 陈守俊,李强,张毅,等.圆锥管连接螺纹牙变形及应力分布研究[J].中国机械工程,2010,21(17):2044-2049. |
| [4] | 韩传军,邱亚玲,刘清友,等.管柱螺纹连接计算中的圣维南效应分析[J].石油机械,2009,37(6):5-7,38. |
| [5] | 王建东,冯耀荣,林凯,等.特殊螺纹接头密封结构对比分析[J].中国石油大学学报:自然科学版,2010,34(5):126-130. |
| [6] | 许志倩,闫相祯,杨秀娟.特殊螺纹套管接头连接性能的安全可靠性分析[J].北京科技大学学报,2011,33(9):1146-1153. |
| [7] | 安文华,驼发前,吕拴录,等.塔里木油田特殊螺纹接头油套管评价试验及应用研究[J].钻采工艺,2010,33(5):84-88. |
| [8] | 祝效华,董亮亮,童华,等.拉弯复合载荷作用下的API短圆套管螺纹力学行为[J].石油学报,2013,34(1):157-163. |
| [9] | 祝效华,张智,常学军,等.复杂结构井磨损套管连接螺纹的三维力学行为[J].石油学报,2015,36(6):748-753. |
| [10] | 王树平,陈平,石晓兵,等.温度对套管接头螺纹接触压力的影响[J].西南石油学院学报,2005,27(4):63-65. |
| [11] | American Petroleum Institute.API specification 5B (specification for threading,gauging,and thread in-spection of casing,tubing,and line pipe threads)[S].4ed.Washington DC:API,2008. |
| [12] | 孙宝泉,徐治明,蔡庆俊,等.套管柱在高压工艺条件下的受力及保护浅析[J].石油机械,1995,23(3):36-40. |




