0 引 言
PDC钻头水力性能不良会导致钻头先期损坏、井眼清洁质量差及钻头泥包等问题[1, 2]。前人利用数值模拟和试验的方法对PDC钻头井底流场进行了大量研究[3, 4, 5, 6],但大多是针对圆形喷嘴钻头。在矩形喷嘴研究方面,管志川等[7]通过室内试验研究了矩形喷嘴的流量系数、轴心动压力衰减规律及横向动压力梯度的分布规律;黄奎林等[8]通过数值模拟研究了矩形喷嘴对PDC钻头井底速度场、压力场和流场结构的影响。研究中仍然存在以下不足:①将井底流场假设为钻井液的单相流场,不符合实际情况;②仅对速度场和压力场进行定性分析,没有给出判别井底流场优劣的参数。近年来,A.Moslemi等[9]提出了固液两相井底流场的研究思路,但其假设岩屑颗粒从井底面射入流场,并不符合实际情况。为此,笔者基于计算颗粒追踪法,将岩屑建模为从切削齿表面射入流场的固相颗粒,使用岩屑运移速度比作为钻头水力性能的评价参数,对矩形喷嘴PDC钻头的水力性能进行研究。
1 固液两相流动控制方程与岩屑运移速度比 1.1 液相流动控制方程通过估算流体雷诺数可知,井底流场为湍流流动。液相流动的基本定律是质量守恒定律、动量守恒定律和能量守恒定律,可得到连续方程、动量方程和能量方程,联立后得到三维不可压湍流流场的N-S方程,用标准的κ-ε湍流模型进行封闭[10]。
1.2 固相运动控制方程一般情况下,PDC钻头正常钻进产生的岩屑量对新产生的井眼体积占有率小于10%,因此满足离散相模型(DPM)的适用条件[11]。DPM通过积分拉格朗日坐标系下的颗粒作用力微分方程来求解离散相颗粒的轨迹。颗粒的作用力平衡方程(颗粒惯性等于作用在颗粒上的各种力)在笛卡尔坐标系下的形式(以x方向为例)为[12]:
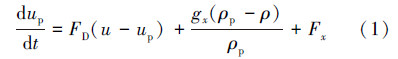
式中,up为颗粒速度,m/s;u为流体速度,m/s;ρp为颗粒密度,kg/m3;gx为重力加速度,m/s2;FD(u-up)为颗粒的单位质量曳力,N;Fx为其他单位质量作用力,N。
Fx主要包括视质量力(附加质量力)、压力梯度力、布朗力和Saffman举升力等。其中较重要的是附加质量力和压力梯度力,前者由颗粒周围流体加速而引起,后者由流场中存在的流体压力梯度引起。由于研究的颗粒尺寸处于毫米级别,计算中并未考虑布朗力和Saffman举升力。
式(1)对时间积分可以得到颗粒运动轨迹。轨道积分计算采用稳态追踪方式,每隔10个连续相流场迭代步,在当前流场状态下,逐个对每个颗粒进行从初始位置到终了位置的轨道积分计算及源项计算,得到某一时刻连续相流场状态下一系列积分时间步的颗粒状态,一系列颗粒位置可连成运动轨迹线,从而实现计算颗粒追踪。
1.3 岩屑运移速度比为反映PDC钻头水力性能的优劣,使用岩屑运移速度比Ct作为评价指标,其定义为通过某一截面的岩屑平均运移速度与钻井液平均流速之比,计算公式为:

式中,vpa为岩屑平均运移速度,m/s;vfa为钻井液平均流速,m/s。
显然,Ct值越大,说明井底岩屑运移效率越高,钻头水力性能越强。
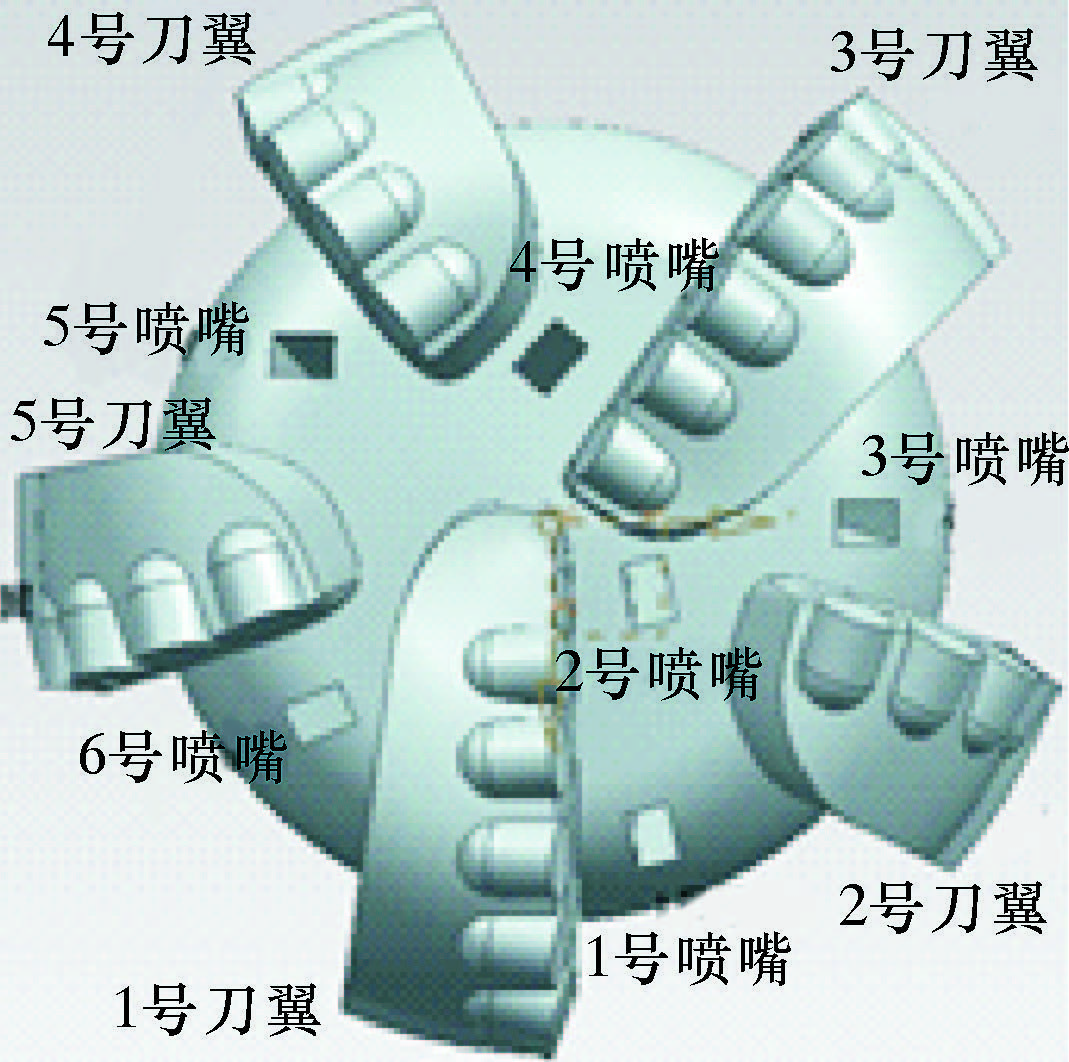
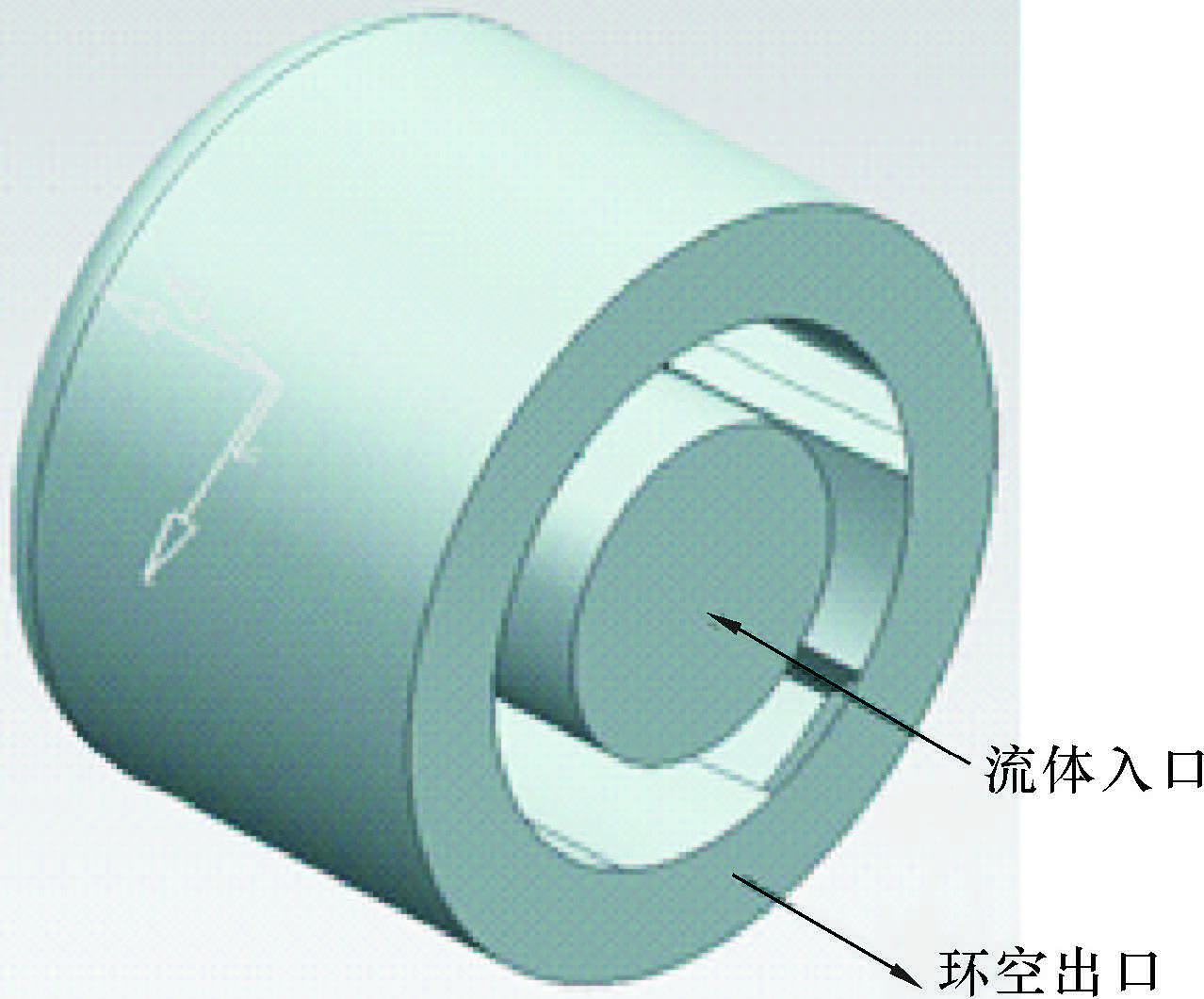
2 模型建立选择油田常用的直径为215.9 mm、5刀翼、布置6个矩形喷嘴的PDC钻头作为基础研究模型,喷嘴当量直径为12 mm,长宽比为1.5,模型如图1所示。以钻头模型为基础,建立如图2所示的流域模型,其中井筒直径D=227.0 mm(假设扩径5%)。
|
| 图 1 布置6个矩形喷嘴的PDC钻头 Fig.1 The PDC bit with six rectangular nozzles |
|
| 图 2 流域模型 Fig.2 Flow volume model |
网格划分采用非结构化网格,为确保计算结果的准确性,在流速变化较大的位置(例如井底和喷嘴进出口)进行局部细化,并进行了计算结果网格无关性验证,最后确定网格数约为200万。
入口边界条件采用速度入口。速度大小根据工作排量进行估算,设置排量为30 L/s,换算得入口速度为3.8 m/s。 出口边界条件采用压力出口。出口静压力值根据井深估算,设定井深为3 000 m,钻井液密度为1 200 kg/m3,计算得出口压力为35 MPa。
采用固体壁面边界条件。假设整个流场的固体边界上无热量传递,满足壁面无滑移条件,近壁区采用壁面函数法处理。DPM边界条件为reflect。
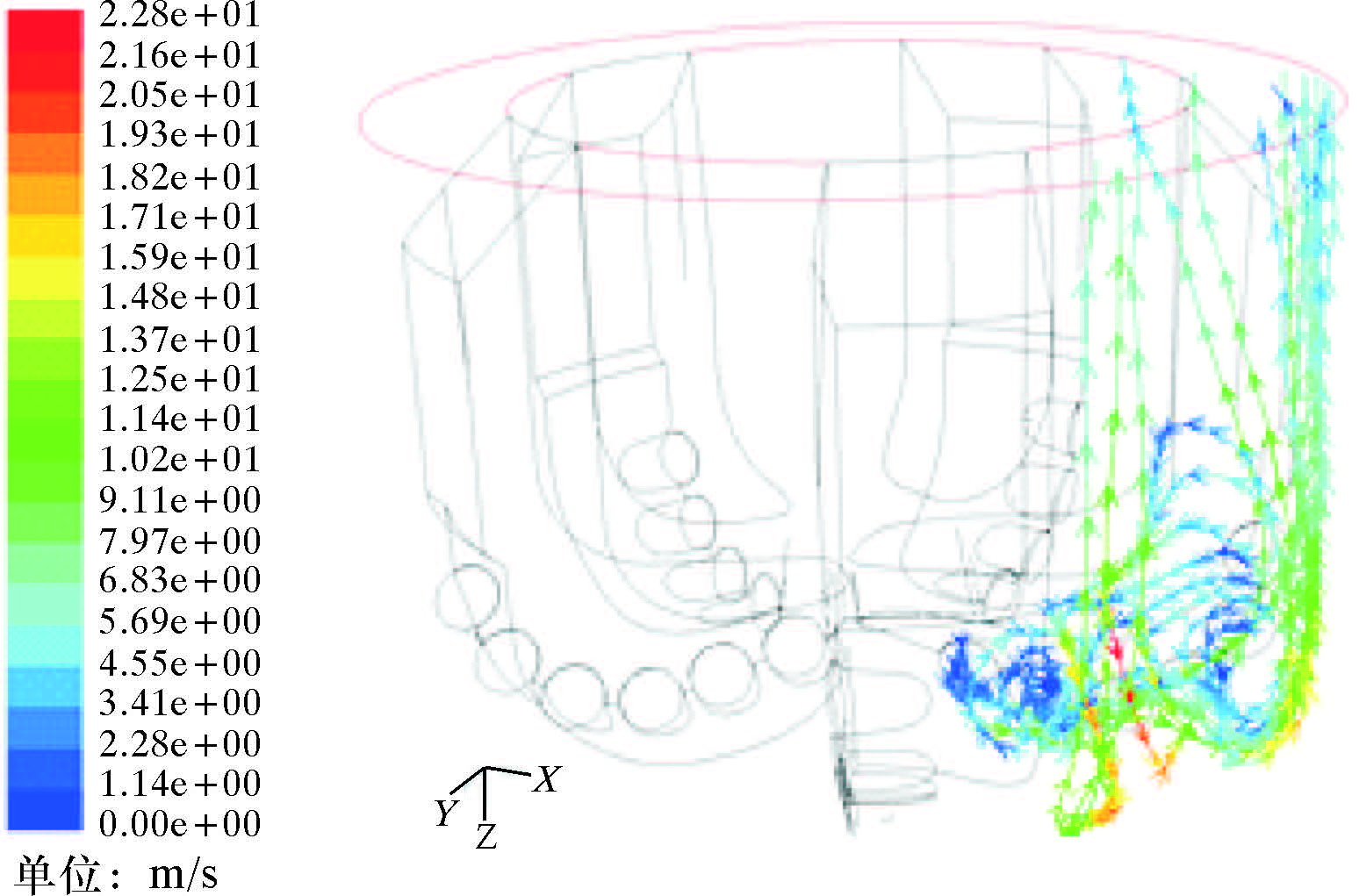
3 数值计算结果与分析以1号刀翼为例,岩屑颗粒运移轨迹如图3所示。由图可知,岩屑颗粒从切削齿表面产生,受井底流场的影响,沿着三维不规则的轨迹向环空出口运动;在井底附近时,由于存在流速较大的漫流层,岩屑颗粒运动速度较大,最大可达22.8 m/s,随着运移过程的继续,由于受到运动阻力的影响,同时撞击钻头体和井壁会发生反弹,动能损耗较大,速度逐渐下降,到达环空出口时,运动速度为3.0 m/s左右。
|
| 图 3 岩屑颗粒运移轨迹(颜色代表运动速度) Fig.3 Cutting particles migration track (colored by particle velocity magnitude) |
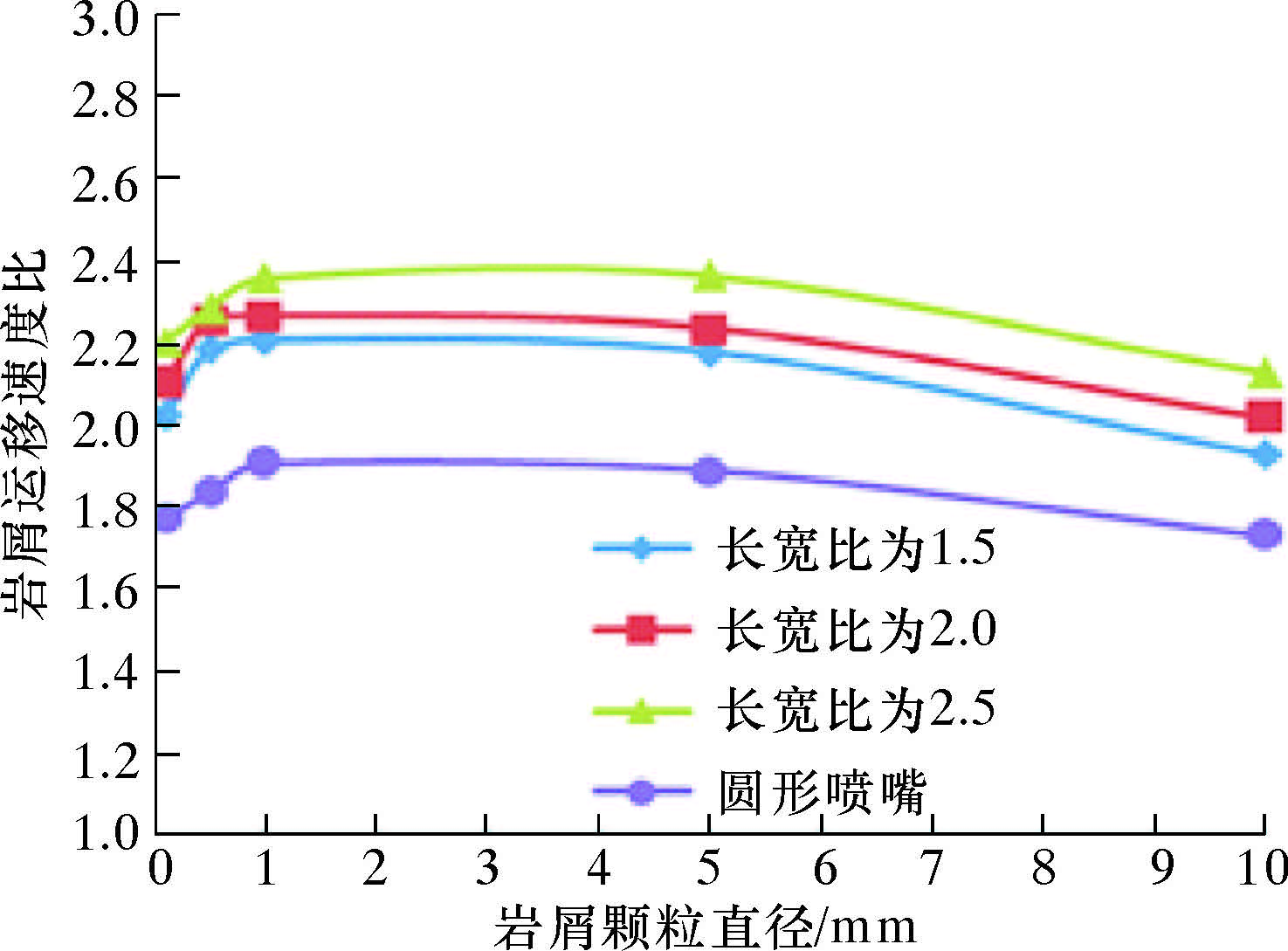
为量化研究矩形钻头水力性能,使用岩屑运移速度比Ct作为评价参数。不同岩屑直径(0.1、0.5、1.0、5.0、10.0 mm)条件下,不同长宽比(1.5、2.0、2.5)的矩形喷嘴钻头环空出口截面上的Ct值与相同当量直径的圆形喷嘴钻头Ct值的对比如图4所示。由图可知,在相同岩屑尺寸条件下,矩形喷嘴钻头的Ct值大于圆形喷嘴钻头的Ct值,且随着长宽比的增大而增大;对于同一钻头,直径1.0 mm岩屑的Ct值最大,当岩屑直径小于1.0 mm时,Ct随岩屑直径的增大而增大,当岩屑直径大于1.0 mm时,Ct随岩屑直径的增大而减小,此规律与A.Moslemi[9]的数值模拟结果一致。分析原因为:岩屑直径增大时,动能增大,同时运动阻力(主要是重力)也增大,两者之间的权衡关系决定了的Ct大小,岩屑直径为1.0 mm时达到最优。
|
| 图 4 矩形喷嘴钻头Ct值与圆形喷嘴Ct值的对比 Fig.4 Comparison of Ct of bit with rectangular nozzles and circular nozzles |
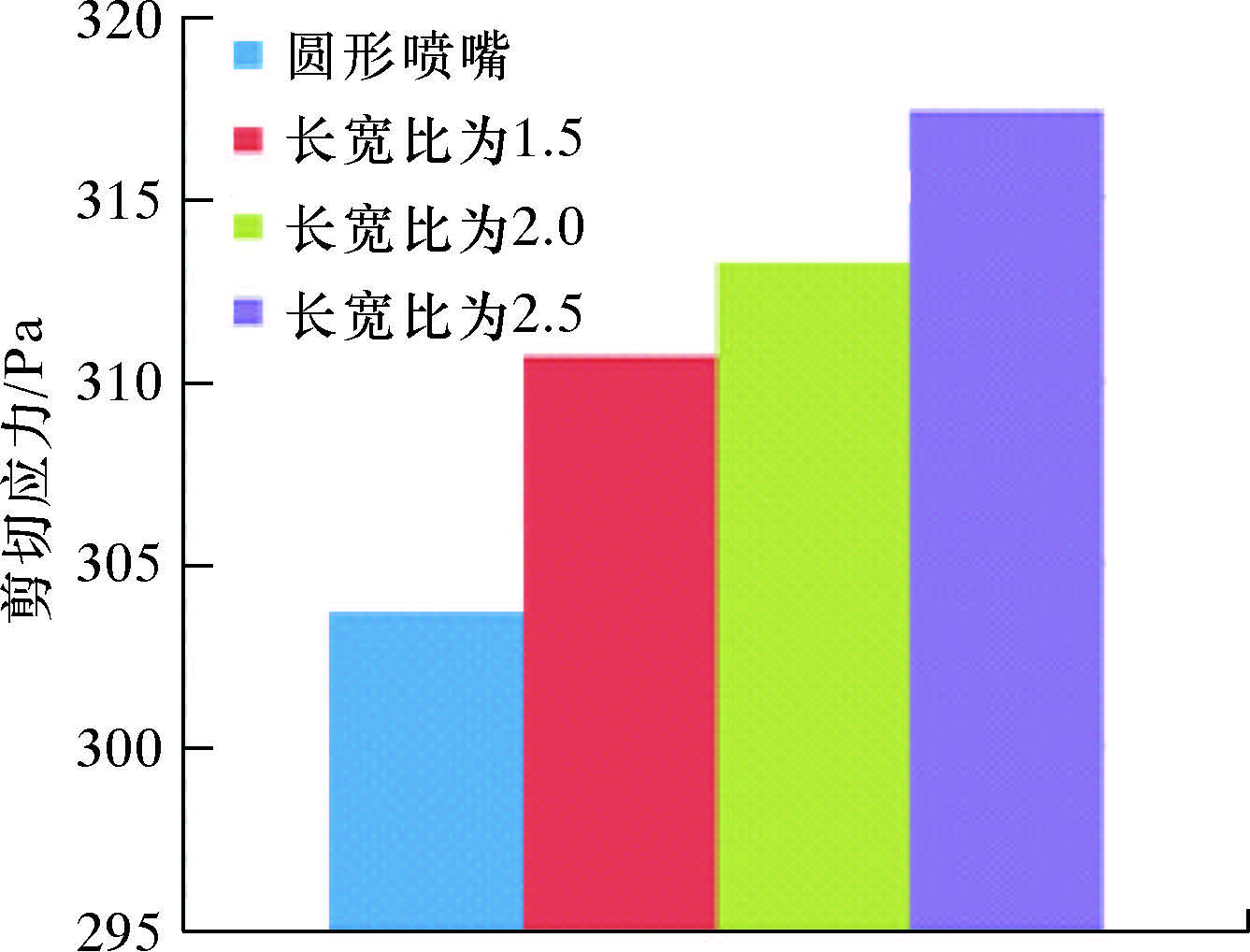
为分析矩形喷嘴长宽比对Ct影响规律的原因,以3号刀翼为例,分析不同长宽比矩形喷嘴和圆形喷嘴情况下的剪切应力大小,如图5所示。由图可知,与圆形喷嘴钻头相比,矩形喷嘴钻头的3号刀翼表面剪切应力值更高,而且长宽比越大,其值越大,与Ct值的变化规律一致。
|
| 图 5 3号刀翼表面剪切应力值 Fig.5 Surface shear stress of blade 3 |
由此可见,与圆形喷嘴相比,矩形喷嘴能够提高刀翼表面附近的钻井液流速,且提高程度与长宽比呈正相关关系。
另外,文献[8]中的研究发现,矩形喷嘴钻头的表面流速大于圆形喷嘴钻头的表面流速,圆形喷嘴在切削齿表面及齿基附近的低速区域大于矩形喷嘴钻头;圆形喷嘴钻头刀翼周围的涡漩多于矩形喷嘴钻头。综上所述,矩形喷嘴钻头的水力性能优于圆形喷嘴钻头。
4 结 论(1)基于计算颗粒追踪法,使用岩屑运移速度比Ct作为评价参数,建立了一种量化研究矩形喷嘴PDC钻头水力性能的方法。
(2)井底岩屑运移是三维不规则运动,沿程存在碰撞与反弹。在岩屑从井底向环空出口运动的过程中,速度逐渐减小。
(3)相同条件下,矩形喷嘴钻头的Ct值大于圆形喷嘴钻头的Ct值,且随长宽比的增大而增大。与圆形喷嘴钻头相比,矩形喷嘴钻头的水力性能更好,且长宽比越大越好。
(4)对于同一钻头,直径1.0 mm岩屑的Ct值最大,当岩屑直径小于1.0 mm时,Ct随岩屑直径的增大而增大,当岩屑直径大于1.0 mm时,Ct随岩屑直径的增大而减小。
| [1] | 陈修平,邹德永.PDC钻头泥页岩地层钻进泥包机理及对策研究进展[J].天然气工业,2014,34(2):87-91. |
| [2] | Hanna C,Douglas C H S,Asr H,et al.Application specific steel body PDC bit technology reduces drilling costs in unconventional North America Shale Plays[C]//SPE Annual Technical Conference and Exhibition.Society of Petroleum Engineers,2011. |
| [3] | 黄红梅,翟应虎,王辉,等.实体PDC钻头流场数值模拟与实验验证[J].石油大学学报:自然科学版,2005,29(3):49-52. |
| [4] | 郑胜,王宏光,杨爱玲,等.PDC钻头切削表面流场挟沙能力分析[J].上海理工大学学报,2002,24(4):345-348. |
| [5] | Watson G R,Barton N A.Using new computational fluid dynamics techniques to improve PDC bit performance[R].SPE 37580-MS,1997. |
| [6] | 侯成,李根生,黄中伟,等.定向喷嘴PDC钻头井底流场特性研究[J].石油钻采工艺,2010,32(2):15-18. |
| [7] | 管志川,陈庭根,蔡镜仑.用矩形出口喷嘴改善PDC钻头水力结构的研究[J].石油大学学报:自然科学版,1992,16(2):20-28. |
| [8] | 黄奎林,杨迎新,钱雯,等.矩形喷嘴对PDC钻头井底流场影响的研究[J].机械研究与应用,2012(2):27-29. |
| [9] | Moslemi A,Ahmadi G.Study of the hydraulic performance of drill bits using a computational particle-tracking method[R].SPE 169812,2014. |
| [10] | 陶文铨.数值传热学[M].西安:西安交通大学出版社,2003:123-126. |
| [11] | 龙天渝,苏亚欣,向文英.计算流体力学[M].重庆:重庆大学出版社,2007:29-33. |
| [12] | Baxter L L,Smith P J.Turbulent dispersion of particles[J].The STP Model Energy & Fuels,1993(7):852-859. |



