0 引 言
随着海上油田加密调整技术的广泛应用,原有的密集丛式井井网密度进一步增大,导致加密调整井出现碰撞的风险越来越高,且在实际钻井过程中多次出现碰撞老井网的险情。井眼碰撞事故的发生会严重影响油田正常生产,造成巨大经济损失,如何在丛式井和加密调整井的钻井过程中预防井眼的碰撞已经变得十分迫切。
2010年,壳牌石油公司的L.Forster等[1]提出了基于分布式光纤检测技术的防碰监测方法。2011年,斯伦贝谢公司的R.Lowdon等[2]研发了基于振动分析的邻井防碰系统。为了满足监测需求,井队工作人员需要不停地开关泵和改变钻头转速,耗费较多的人力和时间,影响钻井时效。2011年,Clampon公司的G.Instanes等[3]也发明了一套基于监测邻井钻头振动信号的防碰系统,不过其采用的是非侵入式超声传感器,其监测效果无法获知。2013年,中海油田服务股份有限公司的曹阳等[4]研究发明了一种新的在钻井作业中防碰绕障的方法和系统,但是该方法需要重复多点测量井眼轨迹参数。为保障钻井作业安全顺利地进行,迫切需要研究一种新的井眼防碰技术。笔者所在课题组针对现场防碰需求,受“人工监听”的启发,研究了基于振动信号监测的丛式井地面防碰监测系统[5],并进行了现场应用,取得了较好的防碰效果。为了能够精确计算在钻井与风险井之间的距离,笔者建立了基于钻头振动信号的丛式井井间距离计算模型,并对模型的效果进行了试验验证。
1 丛式井井间距离计算模型钻头振动波在地层中传播时,由于地层介质的吸收衰减和波的扩散衰减作用,振动波的能量逐渐耗散;而振动波在套管中传播时,由于套管的色散效应和胶结介质的吸收作用,同样也造成振动波能量在一定程度上耗散。因此,在地面套管头处采集到的振动信号的能量是关于钻头振动波强度、钻头与邻井套管井间距离、地层介质和套管的衰减系数、井深和钻井工况的函数[6]。根据振动波的衰减规律,建立适当的函数关系,可求得钻头距风险邻井套管间的距离。
1.1 井间距离的计算钻头产生的振动波在地层及套管中传播时,其衰减规律会受到很多因素的影响,为使问题得到简化,首先做出如下假设,然后在这些假设的基础上建立适用于浅层井段的井间距离计算模型。
(1)钻头产生的振动波为球面波。钻头破碎岩石产生振动波,此时钻头相当于地层中的点源,其振动波的波阵面为球面,波在地层中传播时既会发生扩散衰减,又会发生吸收衰减。
(2)一开阶段井型为垂直井。由于一开阶段对井身质量有严格要求并且井深较小,可近似认为一开阶段各邻井及正钻井井型为垂直井,方便钻塞过程中对衰减系数的确定。
(3)浅层井段地层岩性和物性基本一致。
(4)由于浅层为松软的砂泥岩,主要考虑地层对钻头产生的振动波的吸收衰减效应。
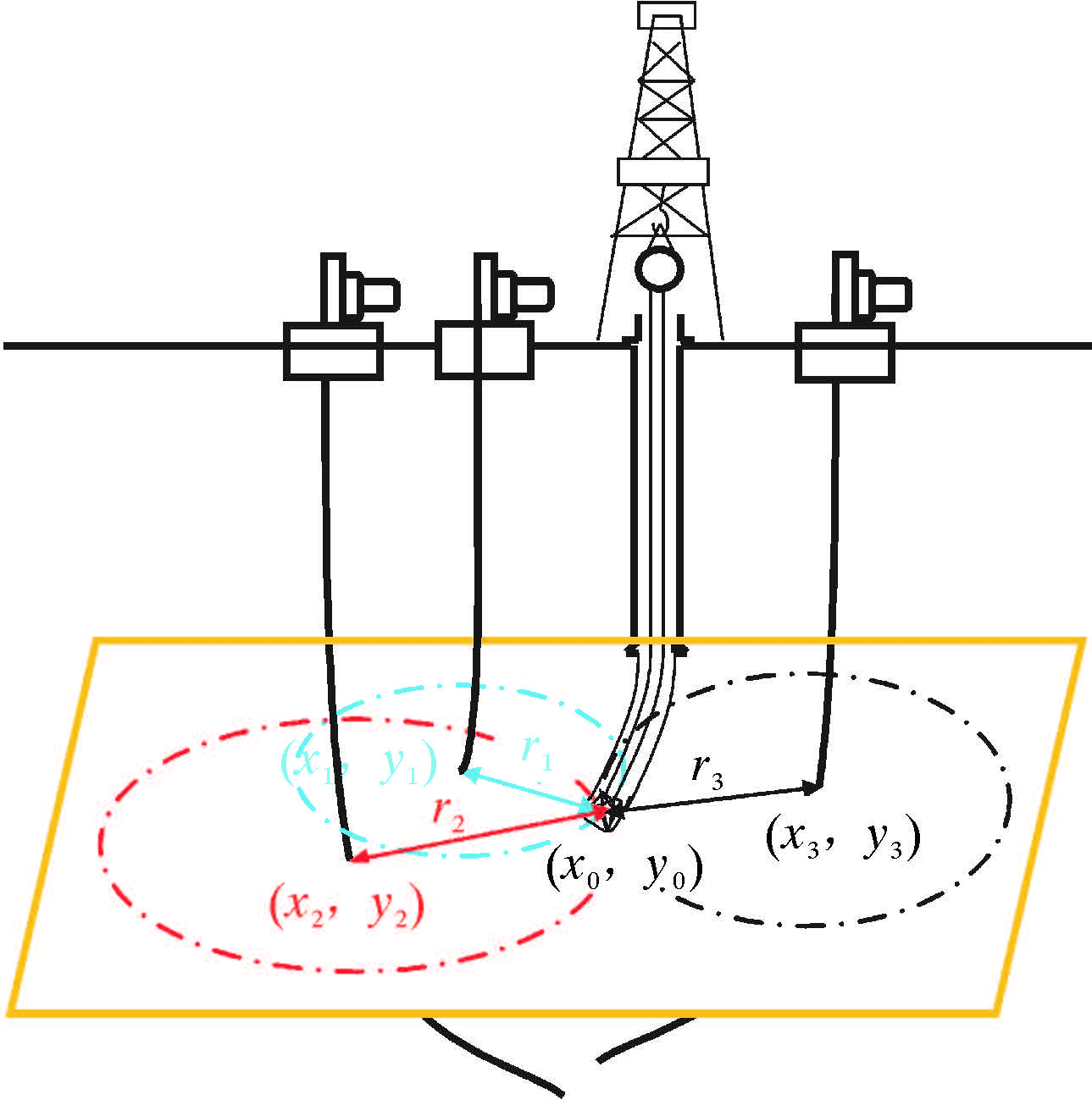
根据假设条件和振动波的衰减规律,以存在3口以上风险邻井的监测井为例,建立井间距离计算模型,如图1所示。正钻井钻头距风险邻井套管的距离为ri(i=1,2,3),根据振动波在井间地层中的传播理论可知,当振动波传播至邻井套管时,振动波的幅值和井间距的关系为[7]:
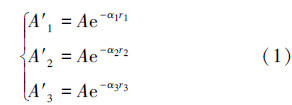
|
| 图 1 井间距离计算模型示意图 Fig.1 Schematic of inter-well distance calculation model |
式中,A为钻头(震源)处的振动波幅值强度,mm/s2;A′i为风险邻井井底接收到的振动波幅值,mm/s2,i=1,2,3;α为振动波在地层中传播的衰减系数,m-1。
由振动波在风险邻井套管中的传播规律可知,振动波由套管防碰点传播到套管头,并被加速度传感器接收到时,信号幅值与井深的关系如下。
对于正钻井:

对于风险邻井:
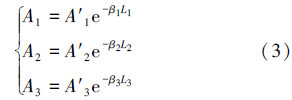
式中,Ai为风险邻井套管头处采集的振动波幅值,mm/s2,i=1,2,3;Li为套管防碰点至井口套管头的套管长度,m,i=1,2,3;βi为振动波在套管中传播的衰减系数,m-1,i=1,2,3。
每口风险邻井在整个监测过程中振动波幅值为:
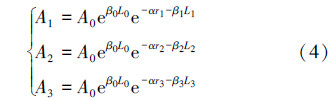
于是风险邻井在井深Li0、Li1处采集到的振动波幅值为:
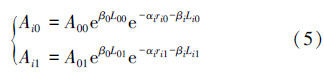
两者相比得到:
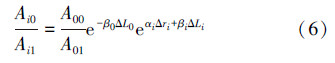
即有:
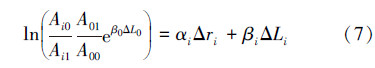
对于式(7)而言,在钻井和风险井套管头处的振动波幅值均为已知量;ΔL0、ΔLi分别为在钻井与风险井井深差,为已知量;地层衰减系数以及套管衰减系数均可通过实测数据结合防碰扫描数据反推得出。故依据以上数据,可计算得到风险邻井不同井深处的井间距差值为:
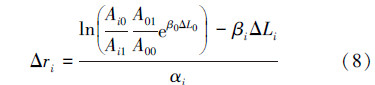
在考虑地层和套管衰减系数不同的情况下,该距离计算模型建立了不同井深下相对振幅与井间距差值的关系,避免了振动信号强度变化、井下复杂磁场造成的测量方位角误差以及套管型号下入方式不同对计算结果的影响。
1.2 衰减系数的确定由于钻塞过程钻井参数基本相同并且塞面以上井段可看作垂直井,所以选取此过程来计算衰减系数。为简化计算,假设探塞过程正钻井和风险邻井井深为垂深,即正钻井和风险邻井套管衰减长度相同。
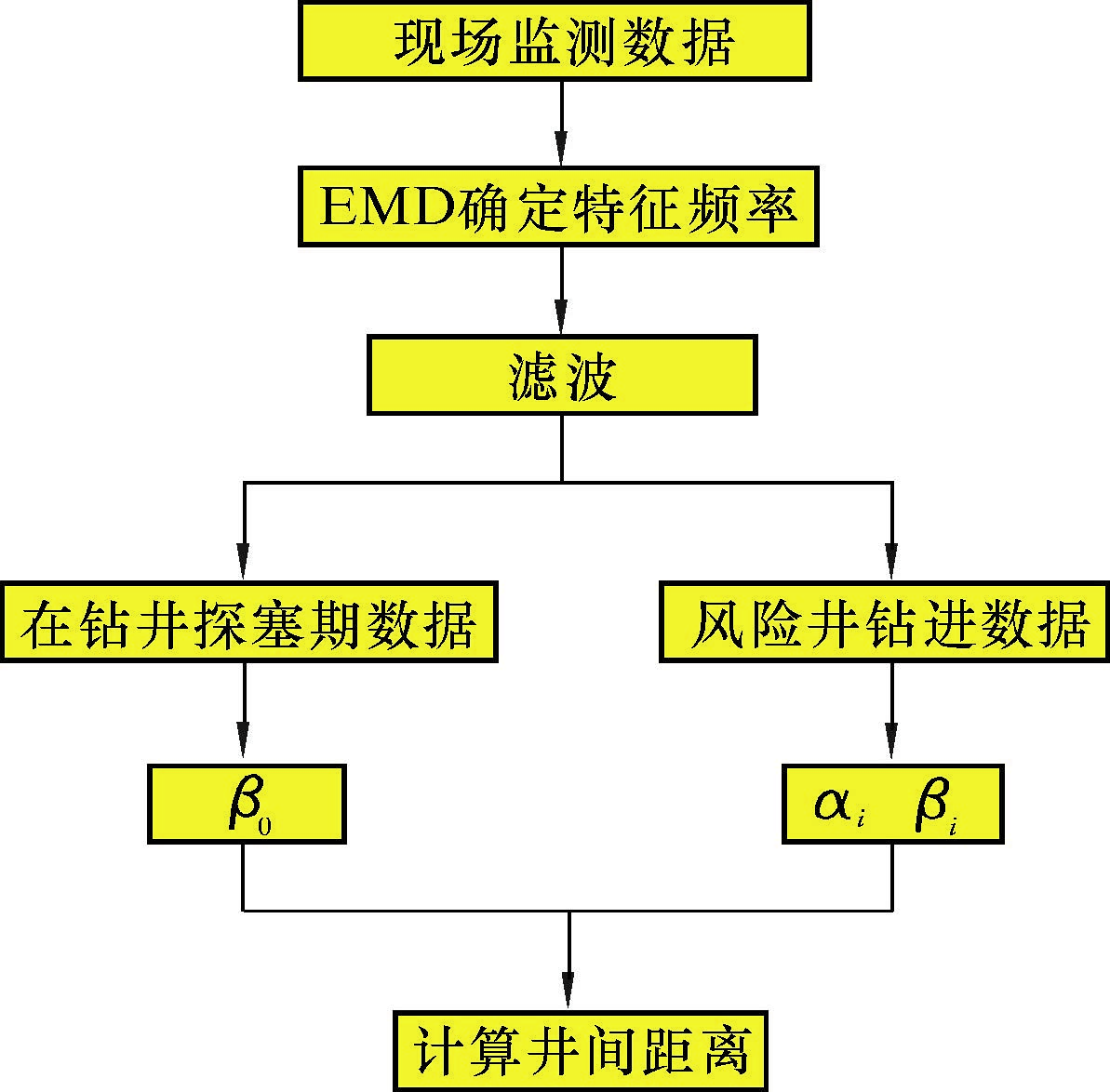
利用式(2),对不同井深下正钻井套管头处传感器接收到的振动幅值进行拟合,可得正钻井套管衰减系数β0。但由于探塞期各风险邻井的井间距基本不变,无法利用井距差进行有效的数据拟合,所以选取出塞的一段监测数据,结合公式(7)对Δri和ΔLi进行回归分析,得到地层衰减系数αi和套管衰减系数βi。得到各个参数后,利用式(8)计算得到风险邻井不同井深处的井间距差值Δri,与上一测点的井间距相加即为风险邻井在该井深下的井间距离。模型计算流程如图2所示。
|
| 图 2 井间距离计算模型流程图 Fig.2 The flow chart of inter-well distance calculation model |
本次现场试验在西江某平台进行,截至2014年5月,该平台累计完成92口井作业,目前在生产井30口,累计产油3 461万m3,综合含水体积分数97.1%,采出程度55.0%。为延缓油田产量递减速度,达到稳油控水目的,结合西江油田群的作业实际,计划使用低效井B26井(26#井槽)侧钻B26ST1井。结合防碰扫描数据得正钻井B26ST1的重点风险邻井为B25,分支井B23。
2.2 钻头振动信号的提取钻头振动信号是一种非平稳和非线性的宽频信号,现场所采集的信号不仅仅是钻头的振动信号,还包含各种机械设备工作和钻柱在井眼中的运动信号等。包含钻头振动特征的信号被各种各样的“噪声”淹没,因而从其中提取钻头的特征信号尤为重要。信号的时域和频域等普通分析方法已无法满足需求,必须采用先进的适用于非平稳信号研究的先进方法。 经验模态信号分解主要依据其自身特点,将固有模态函数从信号中抽取出来,无须提前设定任何基函数,适用于分析非平稳和非线性信号,信噪比相对较高,具有明显的优势[8, 9, 10]。
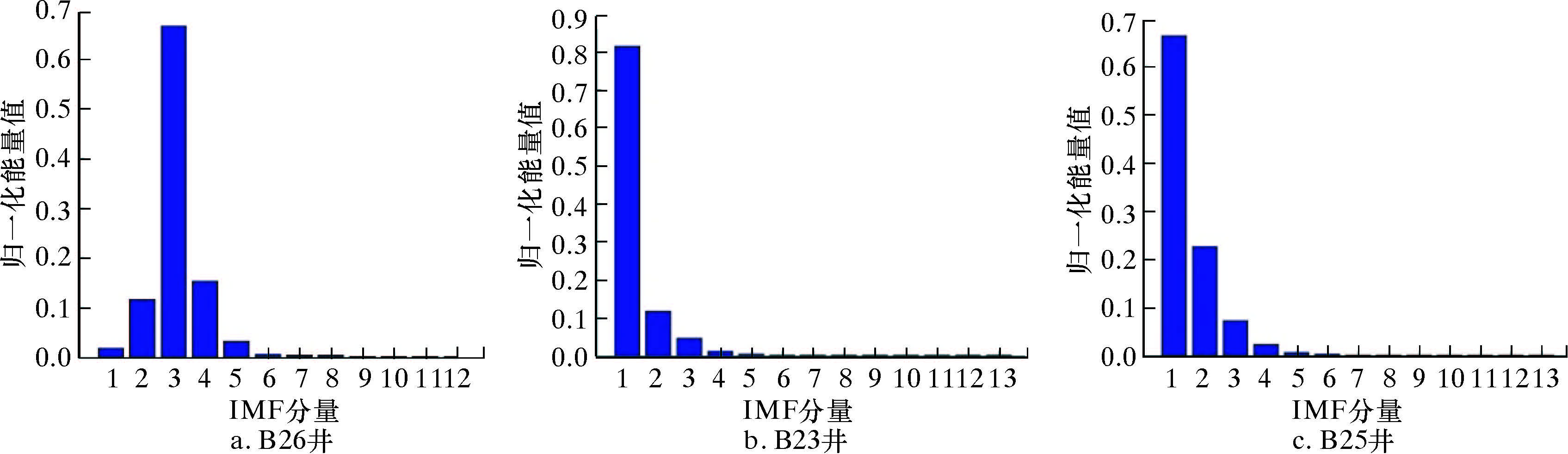
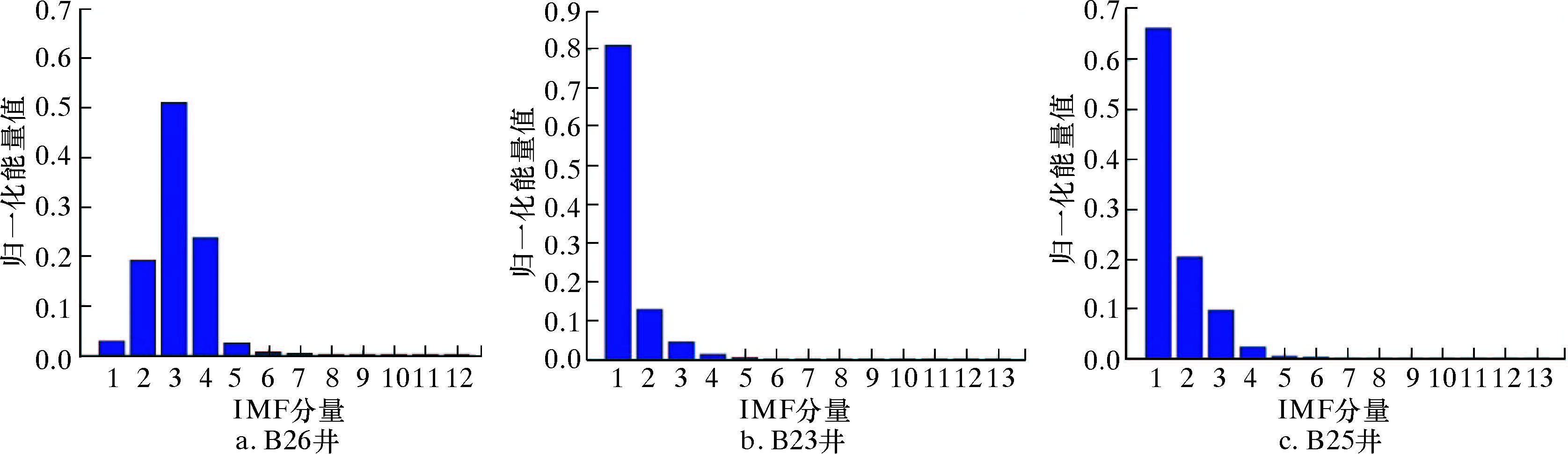
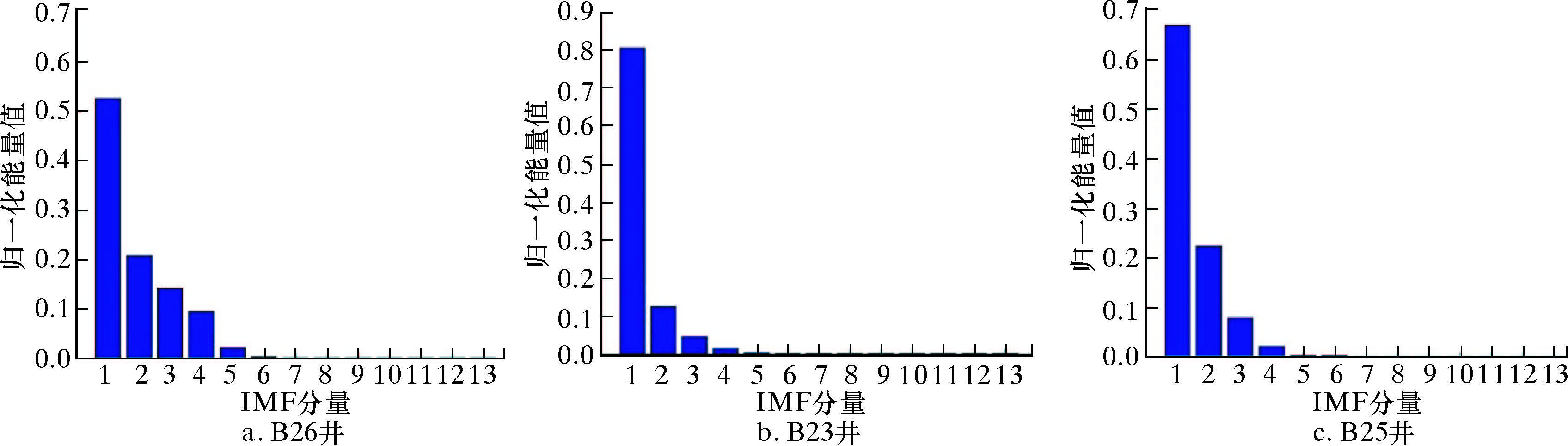
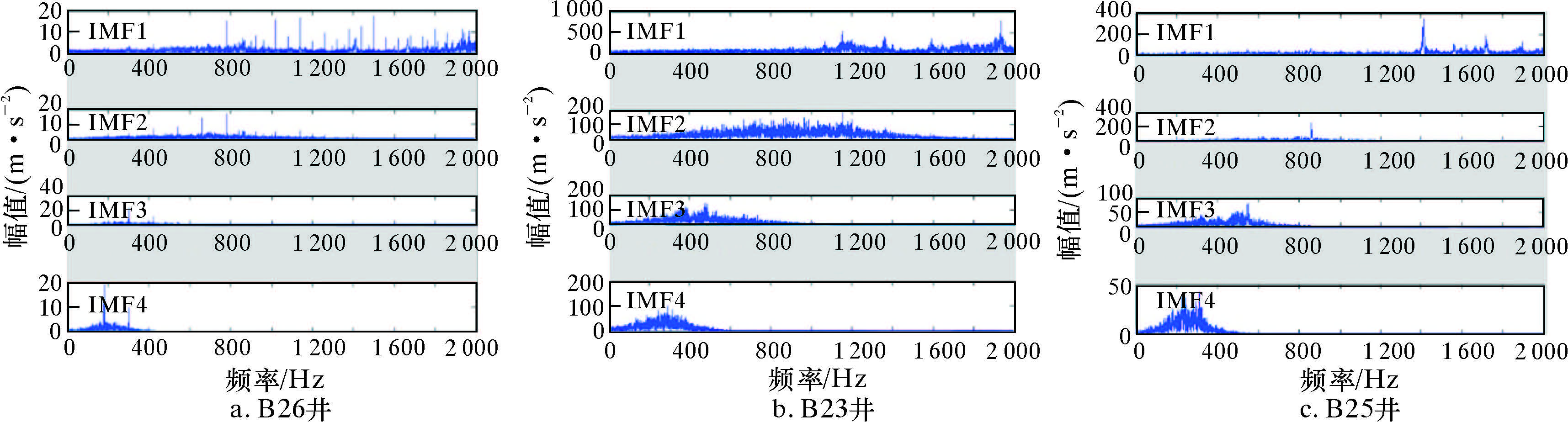
对采集到的振动信号进行EMD分解,如图3、图4和图5所示,信号能量主要集中在前4个IMF分量,因此对振动信号的IMF1~IMF4分量进行时频分析。结果显示,各井中IMF4分量的波动情况基本一致,包含钻头的振动信号。由图6的振动信号频域谱可知,IMF4分量主要集中在200~400 Hz,因此该频段可以作为钻头振动信号的特征频率。
|
| 图 3 501 m振动信号的归一化能量图 Fig.3 Normalized energy diagram of vibration signal at 501 m |
|
| 图 4 504 m振动信号的归一化能量图 Fig.4 Normalized energy diagram of vibration signal at 504 m |
|
| 图 5 590 m振动信号的归一化能量图 Fig.5 Normalized energy diagram of vibration signal at 590 m |
|
| 图 6 590 m振动信号的频域谱 Fig.6 Frequency domain of vibration signal at 590 m |
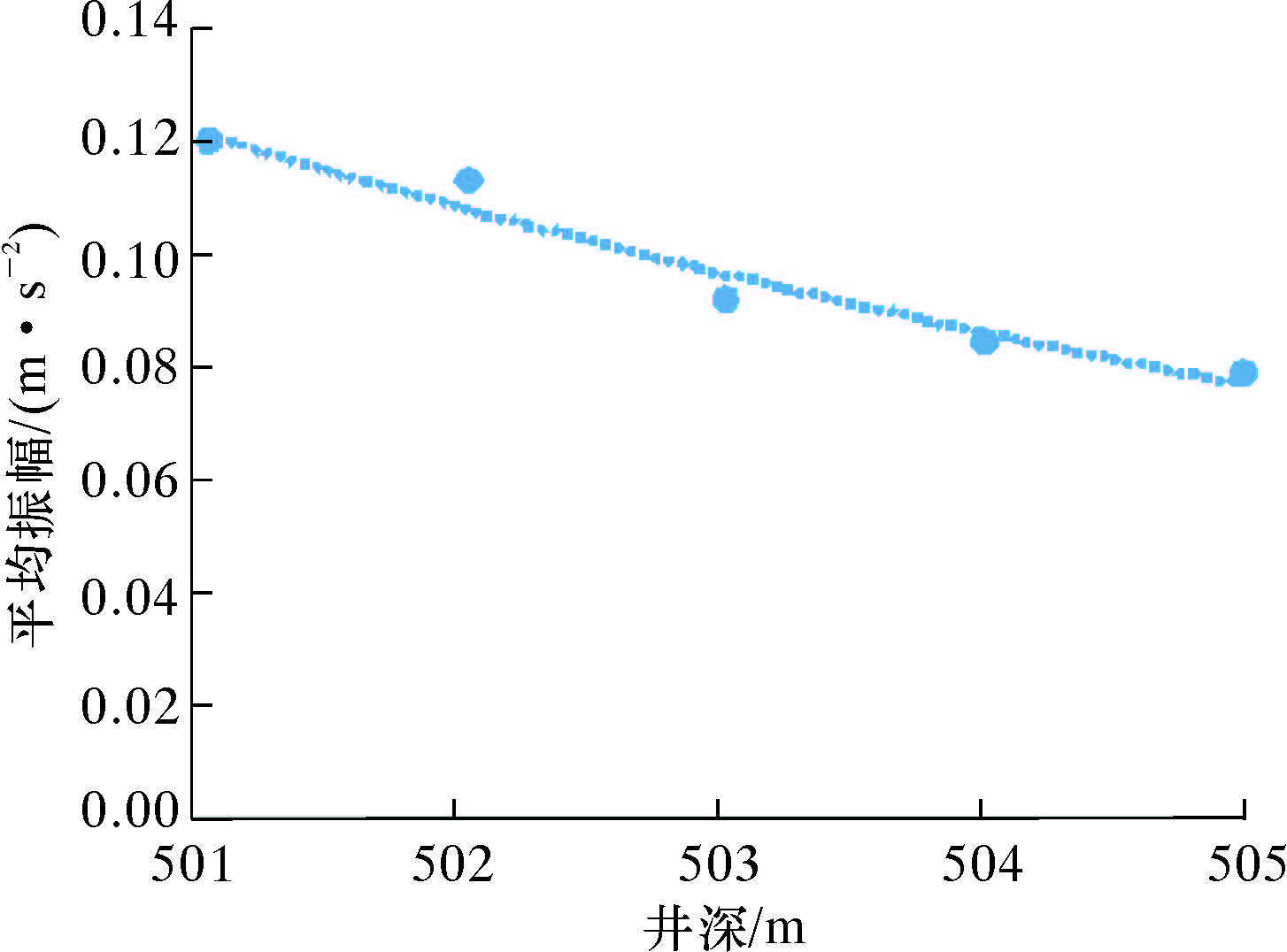
对现场监测数据进行200~400 Hz滤波,并计算滤波后振动信号的平均幅值,由探塞期(501~505 m)数据绘制在钻井B26的信号衰减曲线,如图7所示,求得衰减系数β0=0.113 0。
|
| 图 7 探塞期B26井振动信号衰减曲线 Fig.7 The attenuation curve of vibration signal in Well B26 during plug detection |
依据505~556 m监测数据,求取风险邻井振幅比值的对数值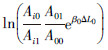 ,结果如表1和表2所示。
根据表1和表2数据,对振幅比对数值关于井距差和井深差进行回归分析,可得到B25和B23井的衰减系数。
,结果如表1和表2所示。
根据表1和表2数据,对振幅比对数值关于井距差和井深差进行回归分析,可得到B25和B23井的衰减系数。
| 井深差/ m | 井深/ m | B25井平均振幅/ (m·s-2) | B25井振 幅比值 | B26井平均振幅/ (m·s-2) | B26井振 幅比值 | 振幅比 对数值 | 井距差/ m | B25井扫描 井距/m |
| — | 505 | 0.044 8 | — | 0.080 7 | — | — | — | 28.00 |
| 5 | 510 | 0.046 5 | 0.963 4 | 0.087 4 | 1.083 0 | 0.607 5 | 0.87 | 28.87 |
| 5 | 515 | 0.049 2 | 0.945 1 | 0.008 5 | 0.097 3 | -1.821 9 | 0.85 | 29.72 |
| 5 | 520 | 0.042 6 | 1.154 9 | 0.010 1 | 1.188 2 | 0.881 5 | 0.82 | 30.54 |
| 3 | 523 | 0.038 1 | 1.118 1 | 0.009 7 | 0.960 4 | 0.410 2 | 0.47 | 31.01 |
| 2 | 525 | 0.050 1 | 0.760 5 | 0.009 8 | 1.010 3 | -0.037 6 | 0.32 | 31.33 |
| 15 | 540 | 0.050 0 | 1.002 0 | 0.007 9 | 0.806 1 | 1.481 5 | 2.40 | 33.73 |
| 5 | 545 | 0.043 8 | 1.141 6 | 0.009 8 | 1.240 5 | 0.912 9 | 0.80 | 34.53 |
| 4 | 549 | 0.042 5 | 1.030 6 | 0.009 6 | 0.979 6 | 0.461 5 | 0.64 | 35.17 |
| 7 | 556 | 0.038 3 | 1.109 7 | 0.015 2 | 1.583 3 | 1.354 6 | 1.09 | 36.26 |
| 井深差/ m | 井深/ m | B23井平均振幅/ (m·s-2) | B23井振 幅比值 | B26井平均振幅/ (m·s-2) | B26井振 幅比值 | 振幅比 对数值 | 井距差/ m | B23井扫描 井距/m |
| — | 505 | 0.120 9 | — | 0.080 7 | — | — | — | 9.37 |
| 5 | 510 | 0.138 1 | 0.875 5 | 0.087 4 | 1.083 0 | 0.511 7 | -0.12 | 9.25 |
| 5 | 515 | 0.123 9 | 1.114 6 | 0.008 5 | 0.097 3 | -1.656 9 | -0.13 | 9.12 |
| 5 | 520 | 0.113 9 | 1.087 8 | 0.010 1 | 1.188 2 | 0.821 6 | -0.11 | 9.01 |
| 3 | 523 | 0.119 1 | 0.956 3 | 0.009 7 | 0.960 4 | 0.253 9 | -0.06 | 8.95 |
| 2 | 525 | 0.110 9 | 1.073 9 | 0.009 8 | 1.010 3 | 0.307 6 | -0.03 | 8.92 |
| 15 | 540 | 0.134 5 | 0.824 5 | 0.007 9 | 0.806 1 | 1.286 5 | 0.09 | 9.01 |
| 5 | 545 | 0.134 1 | 1.003 0 | 0.009 8 | 1.240 5 | 0.783 5 | 0.18 | 9.19 |
| 4 | 549 | 0.136 1 | 0.985 3 | 0.009 6 | 0.979 6 | 0.416 6 | 0.22 | 9.41 |
| 7 | 556 | 0.125 1 | 1.087 9 | 0.015 2 | 1.583 3 | 1.334 8 | 0.52 | 9.93 |
以B23井610和620 m 2个测点为例计算井间距。已知β0=0.113 0、α2=1.941 6、β2=0.061 5,610 m测点井间距为9.15 m,由式(8)得:
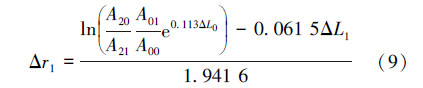
将B25和B26井2测点的监测数据代入公式(9),计算得Δr2=0.216 3 m,则630 m测点的井间距为:9.150 0 m+0.216 3 m=9.370 0 m。以此类推,求得的井间距数据如表3和表4所示。
| 井深/ m | 计算井距 差/m | 实际井 距/m | 计算井 距/m | 井距误 差/% |
| 570 | 2.28 | 38.27 | 38.54 | 0.71 |
| 580 | 1.59 | 39.58 | 40.13 | 1.37 |
| 590 | 1.63 | 40.77 | 41.21 | 1.06 |
| 610 | 3.04 | 42.90 | 44.24 | 3.04 |
| 620 | 1.60 | 43.85 | 44.50 | 1.46 |
| 630 | 1.70 | 44.73 | 46.20 | 3.19 |
| 660 | 4.83 | 47.12 | 49.56 | 4.91 |
| 670 | 1.45 | 47.88 | 51.01 | 6.13 |
| 680 | 1.70 | 48.64 | 49.58 | 1.90 |
| 690 | 1.61 | 49.44 | 51.19 | 3.41 |
| 700 | 1.50 | 50.27 | 50.94 | 1.31 |
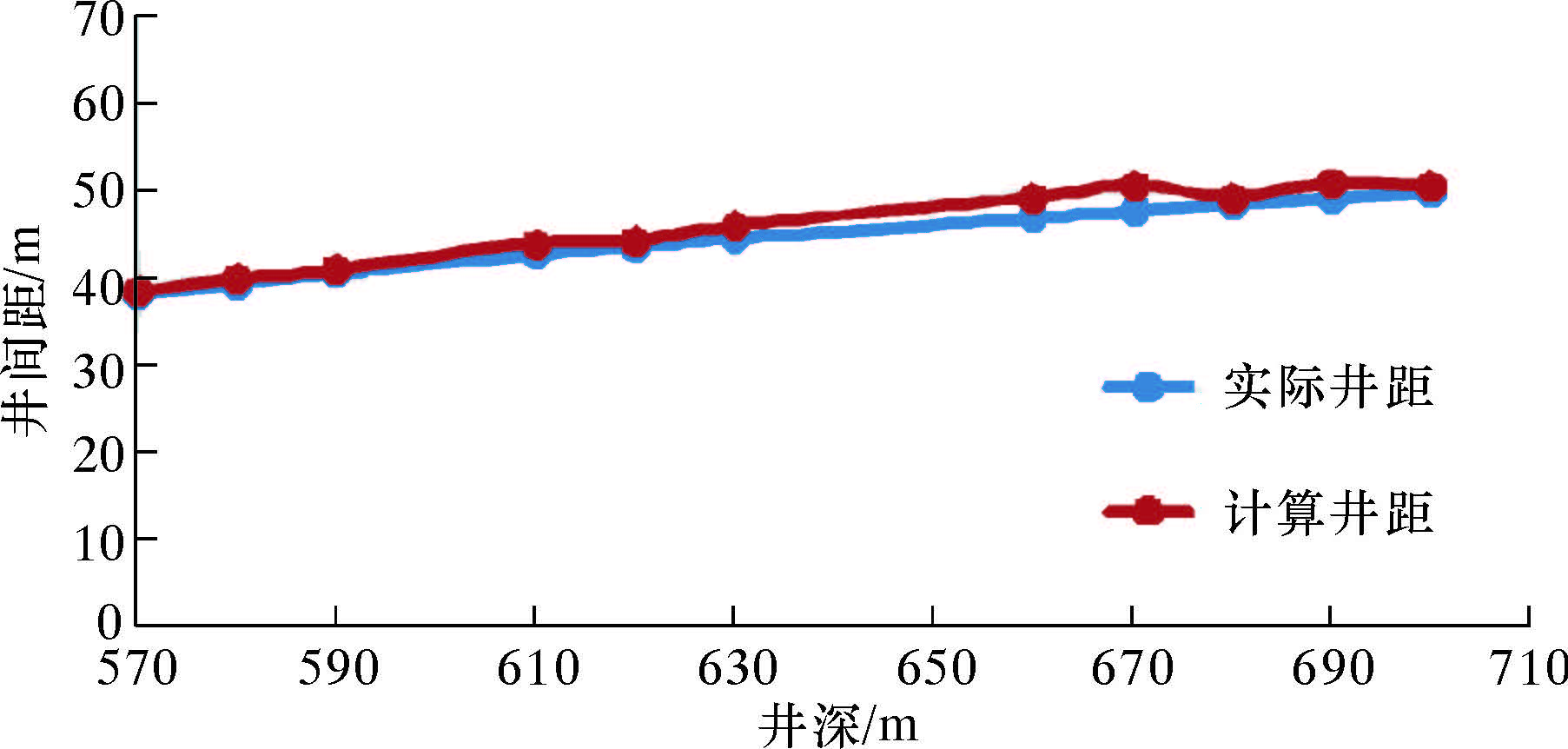
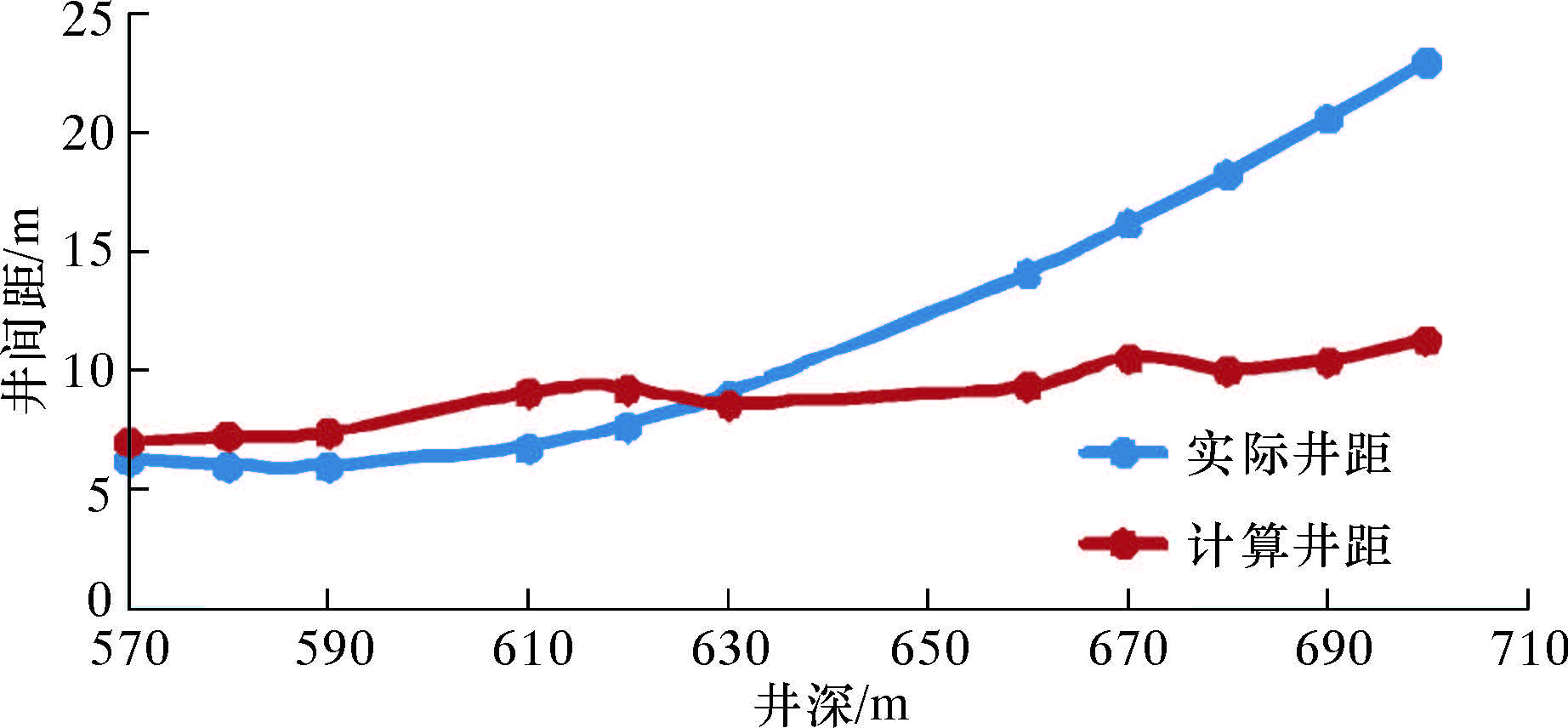
由表3和表4可知,B25井利用模型计算的井间距误差率在7%以内,B23井620 m以内计算的井间距误差率在20%左右。利用表3和表4中数据绘制风险邻井的井间距拟合曲线,结果如图8和图9所示。
|
| 图 8 B25井间距拟合曲线 Fig.8 The fitted curve of inter-well distance of Well B25 |
|
| 图 9 B23井间距拟合曲线 Fig.9 The fitted curve of inter-well distance of Well B23 |
| 井深/ m | 计算井距 差/m | 实际井 距/m | 计算井 距/m | 井距误 差/% |
| 570 | 0.14 | 6.33 | 7.04 | 10.14 |
| 580 | 0.24 | 6.08 | 7.28 | 16.50 |
| 590 | 0.14 | 6.04 | 7.42 | 18.59 |
| 610 | 1.73 | 6.87 | 9.15 | 24.93 |
| 620 | 0.22 | 7.79 | 9.37 | 16.84 |
| 630 | -0.68 | 9.06 | 8.69 | -4.24 |
| 660 | 0.69 | 14.19 | 9.38 | -51.24 |
| 670 | 1.27 | 16.22 | 10.65 | -52.25 |
| 680 | -0.53 | 18.38 | 10.13 | -81.53 |
| 690 | 0.34 | 20.68 | 10.47 | -97.54 |
| 700 | 1.00 | 23.11 | 11.47 | -101.53 |
图8基本反映了B25井的井距变化,井距的误差率较小,满足现场防碰预警要求。由图9可知,620 m以前利用模型计算的井间距具有较好的拟合效果,但整体误差比B25井稍大。这是因为B23井有3条分支井眼且在井深600 m进行侧钻,振动信号的衰减规律复杂,干扰因素较多,影响了井底振动信号的传播。
3 结 论(1)基于钻头振动波在地层和套管中的衰减规律,建立了丛式井井间距计算模型,利用套管头处接收到的特征信号可求解钻头与风险邻井的距离。
(2)利用西江某平台的监测数据,对钻头振动信号进行EMD分解,确定了钻头振动信号的特征频率为200~400 Hz,利用滤波后该频段的振动信号验证了距离计算模型具有良好的拟合效果。
(3)B25井计算的井间距误差率在7%以内,B23井620 m以内计算的井间距误差率在20%左右,满足现场防碰预警要求。B23井有3条分支井眼,振动信号的衰减规律复杂,干扰因素较多,计算的井间距误差较大,因此分支井中基于钻头振动信号的距离计算方法有待进一步研究。
| [1] | Forster L,Kreisler F.Well collision avoidance using distributed acoustic sensing:US,20100200743[P].2010. |
| [2] | Lowdon R,Farmer I.Collision avoidance system with offset wellbore vibration analysis:US,20110031016[P].2010. |
| [3] | Instanes G,Wagner H.Method for collision risk mitig-ation using intelligent non-invasive ultrasonic sensors for directional drilling:US,20110080807[P].2011. |
| [4] | 曹阳,石俊峰.一种钻井作业中的防碰绕障方法及系统:中国,102953722[P].2013-03-06. |
| [5] | 刘刚,孔得臣,孙金,等.套管头振动信号特征应用于油井防碰监测的可行性分析[J].中国海上油气,2012,24(3):54-57. |
| [6] | 刘刚,刘华亮,何保生,等.丛式井钻头距邻井井筒距离的计算模型[J].石油机械,2013,41(10):46-50. |
| [7] | 张家田.丛式钻井防碰预警系统测量模型的建立[J].西北大学学报:自然科学版,2001,31(5):418-420. |
| [8] | 黄诚惕.希尔伯特-黄变换及其应用研究[D].成都:西南交通大学,2006. |
| [9] | 李卿.EMD时频分析方法的研究与应用[D].武汉:华中师范大学,2008. |
| [10] | 于徐红.红枫湖大桥健康监测与评估系统数据处理的研究与实现[D].贵州:贵州大学,2007. |



