0 引 言
水力旋流除砂器作为一种重要的液-固非均相混合物的分离装置,由于其结构简单、使用方便、运行及维修成本低、分离性能好等优势[1, 2],在化工、发电、冶金和造纸等方面都得到广泛应用,尤其在海上油田注水工艺中产生了巨大的经济效益。
海上油田投产后,随着原油的不断采出,会导致油层压力不断下降,使油井产量降低[3]。为了保持和恢复开采后的油层压力,提高油田开采速度和采收率,必须对油田进行注水。由于海上油田水源井出砂严重,不能直接配注,水源井水要先经过水力旋流除砂器进行初步除砂再与海水混合,最后经精细过滤器过滤才能注水。水力旋流除砂器实现了对海上油田水源井水进行初步除砂处理的过程,其除砂性能的好坏直接影响后续过滤器的正常运转。
截至目前,国内外学者对旋流器已经做了很多研究。试验方面,黄素逸[4]提出的流动显形法和颜大椿[5]提出的激光测速法提供了旋流器内部流场的测定方法,但是流动显形法只能定性测量,激光测速法虽然可用性较高,但是操作繁琐,价格昂贵。数值模拟方面,F.Boysan[6]利用标准κ-ε模型对旋流器内部流场进行模拟发现,这种模型产生了附加黏度和不现实的切向速度,它不能充分模拟旋转流体;J.C.Cullivan[7, 8]及S.Schuetz[9]通过研究表明,雷诺应力RSM模型可以提高旋转流场的模拟精度;S.M.Mousavian和A.F.Najafi[10, 11]采用RSM模型、VOF模型和LES模型对气-液固三相旋流分离器的流场分布进行模拟发现,RSM模型因考虑了各向异性的强旋流特性,与试验数据吻合。对于颗粒轨迹的模拟,操波等[12]认为颗粒相体积分数小于10%时,颗粒浓度属于稀浓度范畴,可忽略颗粒间相互作用及颗粒对流体作用的影响,适合采用拉格朗日离散相模型(DPM);DPM模型计算简单,并能较好地追踪颗粒的运动[13, 14],谭慧敏等[15]运用DPM模型对导叶式旋风管排尘段二次流作用下不同粒径颗粒的运动轨迹进行了模拟,解释了排尘口处颗粒返混夹带的原因;许妍霞[16]通过DPM模型追踪粒子在旋流器中的运动轨迹,发现模拟结果与试验数值吻合。
笔者以水和砂为介质,对TP-II-250型水力旋流除砂器(旋转方向为右旋,筒体直径为250 mm)的压降、粒级效率以及除砂效率进行试验研究,并结合数值计算,运用Fluent商业软件选用RSM模型和DPM模型对水力旋流除砂器内部压力场、速度场以及固相颗粒的运动轨迹进行模拟,以期为水力旋流除砂器更好地应用于海上油田注水工艺提供依据。
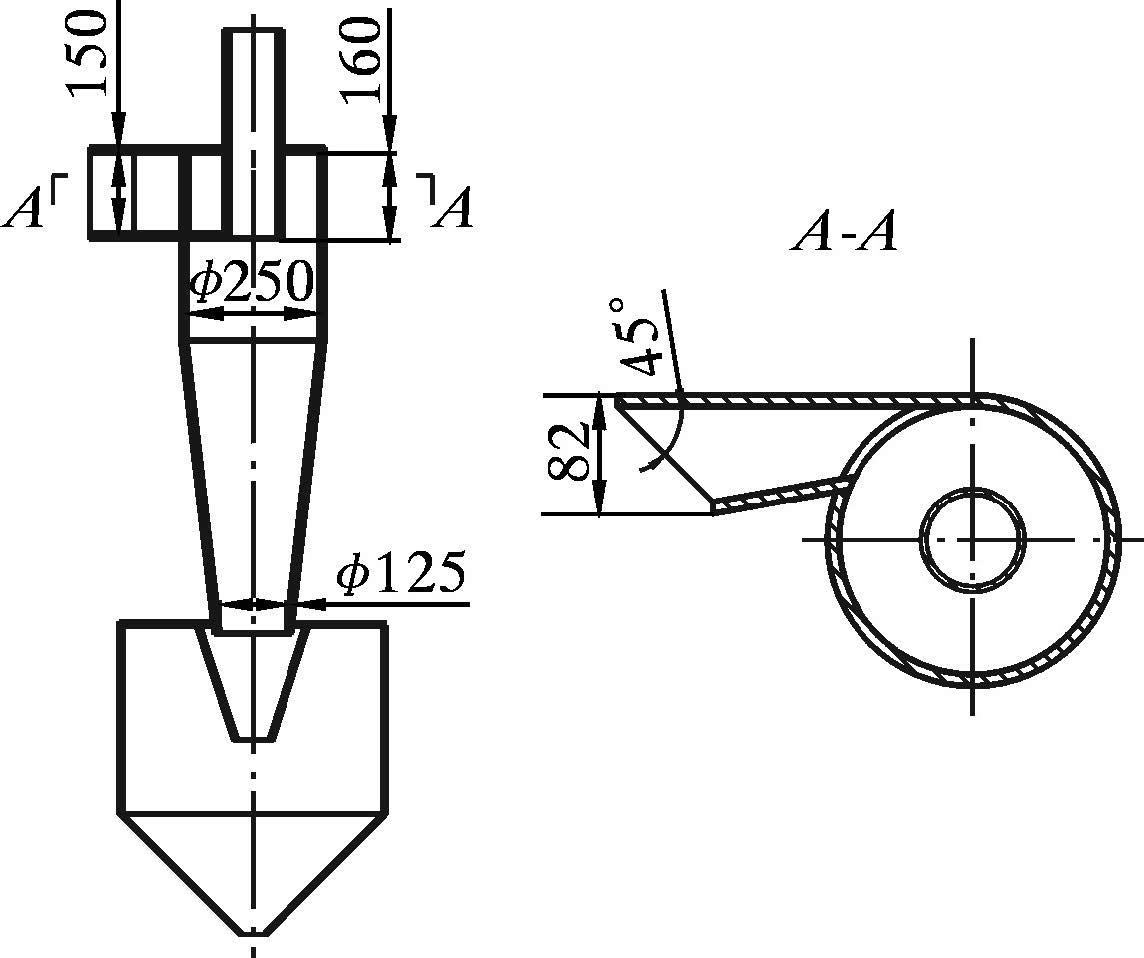
1 试验研究TP-II-250型水力旋流除砂器的结构如图 1所示。液-固两相混合物沿切向方向高速进入水力旋流除砂器后,在圆柱腔内形成高速旋转流场,因密度差而产生不同的离心力,密度较大的固相被甩至内壁,并沿内壁螺旋式向下运动,最后由底流口排入灰斗;密度较小的液相则靠近旋流器中心,螺旋上升由溢流管排出[17],从而达到液固分离的目的。
|
| 图 1 TP-II-250型水力旋流除砂器的结构简图 Fig. 1 Structure of the TP-II-250 hydrocyclone desander |
试验流程见图 2。试验装置主要由电机、水泵、电磁流量计、压力表、除砂器本体以及管线组成。

|
| 图 2 试验流程图 Fig. 2 Flow chart of the experiment 1-除砂器;2-电磁流量计;3-阀门;4-水箱;5-水泵;6-电机。 |
除砂器进液流量由电磁流量计计量,并通过调节变频器控制电机转速来改变水泵的输送流量;进、出口的压力由压力表测量;除砂效率通过对进、出口取样、过滤、称量和浓度计算来衡量,其公式如下。
进液体积Vi为:
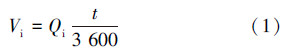
式中,Qi为进液流量,t为时间。
入口进料含砂质量浓度Ci为:

式中,mi为入口进料含砂质量。
旋流出口含砂质量浓度Co为:

式中,mo为旋流出口含砂质量,Vo为旋流出口物料体积。
除砂效率η为:

除砂器的除砂粒级效率是通过库尔特激光粒度仪分别对进出口处的固相砂颗粒进行粒度分布测量,粒度为x的颗粒分离前、后的体积分数分别记为fi(x),fo(x),则其粒级分离效率ηc(x)[18]为:
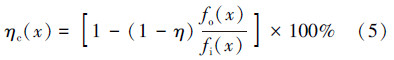
TP-II-250型水力旋流除砂器的网格划分如图 3所示。坐标原点取在圆柱腔体顶盖上截面的中轴线上,向下为正。除砂器整体采用分区划分成结构化网格,网格划分的总数为570 560。

|
| 图 3 计算模型网格划分 Fig. 3 Sketch chart of the computation grid |
数值模拟运用Fluent商业软件,利用控制体积法建立离散方程,采用经典Simple算法以及Quick差分格式求解控制方程。其中对于水力除砂器内非稳定不可压缩的液相湍流流动采用RSM模型,其输运方程为:

式中,等号左端的2项分别为雷诺应力的时间变化率和对流项;等号右端的4项分别为扩散项、压力应变项、产生项以及耗散项。
TP-II-250型水力旋流除砂器的入口进料含砂质量浓度Ci在 0.74 kg/m3左右,砂颗粒密度ρp为2 700 kg/m3,颗粒相的体积分数ε=Ci/ρp=2.74×10-4<1%,因此,该固相颗粒浓度属于稀相浓度范畴,颗粒运动情况可以采用拉格朗日离散相模型(DPM)进行模拟。颗粒动量方程如下。
轴向:

径向:
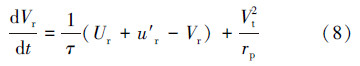
切向:

入口条件:流体为常温水,水的密度为1 000 kg/m3,动力黏度为0.357 mPa·S,入口含砂质量浓度为0.74 kg/m3。改变入口进料流量Qi分别为65、55、45、35和25 m3/h,则入口边界初始流动参数水力直径DH、入口进料速度ui、水力直径下的雷诺数ReH以及湍流强度I如表 1所示。
| Qi/(m3·h-1) | DH/mm | ui/(m·s-1) | ReH | I/% |
| 25 | 106.034 | 0.565 | 167 691.598 | 3.557 |
| 35 | 106.034 | 0.790 | 234 768.237 | 3.410 |
| 45 | 106.034 | 1.016 | 301 844.876 | 3.305 |
| 55 | 106.034 | 1.242 | 368 921.515 | 3.223 |
| 65 | 106.034 | 1.468 | 435 998.154 | 3.156 |
出口条件:出口边界设置为流动出口,为保证计算精度,溢流管长度取其内径的10倍左右,此时出口位置远离几何扰动,流动充分发展。
壁面条件:壁面采用无滑移条件,对近壁网格点采用壁面函数近似处理。
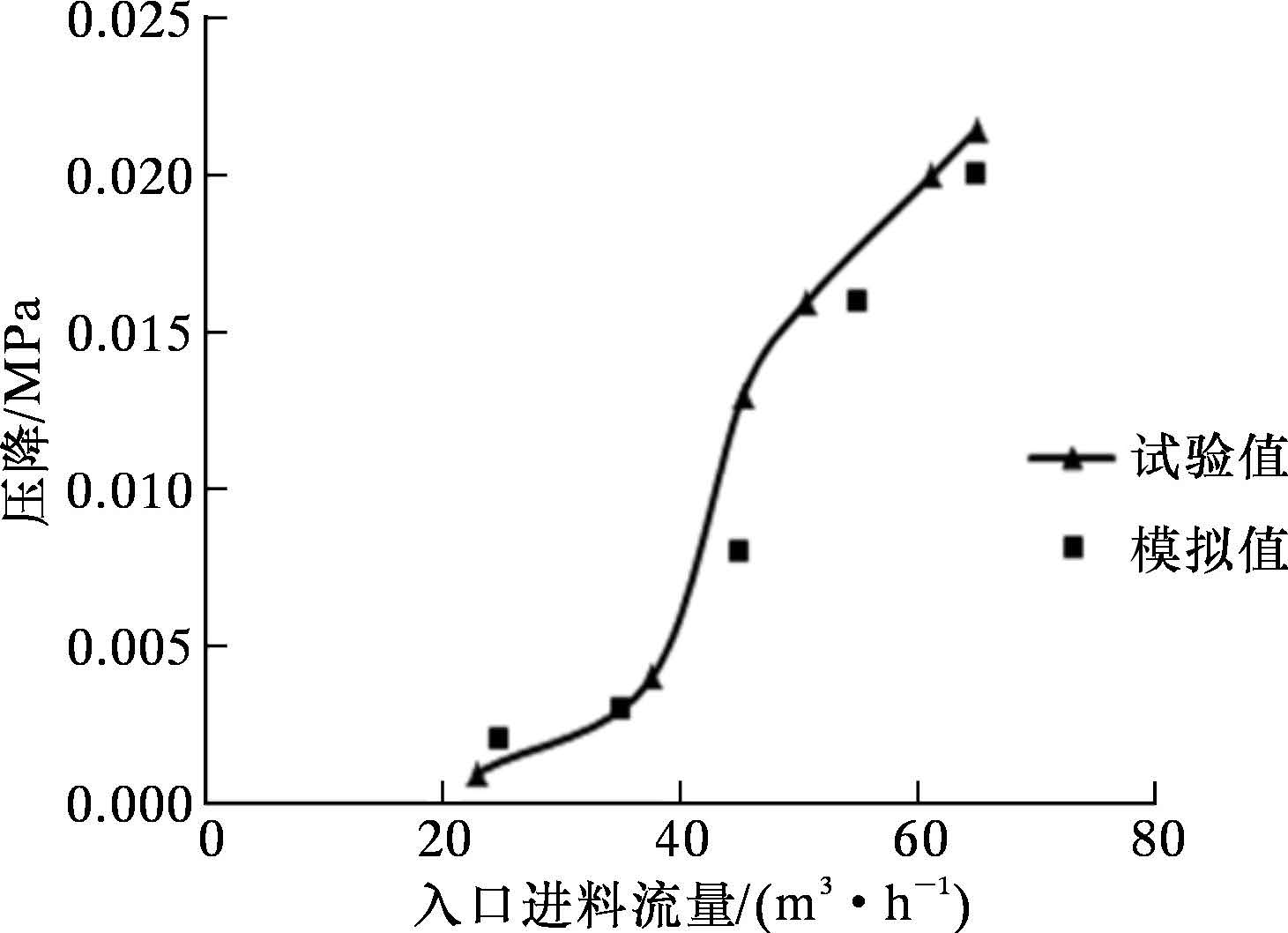
3 结果分析 3.1 液相流动 3.1.1 压力场图 4是试验压降和数值模拟压降与入口进料流量的关系比较图。从图中可以看出,压降都随着入口进料流量的增加而增加,并且模拟结果和试验结果比较接近,表明数值模拟具有较高的计算精度。
|
| 图 4 压降与入口进料流量的关系曲线 Fig. 4 Correlation between inlet flow rates and pressure drops |
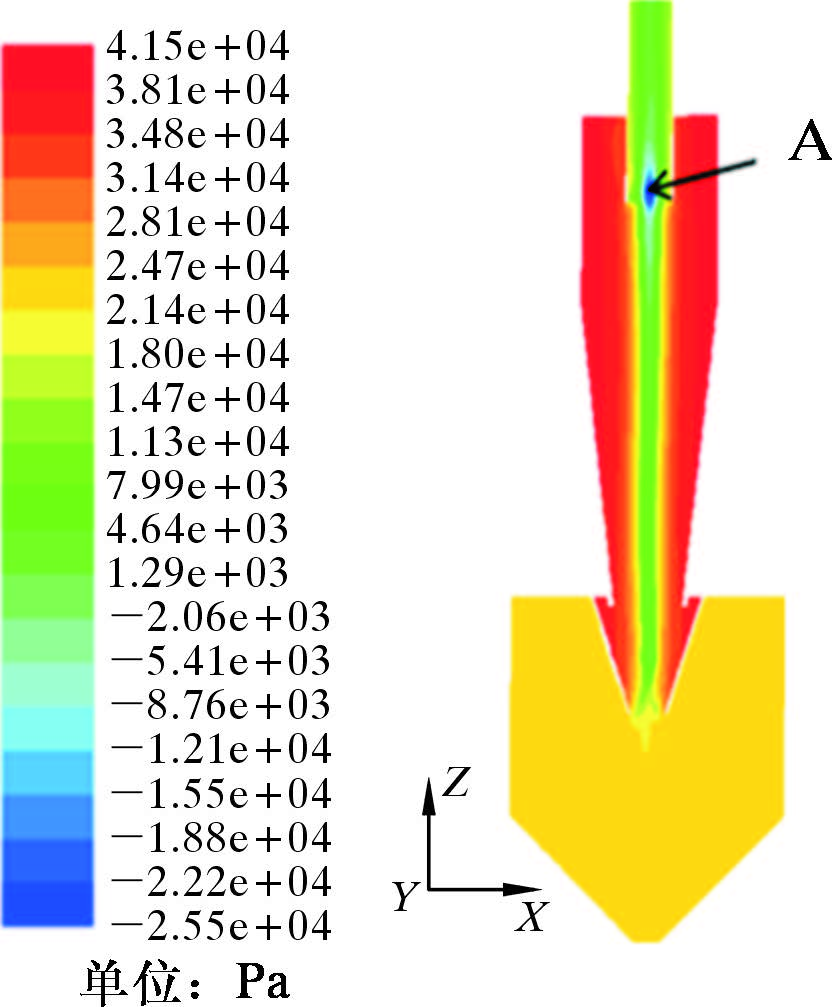
图 5是进料流量Qi=65 m3/h时,PT-II-250型水力旋流除砂器的静压分布云图。从图中可以看出,静压沿径向随半径的增大而增大,中心轴附近的静压比较小,壁面附近的静压比较高,表明在近壁面处,液相流体流动与壁面摩擦是造成水力除砂器压损的一个重要原因。除此之外,在溢流管底部中心位置处(A处)出现负压区域,说明此处的切向速度达到最大值。
|
| 图 5 静压分布云图 Fig. 5 Contour of static pressures |
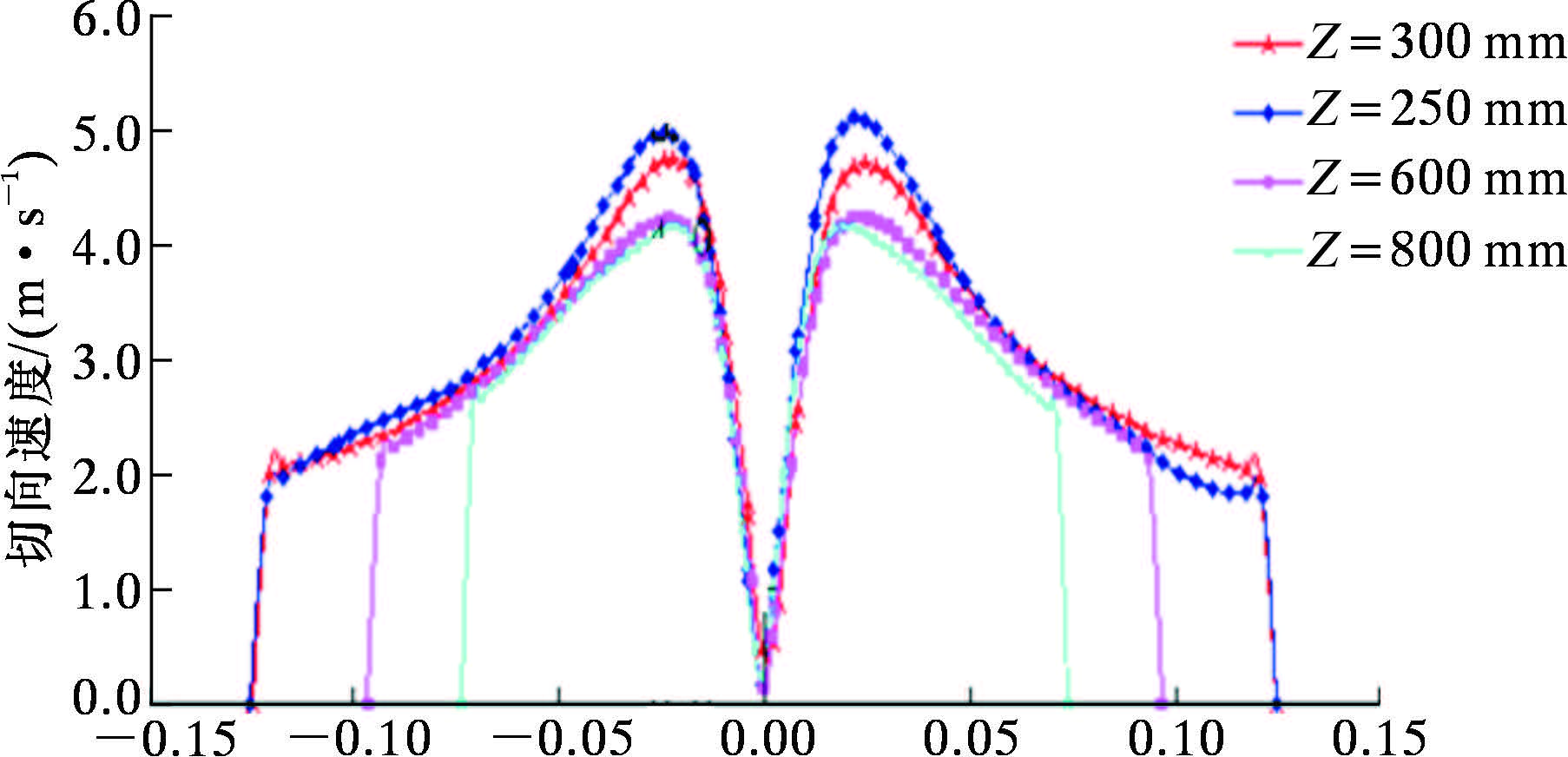
图 6和图 7分别是进料流量Qi=65 m3/h时,PT-II-250型水力旋流除砂器的切向速度分布云图和切向速度分布曲线图。从图中可以看出,切向速度沿径向呈兰金组合涡分布[19],内旋流和外旋流区域分布明显,除砂器内壁和中心区域切向速度为0。在溢流管和内壁之间构成的区域,流体流场具有不对称性,液相流体进入除砂器后,切向速度迅速增加,然后在沿着内壁旋流向下运动过程中,切线速度逐渐下降,当流体到达溢流管底部B区域后,由于和后续内旋流流体发生碰撞,则出现混流区,导致在B区域内外旋流流体切向速度迅速下降,甚至导致方向逆转随内旋流直接进入溢流管,造成短路流现象。短路流现象不仅增大了压力损失,同时也造成水力除砂器除砂效率的下降。

|
| 图 6 切向速度分布云图 Fig. 6 Contour of tangential velocities |
|
| 图 7 不同截面位置处切向速度分布曲线 Fig. 7 Distribution of tangential velocities indifferent cross sections |
图 8和图 9分别是是进料流量Qi=65 m3/h时,PT-II-250型水力旋流除砂器的轴向速度分布云图和轴向速度分布曲线图。从图中可以看出,轴向速度分布具有很好的对称性,并且呈现明显的外层流体下行、内层流体上行的双层旋转流动结构,但是内层上行流的直径比溢流管的直径略小,这很容易导致处于零速包络面(即轴向速度为0的轨迹面)处的流体被下行流夹带,直接从溢流管排出,所以可以适当减小溢流管的直径,使上行流直径略大于溢流管直径。

|
| 图 8 轴向速度分布云图 Fig. 8 Contour of axial velocities |

|
| 图 9 不同截面位置处轴向速度分布曲线 Fig. 9 Distribution of axial velocities indifferent cross sections |
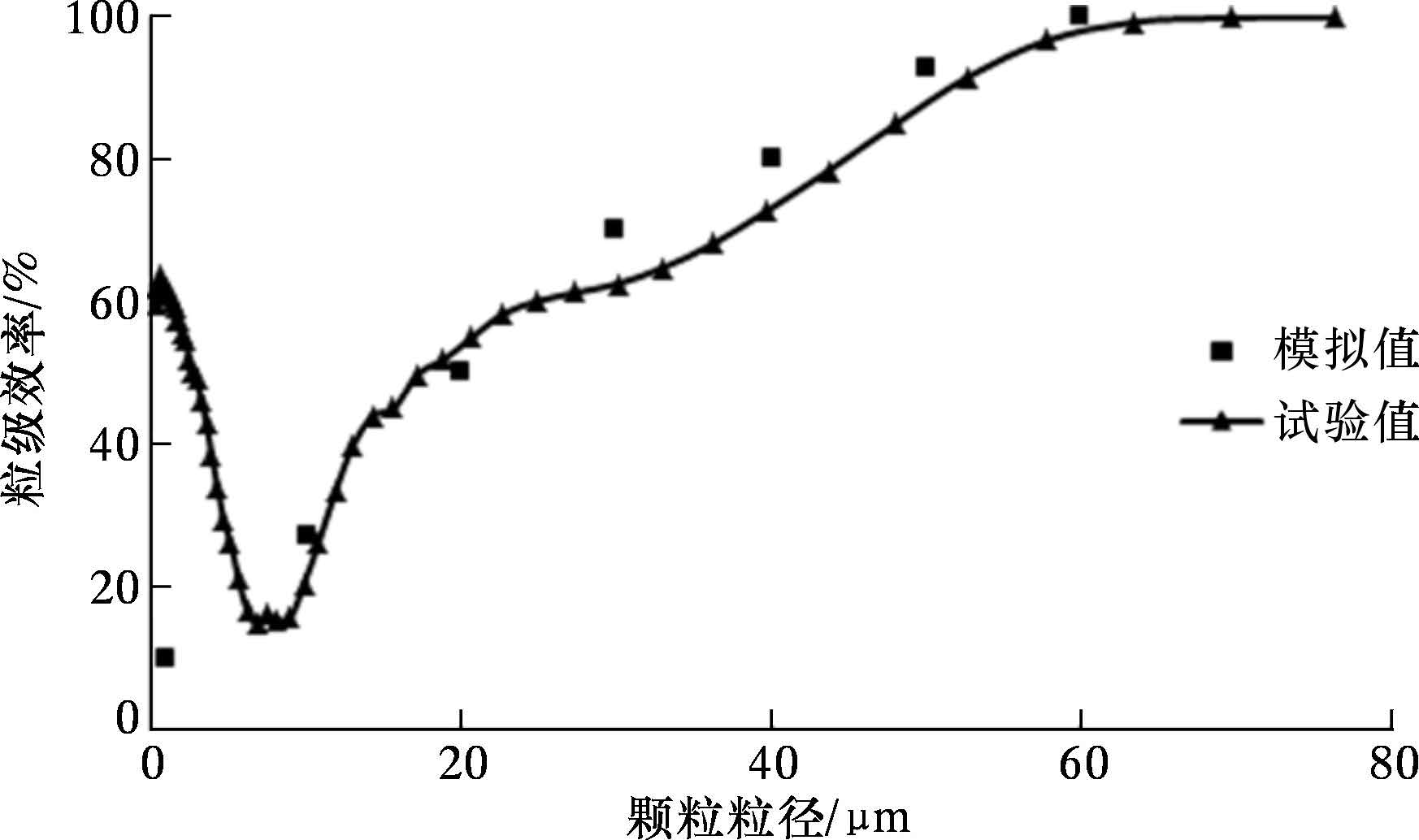
图 10是在入口进料流量为65 m3/h的条件下,TP-II-250型水力除砂器的粒级效率曲线。从整体趋势上看,模拟值与试验值比较接近,因此在水力除砂器不同区域设置不同的颗粒壁面碰撞系数,可以使数值模拟计算结果达到与实际颗粒运动情况一致的效果。但是对于一些小粒径颗粒而言,模拟值和试验值差别较大,这是因为在实际的颗粒运动中,小粒径颗粒易发生团聚或附着,所以小粒径颗粒的粒级效率也比较高。从图 10中还可以看出,此水力除砂器在本操作条件下的临界分离粒径为70 μm,基本能满足海上油田注水的预除砂处理工艺的要求。
|
| 图 10 粒级效率曲线 Fig. 10 Separation efficiencies for particles of different sizes |
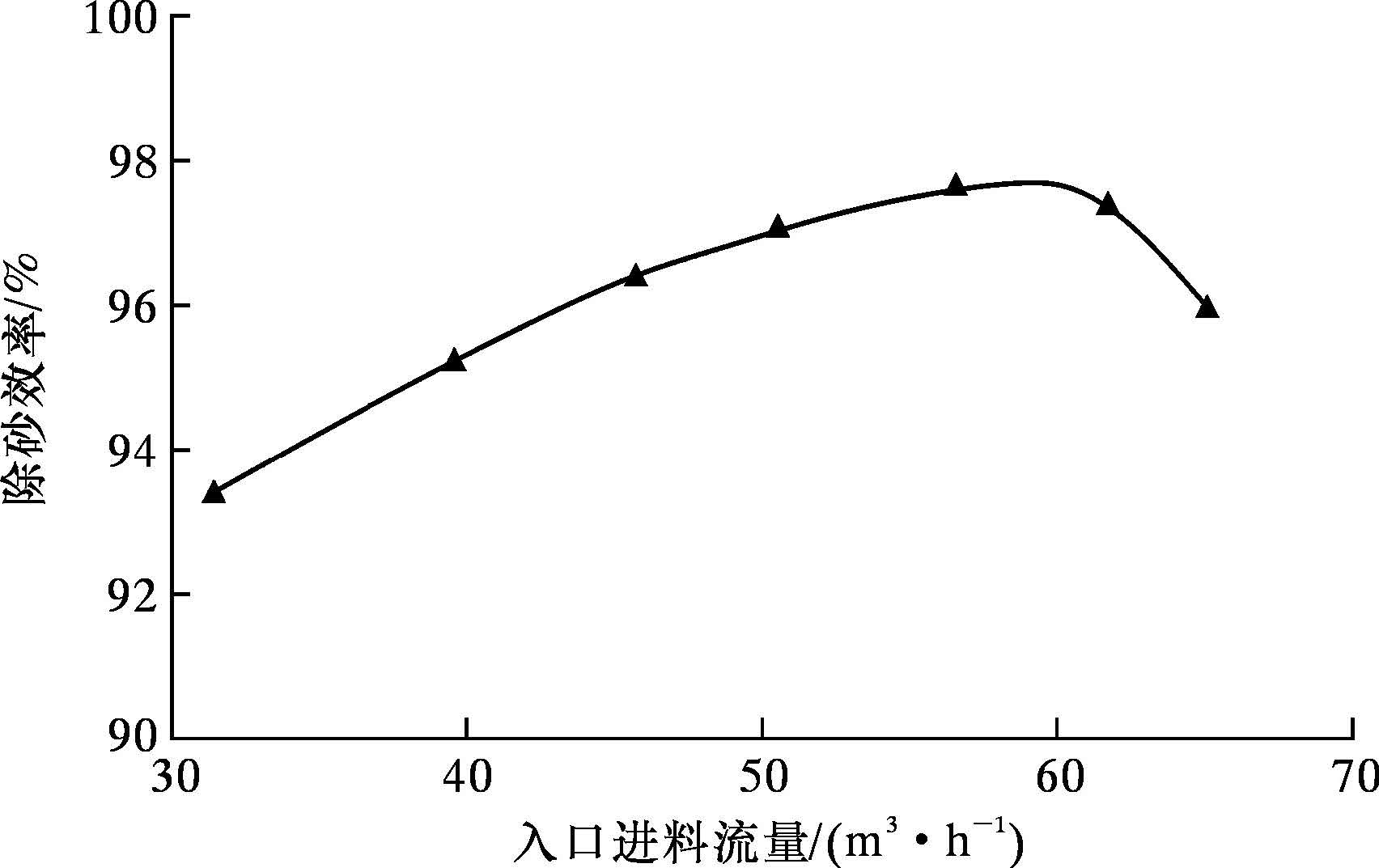
图 11所示的是在试验条件下,TP-II-250型水力旋流除砂器的除砂效率与入口进料流量的关系曲线。
从图 11中可以看出,除砂效率随入口进料流量的增加呈现先增大后减小的趋势,进料流量范围为56~62 m3/h时,除砂效率较高。随着入口流量的增加,切向速度增大,固相颗粒所受到的离心力增加,更容易被甩至器壁而分离下来;超过临界范围后,随着入口流量进一步增加,一方面,除砂器内流场的湍流强度以及颗粒所受的阻力会增加,致使离心力降低[20],另一方面,会导致颗粒的返混程度加剧,使分离效率下降。
|
| 图 11 除砂效率与流量的关系曲线 Fig. 11 Correlation between separation efficiency and flow rates |
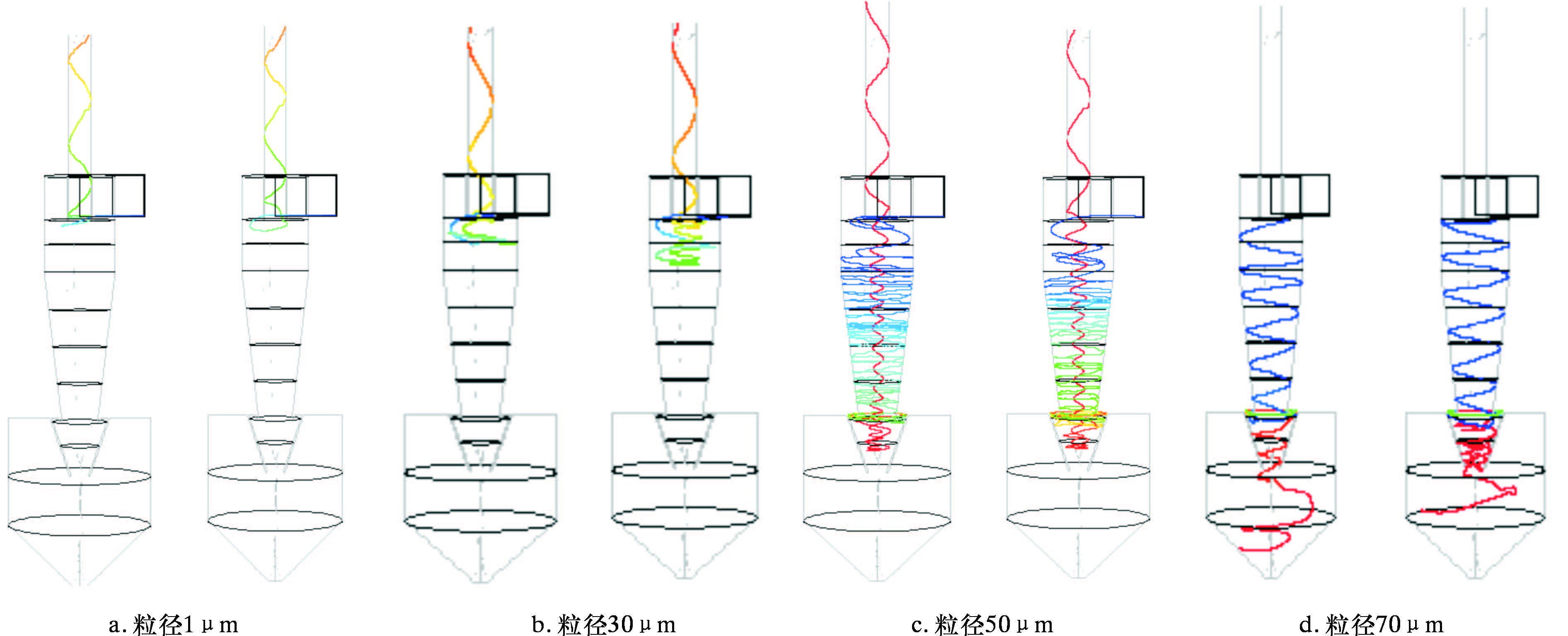
图 12是不同粒径颗粒的典型运动轨迹。从图中可以看出,不同粒径颗粒的运动规律不同,颗粒粒径越细小,越容易被中心上行流夹带逃逸;随着颗粒粒径的增大,旋流离心力也随之增大,颗粒越容易被捕集下来。
|
| 图 12 不同粒径颗粒的典型运动轨迹 Fig. 12 Typical trajectories of particles with different diameters |
(1)采用试验和数值模拟的方法对PT-II-250型水力旋流除砂器内液-固两相流动进行了研究,研究结果表明,数值模拟采用RSM模型和DPM模型模拟液-固两相流动,具有一定的计算精度。
(2)PT-II-250型水力旋流除砂器的压降随着入口进料流量的增加而增加,流体流动与壁面的摩擦以及短路流现象是造成压损的主要原因。
(3)切向速度和轴向速度是影响颗粒分离的主要流速分量,切向速度分布符合兰金组合涡特征,并且在溢流管底部区域,短路流现象明显;轴向速度分布具有很好的对称性,但是内层上行流的直径比溢流管的直径略小。
(4)不同粒径颗粒的运动轨迹不同,粒径越小,越容易逃逸,但是对于微小颗粒而言,由于分离过程中发生团聚或附着,其分离效率也比较高。
(5)除砂效率随进料流量的增加呈现先增大后减小的趋势,进料流量范围在56~62 m3/h时,除砂效率最高。
| [1] | Wang B,Yu A B.Numerical study of gas-liquid-solid flow in hydrocyclones with different configuration of vortex finder[J].Chemical Engineering Journal,2008,135(1/2):33-42. |
| [2] | Ghodrat M,Kuang S B,Yu A B,et al.Numerical analysis of hydrocyclones with different vortex finder configuration[J].Minerals Engineering,2014,63:125-138. |
| [3] | 罗国强,祝宁,高爱华.浅谈油田注水工艺技术[J].科技致富向导,2012(2):308. |
| [4] | 黄素逸.流动可视化[M].北京:科学出版社,1991. |
| [5] | 颜大椿.试验流体力学[M].北京:高等教育出版社,1992. |
| [6] | Boysan F,Ayers W H,Swithenbank J.Fundamental mathematical-modeling approach to cyclone design[J]. Transactions of the Institution of Chemical Engineers,1982,60:222-230. |
| [7] | Cullivan J C,Williams R A,Cross C R.New insights into hydrocyclone operation[J].Particulate Science and Technology,2003,21:83-103. |
| [8] | Cullivan J C,Williams R A,Dyakowski T.et al.New understanding of a hydrocyclone flow field and separation mechanism from computational fluid dynamics[J].Minerals Engineering,2004,17:651-660. |
| [9] | Schuetz S,Mayer G,Bierdel M,et al.Investigations on the flow and separation behavior of hydrocyclones using computational fluid dynamics[J].International Journal of Mineral Processing,2003,73:229-237. |
| [10] | Mousavian M S,Najafi A F.Numerical simulation of gas-liquid-solid flows in a hydro cyclone separator[J].Archive of Applied Mechanics,2009,79(5):395-405. |
| [11] | Lee J W,Yang H J,Lee D Y.Effect of the cylinder shape of a long-coned cyclone on the stable flow-field establishment[J].Powder Technology,2006,165:30-38. |
| [12] | 操波,高广德.扩散式旋风分离器气固两相流场的数值模拟[J].煤矿机械,2008,29(8):44-47. |
| [13] | 孙秀君,孙海鸥,姜任秋.油气分离器内油滴轨迹的数值模拟[J].应用科技,2006,33(10):69-72. |
| [14] | 章莉,颜彬航,吴昌宁,等.超短接触反应器气固快分装置的数值模拟[J].化工学报,2010,61(3):623-628. |
| [15] | 谭慧敏,王建军,亓成刚,等.导叶式旋风管排尘口处颗粒返混夹带现象[J].化工学报,2011,62(3):716-721. |
| [16] | 许妍霞.水力旋流分离过程数值模拟与分析[D].上海:华东理工大学,2012. |
| [17] | 吕瑞典,李君裕.除泥旋流器试验分析[J].西南石油学院学报,1995,17(2):108-113. |
| [18] | 贺杰,蒋明虎.水力旋流器[M].北京:石油工业出版社,1996:50-51. |
| [19] | 王军,陈宁.旋流器流场模拟及特性分析[J].江苏科技大学学报:自然科学版,2012,26(4):87-90. |
| [20] | 任向军,王振波,金有海.轴流式气液旋流分离器分离性能的试验研究[J].石油化工设备,2009,38(3):16-19. |




