2. 长江大学机械结构强度与振动研究所
2. Research Institute of Mechanical Structure Strength and Vibration, Yangtze University
0 引 言
随着我国油气井的使用已经逐渐达到开发应用所要求的年限,同时现有的油气田开发难度逐渐增大,为了延长老油井的使用年限,提高对新开发油气田(特别是对低渗透率油气田)的采收率,水力压裂技术逐渐成为海洋和陆地油田普遍使用的一项石油稳产、增产措施[1]。水力压裂主要是通过压裂混砂设备输出压裂混合液,通过压裂泵将高压压裂液注入到地下形成裂缝提高油气的渗透率,所以对于整套压裂技术的实施,压裂机组混砂设备性能是成功的关键。因此混砂搅拌的结构性能以及混合搅拌效果一直是国内外研究的热点[2, 3]。
文献[4, 5, 6]中根据几何以及动力相似理论,通过小型设备的模拟来研究压裂液搅拌过程的最佳操作条件,从而为实际混砂车搅拌罐获得良好的搅拌效果;文献[7, 8]中根据正交实验法,考虑了可能造成对搅拌功率以及时间影响变化较大的因素,并基于各因素间的交互作用,对搅拌罐内部混合流场进行了Fluent模拟,得到了搅拌罐的结构优化方案。针对混砂搅拌的特点,通过对混砂搅拌装置结构性能的分析,并采用Fluent软件完成对混砂搅拌装置结构内部流场数值模拟,验证了结构的可行性。研究结果可为混砂搅拌装置的设计提供指导。
1 关键结构分析搅拌叶轮和混砂罐是压裂混砂装备的关键部件,其部件相关的结构性能参数对于结构强度、搅拌效果以及搅拌时间都有较大的影响[9, 10, 11, 12],因此,有必要对搅拌叶轮和混砂罐的结构进行专门设计。
1.1 搅拌叶轮搅拌器的作用是通过电机带动搅拌叶轮对罐中固液混合物进行搅拌使混合物溶解均匀,因此搅拌叶轮是关键结构设计之一。压裂混砂车的混合液状态属于固液混合相,搅拌器的作用是将固体均匀混合到压裂液中,使所有颗粒达到悬浮状态。因此,当搅拌器的搅拌速度超过使固体悬浮的临界转速以后,继续增大搅拌速度所产生的效果很小,然而功率消耗却急剧增大,由此可见,搅拌速度应稍高于临界悬浮速度为好,通过桨叶适用条件可得搅拌速度范围一般为1.5~3.0 m/s。若确定了叶端的速度,则根据搅拌功率可相应确定搅拌叶轮直径。而在设计叶轮宽度时主要选用叶轮直径与宽度的比值可得,由于不同的使用场合以及针对不同搅拌目的,不仅需要选用不同型式叶轮,而且必须选用不同的比值,同时在搅拌所消耗的功率一定时,两者之间比值对槽内液体的运动特性有较大影响,所以折叶式叶轮比值范围一般在0.1~0.33之间。
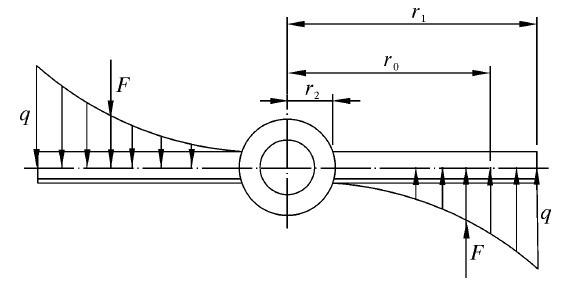
在液体搅拌过程中,高速旋转的搅拌叶轮将直接作用于罐中液体,由于压裂混合物一般具有较强的腐蚀性,同时混合物中高速流动的固体颗粒对搅拌叶轮表面的撞击,容易导致搅拌叶轮表面磨损,形成腐蚀坑,降低叶轮强度,所以对于斜桨叶的强度分析,桨叶的厚度是设计重点。由于斜桨叶受力状况复杂,要精确计算其应力状态很困难,笔者使用材料力学的方法通过分析液体对桨叶的受力情况找出危险截面。如图 1所示为叶片流体作用力沿桨叶半径方向的载荷密度变化弯矩图,通过弯矩值设计找出最大危险位置弯曲应力,以此来决定设计的相关厚度。而在计算桨叶厚度时需解决3个关键问题:一是确定计算功率;二是将计算功率分配到各层桨及各桨叶上;三是确定安全系数。在目前的结构设计中为了保证安全均按较保守的原则处理。
|
| 图 1 叶片弯矩图 Fig. 1 Bending moment of blade |
压裂混砂车的搅拌罐属于立式容器搅拌,主要由筒体和下封头组成,其搅拌装置安装于筒体的中心。对于下封头,也就是压裂混砂车搅拌槽底部,应有利于流线型流动为宜,这样可减小功率的消耗、消除混合液在底部形成停滞区和使悬浮着的固体积聚起来。下封头的尺寸根据混砂搅拌罐的容积要求选取。为了保证在高砂比砂浆或者在小砂比小砂浆的混合情况下,能完全连续地混合,防止不均匀的混合和砂浆在混合罐停留的时间较长,因此对于筒体的结构应采用罐中套罐,即在容器外侧用焊接或者法兰连接的方式装设各种形状的钢结构,使其与容器的外壁形成密闭空间。保证液体在封闭空间循环后,能与输砂器输送的砂子和各种添加剂均匀混合,在通过内腔壁的径向孔进入内腔,从而将压裂液搅拌成匀质的混合液。其筒体的具体结构设计应由筒体的承压能力决定。
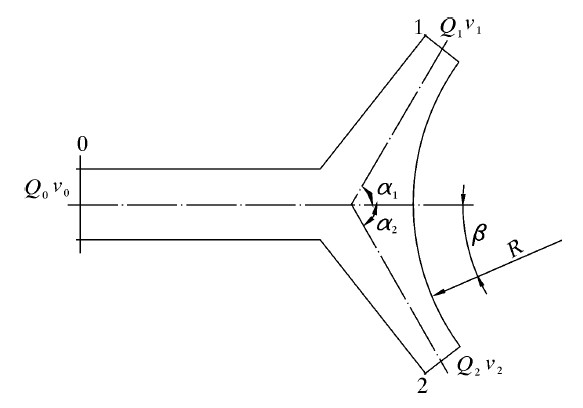
压裂混砂车的搅拌器沿容器的中心线安装,搅拌物料黏度不大,搅拌速度较高时,液体将随着桨叶旋转方向一起运动,容器中间部分的液体在离心力作用下涌向内壁面并上升,中心部分液面下降,形成打旋区,随着转速的提高,中心液面不断下降,此时外面的空气进入桨叶被吸入到液体中,液体混入气体后密度减小,降低混合效果,为了消除此现象,在容器内壁加入一定数量的竖直挡板,以阻碍液体的切向流。由于挡板的作用,流体会沿着挡板形成2股射流,射流的冲击作用,在挡板产生了作用力,作用力的大小计算如下。以速度v0向挡板射流的流体,撞击挡板后将沿挡板表面分成2股射流,速度分别为v1和v2,流量从Q0分成Q1和Q2,由于射流的冲击作用,在挡板上产生了一个反作用力R(流体作用于挡板的上的力则与之大小相等,方向相反),射流冲击挡板示意图如图 2所示。搅拌罐内挡板属于平板类型,即α=90°。设计合适的挡板厚度,可保证挡板在射流冲击力作用下满足强度要求,从而防止由于射流作用产生的侵蚀。
|
| 图 2 射流冲击挡板示意图 Fig. 2 Schematic diagram of the jetting baffle |
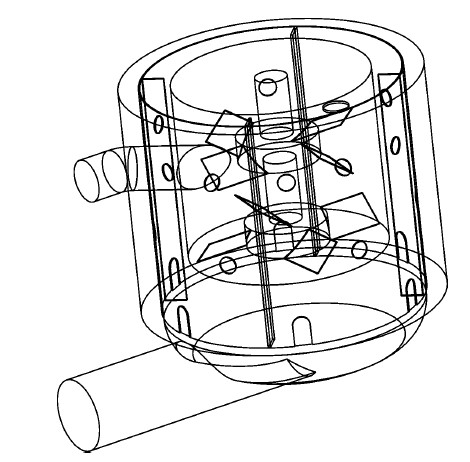
通过对混砂搅拌装置关键结构的分析,确定了混砂搅拌罐搅拌叶轮型号,设计的混砂搅拌罐内部流场分析模型如图 3所示。混砂搅拌使用的是双层夹套罐体,内、外夹套设有一定的径向入水口,采用双叶轮折叶式搅拌器,混合液介质主要从罐体入口以及罐体开口处进入,通过SolidWorks软件对搅拌装置内部流场进行建模。
|
| 图 3 搅拌罐内部流场分析模型 Fig. 3 Internal flow field analysis model of the agitator tank |
采用Workbench软件中集合的Fluent模块对罐中流场进行数值模拟,通过DesignModel模块完成对分析模型的导入,并由Mesh模块完成流场模型的网格划分,如图 4所示。设置流场边界条件,分别为inlet出口边界,outlet出口边界,axis轴向壁面,blade叶片壁面。由于流体在搅拌罐内流动,搅拌叶轮以恒定的角速度在旋转,若将参考坐标系建立在叶轮上,从这个坐标系上看,搅拌轮是静止的,而搅拌罐是转动的边界,所以在叶轮边界范围内是一个运动区域,在搅拌罐罐外为静止区域,2个域之间通过交界面进行流场的数值交换求解,因此搅拌罐流场的数值分析时建立了静止域和旋转域,同时建立静止域与选择域的交界面interface完成域之间的流场数值交换。

|
| 图 4 内部流场网格划分模型 Fig. 4 Model of internal flow field mesh |
混砂搅拌装置的搅拌运动形式决定了搅拌罐内部流场随时都处于紊流状态,因此基于Fluent软件求解器选择RNG κ-ε双方程流场分析模型。由于混合液属于多相物质混合,且水和其他混合液添加剂具有一定的速度差,所以采用Mixture模型。该模型是一种简化的多相流模型,可用于模拟两相或多相具有不同速度的流体。考虑到整个混砂液的黏度要求是0.15,如果重新考虑添加剂,这无疑增大了计算困难,所以将水的黏度设置为0.15。石英砂本来不是流体,但可以修改其物理属性,使其成为拟流体,从而可以在Fluent里面进行计算,即定义砂子密度1 500 kg/m3,颗粒直径0.000 1 mm。
2.3 边界条件的设置对于blade边界选择Moving Walk Rotational,进水口与进砂口应分别设置为velocity进口,其中进砂口的体积分数取1,出口采用pressure自由扩散的方式,旋转域置为 Moving Reference Frame,转速为250 r/min,罐体的外壁面均采用wall形式,打开压力和速度的残差计算过程,判断计算结果的收敛性。
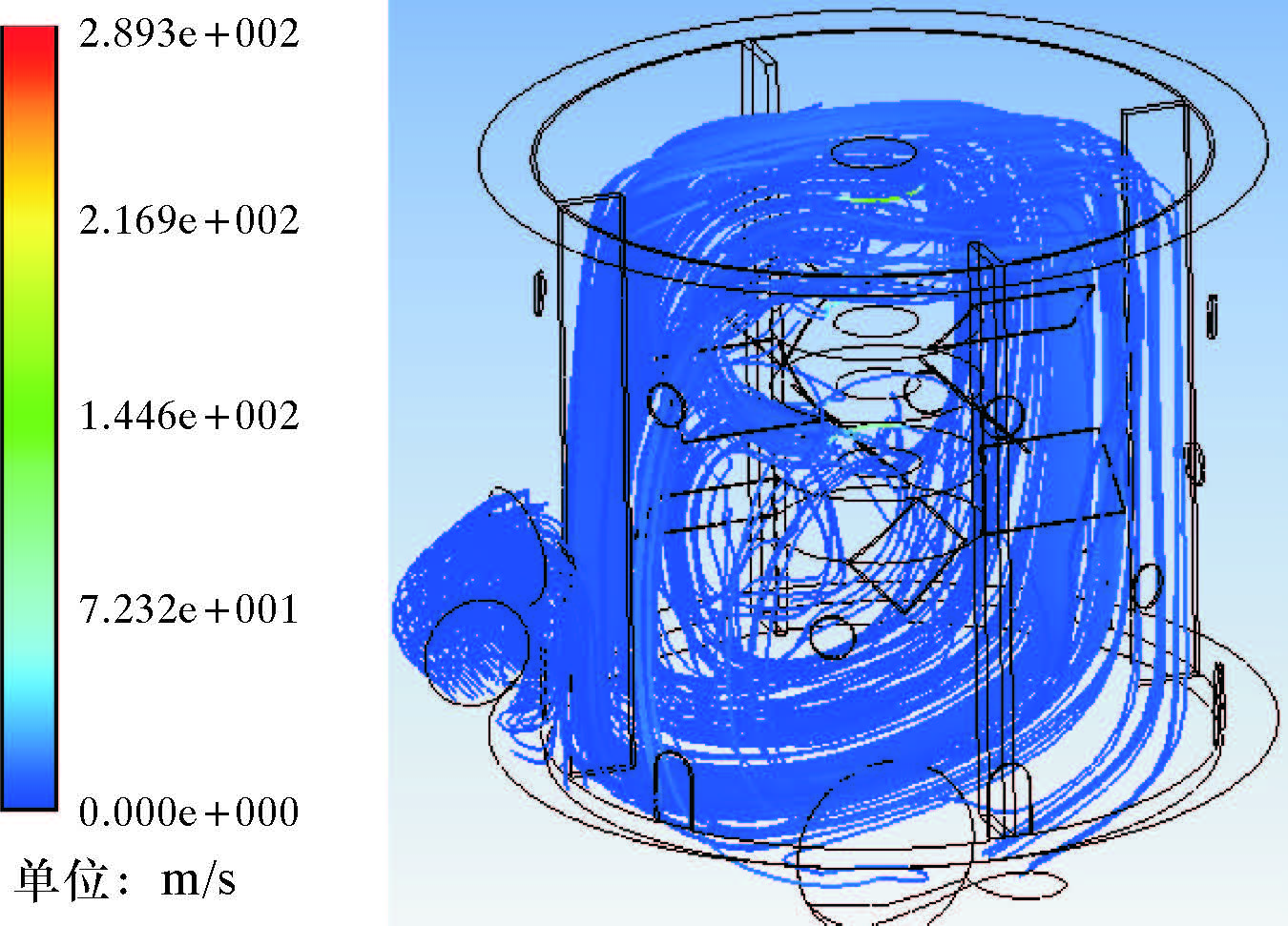
3 数值模拟结果分析对搅拌罐内部流场进行数值模拟,得到的固相体积分数为0.6的混合液在2 s时的压力云图和密度分布图。图 5为搅拌罐内流场速度流线图。图中液体从供液口进去后经过环形空间,并经罐内壁的径向口进入混合罐中,经过罐的底部、顶部和2叶轮之间搅拌罐内形成了上、下2个流场循环,可以看出这是由于上、下搅拌叶轮共同作用产生的结果,促使罐内混合液能更充分地混合均匀。
|
| 图 5 搅拌罐内流场速度流线图 Fig. 5 Velocity streamline of the flow field in agitator tank |
图 6为不同位置下的搅拌罐内压力分布云图。对比图 6a与6c可看出,下叶轮区域的压力较大于上叶轮,在罐内挡板位置处出现较大的压力,下叶轮的最大压力出现在挡板处,其值为0.15 MPa,上叶轮的最大压力出现在右侧的叶轮顶端处,其值为0.10 MPa;在图 6b中出现了低压负区,这是因为由于该位置处于上、下2流场循环区域,上、下2流体域碰撞时消耗能量,根据伯努利方程,该区域会形成低压区。

|
| 图 6 不同位置下的搅拌罐内流场压力云图 Fig. 6 Pressure distribution of the flow field in agitator tank at different locations |
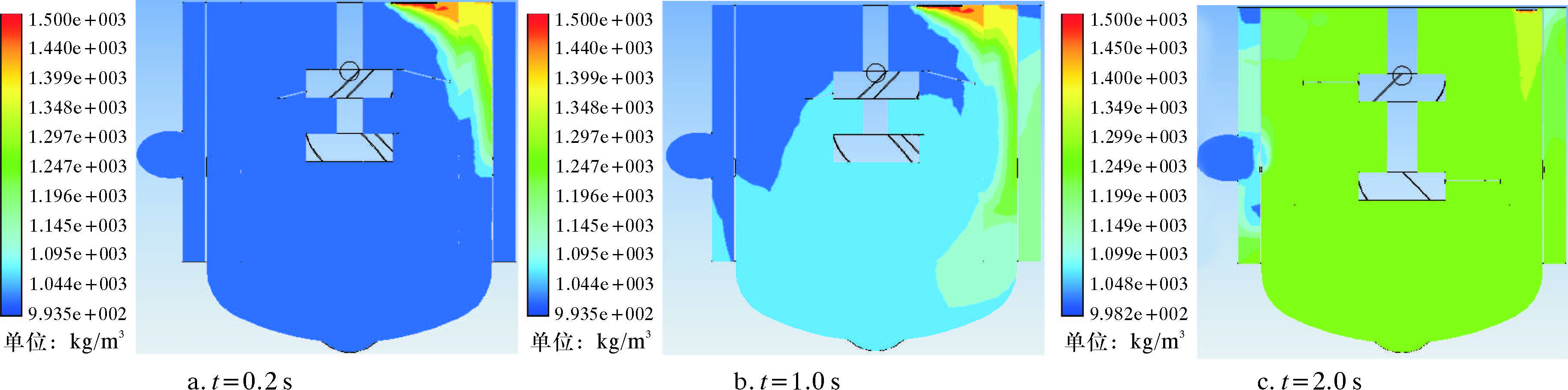
图 7为固相体积分数0.6的混合液在不同搅拌时刻的密度分布图。图 7a显示了搅拌开始时砂子由入砂口进入搅拌罐,则在入砂口的附近出混合液密度较大,当砂子逐渐增加时,搅拌罐内的密度开始逐渐增大。如图 7b所示,随着搅拌时间的增加,罐内混合液最终会趋于均匀。从图 7c可看出,除在进砂口的位置处体积分数较大,罐内其他位置处密度基本为1.299×103 kg/m3,与理论密度1.299×103 kg/m3吻合,说明固相体积分数为0.6的混合液在2.0 s内能够混合均匀,满足混砂装置设计要求。
|
| 图 7 搅拌罐不同时刻流场密度分布云图 Fig. 7 Density distribution of the flow field in agitator tank at different times |
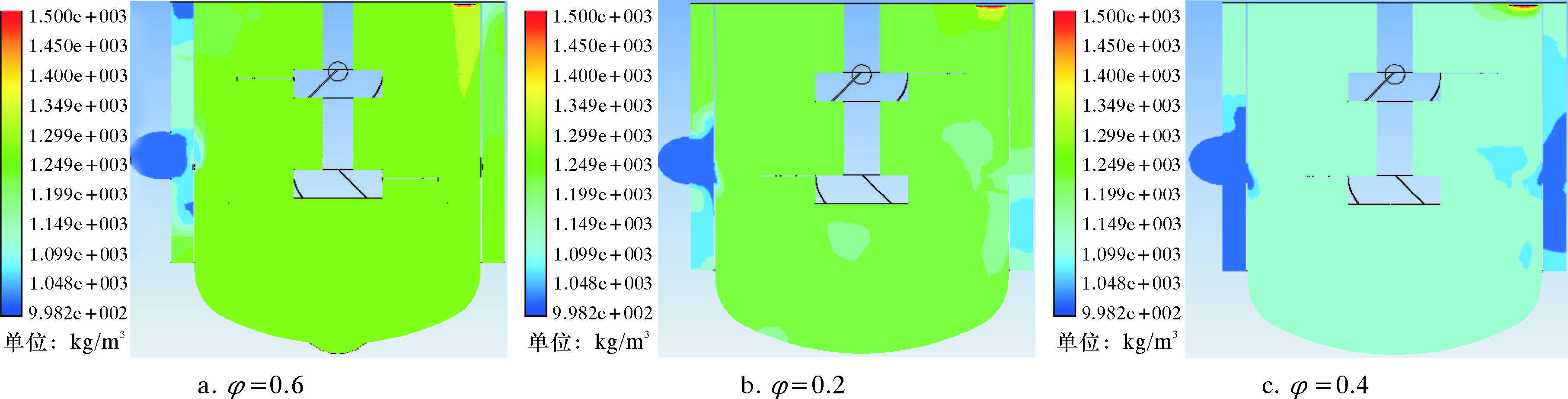
为了分析不同固相体积分数对搅拌效果的影响,笔者对搅拌罐经搅拌轴搅拌20 s后的内部密度流场进行数值模拟,结果如图 8和图 9所示。
|
| 图 8 搅拌罐纵向密度流场分布云图 Fig. 8 Longitudinal density distribution of the flow field in agitator tank |

|
| 图 9 罐底密度流场分布云图 Fig. 9 Density distribution of the flow field at the tank bottom |
进砂口的截面直径设为120 mm,则面积为0.011 3 m2,进水口的截面直径为230 mm,则面积为0.04 m2。已知出液口的排量为16 m3/min,根据质量守恒,则砂子的进口流量与水的进口流量总和应等于出液口的排量,由混合液中溶质与溶剂的体积分数比可确定水和砂的进口流量,由此可得水和砂的进口速度。因此设置不同的进口速度可改变混合液的体积分数,设计中分别取固相体积分数0.2、0.4和0.6进行模拟。
固相体积分数为0.2,即水的体积分数为80%,水进口流量Q1=16×0.8=12.8 m3/min,水进口速度v水1=5.33 m/s,砂的体积分数为20%,砂进口速度v砂1=4.72 m/s,均匀混合后理论混合密度为1 098.56 kg/m3。
固相体积分数为0.4,即水的体积分数为60%,水进口流量Q2=16×0.6=9.6 m3/min,水进口速度v水2=4.00 m/s,砂的体积分数为60%,砂进口速度为v砂2=9.44 m/s,均匀混合后理论混合密度为1 198.92 kg/m3。
固相体积分数为0.6,即水的体积分数为40%,水进口流量Q3=16×0.4=6.4 m3/min,水进口速度v水3=2.67 m/s,砂的体积分数为60%,砂进口速度为v砂3=2.67 m/s,均匀混合后理论混合密度为1 299.28 kg/m3。
由图 8可以看出,在搅拌20 s后固相体积分数为0.6、0.4和0.2的混合液密度基本分别分布在1.299×103、1.198×103和1.098×103 kg/m3左右,与理论值比较相近,说明罐内混合液混合比较均匀,但在径向进水口的位置密度较小,在进砂口的位置密度较大。比较图 9可知,在底部进水口的位置密度偏小,由于不同固相体积分数的混合液砂子沉降速度不一样,固相体积分数为0.6的混合液搅拌罐底部密度大部分区域较理论值偏小,说明此时的砂降速度较小,底部混合不充分,而固相体积分数为0.4和0.2的混合液搅拌罐底部较大部分区域的密度与理论值偏大,此时的砂降速度较大,底部混合不均匀。因此,研究不同固相体积分数的混合液砂降速度对搅拌效果的影响有一定的指导意义。
4 结 论(1)针对混砂搅拌的结构特点及对压裂混合液质量要求,基于搅拌结构强度、搅拌效果以及搅拌时间因素考虑,阐述了搅拌叶轮及搅拌罐结构设计方法,可为混砂搅拌设备设计提供一定的理论指导。
(2)基于CFD模拟技术对压裂混砂车搅拌罐中的流体进行流场的数值模拟,发现在搅拌罐内形成了上、下2个流场循环,并在2个流场的交汇处形成了低压区;通过罐中混合物密度云图发现数值分析结果与理论分析结果比较接近,说明数值分析具有一定准确性。
(3)对3种不同固相体积分数的混合液砂降速度进行分析,固相体积分数为60%的混合液砂降速度小,容易造成底部混合不充分,固相体积分数较小的混合液砂降速度较大,容易造成底部混合不均匀。
| [1] | 邓斌奇,陈浩.混砂车的发展趋势研究[J].中国石油和化工标准与质量,2011,31(7):193. |
| [2] | 胡博仲,兰中孝.大庆油田水力压裂工程[M].北京:石油工业出版社,2008. |
| [3] | 谢永金,曹立明.新型不压井作业设备的研究[J].石油机械,2007,35(9):161-164. |
| [4] | Eisinger F L.Acoustic fatigue of impellers of rotating machinery[J].J Press Vessel Technol,2002,124(2):154-160. |
| [5] | Tamburini A,Cipollina A,Micale G,et al.Dense solid-liquid off-bottom suspension dynamics:Simulation and experiment[J].Chem.Eng.Res.Design,2009,87(4):587-597. |
| [6] | Murthy B N,Deshmukh N A,Patwardhan A W,et al. Hollow self-inducing impellers:Flow visualization and CFD simulation[J].Chem.Eng.Sci.,2007,62(14):3839-3848. |
| [7] | 袁新梅,周思柱,黄天成,等.基于Fluent的大排量混砂车搅拌罐结构优化[J].制造业自动化,2014,36(4):150-156. |
| [8] | 周思柱,刘奔,华剑,等.基于均匀设计的混砂车搅拌桨结构改进[J].机械设计与制造,2013(5):120-122. |
| [9] | 周思柱,袁新梅,黄天成,等.混砂车搅拌罐实验模型相似设计及数值模拟[J].中国科技论文,2014,9(5):616-619. |
| [10] | 周思柱,陈翔,吴汉川,等.混砂车搅拌罐流场分析方法[J].石油机械,2011,39(增刊1):23-24. |
| [11] | 肖洋轶,石万凯,刘敬,等.混砂车搅拌罐内混合过程的数值模拟[J].长安大学学报:自然科学版,2014,34(2):120-126. |
| [12] | 万正洲,华剑,殷瑱,等.混砂车搅拌罐流场和功率的数值模拟[J].石油机械,2014,42(2):80-83. |



