0 引 言
目前全球使用量最大的自升式钻井平台,采用齿形楔块式锁紧系统。这种锁紧系统具有锁紧速度快、同步对中性好、结构简单以及安全可靠等优点,被广泛用于自升式钻井平台。国内外对钻井平台齿轮齿条升降系统的稳定性研究较多[1],基于ADMAS的仿真分析得到的齿轮齿条传动机构动力学特性具有有效性[2],X.M.Tan等[3]利用数值分析法研究了结构动力学,但对于钻井平台锁紧系统的力学行为分析相对较少。鉴于此,笔者结合91.4 m(300 ft)自升式钻井平台锁紧系统,对自升式钻井平台锁紧单元进行了设计,对锁紧系统进行了力学分析,以期为齿形楔块式锁紧系统设计提供方法和依据。
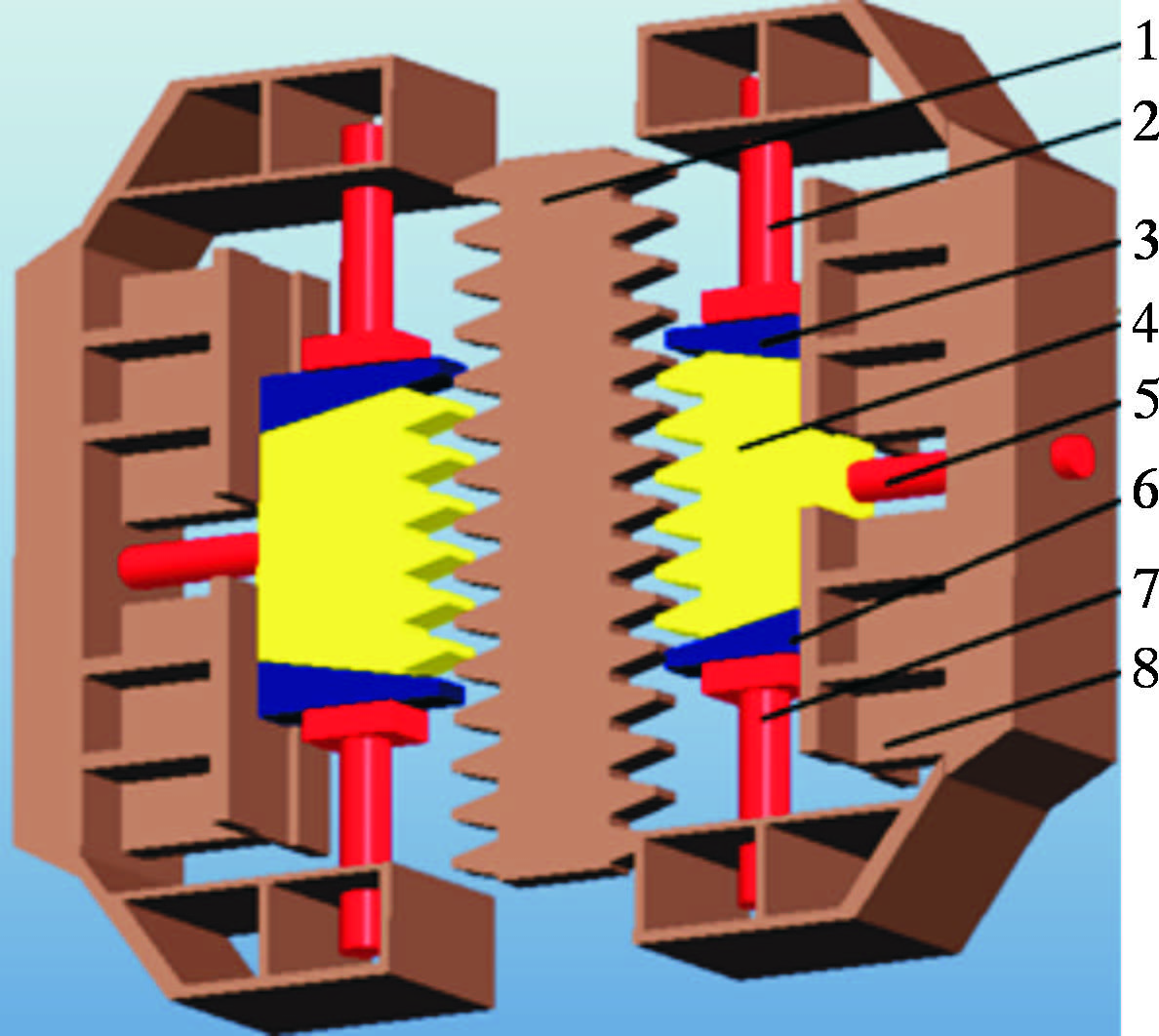
1 蜗轮蜗杆驱动的齿形楔块锁紧方案齿形楔块式锁紧系统结构如图 1所示。该齿形楔块式锁紧系统采用上、下螺杆、楔形压块、六齿锁紧块布局,锁紧齿条采用6个锁紧齿,最大限度降低主齿条的单齿载荷。锁紧齿条使用高强度钢锻造毛坯制造,通过热处理控制材料屈服强度,有很高的强度及低温韧性。利用楔形块的特点,同时从垂直和水平方向约束锁紧齿条[4]。锁紧时,操作下部螺杆总成调整锁紧齿的高度,利用侧推油缸将锁紧齿条推进桩腿齿条并啮合良好,操作顶部液压马达带动螺杆下行,从而推动上楔块下行,压住锁紧齿条。操作下部液压马达带动螺杆上行,从而推动下楔块上行,压住锁紧齿条。操作液压系统卸载,使平台重力载荷转移到上螺杆总成上,这条桩腿的载荷全部由锁紧装置承接。
|
| 图 1 齿形楔块式锁紧系统图 Fig. 1 Tooth-shape wedge-type locking system 1-桩腿齿条;2-上螺杆;3-上三角块;4-锁紧齿块;5-液压缸;6-下三角块;7-下螺杆;8-壳体。 |
在蜗轮蜗杆传动中[5],传动比可达300。若只传递运动,传动比可达1 000,传动比大,结构紧凑。当蜗杆的螺旋线升角小于啮合面的当量摩擦角时,即导程角小于3.5°,蜗杆传动具有自锁性。由于蜗杆齿是连续不断的螺旋齿,与蜗轮齿逐渐进入啮合,逐渐退出啮合,啮合齿数较多,故冲击载荷小,传动平稳,这点对于平台锁紧至关重要。
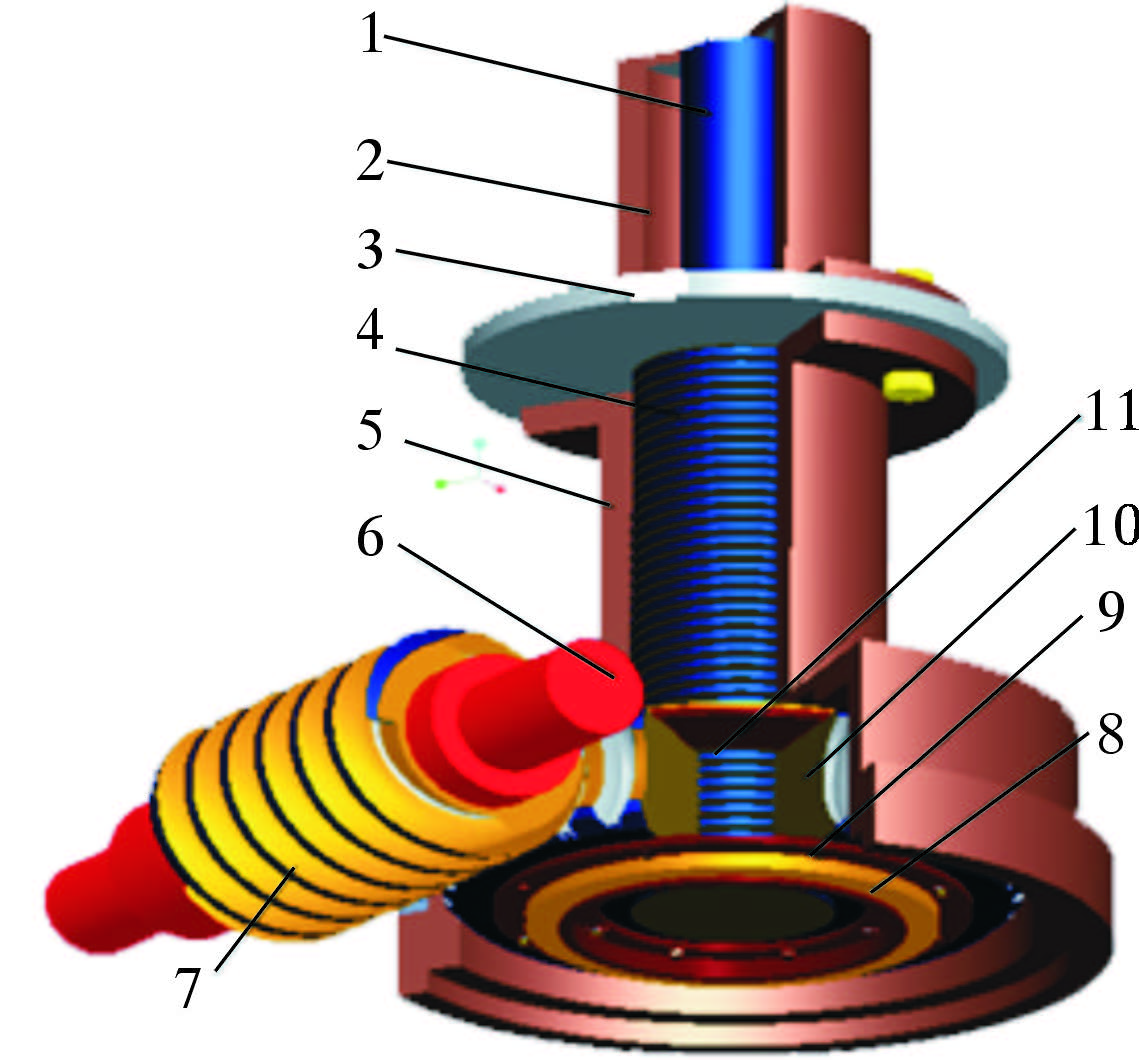
设计的异形蜗轮蜗杆结构具有传力螺旋、传导螺旋和调整螺旋等3种螺旋特点[5],如图 2所示。选用阿基米德蜗杆(即ZA蜗杆)传动,让蜗轮内圈攻螺纹,用于和螺杆螺旋配合传动。螺杆和蜗轮内圈螺纹配合,通过蜗轮旋转带动螺杆旋转,从而带动螺杆向下运动,螺杆压紧斜三角块,达到锁紧目的。这种螺旋结构简单,制造容易,间歇性工作,时间较短,并且易于自锁。
|
| 图 2 蜗轮蜗杆锁紧系统单元图 Fig. 2 Worm and worm wheel locking system unit 1—导杆;2—上壳体;3—平台甲板;4—螺杆;5—下壳体;6—蜗杆轴;7—蜗杆;8—轴承;9—下压盖;10—蜗轮;11—上压盖。 |
上、下螺杆及楔块作为承载的主要部件,选用高强度合金结构钢。蜗杆用35GrMo钢并且表面淬火处理,蜗轮轮缘选用ZCuSn10P1金属,蜗轮轮心用灰铸铁HT100铸造。其中承载部件的螺母采用高强度铜合金制造。螺杆的伸缩通过JM22-DO.063径向柱塞液压马达驱动螺母旋转产生,蜗轮与螺母为一体设计,具有质量轻、扭矩大、结构简单、性能可靠以及传动效率稳定等优点。系统采用液压动力驱动完成平台的载荷转移、锁紧和解锁操作。
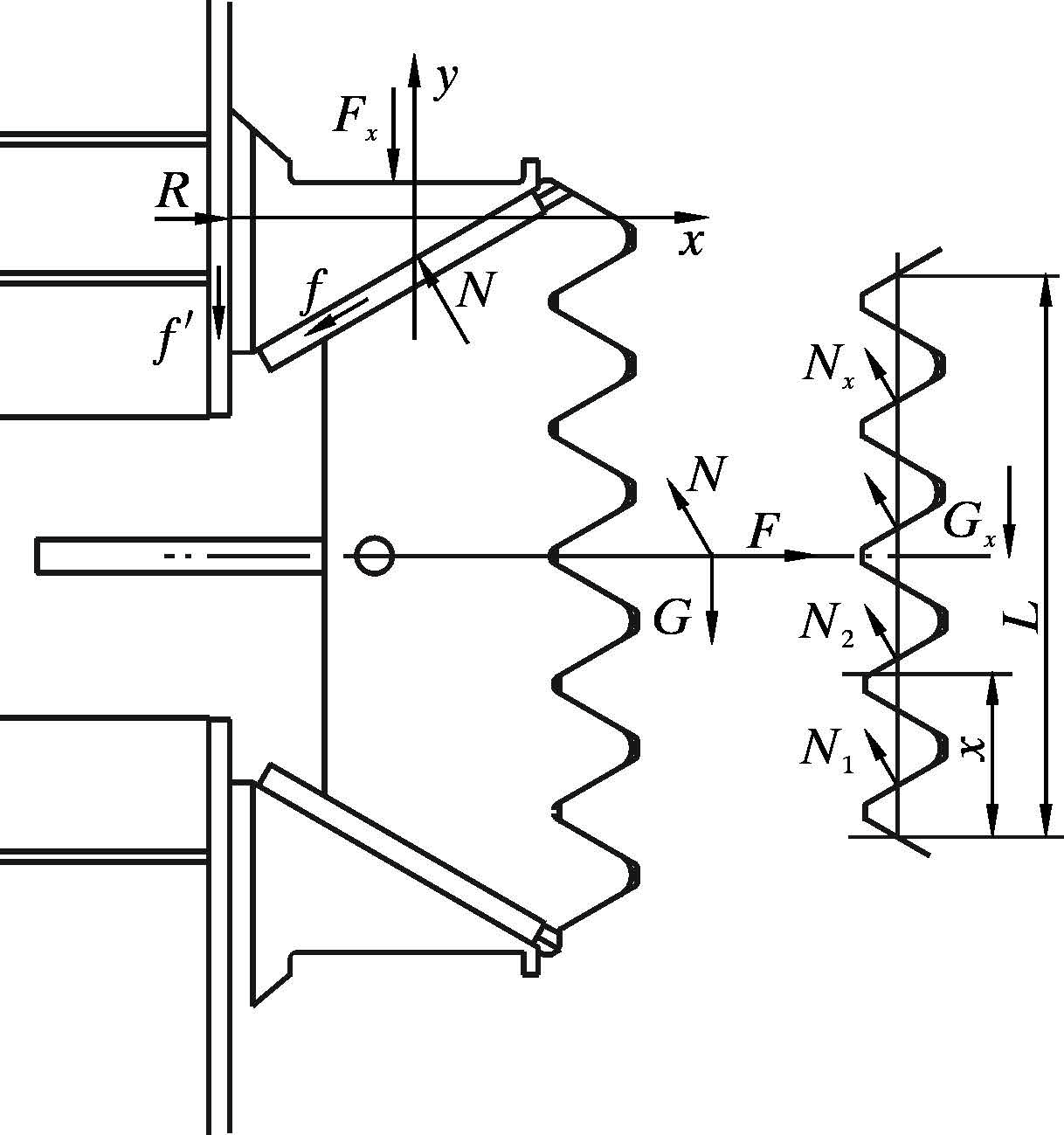
2 锁紧齿条块力学分析 2.1 锁紧齿条块受力分析该自升式钻井平台所对应的锁紧系统平台载荷9.0×104 kN。因结构对称布置,现取单根支腿齿条进行分析[6, 7]。以齿条锁紧块为受力对象,受力分析如图 3所示。
|
| 图 3 齿形楔块受力分析图 Fig. 3 Force analysis on the tooth-shape wedge block |
以上斜三角块为受力对象。图 3中R为三角楔形块支反力,Fx为螺杆向下压力,f为沿斜面摩擦力,f ′为竖直方向摩擦力。
以锁紧齿条块为研究对象进行受力分析。其中,G为平台的重力,在重力载荷作用下,P为啮合齿数,G(x)为离散到第n个齿的重力。N为每个齿面向上的力,在x位置处,垂直于锁紧齿条截面下方的力为N1,垂直于锁紧齿条截面上方的力为N2,将每根锁紧齿条上分担的竖直载荷简化为集中力,则有:
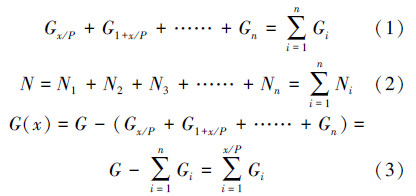
对N(x)关于位移坐标求导,令其导数为q(x),则有:
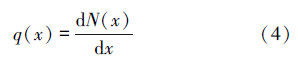
定义q(x)是齿条单位啮合长度方向上的轴向力。在长度为L的齿条上,受力如下:
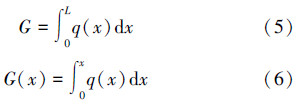
分析其中任意一个齿上的轴向力如下:
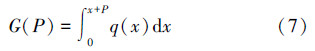
定义p(x)是锁紧齿条在单位面积侧面的法向作用力。B为齿条厚度,H为齿高。
由几何关系可得:
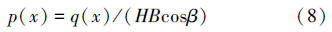
以锁紧齿条块为研究对象,三角块倾斜角α=30°,齿条压力角β=θ=60°,其中摩擦因数μ=0.15,φ为达到自锁要求的最小角,φ=arctanμ=8.35°。由静平衡得:
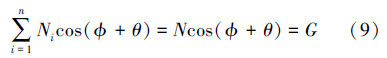
解得 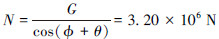 。
。
以上斜三角块为受力对象,取最大静摩擦力接近于滑动摩擦力,即f ′=μR,f=μN,可得汇交力系矩阵形式如下:
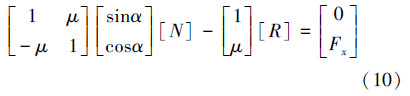
求得解析解为Fx=2×106 N。
至此,整个锁紧系统稳定后,平台载荷全部转化成蜗杆竖直向下压力。
2.2 锁紧齿条块变形分析在外力作用下,齿条齿牙会发生弯曲剪切和错位等。由于变形量微小,为弹性变形,对模型做以下假设[8]:①齿条块质量分布均匀;②齿条块内部连续;③齿条完全发生弹性变形,解锁后,可以恢复形变;④齿条块所受弹力在各个方向都相同;⑤齿条变形属于微小变形。由变形协调条件得:
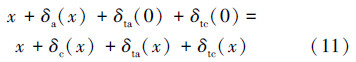
整理得:
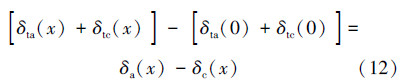
式中,δc为齿形楔块变形量,δtc为齿形楔块总变形量,δa为桩腿齿条变形量,δta为桩腿齿条总变形量。
则有:
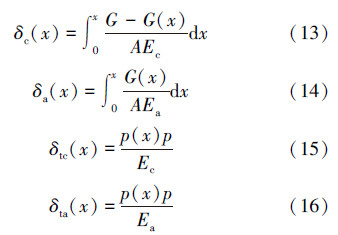
式中,A为齿条横截面面积,Ec为齿形楔块的弹性模量,Ea为桩腿齿条的弹性模量,p为齿条节距,分别带入变形协调方程得:
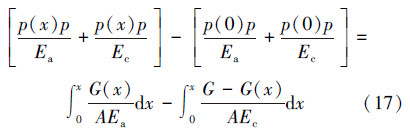
带入式(8)得:
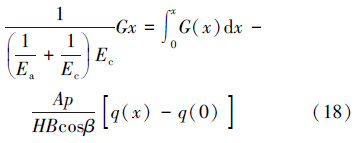
设η为 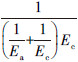 ,ω为
,ω为 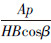 ,可得:
,可得:
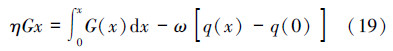
对上式两边求导,得:
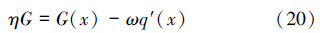
带入 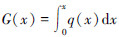 ,得:
,得:
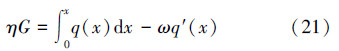
再对上式求导,得到在承受载荷前提下,轴向力分布强度的变形协调微分方程:
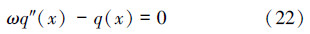
化成标准形式为:
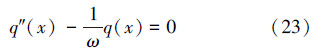
解得:
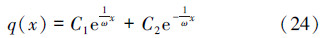
其中,C1、C2为求通解的系数。
带入初始条件x=0,G(0)=0,q′(0)= 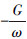 ;x=L,G(L)=G,q′(L)=
;x=L,G(L)=G,q′(L)= 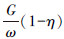 ,解得:
,解得:
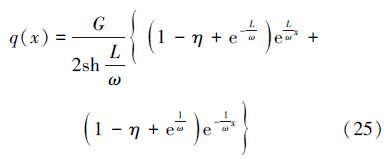
即
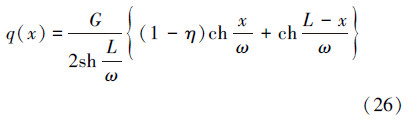
式(26)说明,变形量是关于x的双余弦函数,呈指数增长,在上部变形量达到最大。
3 锁紧系统有限元分析利用Pro/E建模,然后导入ANSYS软件进行应力分析。平台桩腿齿条的基本参数为:齿形楔块的齿数Z=6,模数m=95 mm,分度圆压力角α=30°,齿轮齿廓曲线为渐开线,齿条为直线。材料牌号为ASTM A517 GRQ,屈服极限为690 MPa,抗拉强度为790/930 MPa,泊松比为0.3,桩腿长度167.0 m。在齿形楔块接触时,设置接触类型为面接触,并且取齿接触的位置。选用(Hex Dominant)六面体主导网格划分单元[9, 10, 11],以提高计算精度。对接触位置及其周围的网格设置较为细密,其他部位较为稀松,网格划分如图 4所示。锁紧稳定后,设置约束,代入2.1节计算所得的蜗杆轴向压力。
|
| 图 4 齿形楔块网格划分图 Fig. 4 Mesh generation of the tooth-shape wedge block |
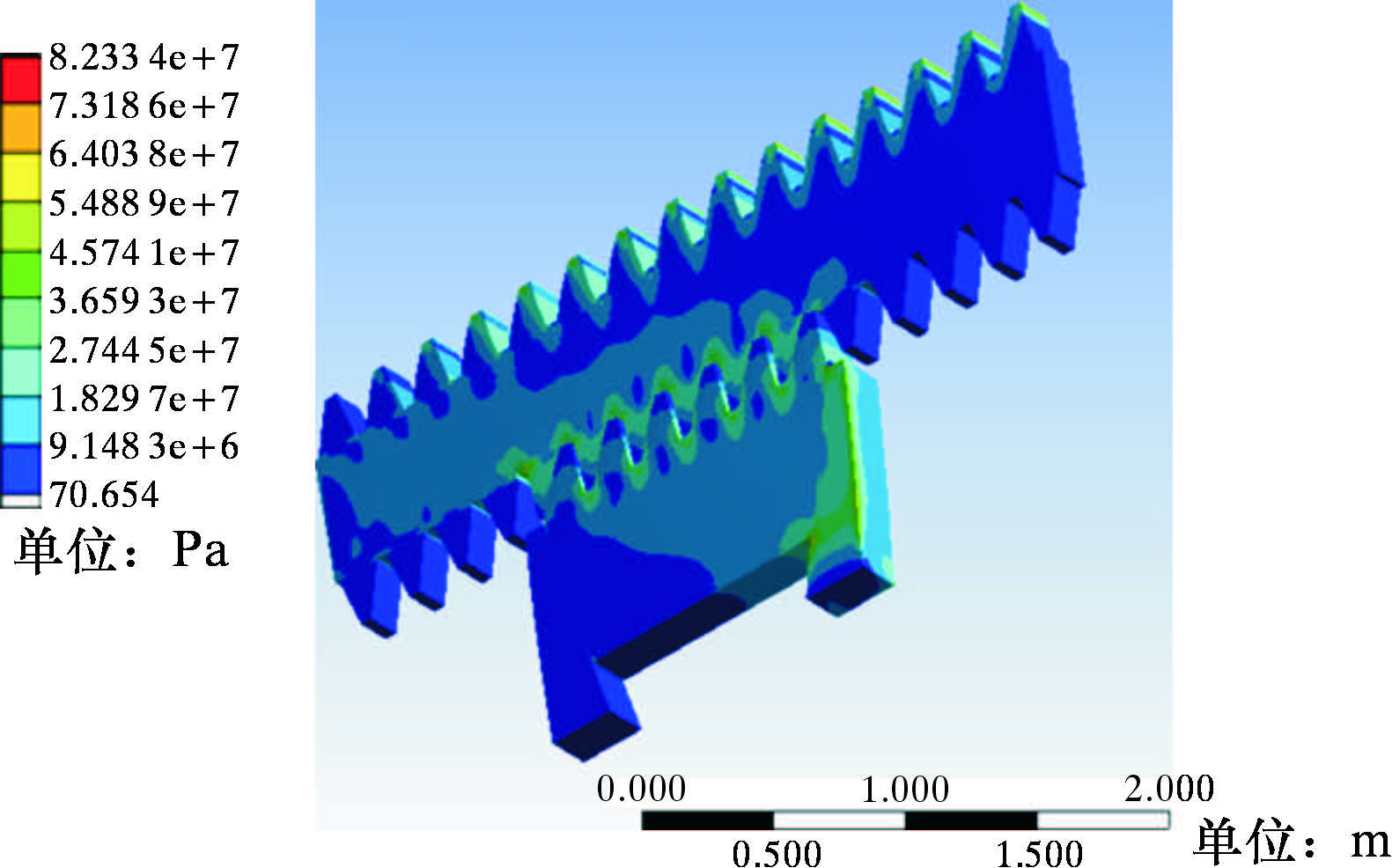
齿形楔块锁紧系统的接触应力如图 5所示,最大接触应力为83 MPa,远小于材料许用应力极限,安全可靠。最大应力发生在齿面相接触的位置,齿根应力较小,随着与接触中心距离的增加,接触应力逐渐减小,齿根以内的部分应力较小,云图与理论和实际相符合。表明计算施加载荷和约束能够模拟出实际情况。
|
| 图 5 锁紧系统应力云图 Fig. 5 Stress distribution of the locking system |
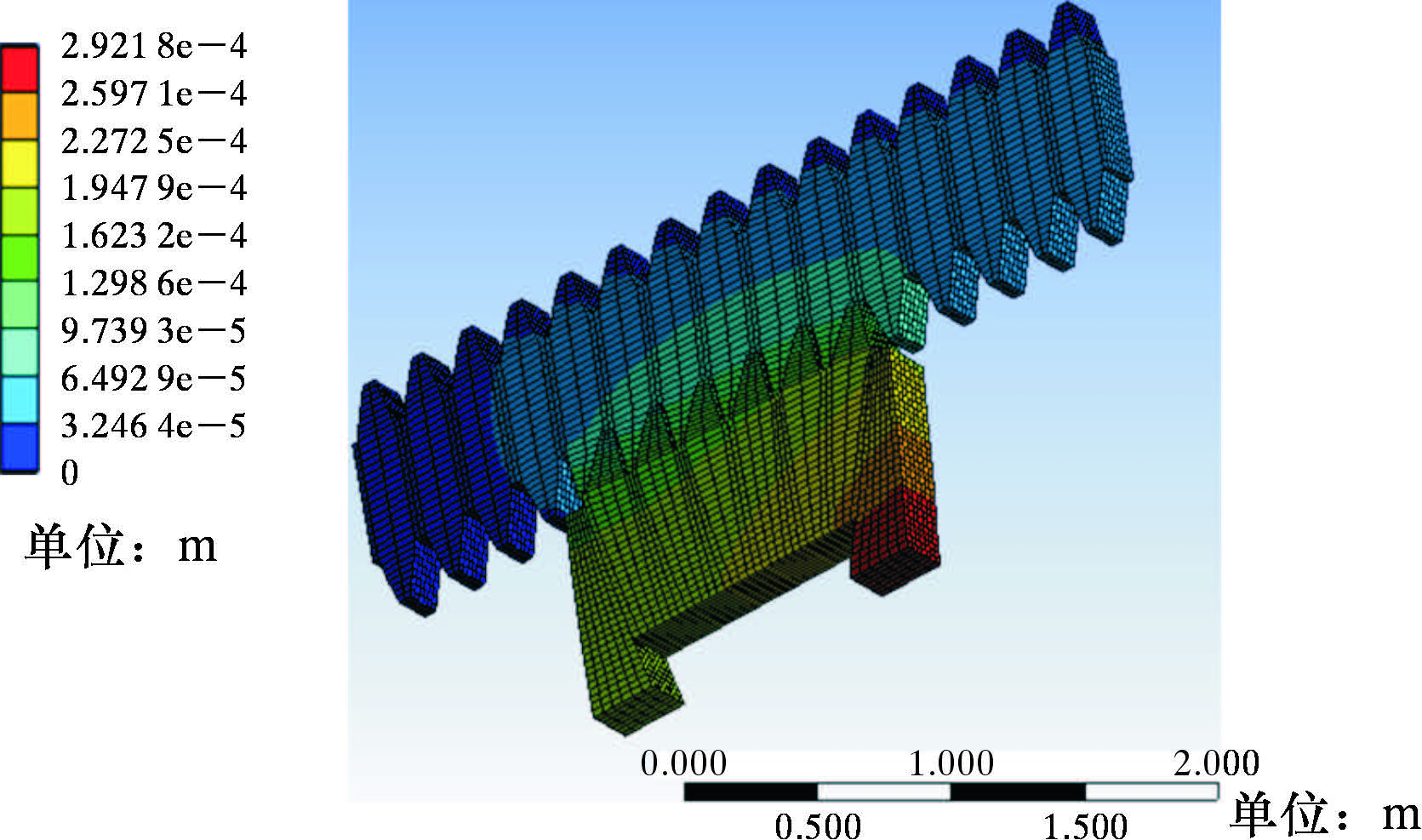
齿形楔块锁紧系统的接触应变如图 6所示,锁紧系统整体变形微小,齿条上部的变形量相对较大,约0.3 mm,这也与变形协调方程所求的指数方程趋势基本一致,完全满足对平台形变的设计要求。
|
| 图 6 单侧锁紧系统变形云图 Fig. 6 Deformation distribution of the unilateral locking system |
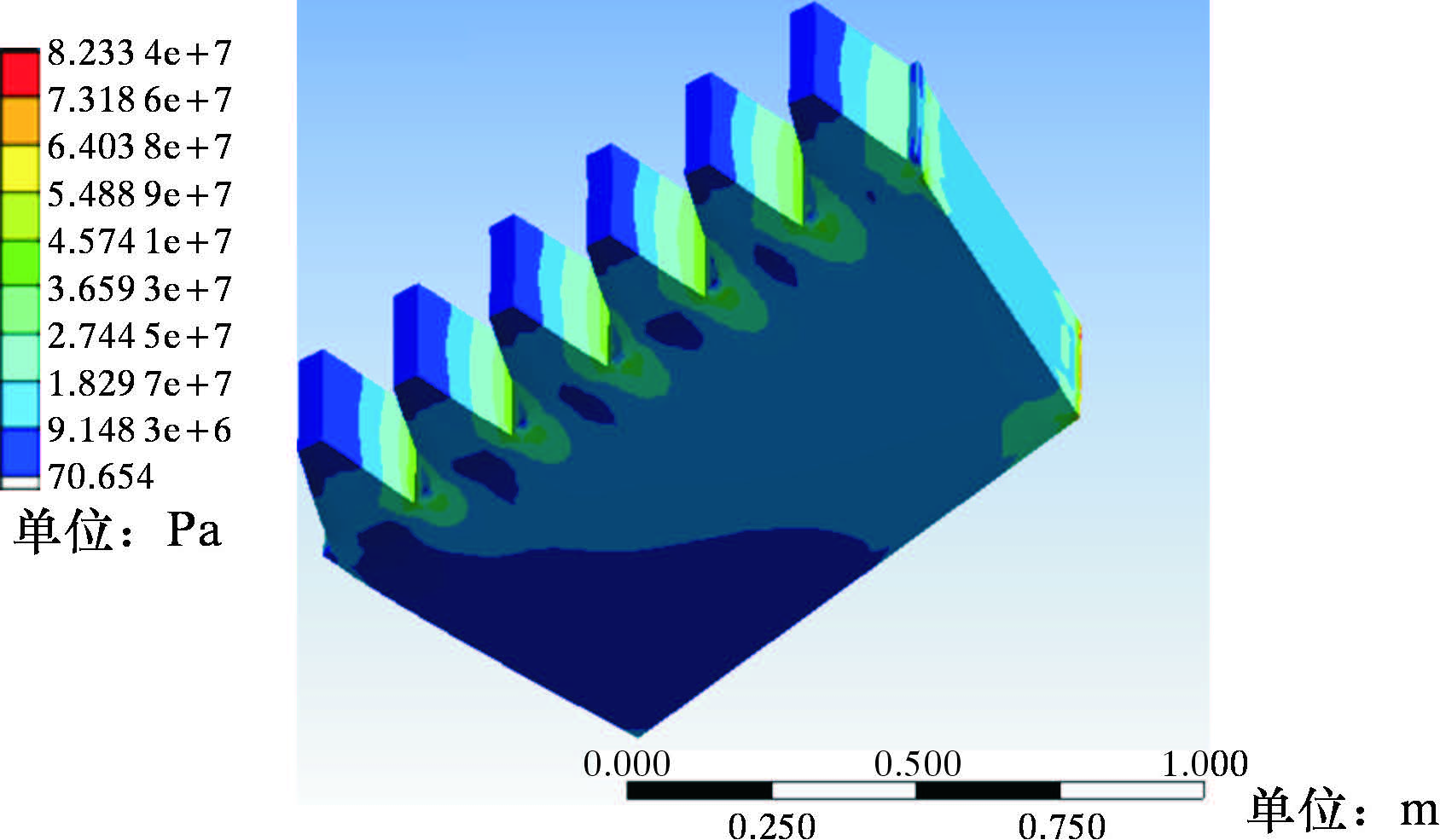
齿条锁紧块的应力如图 7所示,由于对蜗轮蜗杆竖直方向载荷施加,齿形楔块上部应力较大,最高可达82 MPa。齿形楔块结构紧凑,接触约束较多,对材料应力变形限制较大,因此完全能够满足平台锁紧时的载荷要求。
|
| 图 7 齿形楔块应力云图 Fig. 7 Stress distribution of the tooth-shape wedge block |
在齿条研究方面,尼曼等人使用有限元法研究认为压力角28°左右时最好。K.V.Senthil[12]用有限元法分析了渐开线圆柱齿轮齿根强度的齿轮参数,A.L.Kaplevich等[13]使用有限元法对齿根弯曲强度进行了优化分析。
唐文献等[14]研究认为,影响渐开线圆柱齿轮齿廓形状的齿数、变位系数、压力角、齿顶高系数、齿顶系数、齿根圆角半径系数及模数等参数在超大齿形楔块啮合计算过程中会对齿面接触强度和齿根弯曲强度产生影响。为此,确定采用模数95,压力角30°,齿条宽200 mm。利用Pro/E建立三维模型,并做简化处理,导入ADAMS中将不同的构件连接起来组成一个机械系统[15],在仿真环境中添加各种约束模拟机构的相对运动,如图 8所示。

|
| 图 8 齿形楔块锁紧系统模拟仿真图 Fig. 8 Simulation of the tooth-shape wedge block locking system |
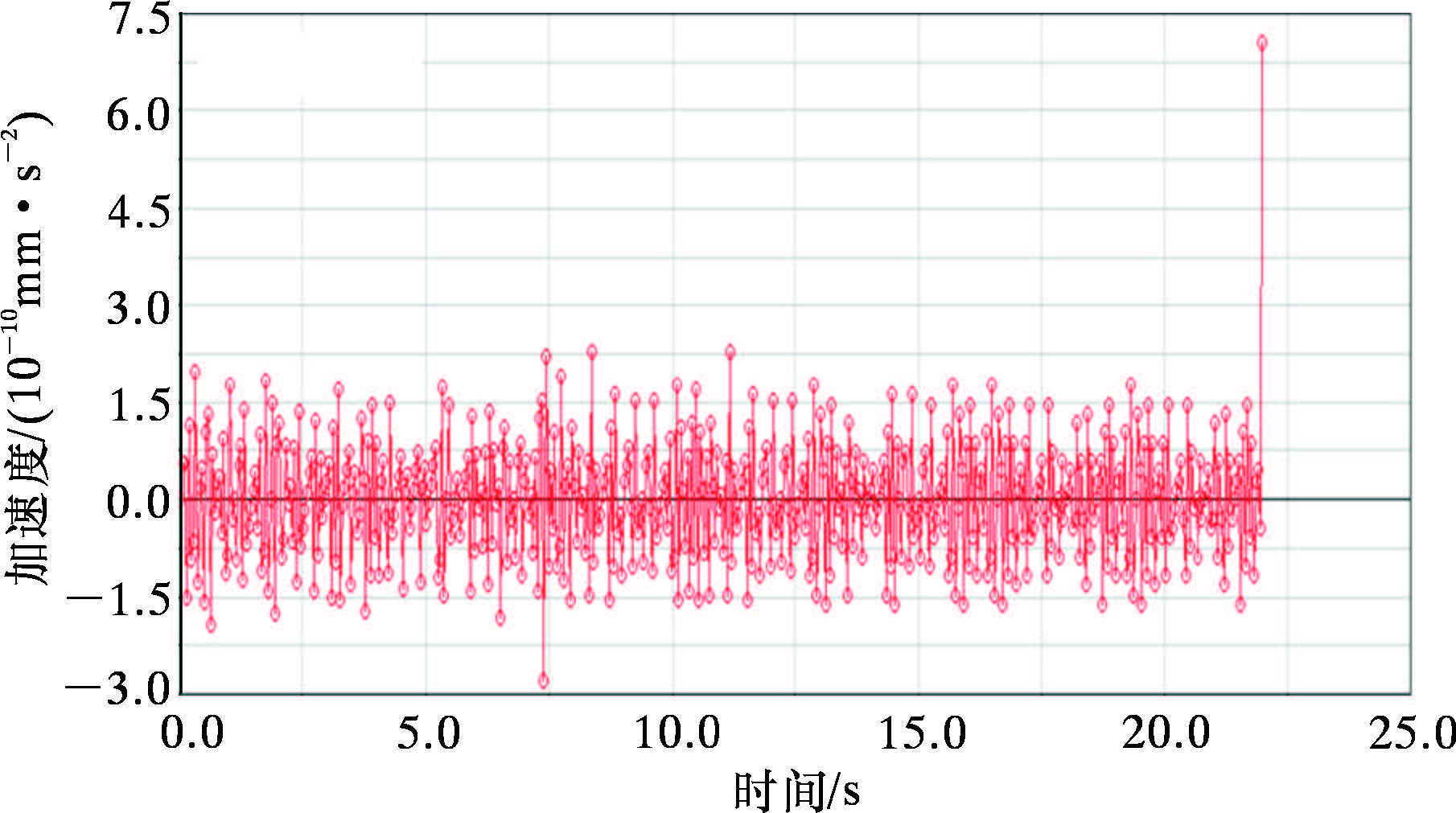
液压缸推动齿形楔块向桩腿齿条方向运动,液压缸对活塞的动力转化成水平施加恒力载荷,在ADAMS三维模型中[16]做简化处理,将螺杆传动总成简化处理成滑移驱动约束,建立滑移铰,并添加移动副,定义材料属性和接触参数。根据液压缸的行程以及速度,确定仿真时间为22 s。仿真结束后,得到运动的实时加速度与时间关系如图 9所示。
|
| 图 9 锁紧系统齿条块加速度与时间关系图 Fig. 9 The acceleration of the locking system rack versus the time |
齿条块夹紧过程中,由于自身重力较大以及相互摩擦接触作用影响,所以在运动过程中加速度不恒定。由图 9可知,其加速度在0附近小幅振荡,加速度峰值达2.0×10-10 mm/s2,对于齿条块的平稳运动基本无影响,保证齿条块与桩腿齿条顺利啮合,不会发生错齿现象。当齿块与齿条接触时,质量约1 t的齿条块会造成冲击载荷,加速度虽然向上突增达到7.2×10-10 mm/s2,但由于加速度过小,导致惯性力过小,不会对齿条造成明显冲击破坏。
5 结 论(1)针对高载荷平台对于锁紧功能的苛刻需求,设计出齿形楔块式锁紧系统,可通过楔形块和螺杆进行载荷转移、锁紧和解锁操作。针对平台锁紧安全稳定的要求,利用蜗杆传动具有的自锁性,设计出蜗轮蜗杆锁紧系统。齿形楔块利用楔形块自锁的特点,同时从垂直和水平方向约束锁紧齿条。
(2)采用ANSYS计算出静载荷下齿面的接触应力和应变,锁紧系统整体变形微小,齿条上部的变形量相对较大,这与变形协调方程所求的指数方程趋势基本一致,计算结果与实际情况相符。齿根部分应力较小,基本与实际情况相符合,表明计算施加载荷和约束能够模拟出实际情况。
(3)利用Pro/E建立锁紧系统三维模型,在ADAMS仿真环境中模拟系统的锁紧运动情况,结果表明,在运动过程中,齿条块加速度虽不恒定,在0附近小幅震荡,但对于齿条块的平稳运动基本无影响。接触时,齿条块加速度突然变大,但对于齿条的冲击载荷相对较小,可以保证齿条块与桩腿齿条顺利啮合。
| [1] | 蒙占彬,曹宇光,张士华.自升式平台齿轮齿条升降系统结构设计[J].机械设计与制造,2013(11):33-35. |
| [2] | 李佩泉,毕长飞.基于ADMAS的行星齿轮传动系统运动学仿真分析[J].机械,2009,36(10):19-21. |
| [3] | Tan X M,Li J,Lu C.Numberical analysis of jacking operation for a self-elevated jack-up unit[J].Computers & Structures,2003,19(2/3):152-159. |
| [4] | 周欣.自升式海洋钻井平台异形蜗轮蜗杆锁紧机构设计研究[J].河南科技,2014(6):103-104. |
| [5] | 尼曼·G,温特尔·H.机械零件[M].余梦生,译.北京:机械工业出版社,1989. |
| [6] | 张争艳.自升式海洋钻井平台齿轮齿条爬升与锁紧系统设计与研究[D].武汉:武汉理工大学,2011. |
| [7] | 李金澎.大模数直齿轮轮齿弯曲强度与齿面接触研究[D].大连:大连理工大学,2007. |
| [8] | 徐芝纶.弹性力学简明教程[M].北京:高等教育出版社,2002. |
| [9] | 薛军,孙宝玉,幸宏伟,等.基于有限元法的齿轮齿条动态应力分析[J].长春工业大学学报:自然科学版,2008(6):275-278. |
| [10] | 张兴权,何广德,郑茹,等.齿轮齿条的接触应力研究[J].机械传动,2011,35(7):30-32. |
| [11] | 曹宇光,张卿,张士华.自升式平台齿轮齿条强度有限元分析[J].中国石油大学学报:自然科学版,2010,34(6):120-124. |
| [12] | Senthil K V,Muni D V,Muthuveerappan G.Optimi- zation of asymmetric spur gear drives to improve the bending load capacity[J].Mechanism and Machine Theory,2008(43):829-858. |
| [13] | Kapelevich A L,Shektman Y V.Direct gear design bending stress minimization[J].Gear Technology,2003,25(5):44-47. |
| [14] | 唐文献,马宝,吴琼.超大模数齿轮齿条承载能力影响因素研究[J].机械科学与技术,2013(2):294-299. |
| [15] | 徐长航,苑思敏,陈国明,等.自升式平台齿轮齿条升降装置动力学行为分析[J].石油机械,2013,41(7):49-53. |
| [16] | 洪嘉振,刘绵阳.机械系统计算动力学与建模[M].北京:高等教育出版社,2011. |



