0 引 言
齿轮齿条钻机利用齿轮与齿条起升系统带动顶驱上、下运动,能够为钻柱提供上拉力或下压力,非常适合于定向井、丛式井和水平井的钻井工作[1]。齿轮齿条钻机起升系统工作时,不但会因为外部激励作用而产生动态响应,而且会因为啮合齿对数的改变、轮齿的弹性变形及轮齿误差等内部激励因素而导致啮合刚度发生变化,从而产生轮齿动态啮合力,而这种由于啮合综合刚度的时变性引起的动态激励是齿轮传动中最主要的动态激励形式之一[2]。因此,研究齿轮齿条内部激励下的动态响应,是确定钻机起升系统动力学性能的重要前提。
目前,国内外学者对齿轮内部激励的动态响应分析主要集中在时变啮合刚度的计算,并已取得大量研究成果[3, 4, 5]。T.Kiekbusch等[6]最早提出了直齿轮时变啮合刚度的经验公式;J.J.Zhang等[7]利用有限元方式计算了斜齿轮的时变啮合刚度;S.Jia等[8]运用三维有限元模型计算出齿轮有剥落和裂纹时的单级齿轮外啮合刚度;黄胜军等[9]运用能量法针对裂纹状态下行星齿轮的啮合刚度进行建模分析;邵毅敏等[10]提出了一种轮齿表明剥落缺陷的时变刚度算法。虽然关于齿轮时变啮合刚度的研究已较为深入,取得了一些成熟的计算方法,但是关于齿轮齿条内部激励下动态响应分析的解析或数值方法研究鲜有报道。
笔者通过建立齿轮齿条啮合动力学模型,分析了齿轮时变啮合刚度对系统动态响应的影响规律,并利用Solidwork与ADAMS联合建模方法,进一步分析了起升系统在不同工况下齿轮齿条之间的接触力以及齿轮转速随时间的变化规律,为齿轮齿条钻机起升系统的机构优化设计提供参考。
1 齿轮齿条啮合的动力学模型[11] 1.1 齿轮齿条啮合的动力学模型齿轮齿条啮合的动力学模型如图 1所示。系统忽略传动轴及支承系统的变形,只考虑齿轮副的变形,其中齿轮的基圆半径为r,综合啮合刚度为kv,齿廓误差为e,啮合阻尼系数为cv,齿轮上的驱动力矩为T,齿条上的阻力为G。齿轮的转角和转动惯量分别为θ和J,齿条的位移和质量分别为s和m,齿轮旋转方向取顺时针为正。
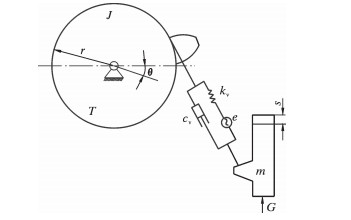
|
| 图 1 齿轮齿条啮合的动力学模型 Fig.1 Dynamics model of gear rack meshing |
设重合度小于2,啮合齿对i(i=1,2,3,4即最多为4对轮齿啮合)在啮合线上的综合变形可写为:
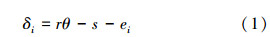
式中,ei为啮合齿对i的齿廓误差。
则考虑啮合阻尼的齿轮齿条动态法向啮合力可表示为:
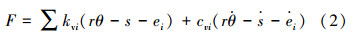
式中,kvi为啮合齿对i的啮合刚度;cvi为啮合齿对i的啮合阻尼系数。
齿轮齿条传动系统的力矩平衡方程为:
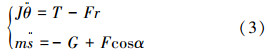
式中,α为啮合角,对标准齿轮α=20°,G为外部因素对钻柱的作用力,如钻井液的浮力等。
将式(2)带入式(3)得:
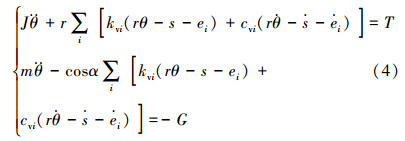
式(4)即为齿轮齿条啮合的动力学方程,其响应结果主要受时变综合刚度的影响,从而形成对整个起升系统的动力学影响。
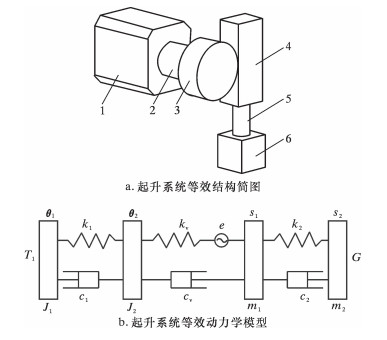
2 齿轮齿条起升系统的动力学模型根据起升系统的结构及其工作特点,假设在理想的工作情况下,每个齿轮的加工精度、安装误差、工况及载荷等因素都相同,则可将齿轮齿条起升系统看成为一个齿轮与齿条啮合的等效模型,如图 2a所示,并且齿轮只有旋转运动,而齿条是移动的,同时将负载施加在齿条上,则相应的动力学模型如图 2b所示。
|
| 图 2 起升系统动力学模型 Fig.2 Dynamics model of hoisting system 1-原动机;2-传动轴;3-齿轮;4- 齿条;5-顶驱主轴;6-钻柱负载。 |
其中T1、J1和θ1分别为原动机的驱动扭矩、转动惯量和转角;k1和c1分别是其扭转刚度系数和扭转阻尼系数;J2和θ2是齿轮的转动惯量和转角;s1和m1是齿条的垂直位移和质量;k2和c2分别是负载连接轴的伸缩刚度系数和伸缩阻尼系数;s2和m2是负载的垂直位移和质量。
与齿轮齿条啮合动力学方程的建立方法类似,根据式(4)可建立起升系统动力学方程为:
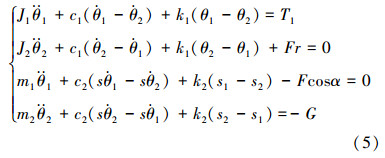
齿轮齿条钻机采用齿轮齿条啮合的传动方式带动顶驱升降运动来实现钻修作业。该钻机的 起升系统相当于有限齿数的小齿轮和无限齿数的大齿轮相互啮合,是一种将转动精确转换为直线运动的传动机构。
ADAMS 提供的齿轮副是一种专门用于模拟齿轮对啮合运动关系的约束,但它具有的三维建模能力相对薄弱,可以通过与其他三维建模软件,如SolidWorks、UG和Pro/E等进行数据交换。就是采用Solidworks建立齿轮齿条钻机起升系统的三维实体模型,以便导入ADAMS对起升系统进行后续的动力学仿真,齿轮齿条的几何参数如表 1所示。其中,齿轮齿数为14,齿条长度为2 m。
| 几何参数 | 齿轮 | 齿条 |
| 模数/mm | 25 | 25 |
| 压力角/(°) | 20 | 20 |
| 齿宽/mm | 175 | 175 |
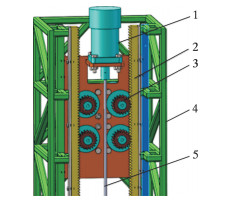
图 3所示为起升系统三维装配模型。这里主要考虑起升系统齿轮齿条啮合情况的工作特性,不考虑井架的变形等其他因素的影响,因此将井架以及其他附属部件忽略或简化,只保留了起升系统及齿条。
|
| 图 3 起升系统三维装配模型 Fig.3 3D assembly model of the hoisting system 1-顶驱;2-齿条;3-齿轮;4-井架;5-钻柱。 图3起升系统三维装配模型 |
将Solidworks装配好的三维实体模型保存成x_t格式,将输出的文件放到非中文路径下。运行ADAMS软件,打开view,选import a file,在路径里选择相应文件夹,点击ok,接下来在弹出的对话框里在file type处选择Parasolid中的ASCII项,在file to read里双击,选择上述保存的x_t格式三维实体模型,在model name里点击右键,依次选择MODEL和create,点击ok。模型如图 4所示。

|
| 图 4 基于ADAMS的齿轮齿条啮合模型 Fig.4 ADAMS-based gear and rack engagement model |
为了模拟起升系统的工作情况,需要根据起升系统的实际工况分析其部件之间的运动关系,并对模型添加边界条件,具体设置如下。
(1)创建运动副。齿条与井架之间添加固定副,滑动装置与齿条之间添加移动副,齿轮与滑动装置输出轴之间添加转动副。由于齿轮与齿条之间的齿轮副只能保证齿轮与齿条间的运动关系,而无法模拟彼此之间的接触力,所以不需要添加齿轮副,而是要定义接触。
(2)添加驱动。起升系统是由4个齿轮驱动,因此对4个齿轮的转动副添加旋转驱动。这里需要注意的是起升系统有4个齿轮,在起升过程中左侧2个齿轮逆时针旋转,而右侧2个齿轮则是顺时针旋转,在下降过程中转向则相反,因此在起升和下降的仿真过程中要注意旋转驱动的方向。
(3)定义接触。在ADAMS中有2种方法可以模拟计算出接触力:补偿法(Restitution)和冲击函数法(Impact)。采用冲击函数法来模拟齿轮与齿条之间的接触力,其表达式为[12]:
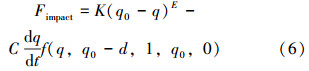
式中,q为2个物体接触未变形时的距离,q0为2个物体接触变形后的距离,K为接触刚度系数,E为碰撞指数,C为阻尼系数,d为阻尼达到最大时的距离,即切入深度,t为时间。
经计算设置K=1.87×1011 N/m3/2,阻尼系数通常设为刚度系数的0.1%~1.0%,其余参数可采用ADAMS推荐值或经验值。
(4)施加载荷。由于钻柱在井中的粘滞阻尼受钻井液、井壁以及钻柱的运动情况等多种因素影响,所以确定其作用力过程极为复杂。将其等效为具有质量-弹簧-阻尼的等效力,设钻杆的等效质量为34 230 kg,等效刚度为7.43×105 N/m,等效阻尼为50 kN·m/s。
(5)仿真时间与步长设置。由于齿轮齿条的啮合过程具有周期性,所以无需将仿真时间设置的过长,同时也是为了缩短计算时间,设置仿真时间为2 s。为了提高求解的稳定性,根据实际试算时间和精度进行综合考虑,设置步数为5 000。
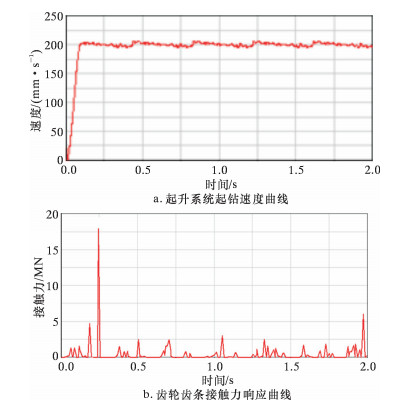
4.3 计算结果与分析 4.3.1 起钻过程当起升系统以最大负载起钻工作时,设定起升系统自身重力为50 kN,钻柱重力为350 kN,起钻速度为0.2 m/s。起升系统起钻时的仿真分析结果如图 5所示。
|
| 图 5 起升系统起钻时的仿真结果 Fig.5 Simulation results of the hoisting system during tripping out |
图 5a为起升系统起钻时的速度曲线。起升系统起钻速度开始随时间递增或递减发生变化,然后趋于稳定,这主要是由齿轮与齿条啮合过程中的内部激励产生的。图 5b为齿轮齿条啮合的接触力曲线,接触力随时间有一个近似的周期变化,这是因为轮齿啮合刚度出现周期性变化,接触力也是按照啮合刚度的变化而产生周期性变化。接触力局部存在较大的尖峰,这是由于小齿轮齿条之间的啮合冲击所致。对比图 5a和图 5b可以看出,接触力尖峰与起升系统速度曲线尖峰相对应。
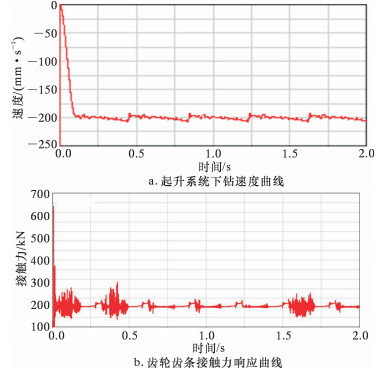
4.3.2 下钻过程同样以最大负载下钻工作时,设定下钻速度为0.2 m/s,其仿真分析结果如图 6所示。
|
| 图 6 起升系统下钻时的仿真结果 Fig.6 Simulation results of the hoisting system during tripping in |
由图 6a可以看出,起升系统下钻时,其下钻速度曲线也随时间变化,然后基本恒定。图 6b中的齿轮齿条接触力响应曲线仍然呈现周期性冲击规律,其振动幅值也比起钻过程相应提高,同时与起升系统速度曲线的冲击时刻具有一致性。
5 结 论(1)由于内部激励作用,齿轮齿条钻机起升系统速度曲线开始随时间发生变化,后期会趋于恒定。
(2)齿轮齿条钻机起升系统的啮合接触力曲线与起升系统速度曲线随时间存在冲击峰值的同步性。
(3)工况相同条件下,与起钻过程相比,起升系统下钻过程的振动幅度变化较大,起升系统速度曲线幅值与齿轮齿条啮合接触力曲线振动幅值同时增加。
| [1] | 常玉连,李军,任福深,等.具有主动加压钻进功能钻机的技术发展[J].石油机械,2013,41(1):1-5. |
| [2] | 唐进元,王志伟,雷敦财.载荷与齿轮啮合刚度、重合度的关系研究[J].机械传动,2014,38(6):1-4. |
| [3] | 徐长航,苑思敏,陈国明,等.自升式平台齿轮齿条升降装置动力学行为分析[J].石油机械,2013,41(7):49-53. |
| [4] | Zhou X J,Shao Y M,Lei Y G,et al.Time-varing meshing stiffness calculation and vibration analysis for a 16DOF dynamic model with linear crack growth in a pinion[J].Journal of Vibration and Acoustics,2012,134(1):1-11. |
| [5] | Chen Z G,Shao Y M.Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack[J].Mechanism and Machine Theory,2013,62:63-74. |
| [6] | Kiekbusch T,Howard L.A common formula for the co- mbined torsional mesh stiffness of spur gears[C]//5th Australasian Congress on Applied Mechanics,2007:172-179. |
| [7] | Zhang J J,Esat I I,Shi Y H.Load analysis with var-ying mesh stiffness[J].Computers and structures,1999,70(3):273-280. |
| [8] | Jia S,Howard I.Comparison of localized spalling and crack damage from dynamic moding dynamic modeling of spur gear vibrations[J].Mechanical System and Signal Processing,2006,20(2):332-349. |
| [9] | 黄胜军,张建宇,胥永刚.单齿裂纹状态下行星齿轮啮合刚度的计算方法[J].振动与冲击,2014,33(增刊1):120-122. |
| [10] | 邵毅敏,王新龙,刘静,等.基于边缘接触时变刚度的齿轮表面剥落动力学模型与响应特征[J].振动与冲击,2014,33(15):8-14. |
| [11] | 李军.齿轮齿条煤层气钻机起升系统设计与研究[D].大庆:东北石油大学,2013. |
| [12] | 李增刚.ADAMS入门详解与实例[M].北京:国防工业出版社,2006. |




