2. 长江大学机械工程学院;
3. 中国石油集团钻井工程技术研究院康布尔公司
2. School of Mechanical Engineering, Yangtze University;
3. Kembl Petroleum Technology Co., Ltd., CNPC Drilling Research Institute
0 引 言
当前,连续管套管内开窗侧钻正逐渐成为国内外油气田后期开发的一种经济、安全、有效的手段[1]。但是,连续管开窗受井下马达输出扭矩限制,一旦施工钻压控制不当,极易造成动力马达失速甚至破坏[2],严重影响开窗轨迹、开窗速度和窗口质量。在国内,连续管开窗侧钻还处于起步探索阶段,现场多采用厂商推荐以及工程经验钻压,对作业钻压缺少有效的预判。
针对以上问题,笔者以目前国外连续管套管内开窗普遍采用的造斜器开窗为研究对象,基于纵横弯曲法的相关理论,考虑井身结构和钻具组合对钻压的影响,对一维井身下开窗过程中的合理作业钻压区间进行了预测研究,研究结果有助于提高开窗窗口质量,减少作业事故的发生。
1 连续管套管内开窗工具目前,国外Baker Oil Tools[2]、Schlumberger[3]和BJ[4]公司多推荐或采用造斜器配合具有低攻击性的先导铣鞋(Leading Mill,以下简称LM)和扩眼铣鞋(Reamer Mill,以下简称RM)构成的组合工具实施套管开窗作业,组合式开窗铣鞋既能均匀承担磨铣量,又对整个钻柱起到扶正作用,有利于延长铣鞋寿命和加长窗口,实现一趟下井完成开窗。笔者将以2铣鞋的组合铣鞋工具为对象,开展钻压预测研究。
2 开窗钻压预测力学模型“纵横弯曲法”是白家祉于1982年提出,并成功应用于求解多扶正器钻具组合的受力与变形分析。它将一个多扶正器钻具组合看成是一个受有纵横弯曲的多支点连续梁柱,在扶正器处将其分成几个简支梁柱,然后可建立一组“三弯矩方程”组,以解出各扶正器处的内弯矩、钻头上受到的侧向力以及加于各扶正器上的约束反力等。经过国内外试验和现场验证,该方法具有模型合理、物理意义清晰、解法简洁以及计算精确等特点,随着计算机的发展和运用,其相应的计算变得更简单[5]。
笔者研究的连续管套管内开窗具有以下特点:
(1)对于开窗组合铣鞋工具(LM+RM),可以将其看作是单钟摆钻具组合,RM则是具有切削作用的稳定器;
(2)开窗位置位于长斜/直井段内;
(3)
仅选取连续管与井壁最下端的一个接触点到LM之间的钻柱进行力学分析研究;
(4)开窗井底钻具组合具有一定刚度,在轴向力作用套管的约束下发生小弹性变形;
(5)铣鞋开窗动力由井下马达提供,不涉及钻柱的整体转动。
对比垂直钻井系统井下钻具组合的纵横弯曲连续梁的力学模型所做的八项基本假设[5],连续管开窗工具受力变形特点基本满足纵横弯曲法模型建立的要求。笔者将基于纵横弯曲连续梁的力学模型,建立一维井身[5]下的开窗钻压预测力学模型。
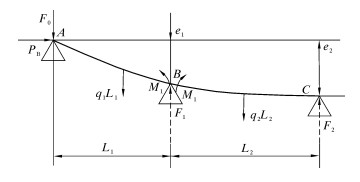
2.1 铣鞋与井壁的接触力开窗组合铣鞋工具(LM+RM)支反力的计算如图 1所示。PB为钻压,N;F0为LM的侧向力,N;F1为RM的支反力,N;F2为钻杆与井壁的接触力,N;L1为LM与RM之间的距离,m;L2为上切点长度,m;井斜角为α,rad;q1、q2为管柱自重下的均布载荷,N/m;M1为RM处的弯矩,N·m,根据三弯矩方程组求得;e1为LM与RM偏心值,e2为LM与钻柱偏心值,mm。
|
| 图 1 开窗组合铣鞋工具支反力的计算 Fig.1 Calculation for reaction forces of the reamers of window |
假定RM与下井壁接触,井壁对RM产生支反力。若忽略第1跨L1钻铤自重纵向分量的微小影响,对支点B求矩,由∑MB=0得A点的侧向力:
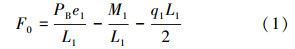
F0的性质与符号的关系是:若F0>0,则为造斜力;若F0<0,则为降斜力。
将AB和BC 2根梁看成一体(如图 1所示),对C点求矩,由∑MC=0得RM的支反力:
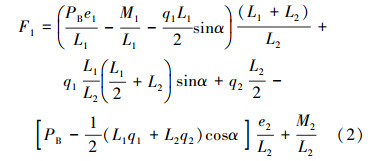
F1的性质与符号的关系是:若F1>0,则RM与下井壁接触;若F1<0,则RM与上井壁接触。
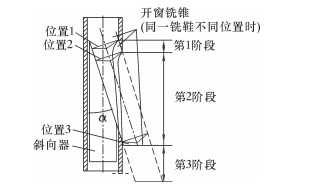
2.2 开窗扭矩为便于分析计算开窗过程中铣鞋切削所需扭矩,笔者将开窗过程分为3个阶段(见图 2)。
|
| 图 2 开窗过程中的3个阶段 Fig.2 Three stages of window milling |
第1阶段:从LM接触套管内壁高边到铣鞋底部圆周刚出套管外壁;
第2阶段:从LM底部圆周刚出套管外壁到铣鞋底部圆周刚好完全出套管外壁;
第3阶段:LM底部圆周刚好完全出套管外壁,并在地层中钻进。
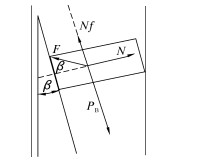
在第1阶段铣鞋只切削金属套管,并与造斜器导斜面摩擦,受力如图 3所示。各力之间的关系为:
|
| 图 3 在第1阶段内LM沿导斜面滑动时的受力 Fig.3 The force acting on the mill when LM moves along the inclined guiding plane in the first stage |
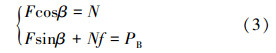
式中,F为套管内壁与LM的接触力,N;N为造斜器导斜面的接触力,N;β为导斜面倾角,rad。
此时钻具组合上的总扭矩为:
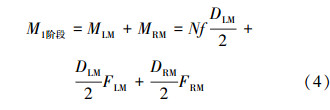
式中,M1阶段为作用在LM和RM上的总扭矩,N·m;MLM为LM上的扭矩,N·m;MRM为RM上的扭矩,N·m;f为LM与导斜面的摩擦因数;FLM为LM上的切削力,N;FRM为RM上的切削力,N;DLM和DRM分别为LM和RM的直径,m。
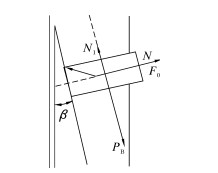
在第2阶段铣鞋既切削套管,又破碎水泥石,受力分析如图 4所示。各作用力之间的关系为:
|
| 图 4 在第2阶段内LM沿导斜面滑动时的受力 Fig.4 The force acting on the mill when LM moves along the inclined guiding plane in the second stage |

式中:N1为地层给LM的轴向作用力,N。
需要说明的是,由图 4可以看出铣鞋底面圆受力不均匀,导致LM上存在一定的偏心,即存在一定的弯矩[6]。LM上弯矩的存在很有可能导致LM与导斜面产生接触力(图 4中的力N)。为了简化,这里不考虑偏心力的影响,且假定钻压全部作用在套管上。
此时钻具组合上的总扭矩为:
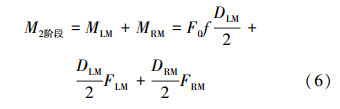
式中,M2阶段为作用在LM和RM上的总扭矩,N·m;MLM为LM上的扭矩,N·m;MRM为RM上的扭矩,N·m。
在第3阶段内,LM铣鞋只切削地层。对于LM除了底端面在钻压作用下破碎岩石外,其保径部分在大于某一侧向力值作用下也会切削岩石,否则仅考虑LM保径部分转动摩擦产生的扭矩。
此时钻具组合上的总扭矩为:
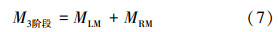
式中,M3阶段为作用在LM和RM上的总扭矩,N·m。
在以上3个阶段内,RM与套管或井壁的接触力大于某个数值时产生切削作用,否则仅考虑转动摩擦产生的扭矩。假定LM或RM与导斜面接触时,不论其侧向力大小,铣鞋都不切削导斜面,只与导斜面产生摩擦作用。
LM和RM钻进时,钻压和扭矩的关系可通过理论近似计算或试验方法对特定铣鞋进行测定,经过拟合得到一定关系曲线。
3 开窗钻压预测与窗口质量控制 3.1 连续管开窗补充假设(1)造斜器为刚性体,与井眼中心同心;
(2)铣鞋开窗过程中不发生磨损,不会产生径向尺寸减小;
(3)铣鞋轴向长度短,可把铣鞋看作一个具有一定半径的平面圆;
(4)LM侧向力与钻压比值较小时,其始终沿着造斜器的导斜面及其延长面移动;
(5)连续管开窗钻具组合的长度总是大于LM与上切点之间的距离;
(6)井下马达与钻杆或钻铤具有相同的截面,马达输出扭矩恒定。
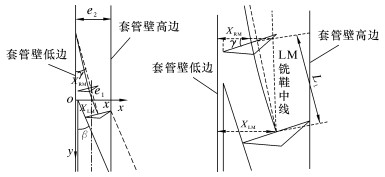
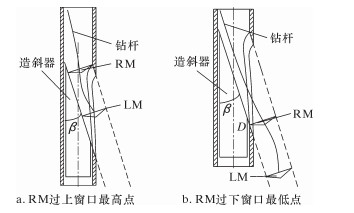
3.2 铣鞋的位置与接触判定规则 3.2.1 铣鞋位置(1)LM的新位置(矢量方法——θ规则)[7]。如图 5所示,在一维井身下,以套管内壁低边为y轴,以垂直于套管内壁方向为x轴建立直角坐标系。当在LM上施加钻压P时,由侧向力F0所产生的角度为:
|
| 图 5 LM和RM铣鞋位置 Fig.5 Positions of LM and RM |
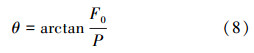
由于铣鞋在任何方向都具有切削作用,所以可以合理地假定铣鞋的钻进方向与加在铣鞋上的力的方向相同,如式(8)所示。
因此铣鞋新的增量在x方向上的移动为:

以上2个方程组成了θ规则,其中Δy是2铣鞋钻具组合沿y轴方向的一个单位增量。
根据式(8)和式(9)可知,只要作用在LM上的侧向力计算值为负,则LM沿着造斜器导斜面移动,反之按照上述的θ规则,LM离开造斜器表面,形成一个比导斜面角度更大的θ角[7],即LM开始切削套管并造斜。
LM铣鞋中心的位置可由下式表示:
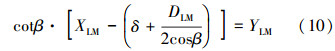
式中,XLM为LM铣鞋中心到套管内壁低边的距离,m;YLM为LM铣鞋中心到坐标系x轴的距离,m;δ为造斜器与套管内壁间隙,m。
(2)RM的位置。如图 5所示,考虑光钻铤井下钻具组合解,此时仅有LM切削。设LT是钻柱与井壁相切位置到LM的长度。由于XLM(LM中心与套管内壁间的距离)已知,切线梁所产生的平均角γ为:
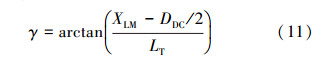
式中,DDC为钻铤直径,m。
当RM与井壁相切时,切线梁所产生的平均角γ为:
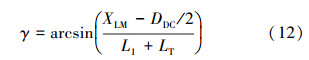
由于在LM和RM之间的长度L1已知,XRM为RM的中心和套管内壁低边之间的距离,则XRM为:
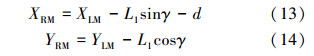
式中,d为RM位置处在光钻铤钻具上对应的挠度,m。
3.2.2 RM与井壁接触判定(1)LM沿导斜面移动量小于LM与RM之间的长度L1。 此过程中,RM仍位于套管内,RM与套管内壁无接触时有:
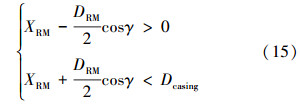
式中,Dcasing为套管内径,m;DRM为RM直径,m。
否则可判定RM与套管内壁接触。
(2)LM沿导斜面移动量大于LM与RM之间的长度L1,小于导斜面长度与L1之和。 此过程中,RM铣鞋此时位于造斜器和RM已钻井壁之间,则RM铣鞋与井壁和造斜器均无接触时有:
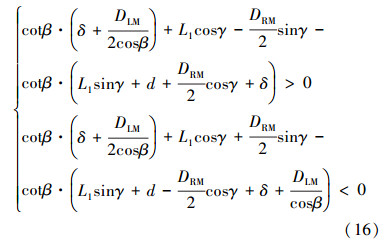
否则可分别判定RM与导斜面或已钻井壁接触。
(3)LM沿导斜面移动量大于导斜面长度与L1之和。 此过程中,RM完全处于地层中,其判断标准参考式(16)。
使用以上2式判据判定出RM与井壁接触后,再采用一个稳定器的白家祉模型计算RM侧向力的大小和正负,根据侧向力的正负判断RM与井壁高、低边接触情况。
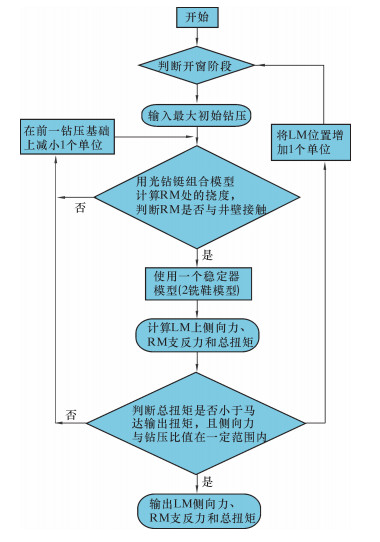
3.3 最大钻压预测迭代步骤最大的开窗钻压必须满足条件:在其作用下作用于LM和RM上的总扭矩不超过井下马达的输出扭矩,且能使LM沿着造斜器导斜面钻进(即LM上产生降斜力,或侧向力为0,或LM侧向力与钻压比值很小且在一定的范围内)。图 6为最大开窗钻压预测程序结构图。
|
| 图 6 开窗钻压预测迭代程序框图 Fig.6 Block diagram for WOB prediction during window milling |
在尽可能接近实际开窗作业工况下,为计算机迭代程序计算选取相应合适的基础数据如下。
连续管及套管尺寸:Φ73.0 mmCT,Φ139.7 mm×9.1 mm,N80套管。开窗地层砂岩。造斜器[8]直径108.0 mm,导斜面倾角1°55″。LM用Φ104.8 mm表镶金刚石速度铣鞋;RM用Φ104.8 mm的堆焊硬质合金扩眼铣鞋[9]。钻具组合尺寸:Φ88.9 mm×25.4 mm,弹性模量E=210 GPa,惯性矩I=296.26×10-8 m4。钻具浮重[10] 368 N/m,C5LZ95×7.0螺杆马达,最大扭矩2 235 N·m;借鉴机械加工上铣削及磨削经典理论和经验公式[11],以及金刚石钻头破岩特点[12]拟合得到一定曲线关系:F切1LM=0.56 F压1LM(F压1LM≥478 N)(切削套管),F切2LM=1.242 9 F压2LM(F压2LM≥4 192 N)(切削岩石),F切1RM=0.625 F压1RM(F压1RM≥193 N)(切削套管),F切1RM=0.71 F压1RM(F压1RM≥121 N)(切削岩石)。摩擦因数μ1=0.010(LM与造斜器导斜面),μ2=0.30(LM与砂岩),μ3=0.35(RM与套管和导斜面),μ4=0.40(RM与砂岩)。
4.2 合理开窗钻压预测及分析使用LM+RM组合铣鞋开窗时,理想作业状态下合理钻压范围既要满足最大钻压要求,又能使RM经过图 7所示的A、D 2点时具有加长和修磨窗口的作用,即RM在A点前后一段距离内与套管内壁高边接触(RM的支反力为负值),RM在D点前后一段距离内与造斜器导斜面和套管截面接触(RM的支反力为正值)。为便于编程和曲线分析,在3个开窗阶段基础上,以LM在导斜面上的行程(见图 8)和RM上的支反力F1为对象提取出2种工况(见表 1),以此求得相应工况下的极限钻压。当LM位于C点时,RM位于A点;当LM位于E点时,RM位于D点。
|
| 图 7 RM对窗口的加长和修磨作用 Fig.7 The lengthening and grinding effects of RM on the window |

|
| 图 8 LM沿导斜面的位移 Fig.8 Displacement of LM along the inclined guiding plane |
| 工况 | LM位于BC段 | LM位于CD段 | LM位于DE段 |
| 工况1 | F1<0 | F1<0 | F1<0 |
| 工况2 | F1<0 | F1≥0 | F1≥0 |
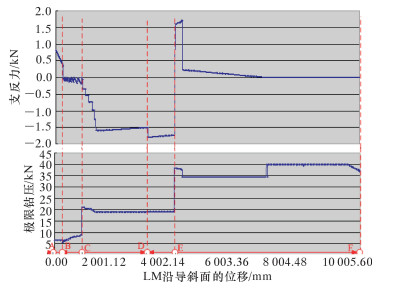
假定井斜角为2°,LM与RM之间的长度L1=1 000 mm时,根据表 1的工况,满足2种工况下的极限钻压和RM支反力如图 9和图 10所示。
|
| 图 9 工况1下的极限钻压和RM支反力 Fig.9 The extreme WOB and reaction force on RM under the first condition |
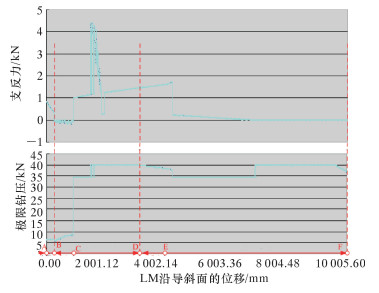
|
| 图 10 工况2下的极限钻压和RM支反力 Fig.10 The extreme WOB and reaction force on RM under the second condition |
由图 9和图 10可以看出,满足理想作业状态的钻压范围为:
(1)RM加长或修磨上窗口,即LM位于BC段时,施工钻压不超过工况1或工况2所示的最大钻压,LM位于CD段时,施工钻压不超过工况1所示的最大钻压。
(2)RM加长或修磨下窗口,即LM位于DE段靠近D点时,施工钻压不超过工况1所示的最大钻压,LM位于DE段靠近E点时,施工钻压取工况1和工况2所示的最大钻压之间的钻压值。
(3)RM位于其他位置的施工钻压可选取不超过工况1或工况2所示的最大钻压值。
2种工况下LM上的侧向力如图 11所示。
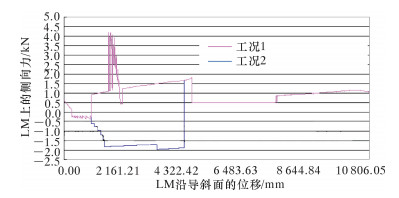
|
| 图 11 2种工况下LM上的侧向力 Fig.11 The lateral force acting on LM under two conditions |
由图 9、图 10和图 11可以看出:
(1)2种工况下LM上的侧向力和RM上的支反力符号相同,说明RM与套管内壁高边或已钻井壁高边接触时,LM上具有降斜力,RM与套管内壁低边或导斜面接触时,LM上具有增斜力,这些符合钻具的变形特点。
(2)当需要LM在D点位置上、下活动钻具修磨下窗口时,施工钻压不超过工况1所示的最大钻压。
此外,通过钻压曲线可以观察到以下现象:
(1)井下钻具组合在不同位置时允许的最大作业钻压是变化的,尤其是在开窗的第1阶段(初始开窗阶段),允许施加的最大钻压相对于其他位置小许多,这是因为初始阶段LM与套管内壁和造斜器的接触力很大,需要很大的切削扭矩,文献[13]也表明,连续管开窗初期极易发生马达失速现象,应当合理控制钻压。
(2)允许的最大钻压值在一些位置处有较大的突变,这是由于编程时将开窗过程分成了3个阶段,铣鞋切削的对象和RM接触条件不同,对应的计算模型存在差别。
(3)允许施加的钻压范围较大,一定程度上可反映出铣鞋的低攻击特性。
5 结论与认识(1)结合连续管套管内造斜器开窗特点,采用纵横弯曲法对一维井身下,开窗过程中合理施工钻压进行了预测研究,探索了一种连续管开窗作业钻压预测方法。
(2)连续管开窗钻压预测有利于保护钻具以及开出高质量窗口,对现场施工具有很好的指导意义。
(3)初始开窗阶段马达易发生失速,此时应施加较小钻压。
(4)研究中的假设条件以及计算示例中相关 基础数据选取与实际情况存在一定偏差,还需进一 步细化,计算得到的预测钻压与实际接近程度也需 现场验证。
| [1] | 赵卫红.连续软管钻井技术[J].钻采机械,2001,24(1):56-59. |
| [2] | Hupp J L,Johnson B,Wilson S,et al.Improvements in coiled-tubing window-milling operations cut costs and increase reliability,Prudhoe Bay,Alaska[R].SPE 68432,2001. |
| [3] | Leising L J,Hearn D D,Rike E A.Sidetracking technology for coiled-tubing drilling[R].SPE 30486,1996. |
| [4] | Blount C G,Gantt L L,Hearn D D,et al.Concentric string window:Development,testing and field experience[R].SPE63196,2000. |
| [5] | 白家祉,苏义脑.井斜控制理论与实践[J].北京:石油工业出版社,1990. |
| [6] | 李子丰,张欣,王鹏,等.套管开窗侧钻中钻头弯矩分析[J].石油钻采工艺,2010,32(5):13-16. |
| [7] | Patil H.Trajectory and window width predictions for a cased hole sidetrack using a whipstock[R].SPE 124443,2004. |
| [8] | 刘景伊,周全兴,刘贵芝.钻井工具使用手册[M].沈阳:科学出版社,1990. |
| [9] | 薛永康,吴大康,屈军勤.5 1/2"套管开窗侧钻技术在安塞油田的应用[J].长江大学学报:自然科学版,2008,5(3):162-164. |
| [10] | 陆剑中,孙家宁.金属切削原理与刀具[M].北京:机械工业出版社,1985. |
| [11] | 邓裕荣.表镶金刚石钻头钻压计算问题的探讨[J].地质与勘探,1980(12):70-73. |
| [12] | Faure A,van Elst H.Slim-hole and coiled-tubing window cutting systems[R].SPE27654,1994. |




