0 引 言
随着深井和高温高压井勘探开发活动的日趋频繁,窄密度安全窗口带来的钻井周期长、事故频繁和井下复杂等情况也变得越来越多[1]。控压钻井技术(MPD)的出现很好地解决了这个问题。控压钻井的本质是:使用闭合承压的钻井液循环系统,首先通过水力模拟计算来预测环空压力剖面,然后与测量数据进行对比,得到井口回压预控值,再通过控制压力系统自动调节节流阀开度来控制整个井眼的环空压力剖面,从而解决钻井中的复杂压力控制问题[2, 3, 4, 5]。
当前国内控压钻井的研究重点在控压钻井设备的研制开发上,精确的环空水力计算略显欠缺[6]。而精确的环空水力计算能提供更精确的井口回压预控值,以保证控压钻井的顺利进行。鉴于此,笔者通过选取工程上适用性较好的赫-巴流变模式,结合控压钻井原理及控压钻井工艺流程,将钻井过程划分为若干工况,以流型+过程+工况的组合模式得到井口回压计算方法,并对井口回压影响参数进行分析。
1 控压钻井原理控压钻井的核心就是对井底压力进行精确控制,将井底压力控制在安全密度窗口之内,保证钻进与停钻等一系列作业的安全进行。通常井底压力等于静液柱压力、环空压耗以及井口回压之和。忽略岩屑沉降和钻速变化对上返钻井液密度的影响,在一定深度下,静液柱压力可视为定值,环空压耗受排量、井身结构、钻井液性能、钻具组合和岩屑含量等多种综合因素影响,因此保持井底压力恒定的关键则是改变井口回压以补偿环空压力损耗的变化[7]。
控压钻井井底压力模型为:
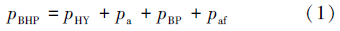
控压钻井一般使用较低密度的钻井液。井底恒压控压钻井有4种工况:钻进、起钻、下钻和接单根。
正常钻进时,系统环空压耗最大;停泵时,钻井液循环停止,环空压耗为0;起下钻作业时,环空中产生压力波动,此时应根据井下激动/抽汲压力的大小在井口实施回压来保持井底压力恒定。若遇到气侵状况,则需要降低泵的排量,将侵入流体低速循环出井,此时循环压降减小,需要适当增加井口回压。
2 井底恒压控压钻井井口回压计算将钻井过程划分为若干个工况,根据控压钻井的工艺原理,结合流型+过程+工况的组合模式来计算井口回压。
2.1 正常钻进过程井底压力模型循环钻进期间,井筒压力主要由钻井液静液柱压力和循环压耗组成,若地层压力过高,则还要对井口施加回压来平衡地层压力。正常钻进工况井底压力模型为:
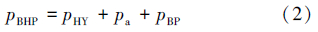
停泵过程由起下钻和接单根工况组成。起下钻会在井筒内产生压力波动,此时钻井液不循环,因此不存在环空循环压耗。井底压力的计算主要考虑静液柱压力、抽汲压力、波动压力及井口回压。起钻、下钻和接单根时的井底压力模型分别为:
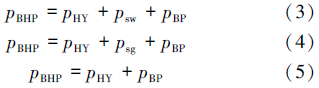
综上所述可得井口回压计算流程,见图 1。
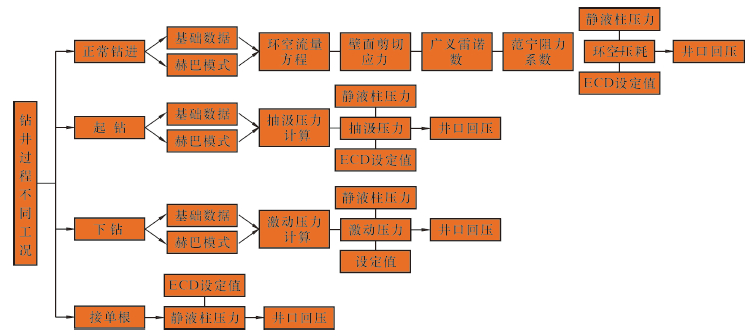
|
| 图 1 不同工况下井口回压计算流程图 Fig.1 The calculation flow chart of back pressure under different operation conditions |
钻井液流变性对环空水力模拟结果有着极其重要的影响。目前在石油工业中常用的流变模式有宾汉、幂律、卡森和赫-巴模式[8, 9, 10, 11]。赫-巴模式克服了幂律模式未考虑屈服值的缺点,而且能够较好地描述较高剪切速率下钻井液的流变性能,因此能够较准确地描述钻井液的流变性。其流变方程为:

基于圆管流量方程的压耗计算方法能准确分析钻柱内循环压耗。赫-巴流变模式能较准确地描述钻井液流变性,提高水力计算精度。将圆管流量方程应用于环空中,得到环空通用流量方程[12]:
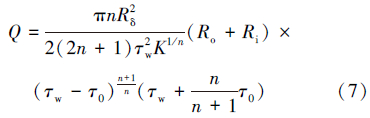
赫-巴流体环空结构流的广义雷诺数表达式为:
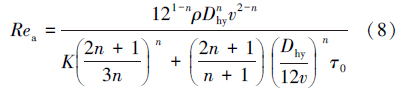
工程上常用广义雷诺数来判别赫-巴流体同心环空轴向流的状态,临界雷诺数近似取2 100,Rea<2 100时为层流,Rea≥2 100时为过渡流或紊流。
在层流条件下,环空压耗pa为:

紊流时采用非牛顿流体光滑管范宁阻力系数计算式[13]来计算Rea,即:
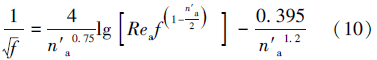
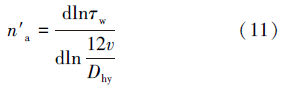
紊流时井眼环空循环压耗计算式为:

井下波动压力是破坏井眼压力系统平衡的主要原因之一,控制不好会造成井涌和井喷等安全事故。特别是在窄密度安全窗口井中,掌握波动压力的变化规律,计算波动压力的值,对于控压钻井的成功实施具有重要意义[14]。
实际起下钻工况下流速分布如图 2所示。基于稳态波动压力计算模型[15],对起下钻过程所产生的波动压力进行计算。
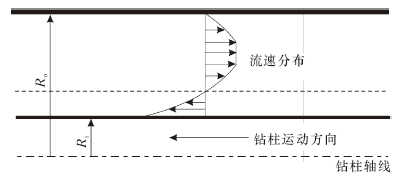
|
| 图 2 流速分布图 Fig.2 Mud velocity distribution |
参考Schuh 模型中提到的黏附系数来计算环空流速。下钻时环空上返流速为[16]:
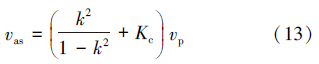
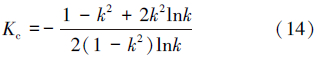
将式(14)带入式(13)得:
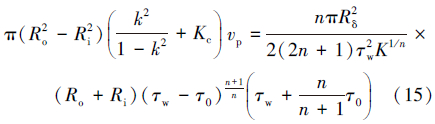
得到壁面剪切速率后,即可得波动压力梯度:

式(16)即为基于赫-巴流体的稳态波动压力计算方程,该方程同样适用于套管和起钻作业过程。起钻作业产生的是抽汲压力,与下钻时的压力大小相等,方向相反。
6 实例计算及分析 6.1 模型验证用实例井对井口回压计算模型进行验证。该井在2 400~3 450 m采用环空压力动态控制系统进行井底恒压控制钻进,钻井液密度为1.10 g/cm3,通过设定恒定井底ECD值,以微过平衡方式进行钻进,达到精确控制井底压力的目的。
计算所需基础数据为:井眼直径215.9 mm,钻井液密度 1.10 g/cm3,钻杆外径127 mm,排量10 L/s,起下钻速度0.3 m/s,2 350~3 500 m地层压力系数1.06~1.10,屈服值2.1 Pa,稠度系数0.679 51 Pa·sn,流性指数0.655 09。计算结果如表 1所示。
| 工 况 | 计算值 | 实际值 |
| 正常钻进 | 2.42~3.94 | 2.1~4.5 |
| 起钻 | 4.62~6.61 | 4.5~6.5 |
| 下钻 | 2.68~3.86 | 0.0~4.0 |
| 接单根 | 3.88~5.58 | 3.2~5.0 |
由表 1可知,通过模型计算的井口回压与实际值之间的误差较小,由此验证了控压钻井井口回压计算模型的准确性,该模型满足现场施工要求。
6.2 井口回压影响参数分析根据控压钻井井口回压计算模型,对前面实例在井深3 000 m进行纯钻井液控压钻进,各工况下均保持井底压力基本恒定,得出不同工况下井口回压与排量、钻井液密度、起下钻速度以及起下钻时间的关系,如图 3~图 6所示。
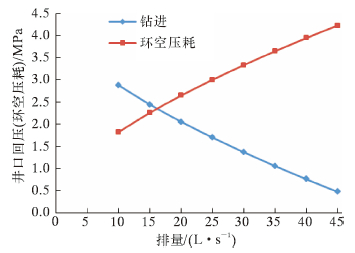
|
| 图 3 钻进时井口回压与排量的关系 Fig.3 The effect of displacement on the back pressure during drilling |
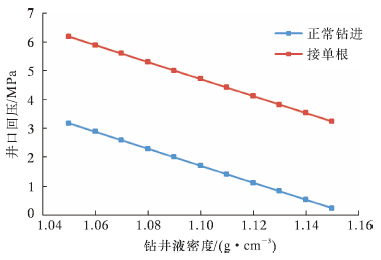
|
| 图 4 井口回压与钻井液密度的关系 Fig.4 The effect of mud weight on the back pressure |
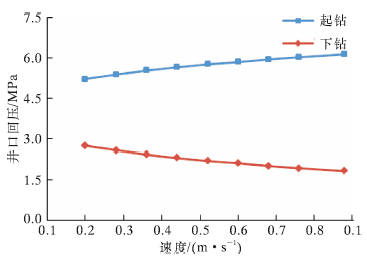
|
| 图 5 起下钻时井口回压与速度的关系 Fig.5 The effect of tripping speed on the back pressure during tripping |
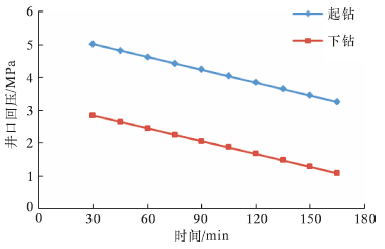
|
| 图 6 起下钻时井口回压与时间的关系 Fig.6 The effect of tripping time on the back pressure during tripping |
图 3是正常钻进时,保持井底ECD值为1.26 g/cm3时井口回压与排量的关系。从图可见,在满足正常井眼清洗所需排量的条件下,井口回压随排量的增大而减小。排量增大,井底压力随环空压耗增大而增大,故维持井底压力恒定所需的井口回压相应减小。
图 4是排量25 L/s、保持井底ECD为1.26 g/cm3时,钻进和接单根工况下井口回压与钻井液密度的关系。从图可见,接单根和钻进工况下井口回压都随钻井液密度的增大而减小。由于环空压耗远小于钻井液液柱压力,故井口回压与钻井液密度基本呈线性关系。
图 5是保持井底ECD值为1.26 g/cm3时,起下钻工况下井口回压与起下钻速度的关系。从图可见,井口回压随起钻速度增大而增大;下钻工况下,井口回压随下钻速度增大而减小。
图 6是起下钻速度为0.3 m/s,保持井底ECD值为1.26 g/cm3时,井口回压随起下钻时间的变化规律。从图可见,起下钻工况下的井口回压都随着起下钻时间的延长而减小。
7 结 论(1)基于控压钻井的工艺技术原理以及钻井工艺流程,将钻井过程划分为若干工况,根据流型+过程+工况的组合模式建立了控压钻井井口回压计算模型。
(2)基于圆管流量方程,以赫-巴流体流变模式为例,精确计算了系统环空压耗。结合稳态波动压力理论,推导赫-巴流变模式下的井下波动压力计算方程。通过实例对井口回压计算模型进行了验证,结果表明,计算误差较小,能满足现场施工要求。
(3)基于井口回压计算模型,对实例井进行模拟钻进,进一步分析不同钻井参数对井口回压的影响规律,得出了不同工况下井口回压与排量、钻井液密度、起下钻速度及时间的关系,这对控压钻井的安全实施具有重要的参考意义。
| [1] | 伊明,陈若铭,兰祖权,等.控压钻井系统研究[J].石油钻采工艺,2010,32(增刊1):69-72. |
| [2] | 周英操,崔猛,查永进.控压钻井技术探讨与展望[J].石油机械,2008,36(4):1-4. |
| [3] | 刘伟,蒋宏伟,周英操,等.控压钻井装备及技术研究进展[J].石油机械,2011,39(9):8-12. |
| [4] | 蒋宏伟,周英操,赵庆,等.控压钻井关键技术研究[J].石油矿场机械,2012,41(1):1-5. |
| [5] | Godhavn J M.Control requirements for high-end automatic MPD operations[C]//SPE/IADC Drilling Conference and Exhibition.Society of Petroleum Engineers,2009. |
| [6] | 余金海,孙宁,崔龙连.控压钻井环空水力模拟计算[J].石油钻采工艺,2011,33(4):1-5. |
| [7] | 杨雄文,周英操,方世良,等.控压钻井系统特性分析与关键工艺实现方法[J].石油机械,2011,39(10):39-44. |
| [8] | Farrow F D,Lowe G M.XXIII——The flow of starch through capillary tubes[J].Journal of the Textile Institute Transactions,1923,14(11):414-440. |
| [9] | Kelessidis V C,Maglione R,Tsamantaki C,et al.Optimal determination of rheological parameters for Herschel-bulkley drilling fluids and impact on pressure drop,velocity profiles and penetration rates during drilling[J].Journal of Petroleum Science and Engineering,2006,53(3):203-224. |
| [10] | 樊洪海,冯广庆,王果,等.一种新的流变模式及其应用性评价[J].中国石油大学学报:自然科学版,2010,34(5):89-93,99. |
| [11] | 周长虹,崔茂荣,黄雪静,等.钻井液常用流变模式及其优选方法[J].中国科技信息,2005(22):86-87. |
| [12] | 樊洪海.实用钻井流体力学[M].北京:石油工业出版社,2014. |
| [13] | Zhou Haobo,Fan Honghai.A new utility calculation model for axial flow of non-newtonian fluid in concentric annuli[J].The Canadian Journal of Chemical Engineering,2014,91(5):945-952. |
| [14] | 周开吉,杨金华,钟兵,等.井内波动压力[J].石油钻采工艺,1990(2):1-10. |
| [15] | 樊洪海,刘希圣.赫谢尔-巴尔克莱液体直井稳态波动压力计算模式[J].石油机械,1994,22(1):51-53. |
| [16] | 郭宇健,李根生,宋先知,等.基于四参数流变模式的钻井液稳态波动压力计算[J].钻采工艺,2014,37(5):1-4. |
| [17] | 汪海阁,苏义脑.管柱运动过程中钻井液粘附系数计算[J].钻采工艺,1996,19(6):64-66. |



