2. 中国石油集团钻井工程技术研究院;
3. 中国石油技术开发公司
2. CNPC Drilling Research Institute;
3. China Petroleum Technology & Development Corporation
0 引 言
目前连续管钻井(CTD)技术在国外已广泛应用于钻小井眼井、定向井、侧钻水平井以及欠平衡钻井等领域[1, 2]。CTD技术解决了许多常规钻井技术难以解决的问题,应用效果明显,在中国也有着广泛的应用前景[3, 4]。但连续管具有不可旋转性,因此在钻定向井或水平井时,必须依靠井下定向器调整工具面,从而控制井眼轨迹。这严重影响了CTD技术的应用与推广,为此,设计了连续管钻井电液定向器。相比液压定向器和电驱动定向器,它具有输出扭矩高、数据传输率高、连续双向旋转以及定向完成后可以锁紧工具面等优势。
1 技术分析 1.1 整体结构设计连续管钻井电液定向器结构如图 1所示,其总体结构设计包括动力机构、传动机构、锁紧装置和输出轴。

|
| 图 1 连续管钻井电液定向器结构示意图 Fig.1 Structural diagram of CTD electric-over-hydraulic orienter 1—电缆;2—微型电马达;3—行星齿轮机构;4—联轴器;5—空心驱动轴;6、8、10—轴向花键;7—锁紧套;9—复位弹簧;11—输出轴。 |
动力机构包括微型电马达,通过传动机构驱动空心驱动轴旋转;传动机构在电马达之下,自上而下包括行星齿轮机构、联轴器、万向节和空心驱动轴;锁紧装置在空心驱动轴下面,包括锁紧套和复位弹簧,在完成定向时能够锁紧工具面;输出轴在锁紧装置之下,输出轴的末端连接弯接头或弯马达,通过旋转工具面而起到定向作用。
1.2 工作原理钻井过程中,当钻头工具面角度达不到设计要求时,通过地面控制装置,加大地面泵泵压,钻井液经过连续管及其井下工具后进入定向器的液流通道,然后流经锁紧套,在压差的作用下,推动锁紧套下移,进入定向模式;同时,地面控制装置通过连续管内置的电缆向定向器中的电马达输送电能和控制信号,电马达根据控制指令可双向旋转,通过联轴器和万向节,经过减速机构驱动芯轴旋转;芯轴的末端与弯外壳相连接,以此达到调整工具面的目的,实现定向功能。当工具面调整到预期目标时,减小地面泵泵压到正常钻进数值范围,作用在锁紧套上的压差减小,在复位弹簧的作用下,推动锁紧套上移,进入锁紧模式,钻头将按照当前工具面角度持续定向钻进。当需要再次调整工具面角度时,重复“定向模式”与“锁紧模式”操作即可。
1.3 主要技术参数初步设计定向器总长4 m,外径85.7 mm,最大扭矩1 kN·m,定向精度±2.5°,工具面定向范围-200°~+200°,旋转速度1.0°~1.5°/s。
2 定向及锁紧的排量范围计算钻井液流经锁紧套,经过锁紧套的上部突缩断面、中央细钻井液通道以及下端突扩断面的节流与阻流作用,在锁紧套的上、下端面产生压降。增大排量,使液流压差产生的正压力足以克服弹簧的反作用力,推动锁紧套下移,进入定向模式;减小排量,液流产生的压降不足以克服弹簧的反作用力,锁紧套在弹簧的作用下复位,进入锁紧模式。因此,需要选择定向与锁紧时合适的钻井液排量。
2.1 确定CTD钻井排量范围井壁稳定条件下钻井液最大环空返速为[5]:
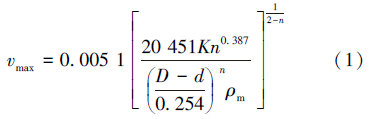
钻井液携岩所需最低环空返速为:
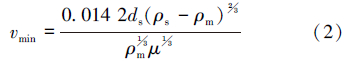
由井壁稳定确定的最大和最小环空流量为:
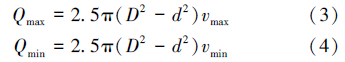
当D=114.3 mm,d=73.0 mm,ρm=1.1 g/cm3,ρs=2.5 g/cm3,根据现场经验,vmin一般取1.0 m/s,同时根据螺杆钻具的技术参数得出本例中CTD的排量范围为6.0~10.9 L/s。
2.2 物理模型电液定向器锁紧套轴向受力分析如图 2所示。定向器锁紧套上、下移动所受合力是a环面压力Fa、b环面压力Fb、弹簧反作用力Fn和自身重力G的函数,表达式为:
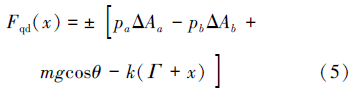
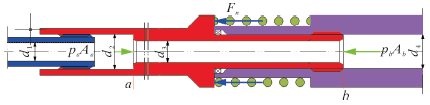
|
| 图 2 锁紧套轴向受力分析 Fig.2 Diagram of axial forces on the locking sleeve |
定向器外径85.7 mm,定向及锁紧有关的其余结构参数如图 2所示,d1=17.3 mm,d2=33.0 mm,d3=15.0 mm,d4=32.0 mm。为了减小液流对锁紧套的冲击,对上、下端面进行了倒角,并进行了角度优化(见图 3)[6]。倒角计算式为:
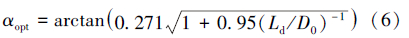
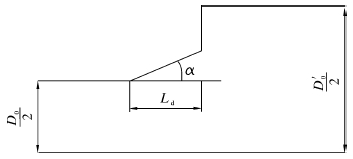
|
| 图 3 倒角优化示意图 Fig.3 Schematic diagram of bevel edge |
为了使流体充分发展,取断面变化前距离为5倍管径,变化后距离为8倍管径,流体计算域见图 4。假设流过定向器锁紧套的流体为稳态、不可压缩、单相紊流,且为牛顿流体。对流体进行三维数值分析,列出相关的连续性方程以及动量方程[7, 8, 9, 10]:
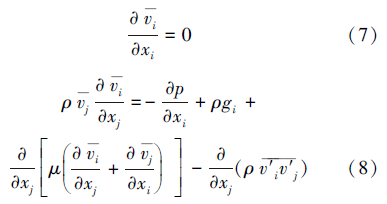
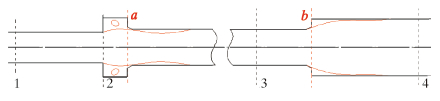
|
| 图 4 流体计算域示意图 Fig.4 Schematic diagram of computational domain for fluids |
在笛卡尔坐标系中求解上述方程,其中,xi=(x,y,z),gi=(0,0,-g),假设水平放置。
根据Boussinesq涡粘假定,得出Reynolds应力相对于平均速度梯度的关系为:
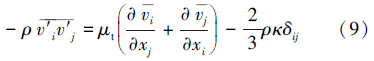
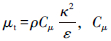 为经验常数,ε为耗散率。
为经验常数,ε为耗散率。
将式(9)带入式(8),得到综合形式的RANS方程:
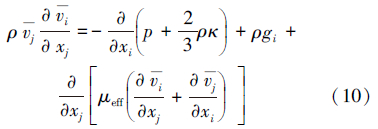
κ-ε模型计算量适中且精度和适用性好,是目前工程中最常用的湍流模型,采用标准κ-ε模型确定κ、ε,相应的输运方程为:
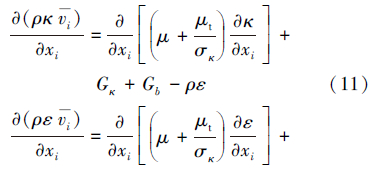
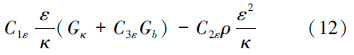
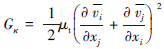 ;Gb为由浮力引起的湍动能κ的产生项,
;Gb为由浮力引起的湍动能κ的产生项,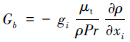 ;Pr为湍动Prandtl数,该模型中取0.85;
;Pr为湍动Prandtl数,该模型中取0.85;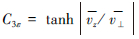 ,
,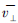 为垂直于重力加速度的平均速度分量;公式中的经验数值C1ε=1.44,C2ε=1.92;Cμ=0.09;Cκ=1.0;Cε=1.3。
为垂直于重力加速度的平均速度分量;公式中的经验数值C1ε=1.44,C2ε=1.92;Cμ=0.09;Cκ=1.0;Cε=1.3。
边界条件:流体以一定速度在管道中流动,内部介质为温度90 ℃的钻井液,密度1 100 kg/m3,动力黏度0.08 mPa·s。为了使进、出口和突扩、突缩截面的流动充分发展,进口采用速度入口,并给定入口流速;κ和ε值根据经验公式得κin=0.003 75v2in,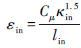 ,其中lin=0.5D,D为进口当量直径。出水口为压力出口,各速度分量、κ和ε均取为第2类边界条件,即
,其中lin=0.5D,D为进口当量直径。出水口为压力出口,各速度分量、κ和ε均取为第2类边界条件,即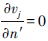 (j=1,2,3);
(j=1,2,3);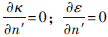 ,n′为出口断面的单位法向量。固壁边界采用无滑移条件,近壁区采用标准壁面函数法。
,n′为出口断面的单位法向量。固壁边界采用无滑移条件,近壁区采用标准壁面函数法。
在对网格进行划分时,本着对重点部位进行加密,一般部位适当放宽的原则。在突扩和突缩界面及附近区域,网格密度较大,网格尺寸很小,约0.3 mm,边壁处理为壁面函数法。采用有限体积法(Finite Volume Method)将以上方程转化为代数方程组。为保证计算精度,采用2阶迎风格式,隐式求解,速度和压力方程采用Simplec算法耦合。采用小残差收敛标准,增加迭代的次数。
2.4 压力差理论基础利用能量方程,考虑局部损失及沿程损失,得到上、下2端面的压力理论表达式[6]。
a断面压力为:
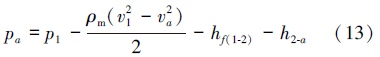
b断面压力为:
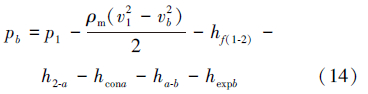
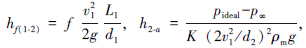
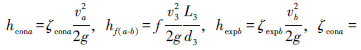
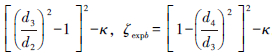 。
。
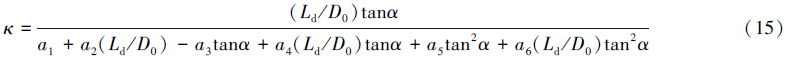
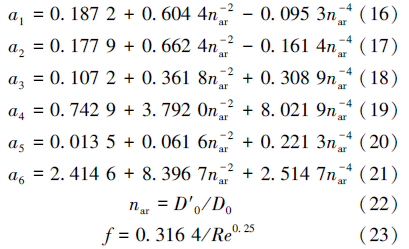
模拟参数:入口流量Q=6~10 L/s,垂深1 000 m,井底温度90 ℃,管壁表面粗糙度0.01 mm。以入口流量7 L/s为例,得到锁紧套上、下端面(a、b断面)以及充分发展区(4断面)的压力分布云图,如图 5所示。
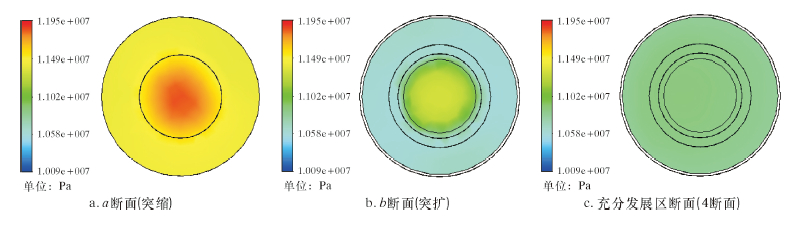
|
| 图 5 a、b端面及充分发展区的压力分布云图 Fig.5 Cloud charts for distribution of pressures on a & b ends and fully developed zones |
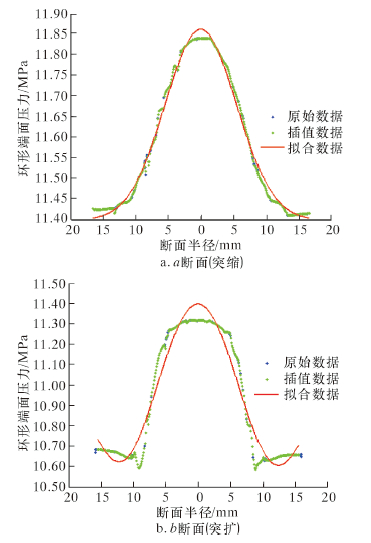
Bernoulli方程通常简单地假设环形端面的压力等于充分发展区的压力,例如pb≈p4,但从图 5和表 1可以看出,两者存在较大的差别,且随着流量增大,两者差别有增大的趋势。因此,笔者直接对环形端面压力进行了数值拟合(见图 6),对前、后两端面的压力差进行了更加精确的求解。
| Q/(L·s-1) | 6 | 7 | 8 | 9 | 10 |
| pb/kPa | 10 703 | 10 673 | 10 635 | 10 593 | 10 531 |
| p4/kPa | 10 832 | 10 843 | 10 857 | 10 872 | 10 889 |
| p4-p6/kPa | 129 | 170 | 222 | 279 | 359 |
|
| 图 6 径向压力拟合分布 Fig.6 Total pressure fitting curve along radial direction |
得到a、b断面压力拟合函数为:
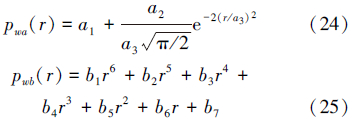
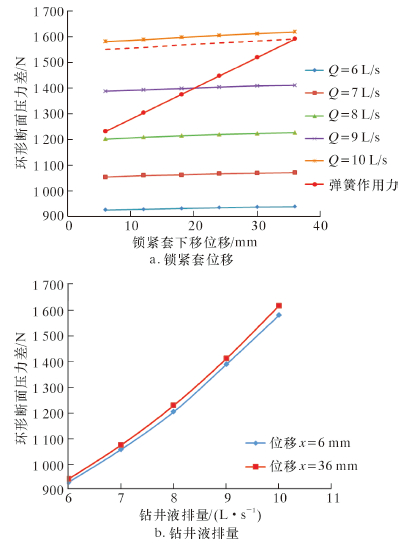
按照上述数值计算方法,根据式(26)~(28)得出锁紧套上、下端面在不同流量下所受的压力差,如图 7所示。
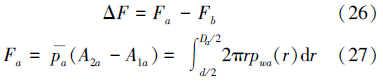
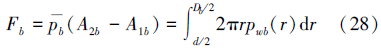
|
| 图 7 a、b环形端面压力差随流量变化示意图 Fig.7 Variation of differential pressures with flow rates at a & b ends |
结合定向器及锁紧套的径向尺寸,根据GB/T 2089—2009选定复位弹簧参数,弹簧参数如下。
材料直径8 mm,弹簧中径60 mm,最大工作载荷1 835 N,最大心轴直径47 mm,最小套筒直径73 mm,自由高度260 mm,最大工作变形量142 mm,弹簧刚度12 N/mm。
从流量变化产生的压力差以及复位弹簧对锁紧套的作用力的模拟结果来看,可得如下结论。
(1)流量一定时,随着锁紧套的下移,a、b环形端面压力差有为微弱增加的趋势;反之,随着锁紧套的上移,a、b环形端面压力差有为微弱减小的趋势。
(2)随着排量增加,a、b环形端面压力差有明显增大的趋势,且在同一位置处,随着排量增大,压力差以抛物线趋势增大,排量从6~10 L/s每增加1 L/s,a、b环形端面压力差的增大值从128.6 N增大到207.5 N;反之,随着排量减小,呈现相反的结果。
(3)锁紧套下移过程中,弹簧被压缩,根据胡克定律,其反作用力随着锁着套下移呈线性增大,如图 7a所示,当钻井液排量超过9.75 L/s时,液流通过锁紧套产生的正压力能够完全克服弹簧的反作用力,使锁紧套的上端花键与心轴末端花键能够完全配合,进入定向模式;锁紧套上移过程中,当钻井液排量低于8.25 L/s时,弹簧的反作用力大于锁紧套前后端面的压力差,锁紧套上移,使锁紧套外侧花键与套筒内侧花键完全配合,进入锁紧模式。
(4)结合2.1中CTD的排量范围,得出定向器定向过程中所需最佳排量范围为9.75~10.90 L/s;定向器锁紧过程中所需最佳排量范围为6.00~8.25 L/s,也即正常钻进的排量范围。
3 电液定向器的技术优势相对于液压定向器和电驱动定向器,电液定向器有如下优点[11]:①电液定向器采用电马达驱动旋转定向,而且利用电缆传输数据,效率高。②电液定向器可以连续双向旋转定向,调整速度一般在0.5°~1.5°/s,“点击式”的钻进可以消除定向段的“鱼尾”现象,利于CT的延伸。③相比于电驱动及液压驱动定向器,电液定向器可以利用压差通过锁紧套将弯外壳固定在预定工具面,即将钻头工具面角度“锁紧”,实现工具面的精确摆放。
4 结 论(1)电液定向器通过地面控制装置控制钻井液压力及排量的大小来改变锁紧套的位置,从而实现定向器在定向模式与锁紧模式之间的转换。
(2)对不同排量下锁紧套前、后2端面压力差的数值模拟分析结果表明,定向过程中的最佳排量为范围为9.75~10.90 L/s,锁紧过程中所需最佳排量范围为6.00~8.25 L/s。
(3)相比于传统的液压定向器,电液定向器具有连续双向旋转、效率高、精度高、可靠性强等特点;相比于电驱动定向器,电液定向器能够在达到预期工具面角度后克服反扭矩的影响,锁紧工具面,实现工具面的精确摆放。
| [1] | 贺会群.连续油管技术与设备发展综述[J].石油机械,2006,34(1):1-6. |
| [2] | 贺会群.连续管钻井技术与装备[J].石油机械,2009,37(7):1-6. |
| [3] | 侯学军,高德利,沈忠厚.微小井眼电机驱动CT牵引器控制系统设计[J].石油机械,2013,41(3):40-45. |
| [4] | 侯学军,高德利,沈忠厚.微小井眼连续油管钻井牵引器系统结构设计[J].石油钻采工艺,2013,35(2):1-5. |
| [5] | 周昆.连续油管钻井老井加深工艺技术研究[D].武汉:长江大学,2013. |
| [6] | Bae Y,Kim Y I.Prediction of local pressure drop for turbulent flow in axisymmetric sudden expansions with chamfered edge[J].IChemE,2014,92:229-239. |
| [7] | Zambrano H,Sigalotti L D G,Pea-Polo F.Turbulent models of oil flow in a circular pipe with sudden enlargement[J].Appl.Math.Modell.,2015(2):481-496. |
| [8] | Pinho F T,Oliveira P J,Miranda J P.Pressure losses in the laminar flow of shear-thinning power-law fluids across a sudden axisymmetric expansion[J].Heat and Fluid Flow,2003,24:747-761. |
| [9] | Kaushik V V R,Ghosh S,Das G.CFD simulation of core annular flow through sudden contraction and expansion[J].Petroleum Science and Engineering,2012,86/87:153-164. |
| [10] | Javadi A,Nilsson H.LES and DES of strongly swirling turbulent flow through a suddenly expanding circular pipe[J].Computers & Fluids,2015,107:301-313. |
| [11] | Burke J,Eller G,Venhaus D,et al.Coiled tubing drilling:Increasing horizontal reach in the Kuparuk field[R].SPE168250,2014. |



